桥梁结构健康监测基于相关性分析的多源数据预测算法研究

薛国华 李明慧 韩宇轩 杨柳 刘恒

1.国家能源集团国际工程咨询有限公司，北京 100007；2.西南交通大学信息科学与技术学院，成都 611756；3.综合交通大数据应用技术国家工程实验室，成都 611756；4.中国电子科技集团第十研究所，成都 610036

国家能源集团自1989年开通运营第一条铁路以来，发展至今所拥有的自有铁路总里程达2 400 km，以重载铁路为主，常态化开行两万吨列车。桥梁结构是铁路安全运营的基础，沿线铁路桥梁构成串联系统，任一跨桥梁失效都将导致线路中断。

国能集团管辖的铁路桥梁结构形式多样，桥梁上下部主体结构及附属设备随着运营年限及运量增长而逐渐老化，运营性能和安全性指标逐渐下降。为了对桥梁结构损伤进行评估，需要监测桥梁运行的各项参数，综合评估桥梁使用状况。

桥梁作为一个整体将受到环境变化、荷载或其他设备等因素的共同影响。当铁路桥梁某类数据受到外部影响产生变化时，其他桥梁监测类型的数据也会同样受到这种外部影响产生相应的变化。因此，虽然线路中的铁路桥梁组成结构复杂、边界条件模糊、监测系统布设的监测点数量不足，但还是可以通过这种关系利用不同监测数据类型之间相互验证的方法，来间接对铁路桥梁多项监测参数进行验证。使用机器学习模型进行这种验证分析能为铁路桥梁设备维护提供新的技术手段［1］。

韩宇等［2］针对传统桥梁结构损伤诊断方法在时间联合序列信号特征提取及损伤识别方面不理想的问题，通过卷积神经网络对动挠度、动应变进行传感器拓扑相关特征提取后，再利用LSTM网络进一步提取时间维度相关性特征，实现了特定工况下桥梁损伤的识别。邓思勉［3］结合传感器信息融合的相关理论对桥梁监测数据异常进行研究，在特征级融合中，选取灰色关联度这个表征各个传感器之间数据相关性的指标；在决策级融合中，通过特征级融合中对灰色关联度的分析总结出了数据异常原因是传感器故障的判据。刘扬等［4］为实现钢-混组合桥面系空间温度场与温度效应实时评估与预测，构建包含“结构特征、时间特征、环境特征”映射的样本库，提出BP-LSTM混合模型的空间温度场及温度效应评估及预测方法，并通过实测数据验证有限元计算的准确性。包云等［5］结合高速铁路风监测数据，建立高速铁路大风危险性评估指标，提出大风危险性评估方法，为高速铁路气象灾害的精细化监测和防御提供借鉴。

对多类型桥梁监测数据进行相关性分析，能有效防止因某种监测数据出现异常而对桥梁整体安全状况产生误判。这将增加桥梁监测数据的容错率，并为桥梁病害预测提供有力的数据支撑。

1 数据集说明

桥梁健康监测数据是一种基于时序的不断变化的数据，环境变化、人类生产活动都会对其造成较为严重的干扰［6］。国能集团管辖的某铁路部分桥跨采用了钢混结合梁和预应力混凝土低高度梁结构，因现行的TG/GW 103—2018《普速铁路桥隧建筑物修理规则》与铁运函〔2014〕《铁路桥梁检定规范》中缺少对其检查、检测的相应标准，需要研究对其进行长期在线监测的方案。

通过对某座铁路桥梁进行结构健康监测得到监测数据集。数据类型包括位移（mm）、应变（MPa）、风速（m/s）、温度（°C）、湿度（%）和索力（kN）。监测时间自2021年1月2日至29日，数据采集时间间隔为1 h。

2 数据相关性分析及Bi-LSTM模型预测

2.1 基于傅里叶变换的桥梁监测数据相关性分析

傅里叶变换可以将时域的信号变换到频域的正弦信号，从而呈现数据的频谱特征，获取数据的频率组分［7］。首先利用快速傅里叶变换（Fast Fourier Transform，FFT）得到桥梁健康监测数据归一化频谱，接着比较频谱的分布规律，进而分析不同监测数据之间的相关性。

首先，对位移监测数据进行FFT变换，图1（a）为其归一化频率振幅图，有一个主要频率，在零点附近。接着，对温度、应变、风速、湿度和索力监测数据进行FFT变换。频谱如图1（b）—图1（f）所示。

图1 各类监测数据的频谱

由图1可知，温度、应变、风速、温度4种数据类型具有较为相似的3个频率分量，分别出现在频率0、0.05、-0.05的位置，且这3个频率点的幅值大于其他点，特别是零点对应的幅值远远大于其他点的幅值。这4种数据类型的归一化频谱图，高幅值的频率对应的频率点保持高度一致，具有不同程度的相关性。

2.2 基于小波变换的桥梁监测数据相关性分析

小波变换是一种时间和频率的局域变换方法，可以将数据分解为不同的时间尺度，从而获取不同频率下的信号成分，提取有用信息［8］。

对桥梁位移信号进行4层小波分解，见图2。

图2 位移小波分解

图2从上往下分别是位移小波细节层分解信号d1、d2、d3和d4。d1层与d2层含有较多噪声信号，经过小波变换后的d4层信号可以有效地排除桥面活载的影响。

选取位移、温度小波分解后的d4层信号进行对比，验证位移与温度数据之间的相关性。图3为位移-温度信号小波分解d4层对比图。可以看出，位移与温度信号具有高度相似的变化趋势：位移信号变大，温度信号变小；位移信号变小，温度信号变大，且变化幅度高度一致。由此推测，位移信号与温度信号具有负相关性。

图3 位移-温度小波分解d4层对比

接下来，对温度、应变、风速、湿度和索力信号进行4层小波分解，如图4所示。监测数据会受到季节变化和人类活动等因素的影响。使用小波细节层信号d4来比较信号之间的相关性。图5分别是应变-温度、索力-温度、位移-湿度和位移-风速信号小波分解d4层的对比图。d4层受到外部影响较小，信号在d4层的变化可以真实反映信号之间的相关性。图5（a）、图5（b）中小波分解信号相关性不显著。图5（c）中的d4层位移和湿度信号具有正相关性，即随着位移信号增大，湿度信号会增大；位移信号减小，湿度信号会减小。图5（d）中位移信号与风速信号存在负相关性，即随着位移信号增大，风速信号会减小；位移信号减小，风速信号会增大。

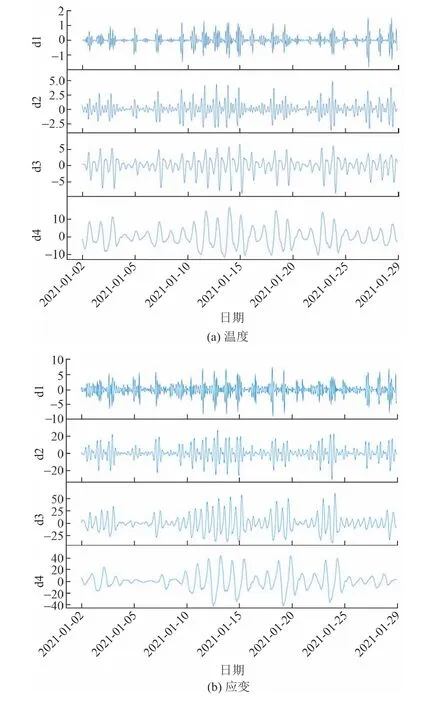
图4 各参数小波分解

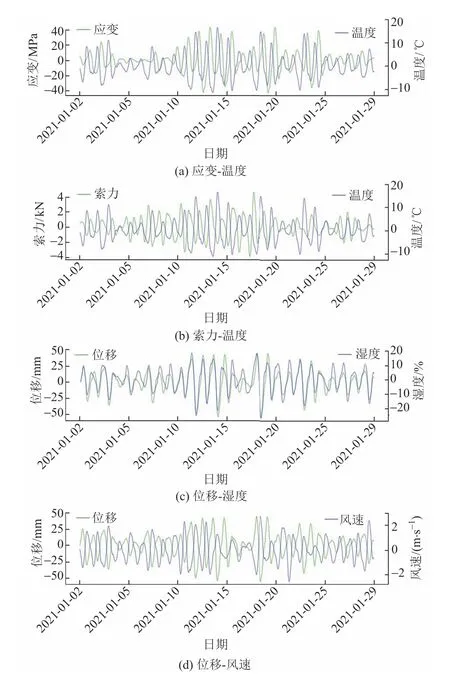
图5 两参数小波分解d4层对比

相关系数是用以反映变量之间相关关系紧密程度的统计指标［9］。皮尔逊相关系数绝对值计算公式（1），其值在［0，1］，越接近1表示二者相关性越高。

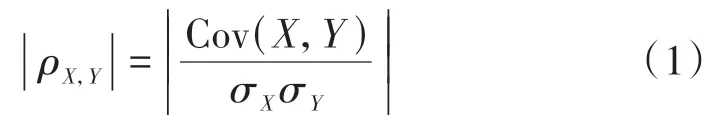
式中：Cov(X，Y)表示X、Y之间的协方差；σX、σY分别表示X、Y的标准差。

根据小波分析相关性结果，分别计算小波d4层分解位移信号与小波d4层分解温度信号、湿度信号和风速信号的相关系数，结果见表1。通常情况下通过表2判断变量间的相关程度。

表1 相关性系数计算

根据计算结果，选取与位移信号具有极强相关性的温度和湿度信号来建立多源预测模型，进一步证明数据之间的相关性。

表2 相关性判定

2.3 基于相关性分析的桥梁结构健康监测多源数据预测

长 短 期 记 忆（long short term memory network，LSTM）［10］神经网络是在传统循环神经网络（recurrent neural network，RNN）基础上改进的深度学习网络。LSTM神经网络在RNN结构上引入一个新的状态单元Ct，解决RNN梯度爆炸或梯度消失导致的长期依赖问题。

LSTM单元由一个记忆单元和输入门（update gate）、输出门（output gate）和遗忘门（forget gate）三个门构成。记忆单元的作用是对信息进行管理和保存，三个门的作用是控制记忆单元中信息的更新、衰减、输入、输出等动作。它的主要思想是通过学习LSTM单元中三个门的参数来管理记忆单元中的信息，从而使有用的信息经过较长的序列也能保存在记忆单元中，在处理较长时间序列数据时表现良好。其单元结构如图6所示。

图6 LSTM模型

LSTM单元在t时刻的输入由输入层xt、序列中前一个单元的隐含层ht-1和记忆单元Ct-1三部分构成，在t时刻的输出为该单元的隐含层ht和记忆单元Ct。首先通过计算三个门的信息输出，来控制记忆单元的信息，然后计算记忆单元内的信息，最后使用记忆单元值和输出门计算该时刻隐含层的值。各单元内部更新过程参见文献［11］。

通常，LSTM网络中的信息是单向传输，只能使用过去的信息，而不能使用将来的信息。为了适应桥梁监测数据变化特性，最终选取双向长短期记忆（bidirectional long short-termmemory，Bi-LSTM）［12］神经网络用于构建多源预测模型。Bi-LSTM由正、反向LSTM结合形成，增加了从后向前的计算过程，可以考虑数据间的前后关联。前向LSTM可以获取输入序列的过去数据信息，后向LSTM可以获取输入序列的未来数据信息，对时间序列实现向前和向后两次LSTM训练，可以进一步提高特征提取的全局性和完整性，其结构如图7所示。

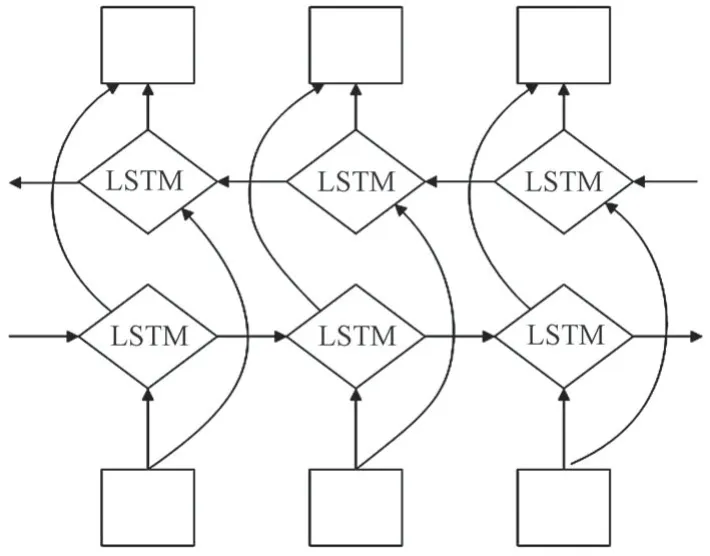
图7 Bi-LSTM结构

根据2.2节中推测的结论：位移与温度数据之间具有负相关性，位移与湿度数据之间具有正相关性。使用温度与湿度数据作为模型输入，建立Bi-LSTM多源预测模型，进一步分析、证明数据之间的相关性。

为了测试Bi-LSTM的预测效果，通过以下2个试验进行验证：Bi-LSTM与LSTM预测对比实验、基于数据相关性的Bi-LSTM预测模型试验。试验目的如下：①对比Bi-LSTM与LSTM的性能。②评价基于数据相关性的Bi-LSTM多源预测模型的能力。

选取3个性能指标以评估各类模型的预测效果，包括平均绝对百分误差（mean absolute percentage error，MAPE）、平均绝对比例误差（mean absolute error，MAE）、均方根误差（root mean square error，RMSE）。各评价指标定义如下：

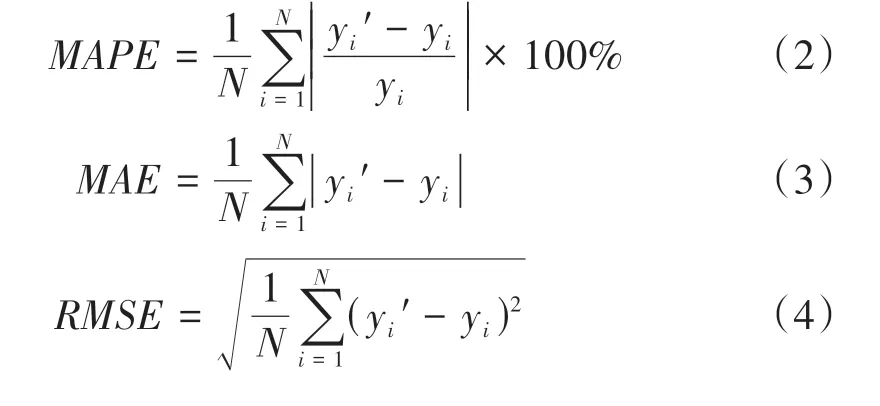
式中：yi为真实值，yi'为预测值，N为样本个数。

性能指标值越小，表明建立的模型精度越高。

2.3.1 Bi-LSTM与LSTM预测对比试验

采用位移监测数据，分别利用LSTM和Bi-LSTM模型进行预测，并对比2种方法所预测生成的曲线的准确度。模型含有2个记忆层，其中隐藏单元个数是50，最后接有一个全连接层，用来输出结果。LSTM模型和Bi-LSTM模型对位移数据的预测结果如图8所示。

图8 模型对位移的预测

从图8（a）可以看出，LSTM模型的预测值与真实值存在较大误差。

从图8（b）可以看出，Bi-LSTM的整体预测结果比LSTM模型更加接近真实值，能反映位移的真实变化情况。

LSTM和Bi-LSTM 2种模型预测误差值见表3。可见，Bi-LSTM模型比LSTM模型预测精度有提高，预测结果更加具有可信度，在位移预测方面Bi-LSTM模型更加实用和有效。

表3 LSTM与Bi-LSTM模型预测误差对比

2.3.2 基于数据相关性的Bi-LSTM多源预测模型

基于相关性分析推论，融合温度和湿度因子作为训练数据，输入基于数据相关性的Bi-LSTM模型，通过训练好的模型验证位移数据的预测准确度，并与未考虑数据相关性的Bi-LSTM模型作对比。采用的Bi-LSTM模型中包含多个全连接层，使用LeakyReLU激活函数，避免ReLU可能出现的神经元“死亡”现象，最后接有一个全连接层，用来输出结果。Bi-LSTM模型预测结果见图9。

从图9（a）可以看出，仅用位移数据作为模型的输入时，预测结果能描述曲线的大概走向，但是测试值与真实值存在一定的差距。

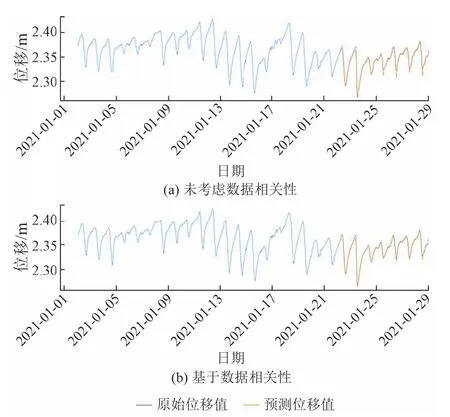
图9 Bi-LSTM模型对位移的预测

从图9（b）可以看出，基于数据相关性的Bi-LSTM模型预测的位移变化趋势更贴近真实数据，说明了融合温度和湿度数据的位移预测模型的优越性。其拟合精度更高，预测效果更好，误差更低，进一步证明了对桥梁监测数据进行相关性分析的必要性和正确性。

Bi-LSTM两种模型位移预测误差对比见表4。可知，特征关联性分析能够使预测模型具有良好的预测效果，有效地获取并利用强关联外界影响因素来预测位移数据具有实际意义。

表4 Bi-LSTM两种模型位移预测误差对比

3 结论

本文基于桥梁健康监测数据，首先使用傅里叶变换分析了信号之间的频率幅值关系，接着通过小波变换分析不同监测数据类型之间的相关性，最后建立了基于数据相关性的Bi-LSTM多源预测模型，试验结果说明了建立的预测模型的优越性。

主要结论如下：

1）桥梁监测数据在零点有主要的频率分量，在零点附近有2个次要的频率分量，说明桥梁监测数据中不同类型信号在一定程度上具有关联性。

2）桥梁监测数据经4层小波变换后，d4层受到的外部干扰最小，通过对比d4层小波细节层信号发现位移信号与温度信号具有负相关性、与湿度信号具有正相关性。

3）建立了基于数据相关性的Bi-LSTM位移预测模型，模型融合与位移数据具有强相关性的温度和湿度数据，并与未考虑数据相关性的Bi-LSTM预测模型进行对比。试验结果说明了融合数据相关性的Bi-LSTM预测模型的优越性，证明桥梁的位移数据和温度数据具有负相关性，位移数据与湿度数据具有正相关性的结论是正确的。利用桥梁健康监测数据进行数据处理和挖掘具有重要的工程应用价值。

基于相关性分析的多源数据预测模型能够弥补单一数据预测模型的局限性，对于保障桥梁结构状态、实施长期监测和实时预测预警具有重要的理论意义和工程价值。