基于可拓物元模型的在役斜拉桥安全性能评估

胡永杰、戴新荣、厉万众

（温州市交通发展集团有限公司，浙江温州 325000）

0 引言

随着我国交通运输事业的发展，桥梁作为交通枢纽，也取得了较快的发展。然而，由于结构自身、外部环境以及管养不足等影响，随时间推移，桥梁性能总会不可避免地发生退化，从而导致构件失效、承载能力降低，严重时甚至导致整座桥梁的倒塌，造成巨大的人员伤亡和经济损失。

为了减少事故的发生，实时掌握在役桥梁的健康状况，保证桥梁能达到预期的使用寿命，从经济和社会发展的角度而言，必须在桥梁的整个寿命周期内科学地对桥梁进行监测和评估。

既有桥梁的健康状态评估主要是依据人工检查信息，由于养护人员专业水平参差不齐等，容易导致检测结果粗糙、主观性强[1]，且检测时间周期较长，难以客观真实地反应桥梁安全状况，无法及时进行桥梁评估并制定养护计划。

随着传感器技术的不断发展，越来越多的桥梁安装了健康监测系统。通过传感器对特定的物理量进行长期监测，得出的数据指标是桥梁运营过程中特定状态的真实反映。基于对海量监测数据进行分析，可以实时了解桥梁的健康状况，为桥梁养护决策提供数据支撑。

常用的桥梁安全性能评估方法包括综合评估法、层次分析法以及模糊综合评估法等，这些方法虽然能在一定程度上评估桥梁结果，但仍存在许多问题。由于桥梁评估过程复杂，指标类型多样，传统的评估方法，难以解决指标间相互矛盾以及定向、定量信息共存的问题，且多是针对单一指标进行评估，难以真实反映桥梁的健康状况。而可拓评估法是通过建立物元模型，确定待评对象的经典域和节域，通过计算各评价指标的权重以及关联度来确定最终综合等级的方法，从定性和定量两个角度处理矛盾问题，探索事物的本质，并作定量分析。部分学者已将可拓理论引入桥梁评估中，如王琳[2]基于可拓理论建立了桥梁的可靠性评价模型，为桥梁病害防治与维修加固提供参考和理论依据。

刘芳平[3]基于可拓理论，利用关联函数和可拓算法对评估指标进行计算，实现对桥梁的综合评估，但以往研究都基于桥梁的检测数据。基于此，本文以桥梁监测数据为基础，引入可拓理论，通过关联函数建立评定指标与等级之间的联系，以实现对桥梁的综合评估。

1 基于可拓理论的桥梁评估

可拓学是蔡文等教授创立的一门新学科[4]，以物元理论为基础，目的是解决事物间矛盾相容、定性定量共存的问题，基于可拓理论对斜拉桥安全性能评估的流程如下：

1.1 确定待评物元、经典域和节域

1.1.1 待评物元

式（1）中：P0表示待评斜拉桥的安全性能；ci表示第i个评估指标；vi表示第i个评估指标实际值。

1.1.2 经典域

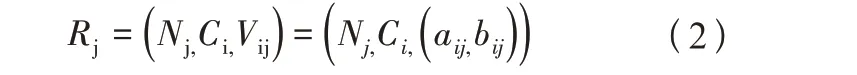
式（2）中：Nj表示 斜 拉 桥 安 全 性 能 评 估 的 第j(j=1,2,…,m)个 等 级；Vij=(aip,bip)表示安全性能评估属于第j个等级时ci对应的取值范围，即经典域。

1.1.3 节域

式（3）中：P表示斜拉桥安全性能评估等级的全体；Vip=(aip,bip)表示评估指标ci的所有取值范围，即节域。

1.2 确定各个评估指标的关联函数值

基于关联函数，可得实测值与状态等级区间之间的关联度为：

1.3 确定权重

熵权法是根据评价指标变异程度的大小来确定指标权重，采用熵权法确定各指标权重不依赖专家经验，能够有效减少主观性[5]，流程如下：

1.4 确定多指标关联度

待评对象P0关于等级j的关联度为：

1.5 综合等级评定

2 基于监测数据的可拓评估方法研究

由于监测数据类型多样，因此采用指标的相对变化量α来反映桥梁的健康程度。首先可将各类监测指标数据看作一个总体，由于各样本点数据相互独立，可近似认为总体服从正态分布；其次由于样本数量很大，可进一步认为其服从标准正态分布，基于数理统计，将偏离程度利用置信区间进行定量划分。

根据交通运输部对多座桥梁的统计分析，并结合相关标准中对桥梁状态等级的划分，可认为5 种桥梁状态等级发生的概率分别为0.2、0.6、0.15、0.04、0.01。对于标准正态分布，当置信度为1 时，正置信区间为[0,3.09]，即节域为[0,3.09]。由此可得出当评定等级分别为1～5 时，α 的范围分别为（0,0.26]、（0.26,1.29]、(1.29,1.96]、(1.96,2.33]、(2.33,3.09]，即经典域的各区间范围。与之相应的桥梁评分分别为[100,95）、[95,80）、[80,60）、[60,40)、[40,0），具体的桥梁评分值大小，可根据α 的数值进行线性内插得到。

3 实例分析

3.1 工程概况

某斜拉桥为双塔双索面叠合梁斜拉桥，跨径布置为（50+110+380+110+50）=700m，采用五跨连续半漂浮体系，空间密索型布置，索塔为“A”型塔身，下部结构采用墙式墩，桥梁宽33.0m，双向六车道。为实时监测和评估桥梁结构的性能状况，基于该斜拉桥运营条件以及结构危险性分析，并结合相应的监测规范，对该桥布置了相应的健康监测系统，以用于运营环境及荷载监测和结构响应监测。

3.2 建立该斜拉桥评定指标体系

根据监测数据类型，结合该桥实际情况，建立该桥合理的评定指标体系，如图1 所示。

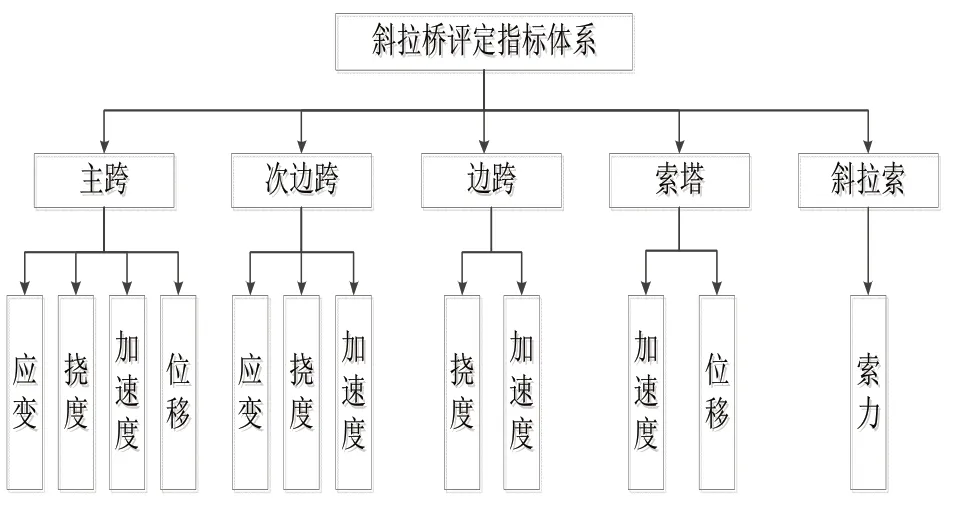
图1 该斜拉桥评定指标体系

3.3 监测数据处理

选取该大桥某一时间段的监测数据进行分析，首先对数据进行预处理，为避免交通荷载等影响，选取一天中0 时到1 时数据中的最大值作为代表值进行计算，以主跨的挠度监测数据为例，结果见表1。

表1 主跨截面1#测点监测值

基于表1 可得，α的取值范围为( )0.0268,2.2213 ，均值为0.8354。主跨共布置14 个挠度测点，同理，可计算主跨其他13 个挠度测点的α值以及各测点的评分，进一步计算可得该斜拉桥主跨挠度各测点的综合得分为88.46 分，各测点状态等级均为2 级。同理可求得该斜拉桥其他部件各监测指标的α均值分别为0.8365、0.8452、0.8596、0.8588、0.8210、0.8412、0.8102、0.8352、0.8056、0.8463、0.8512、0.8485，可得部件各监测指标的状态等级均为2 级。

3.4 指标权重计算

为克服采用传统层次分析法确定权重导致主观性强、指标真实状态值利用率低等问题，本文基于该斜拉桥海量的监测数据，采用熵权法确定各级指标权重 ，计 算 得 各 一 级 指 标 权 重 分 别 为ωi=(0.3325,0.1163,0.0925,0.2031,0.2556 )，二级指标权重为ω11=( 0.2024,0.2431,0.3011,0.2534 ),ω12=( 0.2812,0.3315,0.3873),ω13=( 0.4856,0.5144 ),ω14=(0.4758,0.5242 ),ω15= 1。

3.5 斜拉桥整体评估

利用公式（7）计算斜拉桥安全性能等级的关联度为：

4 结语

为实时掌握在役桥梁的健康状况，本文以温州市某斜拉桥为工程背景，基于海量的监测数据进行斜拉桥健康状况评估。首先基于监测数据分析建立了该斜拉桥的监测评定指标体系，以监测数据相对变化量为基准，将桥梁等级评分与正态分布置信区间联系起来，然后引入可拓物元模型并结合熵权法对监测数据进行处理，按照“测点—部件—全桥”的顺序依次计算桥梁的等级及评分，结果表明该桥梁各部件以及桥梁整体均处于2 级，桥梁状态良好，处于安全可控状态。本文基于监测数据对桥梁进行评估的方法，简单易行，结果合理，可为同类桥梁的性能监测评估提供参考。