用常规思维解决非常规问题
2023-01-09卢红卫
卢红卫
(江苏省张家港市外国语学校 215600)
2021年全国高中数学联合竞赛一试第7题看似形式复杂,实则用简洁的常规思路即可解决.
题目a1,a2,…,a21为1,2,…,21的排列,满足|a20-a21|≥|a19-a21|≥|a18-a21|≥…≥|a1-a21|,这样的排列的个数为.
思路1 特殊开路,归纳猜想.
a1,a2,…,a5为1,2,…,5的排列,满足|a4-a5|≥|a3-a5|≥|a2-a5|≥|a1-a5|这样的排列的个数N=1+2+22+2+1.
a1,a2,…,a7为1,2,…,7的排列,满足|a6-a7|≥|a5-a7|≥…≥|a2-a7|≥|a1-a7|这样的排列的个数N=1+2+22+23+22+2+1.
归纳猜想:a1,a2,…,a21为1,2,…,21的排列,满足|a20-a21|≥|a19-a21|≥|a18-a21|≥…≥|a1-a21|这样的排列的个数N=1+2+ 22+…+29+210+29+…+2+1=3 070.
思路2 利用数轴,一一罗列.
数轴上标号为i(i=1,2,3,…,20,21)的点记为Pi,共有21个点,a1,a2,…,a21分布在这21个点,|ai-a21|表示数轴上两点距离.
当a21在P1处,则ai(i=1,2,…,20)在Pi+1处,这样的排列数为N1=1.
红粘土作为特殊土中的一种土类,其特殊性质是由成分和结构控制的,而成分和结构取决于成因,所以对其特殊性的研究要从本质——成因入手。红粘土不同于一般土,不能简单的注重搬运与堆积方式,将其分为坡积物、洪积物、残积物等。其成因复杂,有着与其他土类不同的成土作用环节,不是简单的搬运与堆积所能反映的。对特殊土的研究,特别是红粘土,要从成土过程中各阶段的特征分析及成土的主要作用环节入手,两者相结合,这样才能正确认识和分析特殊土的性质,以便在工程实践中更好的应用。
当a21在P2处,则a1,a2在离P2距离为1的P1,P3两点,ai(i=3,4,…,20)在Pi+1处,这样的排列数为N2=2.
当a21在P3处,则a1,a2在离P3距离为1的P2,P4两点,a3,a4在离P3距离为2的P1,P5两点,ai(i=5,6,…,20)在Pi+1处,这样的排列数为N3=22.
……
当a21在P11处,则a1,a2在离P11距离为1的P10,P12两点,a3,a4在离P11距离为2的P9,P13两点,……,a19,a20在离P11距离为10的P1,P21两点,这样的排列数为N11=210.
当a21在P12处,则a1,a2在离P12距离为1的P11,P13两点,a3,a4在离P12距离为2的P10,P14两点,……,a17,a18在离P12距离为9的P3,P21两点,a19在P2,a20在P1,这样的排列数为N12=29.
……
当a21在P21处,则ai(i=1,2,3,…,20)依次分布在P21-i处,这样的排列数为N21=1.
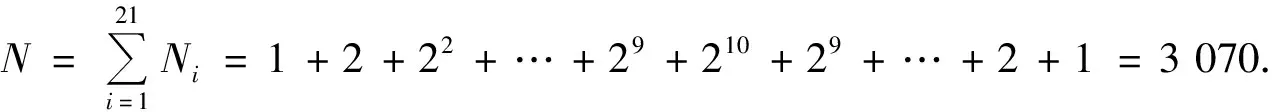
思路3 寻找规律,合理分类.

评析思路1通过特殊化思想的运用,先思考两次数字较少的情形,很容易得到相应的排列数,再通过归纳猜想,就很容易得到此题的正确答案.思路2很好地利用了数轴这个有力工具,在黑板上直观呈现,排好a21的位置后,让学生动手操作排ai的位置,随着a21的变化,学生很容易得出相应的排列数.思路3是在思路2的基础上发现了a21=i和a21=22-i,i∈{1,2,…,10}时,|ai-a21|的所有取值情况是一样的,因为存在对称性,所以设a21=k,只需考虑k∈{1,2,…,10,11}的情形.数轴上的操作已经让学生明白其基本原理,学生尝试总结,教师通过适当辅助,完成a2i-1,a2i为k-i,k+i的排列(若k=1,没有这样的i),且aj=j+1(2k-1≤j≤20)(若k=11,则没有这样的j)这样的规律总结.整个思维过程顺畅,简洁易懂,学生对解决此类问题所用的研究思路有了深刻感悟.
紧接着,笔者给出了以下题目让学生练习:已知数列ak=2k(k=1,2,3,…,n),则所有可能的乘积aiaj(1≤i≤j≤n)的和等于.
课堂上学生很快给出了如下两种思路:
思路1 列举找通项.
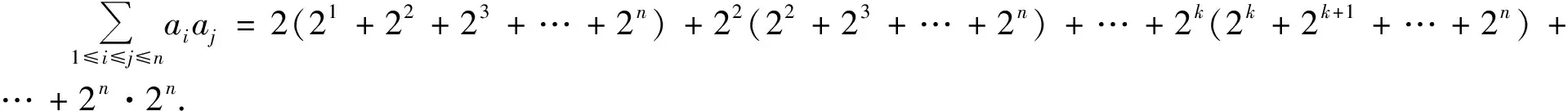
思路2 利用数表,直观呈现.

a1a1a1a2a1a3a1a4a1a5…a1ana2a1a2a2a2a3a2a4a2a5…a2ana3a1a3a2a3a3a3a4a3a5…a3ana4a1a4a2a4a3a4a4a4a5…a4ana5a1a5a2a5a3a5a4a5a5…a5an…………………ana1ana2ana3ana4ana5…anan

图1
评析练习与例题看似不相关的两个问题,实则所用的思想方法类似,都是通过特值开路、一一罗列后探求规律.而数轴、数表都是教材上常见的工具,通过这些直观工具的运用,在动手操作的过程中发现规律.练习思路1先是取i=1,罗列a1aj(1≤j≤n)所有项的和,再取i=2,罗列a2aj(2≤j≤n)所有项的和,接着找出通项为2k(2k+2k+1+…+2n),化简通项得2k+n+1-22k,最后为两个等比数列求和.竞赛题的思路2利用数轴,练习的思路2则利用数表直观呈现,学生通过观察可将数表分解为三个部分,由对称性知左右两部分各项和相等,中间和右边各项和即为所求.
如何提升优秀学生的数学思维,面对复杂问题,突破思维壁垒,是值得我们思考的问题.数学竞赛题复杂多变,怎样在错综复杂中寻找到最佳路线,需要的是巧做、化繁为简,利用常规思维方法来思考并解决复杂问题.学生通过动手操作,发现问题的本质规律,克服畏难情绪,增强学习信心,从而提高学习效率,形成优秀的思维品质和数学素养.
