基于核密度的电力线通信网络时延估计

毛珊珊，马胜国，魏本海，何先灯，冷安辉

（1.深圳市国电科技通信有限公司，广东 深圳 518109；2.西安电子科技大学，通信工程学院，陕西 西安 710071；3.深圳智芯微电子科技有限公司，广东深圳 518045）

电力线通信（Power Line Communication，PLC）网络是电力系统的重要支撑。为了更好地实施故障管理和网络优化，常常需要确定PLC 网络的拓扑结构[1]。一种做法是在智能电表上采集电量数据，构建Diff-Lasso 统计模型[2]，求解拓扑结构；另一种可行的方法是通过测量PLC网络节点间时延来构造拓扑。文献[3]设计了一种基于往返发送扩频调制信号进行时延测试的方法，时延测量精度达到10 ns，依据实测时延数据构造的拓扑正确率达到了90%。但在实际应用时，受电力网络中各种电器运行情况动态变化的影响[4]，测量得到的时延会产生较大涨落，这些因素包括电器类型、数量，以及电力线长度、节点数、节点位置等。目前未见降低家用电器对时延测量影响的文献报道。

核密度估计（Kernel Density Estimation，KDE）是一种不受分布约束的数学方法[5]，该方法可以从现有的样本数据中得出密度函数，已成功用在电力、目标检测、信息挖掘等多个领域[6-8]，也可用在互联网端到端带宽测试的结果估计中[9]。

为了获得节点间时延与电器动态化之间的关系，以准确估计时延值，文中建立了PLC 网络转移参数模型和PLC 设备间时延测试模型，通过核密度估计法对繁忙/空闲状态的时延进行估计。

1 电力线通信网中的时延分析

PLC 信道的传递函数可以表示为：

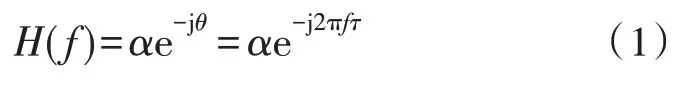
其中，α为路径衰减系数，θ为传递函数的相位，τ为路径时延。该时延主要为电磁波在电力线中的传播时延，也是文中要测量的目标。但是，低压台区的电力线上接入了大量的用电器，而这些用电器都有复阻抗，必然引起信道传递函数相位的变化，进而引起电力线传输时延的变化。

图1 所示为基于转移矩阵的传输模型，该模型给出了测量信号发射、传输及接收的等效电路，其中Es1为发射信号源，U1、U2分别为发端和收端电压，I1、I2分别为发端和收端电流。

图1 基于转移矩阵的传输模型

PLC 线路对应的转移矩阵为:

对于传输线，转移矩阵为:

其中，γ为传播常数，Z0为特性阻抗，l为传输线长度。

对于并联的用电器，转移矩阵为:

其中，Z1为并联用电器的阻抗。由图1 所示模型可得传递函数：

根据转移参数的级联特性，可将PLC 网络分解为若干级，分别由电器负载、传输线构成。PLC 线路的级联等效如图2 所示，其中TX1为发送节点，ZT1为信号源内阻，Zin1为网络阻抗，RX2为接收节点，ZR2为接收电路输入阻抗，Zout2为网络阻抗。图2 所示的拓扑包含三个并联电器负载，总的转移矩阵为:

图2 PLC线路的级联等效

在电力线拓扑、接入用电器情况改变时，总的转移矩阵A也不相同。为估计用电器对PLC 时延τ的影响，可改变拓扑和接入情况，计算出特定频率下转移矩阵A的相位，由式（1）计算得到传输时延τ。

2 用电器对时延的影响分析

2.1 仿真参数

选取常见截面积为2.5 mm2的平行电力线，其单位长度的电容C、电感L、电阻参数R0、电导参数G0及介质介电常数εr如表1 所示[10-11]。

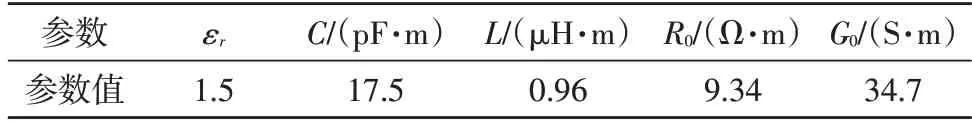
表1 2.5 mm2电力线参数

文中仿真使用的家用电器包括空调（Z=4.887+0.547j）、电灯（Z=1 609.11-84.69j）和加热器（Z=24.2）。

2.2 仿真结果与分析

选择图2 所示的拓扑，保持电缆主干长度不变（l1+l3+l5+l7=40 m），改变分支节点的位置（分别改变l1、l3、l5和l7的值），在不接入用电器或者分支1 接入空调、分支2 接入电灯、分支3 接入加热器的情况下，观察此时的信道传递函数的特性，仿真结果如图3 所示。

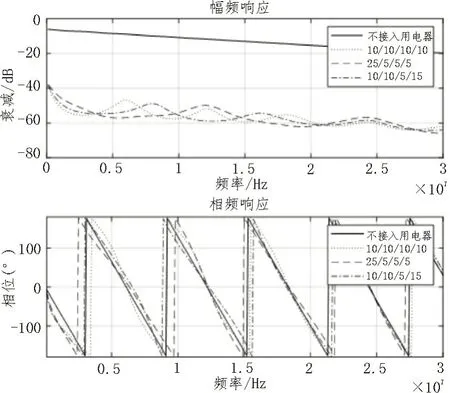
图3 不同用电器接入情况下的信道相应函数仿真结果

图3 中，所得的幅频和相频响应有较大差异，幅度随频率增大而减小，可见时延特性与是否接入用电器有关。接入用电器时，幅频和相频曲线有类似周期性的变化，各分支间的距离越接近时，幅频和相频特性变化的周期越小。可见，相频特性与PLC 网络拓扑密切相关，也即时延特性与电器接入位置密切相关（即使电缆长度相同）。

3 PLC时延测量和估计方法

3.1 PLC时延测量方法

电力线通信网络时延测试常常采用往返测试的方法。采用往返测试时延的原理如图4 所示。

图4 时延往返测试原理图

图4 中，TX1发送扩频信号给RX2，发送时刻为T1，接收时刻为T2，返回信号的发送时刻为T3，回到发送端的时刻为T4，以发送时钟为参考，接收时钟偏差为σ。

图4 中发射方TX1测量出的时延可表示为:

其中，Tp是从接收方收到测量脉冲至发出返回脉冲的处理时延。Tp可认为是常数，可以通过实验获得。这里假定是两个方向路径时延相同，收发双方电力线长度l为:

其中，c为真空中的光速，εr为电缆介电参数。

设测试信号的信息序列为a(t)，扩频码序列为c(t)，a(t)和c(t)均为双极性信号（即取值±1），载波角频率为ω0，则发射信号可写为：

由于多径信号较弱，这里只考虑直达路径。由式（1）可得，信道冲激响应为：

则接收机收到的信号为:

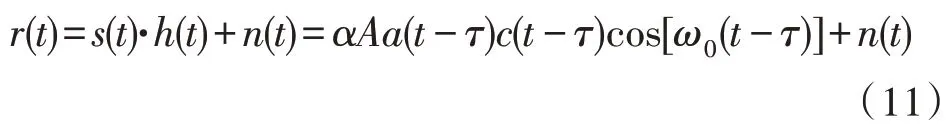
若采用相关解扩，则相关器的输出为：

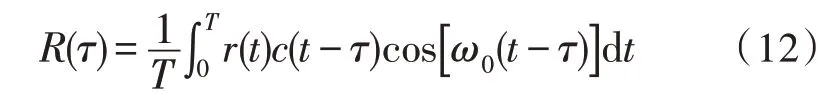
其中，T是信息比特（字符）周期，扩频码码片周期为Tc，T=NTc，N为扩频码码长。当R(τ)达到最大值时，τ为所测时延，可以通过搜索R(τ)最大值出现时刻即可得到时延的测量值。

3.2 常用PLC时延估计方法

3.1 节测量出来的时延包含了用电器干扰。为了消除电器噪声对时延测量的影响，进一步对测量的时延值进行估计处理。时延估计常采用密度估计方法。最常用的密度估计方法是统计直方图，其原理是将样本特征空间分成多个子空间。直方图密度估计虽然简单，但缺陷较多[13]：1）直方图划分区间时可能会导致信息丢失；2）直方图不是唯一的，难以对比；3）直方图往往不平滑；4）直方图不能很好地处理极值。

3.3 核密度估计方法

为克服直方图估计的缺点，文中采用核密度估计法来估计时延。核密度估计法属于非参数检验方法之一，是在概率论中用密度函数估计未知分布，由Rosenblatt 提出[5]。定义核函数K(t)满足：

在任意一点x的密度为:

其中，b为核宽度比，n是b×x内x的点数（h=b×x是核宽度），xi是测量得到第i个点的时延值[9]。选择不同的核宽度比会影响核密度估计的图形形状及光滑度[14]。

常见的核函数有均匀核函数、三角核函数、矩形核函数、高斯核函数等[15]。三角核函数可更方便地提取极值点处的信息，在电力负荷预测方面已有相关研究[16]，因此文中选用的三角核函数，如下:

其中，核宽度比b的选取对估计的性能有很大影响。

4 PLC时延测量与估计实

4.1 实验方法

文中采用Matlab Simulink 进行仿真，电力线部分采用RLCG(Resistance Inductance Capacitance Conductance，电阻电感电容电导)模型表示[17]，电器负载阻抗取测量值，测量频率为500 kHz，电力线特性和电器特性与第2 节相同，Simulink 仿真模型如图5所示。

图5 Simulink仿真模型

仿真模型中，收发模块相同，内部采用S-function编写，收发阻抗均为50 Ω。通过3.1 节给出的时延测量方法测量时延τ，进而采用直方图和核密度估计法对电器工作时的PLC 网络时延进行估计。

考虑实际生活场景中用电器数量的随机性，采用2.1 节相同特性的用电器，把空调和加热器接入数量均设置为0～3 个，灯的接入数量设置为0～5 个，上述用电器的接入种类和数量均为随机。

4.2 单个节点空闲/繁忙时的核密度估计结果

在主干长度为20 m 的电缆上，设置一个可接入用电器的节点，在该节点以一定概率随机接入用电器，进行多次仿真来模拟实际情形。此时，不接入用电器时的时延值为84.31 ns，通过改变接入用电器的概率来分别模拟空闲和繁忙时段的测试结果。设定空闲时段接入用电器的概率为30%，繁忙时段接入用电器的概率为70%，选取100 组依概率随机生成的数据，仿真结果如图6-7 所示。

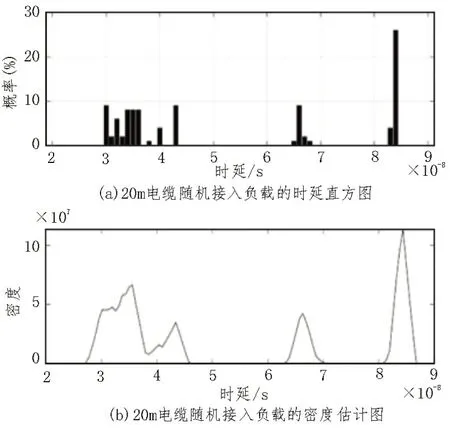
图7 繁忙时段的时延估计

空闲时段可选较大的b值(b=5×10-9)，此时估计图的包络更平滑。繁忙时段可选取更小的b值(b=1×10-9)，以消除用电器对时延测量的影响。对比直方图和密度估计图可知，两种估计方法均能估计出较准确的时延值，直方图估计所得的时延值为84 ns，核密度估计法估计所得的时延值为84.35 ns。

与不接入用电器时的时延值84.31 ns 相比，核密度估计法得到的时延误差为0.04 ns，而直方图法误差为0.31 ns，误差小了一个数量级。在实际测试中，往往采用逐级测试的方法来提高精确度，每一级误差的累积会使最终结果误差较大。

4.3 拓扑复杂时的核密度估计结果

考虑拓扑更复杂的情况，在两个节点随机接入用电器，用电器接入概率为30%，且两个节点的用电器接入情况相互独立时，时延估计结果如图8 所示。此时取b=5×10-9，核密度估计法所得的时延值为84.55 ns。

图8 复杂拓扑的时延估计

文中还仿真了不同环境下（包含不同节点数、不同接入概率和不同电缆长度）的时延估计，部分数据如表2 所示。

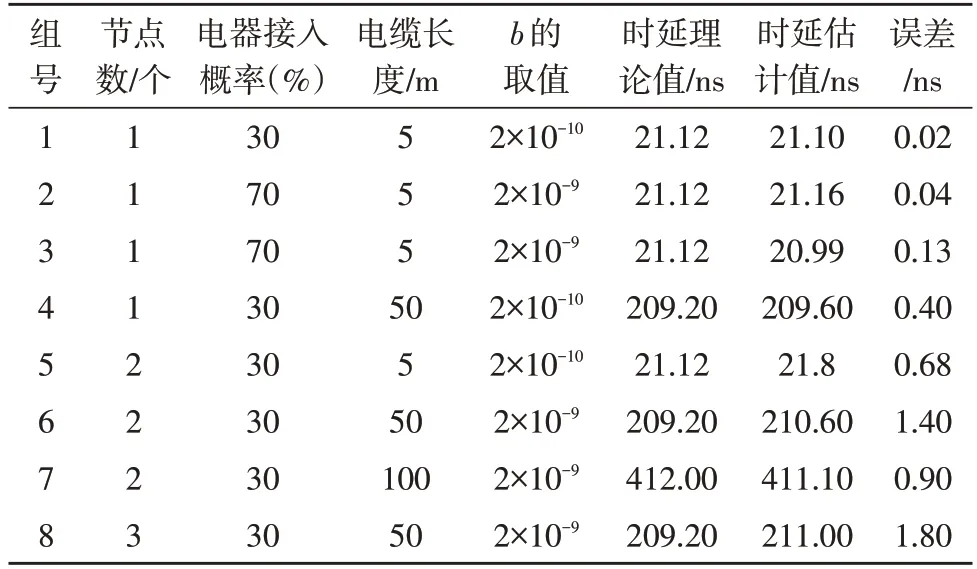
表2 不同环境的仿真结果

由表2 可以得出以下结论：

1）由1、2 组数据可得，电网运行状况（即用电器随机接入概率）对时延估计的影响较大，空闲状态估计的准确性更高；

2）由1、4、7 组数据可知，时延和电缆长度的关系近似线性；

3）由2、3 组数据可知，在电网繁忙时进行时延估计，需要选取更小的b值才有可能消除用电器运行带来的剧烈干扰；

4）由1、5 和6、7、8 组数据可知，用电器接入数量越多、电缆主干长度越短时，估计难度越大。

5 结论

文中建立了基于往返测试的PLC 通信网络时延估计模型，对影响时延测试结果的因素进行了分析。基于转移参数将PLC 网络分解为多个级联的子网络，并得出总的传递函数，由此得出不同拓扑的相位变化对时延的影响。用电器对时延的影响复杂，时延与用电器是否接入和接入位置均有关联。仿真结果表明，核密度估计法可有效降低电器对电力线时延测试的影响，文中研究对电力线通信网络性能优化、拓扑构造等具有重要的参考价值。