中小型压铸机企业装配车间AGV路径规划研究
2023-01-08罗冬梅鲁玉军张振涛
罗冬梅,鲁玉军,张振涛
(浙江理工大学机械工程学院,浙江杭州 310018)
0 引言
压铸机装配是中小型压铸机制造过程中的一个重要环节,装配流程主要分为机架部装、电气部装、柱架部装、油路部装、钣金部装和打料部装共6 步,根据物料配送计划由自动导引小车(Automated Guided Vehicle,AGV)从暂存区配送至装配工位。在整个配送环境中,密集区域与稀疏区域并存。其中,暂存区内部及工位之间的可行区域大,单个装配工位的零部件摆放密集。AGV 配送的零部件多数体积大、重量重,为防止零部件在配送过程中出现倾斜或损坏等情况,在密集区域及转弯处对AGV 行驶的平稳性要求非常高。
路径规划是实现AGV 自主导航的重要组成部分,合理的路径规划对于提高配送效率和安全性至关重要[1-2]。目前针对某一环境的路径规划算法通常分为两类:①基于已知环境模型的全局路径规划算法,包括A*算法、Dijstra 算法和遗传算法;②基于传感器信息的局部避障算法,包括DWA(Dynamic Window Approach)算法、TEB 算法和人工势场法[3-6]。鉴于A*算法利用启发式评价函数保证搜索方向与目标点一致,避免了对地图中所有点进行评价,相比于Dijstra 算法和遗传算法,具有快速实现最短路径规划的优势,因此本文以A*算法作为全局路径算法。考虑到整个配送环境中密集区域与稀疏区域并存,人工势场法在密集区域中路径不平滑,且易陷入局部最优解,TEB 算法在出现动态障碍物或速度控制量不平滑时,路径规划变化频率较高,令AGV 存在震荡和碰撞风险[7],而DWA 算法综合考虑了AGV 的运动模型与环境因素,更加符合真实AGV的运行需求,因此本文将DWA 算法作为局部路径算法[8]。
1 相关工作
目前针对A*算法的研究集中于对其规划的路径存在大量拐点、路径不平滑而展开[9-11]。其中,劳彩莲等[12]增加了对关键节点的提取,对前后点运动方向进行判断,将与前节点运动方向一致的节点视为冗余点;陈艺文等[13]将转折点作为局部目标点,利用混合A*进行二次规划;陈娇等[14]直接对节点之间的连线与障碍物的位置关系进行判断,识别冗余节点,去除冗余路径。针对DWA 算法的研究主要集中于AGV 小车在障碍物密集环境中成功率不高或容易出现绕行而展开。王永雄等[15]和吴宇等[16]利用移动机器人自带的传感器获取的环境信息结合自适应思想,实现DWA 评价函数的权重自适应调节;陈志明[17]通过设置机器人与目的地的距离增量为DWA 算法评价函数,加快了机器人朝目标点前进。
以上文献针对A*算法的改进集中于对已有路径节点的筛选,而缺少对转角较大处节点的优化,因此本文设计双层优化A*算法,在去除冗余节点的基础上,调整转角大小,以提高路径平滑度。改进后的A*算法更加符合AGV小车的运动模型,并提出转向成本函数来调整DWA 算法的评价函数,以确保小车的运动更加贴合A*算法规划的路径,避免不必要的转弯,最终为AGV 在压铸机装配车间提供高质量的可通行路径。
2 AGV路径规划全局算法
2.1 A*算法基本原理
A*算法结合给定的起点和终点信息,通过对可行节点的搜索与评价,求解最短路径。在进行节点搜索的过程中,将确定为路径的节点称为父节点存储于Closed 集合,将与父节点相邻且可到达的节点(子节点)存储于Open 集合,通过函数(fn)对子节点的成本值进行估计,将成本值最小的子节点看作新的父节点[18],步骤如下:

其中,g(n)为起点到当前子节点的实际成本值,h(n)为当前子节点到终点的成本估计值。
Step 1:初始化Open 集合、Closed 集合,将起点P1添加至Open集合中。
Step 2:获取与起点P1邻近且可到达的节点作为子节点添加至Open 集合中,将起点作为父节点从Open 集合转移至Closed 集合中。
Step 3:计算各个子节点的(fn)值,并将(fn)值最小的点作为新的父节点Pi,从Open集合转移至Closed 集合中。
Step 4:检查与新的父节点邻近且可到达的节点,如果某相邻点不在Open 集合中,则添加;如果已在Open 集合中,则计算该点对应的g(n)。如果新的g(n)值更低,则更新父节点为当前点并重新计算(fn),否则保持不变。
Step 5:重复Step 3、Step 4,直至Open 集合中出现目标点Pn,或Open集合为空。
2.2 改进A*算法
针对A*算法规划得到的路径存在大量拐点、路径平滑度低,从而影响AGV 平稳运行的问题,本文提出一种改进的A*算法,如图1所示。
对A*算法规划出的路径节点集合{P1,…,Pn},当n>2时,进行两阶段优化处理:第一阶段提取路径节点并消除冗余节点,实现部分转弯路径变直;第二阶段增加节点密度,调整转角大的节点坐标,减小转弯幅度。具体步骤如下:
第一阶段:提取节点,去除冗余路径。
Step 1:连接各节点。将节点Pi依次与集合{Pi+1,…,Pm,…,Pn}中的节点连接。
Step 2:判断并消除冗余节点。当节点Pi与节点Pm-1的连线之间不存在障碍物且与节点Pm的连线之间存在障碍物时,定义节点Pi与节点Pm-1之间的节点为冗余点,即集合{Pi+1,…,Pm-2}为冗余点,并将其删除。
Step 3:以节点Pm-1为起点与集合{Pm,…,Pn}中的点依次作连接,判断冗余节点,以此类推,当i=n-1时停止。
Step 4:连接剩余节点,获得新路径。
第二阶段:增加节点密度,调整转角大的节点坐标,减小转弯幅度。
首先,对新路径的节点进行遍历,当两节点之间的距离大于或等于设定值时(见式(2)),通过插入中点增加节点密度(见式(3))。
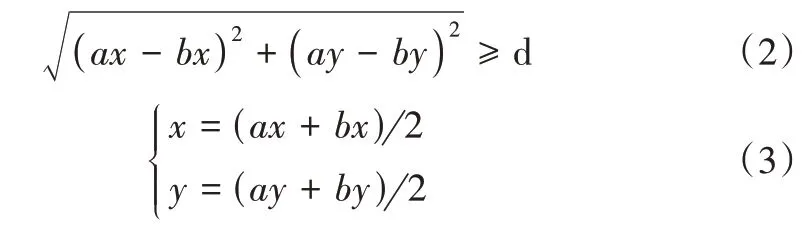
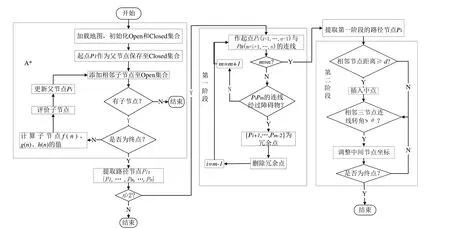
Fig.1 Flow of improved A*algorithm图1 改进A*算法流程
然后,再次遍历节点,利用式(4)计算连续3 点(C(cx,cy)、D(dx,dy)、E(ex,ey))之间的转角,之后通过式(5)依次比较转角与设定角θ的大小。对于转角大的情况,利用式(6)调整中间节点的坐标,以获得新路径、减小转弯幅度。
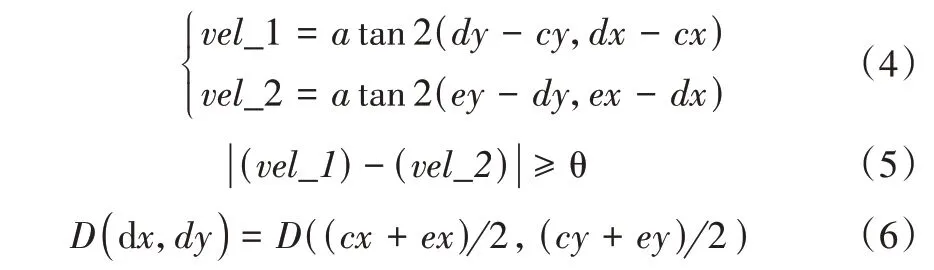
本文通过MATLAB 仿真对改进前后A*算法获得的规划路径进行对比,结果如图2 所示。其中,采用A*算法规划的路径如图2(a)所示,明显存在较多折点;利用改进A*算法规划的路径如图2(b)、2(c)所示,图2(b)经过第一阶段的拉直处理,删除了部分节点,路径较图2(a)更加平滑,图2(c)为经过第二阶段处理后的最终路径,进一步提高了路径的平滑性,并缩短了路径长度,即最大转角从45°减小到30°,路径长度由最初的8.66缩短到8.3。
3 AGV局部路径规划算法
3.1 动态窗口算法基本原理
DWA 算法将满足约束的速度采样空间定义为动态窗口,通过遍历窗口中的线速度和角速度,结合运动模型推算出多条路径,再利用评价函数对路径进行评分,将得分最高的路径作为最优路径[19-20]。
3.1.1 机器人运动模型
由于AGV 在单个采样周期ρt 内的运动距离短,运动轨迹被视为直线,通过式(7)计算AGV 在ρt 时段内x、y方向的速度变化量,即可得到ρt 时刻之后的位置信息(xt+1,yt+1,θt+1)(见式(8))。

3.1.2 采样空间
AGV 机器人在单个采样周期内的采样空间应同时满足3 个窗口:根据AGV 速度和角速度限制,形成窗口Vs;根据障碍物的距离,形成满足避障要求的窗口Va;根据电机力矩限制得到机器人在采样期间实际能够达到的速度,形成窗口Vd。
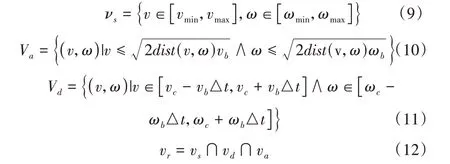
其中,vc、wc分别是AGV 当前的线速度、角速度;va、wa分别是AGV 的正向最大线加速度、角加速度;vb、wb分别是反向最大线加速度、角加速度;dis(tv,w)是速度为(v,w)的轨迹离障碍物最近的距离。
3.1.3 评价函数
在得到AGV 小车的运行轨迹后,结合环境设置评价函数G(v,w),用于挑选出最优轨迹,如式(13)所示:

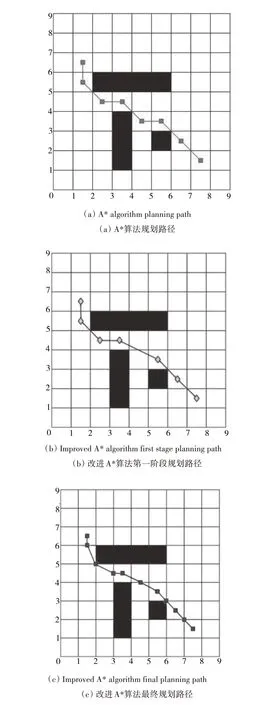
Fig.2 Results of global path planning图2 全局路径规划结果
其中,Pdist 为到最邻近全局路径点的距离;Gdist为到局部目标点的距离;Obs用于判断轨迹与环境障碍物是否有重合,当轨迹与障碍物重合时,返回负成本值,即轨迹无效,否则返回零成本值。
3.2 改进动态窗口评价函数
DWA 算法路径规划的成果主要取决于对评价函数的设定,在压铸机装配车间中,对AGV 行驶的平稳性要求很高。对此,本文引入全局方向Dir成本函数来衡量AGV 局部路径与全局路径在前进方向上存在的差异,确保局部路径与全局路径的前进方向尽可能一致,以防止运行过程中不必要的转向。具体原理如图3所示。
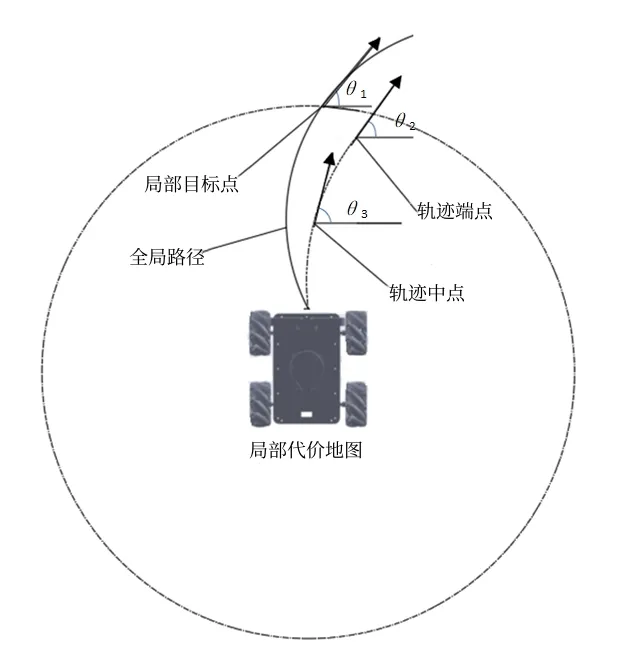
Fig.3 Global cost principle diagram图3 全局方向成本原理图
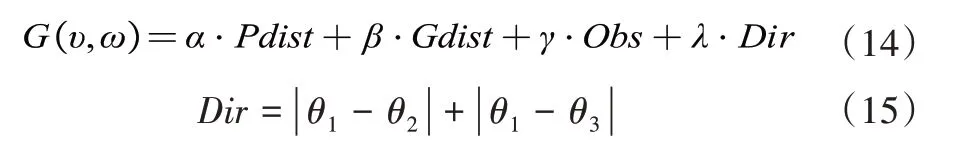
其中,θ1为全局路径中提取的局部目标点切线方向与x方向的夹角,θ2为局部路径规划的轨迹端点切线方向与x方向的夹角,θ3为局部路径规划的轨迹中点切线方向与x方向的夹角。
4 实例概述
本文以K 公司压铸机装配车间作为AGV 应用环境,如图4所示。
每个装配工位有多辆物料车装载零部件,由AGV 小车从暂存区1、2 配送至装配区。考虑到AGV 在执行任务过程中需要转弯,避障时的路径平滑度是本文对路径规划算法评价的重要指标,栅格化的地图更加符合需求,因此本文采用SLAM 创建栅格地图,如图5 所示。其中白色部分为可通行区域,黑色部分为不可通行区域,灰色部分为雷达无法探寻的未知部分[21]。
将改进的全局路径规划A*算法和改进的局部路径规划DWA 算法导入ROS 智能小车中,关键参数设置如下:l=0.05 m,θ=45,最大角速度为5 rad/s,最小角速度为0 rad/s,最大线速度为0.5 m/s,最小线速度为0 m/s,采样周期为1.0 s,α=64,β=24,γ=0.5,λ=25。
全局路径规划结果如图6 所示。其中,图6(a)、图6(b)为A*算法规划的结果,图6(c)、图6(d)为改进A*算法规划的结果,优化后的全局路径明显比优化前平滑。
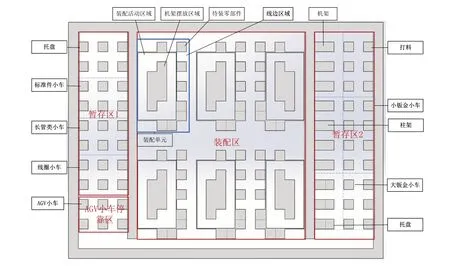
Fig.4 Workshop environment图4 车间环境
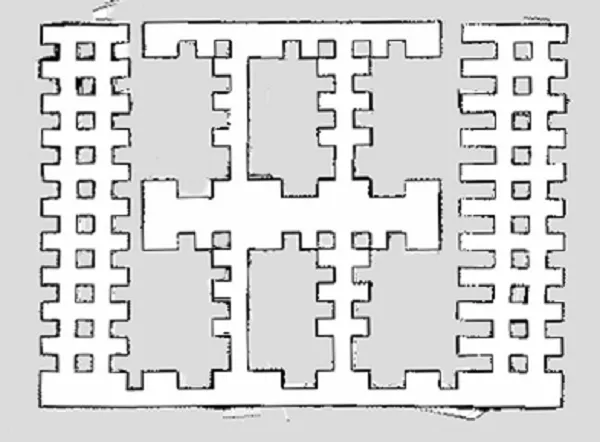
Fig.5 Grid map图5 栅格地图
局部路径规划结果如图7所示,改进前的局部路径与全局路径方向并不一致,小车行驶过程中会出现绕行的情况。改进后的局部路径与全局路径更加贴合,通过小车的实际路径图可知,改进后的转角幅度更小,如图8所示。对应的角速度变化曲线如图9所示,纵坐标为AGV小车的角速度,横坐标为小车启动后的时间,改进后的角速度集中在0.00~0.25区间,存在较少突变情况。综上所述,本文优化后的路径规划算法使小车在运输物料过程中能更平稳地行驶。
将AGV 小车置于密集环境中,对改进前后的算法分别执行50 次,通过的成功率如表1 所示,从表中可看出改进后算法的成功率远高于改进前。
AGV 小车利用改进前的算法规划路径时,由于算法自身存在的不足,规划的路径存在较大折点,无法使AGV 小车正常通行,导致小车会出现原地打转无法前进的情况,如图10(a)所示。改进后的算法路径规划如图10(b)所示,小车的转角变化较小,在一定程度上避免了AGV 不必要转向的同时,提高了路径的平滑度,使小车更适用于障碍物密集环境。
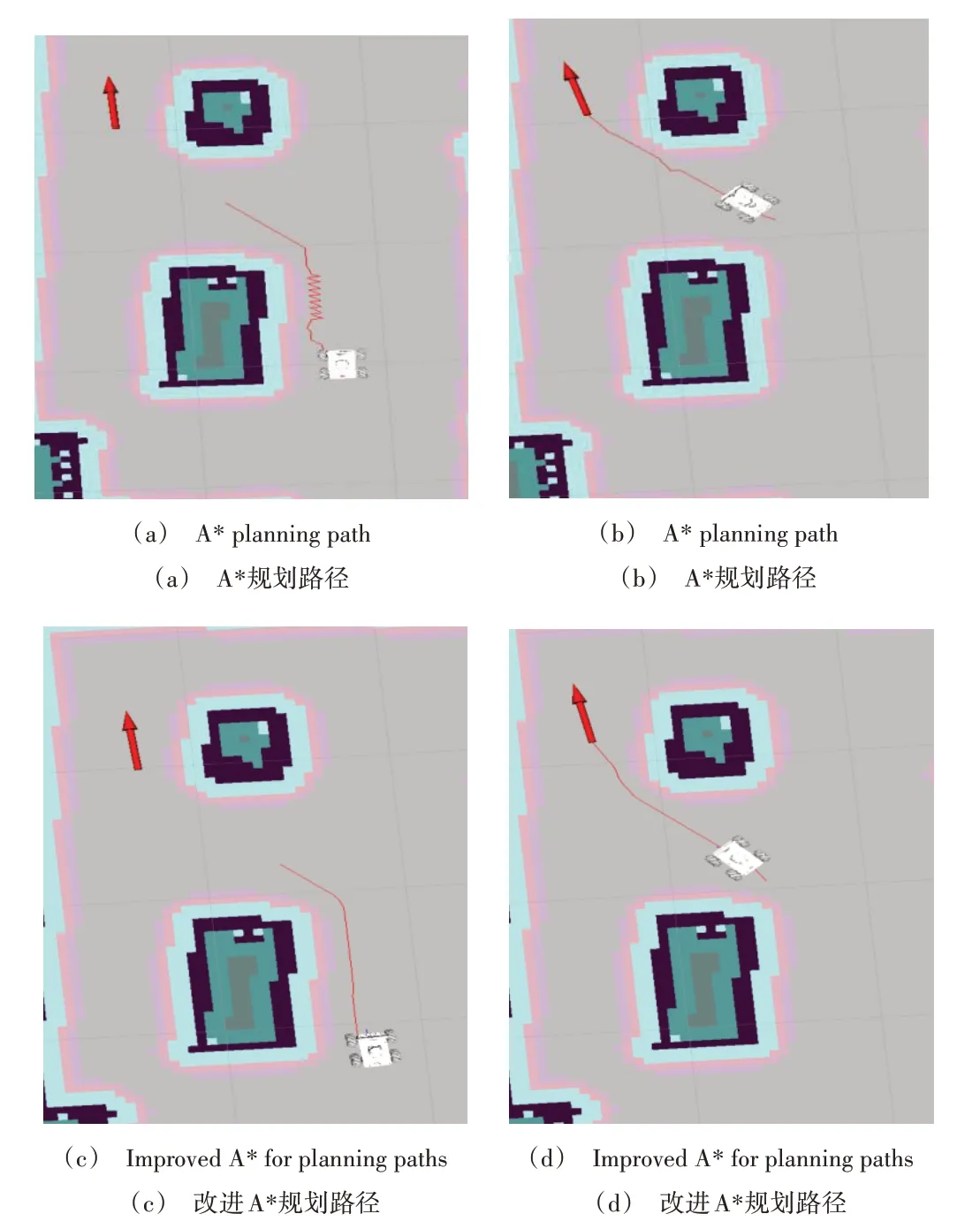
Fig.6 Comparison of global path planning图6 全局路径规划对比

Table 1 AGV success rate表1 AGV小车成功率
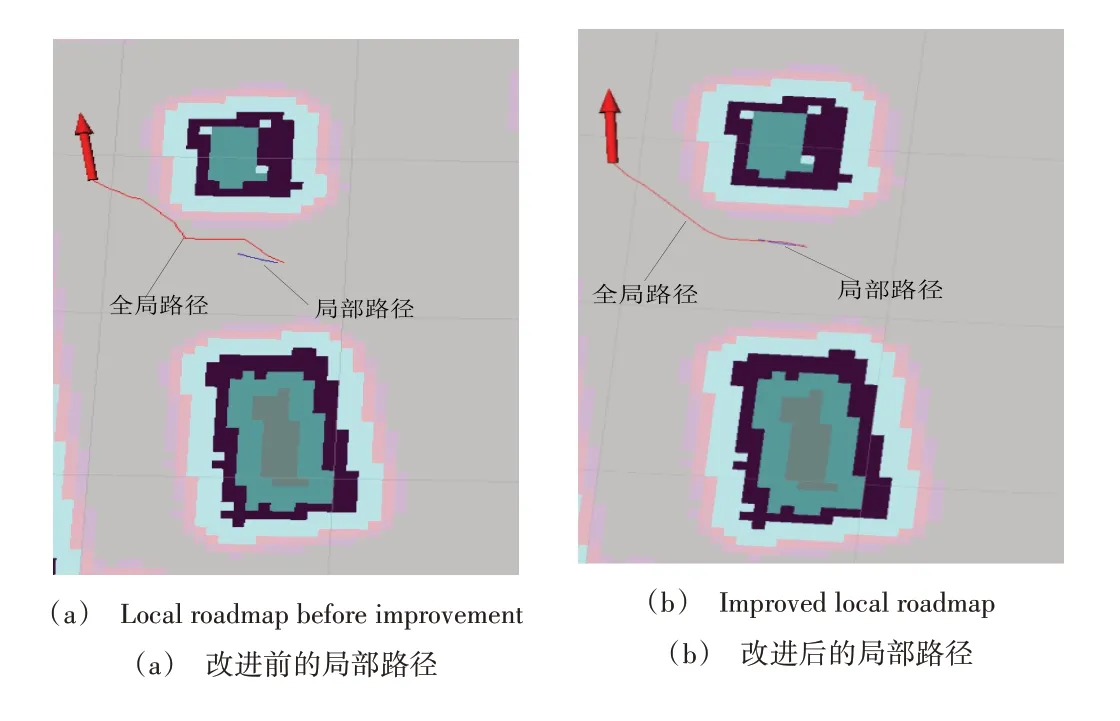
Fig.7 Comparison of local path planning图7 局部路径规划对比
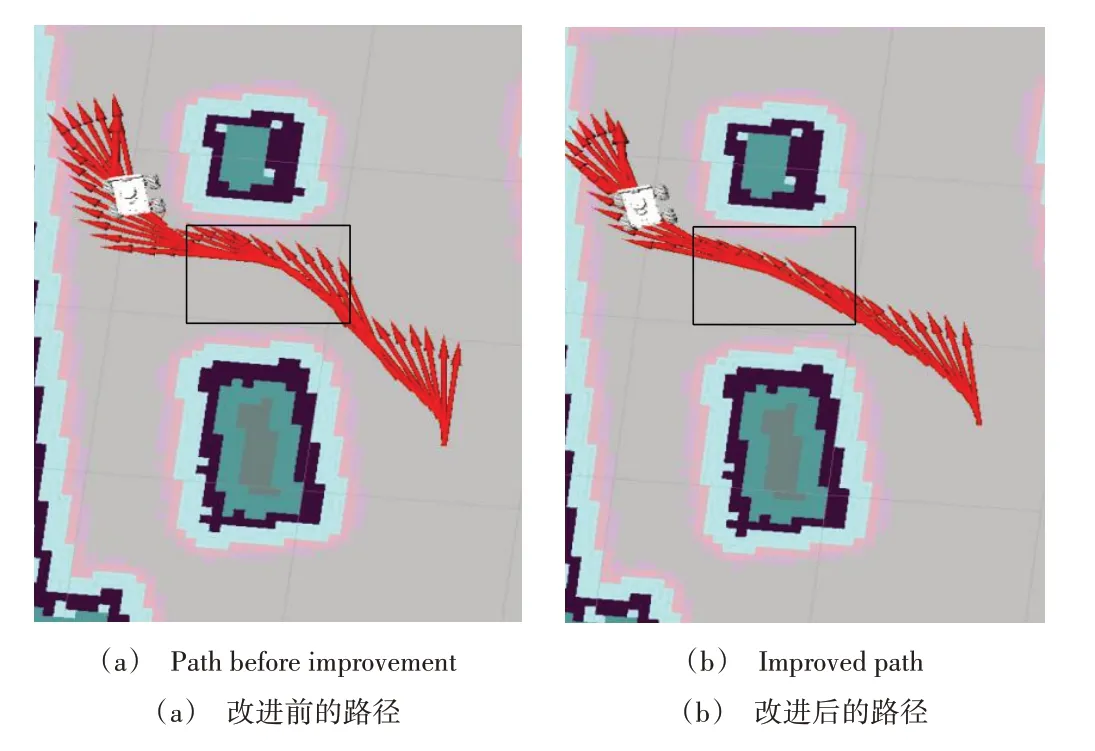
Fig.8 Comparison of actual path图8 实际路径对比
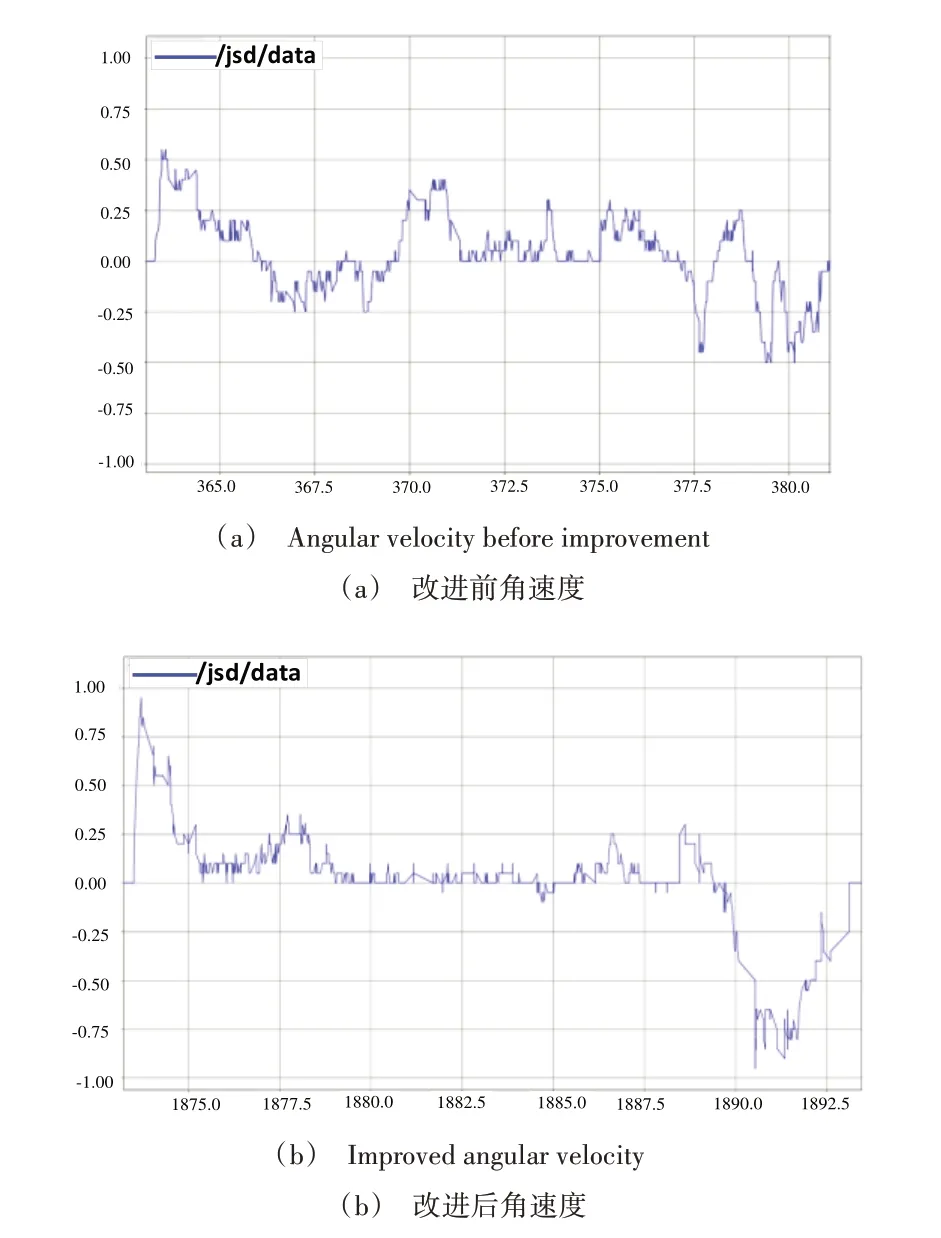
Fig.9 Angular velocity comparison图9 角速度对比
5 结语
本文针对压铸机装配车间,提出基于A*算法和DWA算法的AGV 小车路径优化算法,主要创新点如下:
(1)针对A*算法规划的路径存在大量拐点、不平滑等问题,通过识别冗余节点,去除冗余路径,增加节点密度,调整转弯大的节点坐标,提高了路径平滑度。
(2)考虑AGV 运动约束,采用DWA 算法。通过对其评价函数进行设定,弥补了AGV 小车容易出现绕行的缺陷。
(3)在压铸机装配车间环境中利用AGV 小车进行仿真实验,结果表明,AGV 能够平稳、快捷地到达目的地。
同时,本文方法也存在一些不足,需要深入研究相关技术,以提高AGV 小车的平稳性。今后将更全面地考虑影响AGV 小车路径规划的因素,提高AGV 小车在车间环境中的适用性。
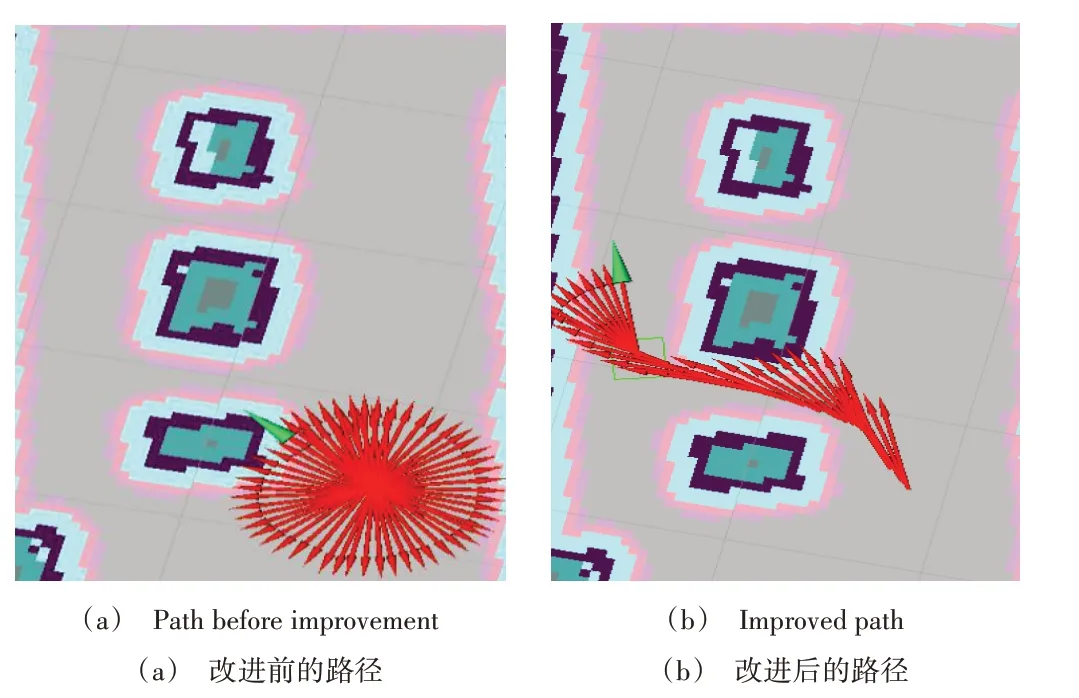
Fig.10 Comparison of dense environment path planning图10 密集环境路径规划对比
