基于改进灰狼进化算法的六轴机器人时间最优轨迹规划

段昊宇翔，张 宇，陈昊然，张倩玉

（昆明理工大学机电工程学院，云南昆明 650500）

0 引言

随着机器人学科的不断发展，业界内外对机器人运动能力、使用寿命等一系列性能指标提出了更高的要求。机器人轨迹规划对生产效率和使用寿命会产生直接影响［1］，如何规划机器人运动轨迹方式具有重要研究意义。

工业机器人的轨迹规划是指在满足工作要求和机械臂硬件限制的情况下，对预期运动轨迹进行规划［2-3］。从数学分析的角度讲，就是给机器人的路径赋予上时间的信息，即在某时刻规定机器人特定的位置、速度、加速度。机器人时间最优规划是轨迹规划中一个非线性且非常复杂的研究课题。近年来，国内外学者针对工业机器人时间最优轨迹规划取得了许多研究成果。代瑞恒等［4］提出一种改进量子遗传算法的机器人关节轨迹优化，但未考虑机器人动力学约束；浦玉学等［5］提出一种以改进引力搜索算法为基础的最优控制轨迹规划，但加权因子的使用主观性太强，缺乏科学依据；张慧敏［6］使用改进模拟退火算法处理三轴机器人时间最优问题，其并未对位置维度进行规划，且三轴机器人的适用性不强。此外，由于使用的是三次多项式进行插补，加大机器人运动过程中的振动与冲击。因此，本文在5 次多项式插值的基础上，考虑运动学［7］和动力学约束条件，提出使用改进灰狼进化算法在时间维度上对轨迹进行优化的方法，通过点到点（P2P）的方式达到预期轨迹，并使用MATLAB 软件进行仿真分析，验证此方法的可行性与有效性。

1 机器人建模

本文以自主研发的HW700 型机器人为研究对象，其三维模型如图1 所示。使用传统的DH 参数描述方法［8］建立机器人运动学模型，模型参数如表1所示。

Fig.1 3D model drawing of the research object图1 研究对象的三维模型

Table 1 DH parameters表1 DH参数

其中，θi表示关节的角度变量，αi表示关节的扭转，ai表示关节偏距，di表示杆长。

机器人动力学是研究机器人的运动条件和力矩之间关系的学科。其中，正向动力学是已知机器人的力矩条件和上一时刻的运动状态可以得出下一时刻的运动状态；逆向动力学是指在已知机器人运动状态和速度的情况下能得到机器人各关节的力矩，本文提到的动力学是逆向动力学。一般而言，机器人动力学建模分析一般有两种方法［9］：牛顿—欧拉法和拉格朗日—欧拉法。牛顿—欧拉法分析动力学的优点是可以知道所有连杆生成运动的方向以及大小，但缺点是分析太过复杂，这将导致出错的概率就会极大提高；而拉格朗日—欧拉法分析动力学是以能量的角度看待系统。虽然两种方法在分析时选用的角度不一样，但两者分析结果相同。本文结合虚功定理使用拉格朗日—欧拉法得到关节i运动时的广义力矩表达式由式（1）—式（5）所示［10］。

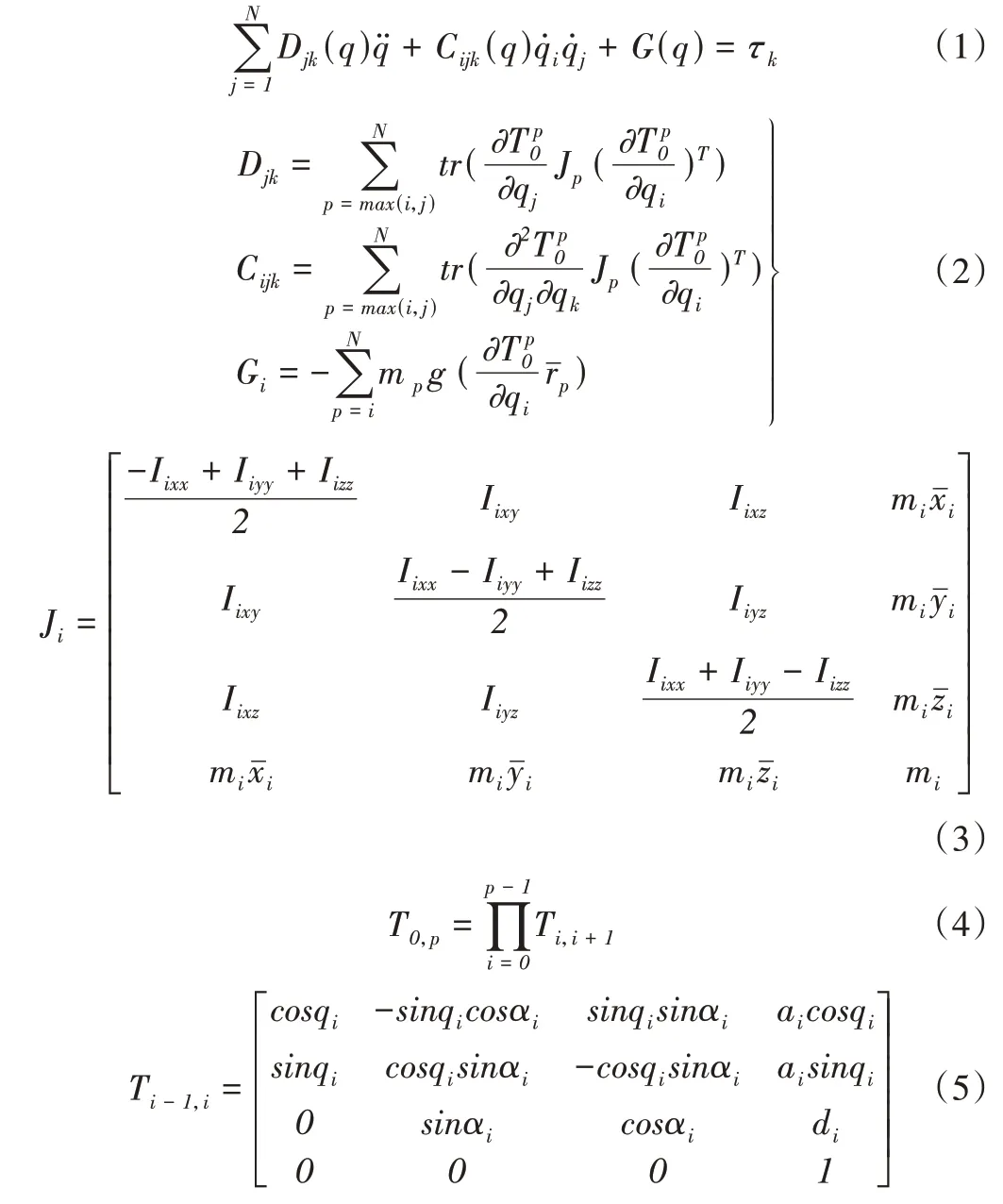
式中：τi表示关节i的广义力矩；qi表示关节的转角角度表示转角角速度表示转角角加速度；g表示重力矢量表示p 杆的重心的位置向量；Ti-1，i表示相邻杆件之间的坐标变化矩阵；Ji表示i杆的惯性矩阵；mi表示杆件质量；xi、yi、zi表示i杆的质心坐标；Iixx、Iiyy、Iizz表示i杆的惯性矩［11］；Iixy、Iiyz、Iixz表示i杆的惯性积。

2 轨迹规划问题描述

根据工作需求，设定目标路线，机器人末端需经过按顺序N个目标点，qi，n表示第i个关节在通过目标点Pn（n=1，2，…）时所对应的关节角度。为了使机器人末端的运动轨迹平滑，即机器人各关节可以平稳运动，需保证关节插补函数平滑且连续，一般情况下使用多项式插补的方式，本文选用式（6）所示的五次多项式进行轨迹插补［12］。

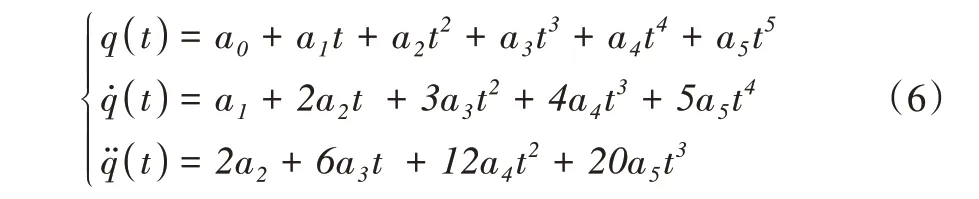
从目标点i到目标点i+1，两个端点处的位置约束条件由式（7）所示。

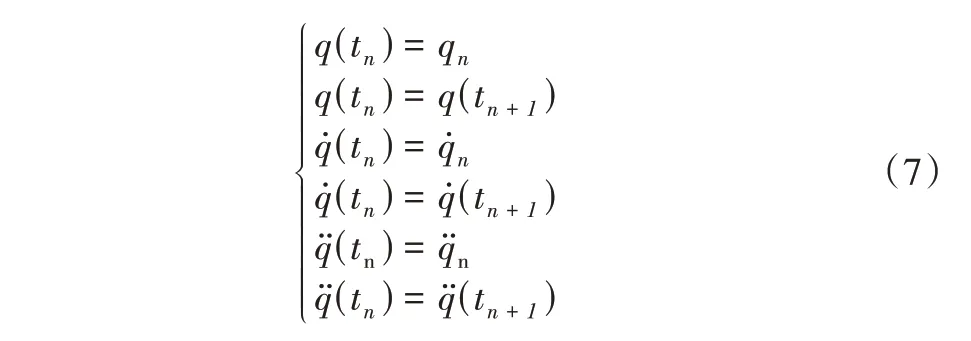
联立式（6）和式（7），得到每个关节的多项式系数由式（8）所示。

在机器人运动过程中，机器人在满足经过给定路径点条件下，同时满足机械臂的运动学和动力学约束并以最短时间顺利完成给定任务，提高运动效率。本文数学模型构建如式（9）—式（10）所示，机器人运动学约束和动力学约束具体数值如表2所示。

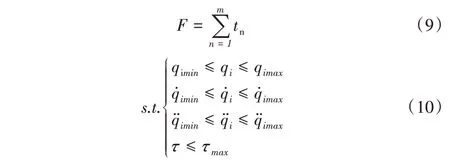
式中：qmin、qmax表示第j个关节的极限旋转角度；表示第j个关节的最大角速度、最大减速度；表示第j个关节的最大角加速度、最大角减速度；τmax表示各关节能承受的最大广义力。

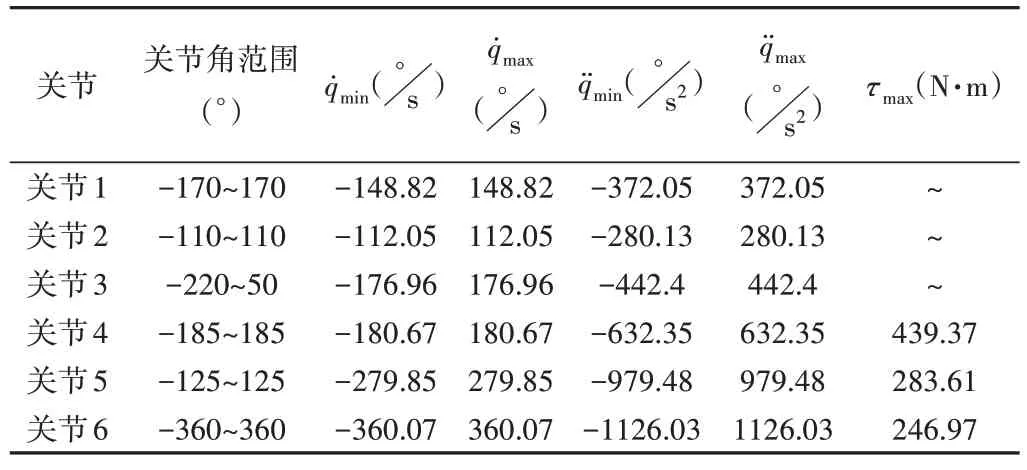
Table 2 Binding conditions表2 约束条件

3 改进灰狼进化算法

一般而言，用多项式进行规划轨迹时需要预先人为设定每一段轨迹中间的时间、位置、速度等一系列先决条件，但是如果已经提前规划了时间等一系列条件就无法对时间再作优化处理［13-14］。因此，本文选用自适应智能算法寻找最优时间轨迹，即在一个取值范围内，计算机通过设计的智能算法在约束条件下自动寻找函数最优值。在智能算法选择上，灰狼优化算法（Gray Wolf Algorithm，GWO）收敛速度快、稳定性好，不会因为意外输入而引起算法错误，具有很强的局部搜索能力。然而，灰狼优化算法存在易陷入局部最优、早熟的缺陷，导致其在处理复杂的工程优化问题时收敛精度不高。王俊等［15］将改进灰狼算法应用于医学问题之中，解决了其领域中“维数灾难”的问题。鉴于此，本文提出改进灰狼进化算法（M-DEGWO），即在灰狼优化算法的基础上引入差分进化算法（Differential Evolutionary Algorithm，DE）以改善灰狼优化算法易早熟、停滞等不足，从而更好地去寻找机器人在时间维度上的最优轨迹［16］。

3.1 灰狼算法

灰狼优化算法受狼群野外生存的社会等级制度启发［17-18］，搜索部分的等级制度分为头狼（Alpha 狼）、二号狼（Beta 狼）、三号狼（Delta 狼）、四号狼（Omega 狼）。算法逻辑部分也遵循着狼群攻击猎物的过程，首先寻找猎物阶段，其次是围捕猎物阶段，最终是进攻猎物阶段。Alpha 狼群中的个体，在整个种群当中属于决策阶级，主要任务是带领种群在狩猎过程中去决定探索方向和管理狼群分布等。Alpha 狼、Beta 狼、Delta 狼、Omega 狼依次为适应度最好的4 个个体，其中Omega 狼为候选解。在空间中，通过Alpha 狼、Beta 狼、Delta 狼去引导狼群不断向猎物位置靠近，从而找到猎物并进行攻击。建立这一行为的数学模型如式（11）—式（12）所示。

式中：D表示猎物与个体的距离；t表示当前迭代次数；表示协同系数向量表示猎物的位置向量；表示实时狼的位置向量。

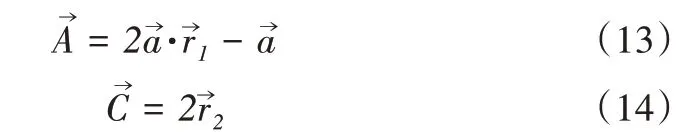
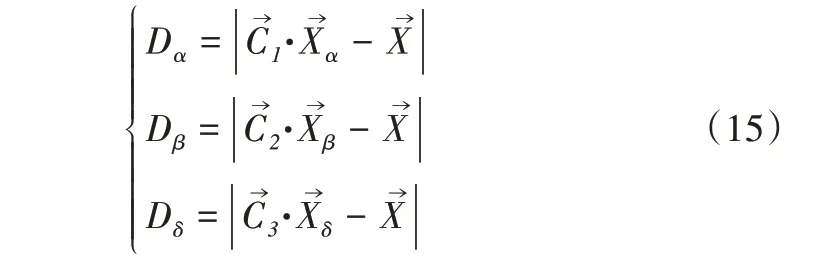
3.2 非线性控制参数策略

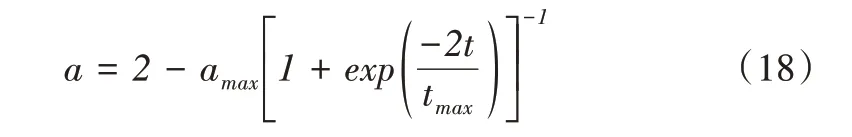
式中，tmax表示迭代次数。

3.3 狼群进化

Alpha 狼、Beta 狼、Delta 狼作为进化的父代，通过求出适应度次优的两头狼差值并与变化的搜索因子结合［20］，再与头狼相联系产生变异代，其变异代生成式如式（19）所示。

其中，W 为动态变化的搜索因子，其变化规则如式（20）所示。

变化的搜索因子可改善传统灰狼算法在收敛精度和搜索频次方面的缺陷，搜索因子W和当前迭代的次数t相关，前期当t小时，搜索因子W大，提高了算法的全局寻优能力和个体变异范围；后期随着迭代的进行，t逐渐变大，搜索因子W变小使算法有了更强的局部寻优能力。

新生成的子代个体由父代个体和突变代个体择优提供，在满足物竞天择的法则之下优胜劣汰，如果产生适应度更优的个体，则会淘汰原本父代中的不良个体，逐步让狼群向着正确的方向搜索。

3.4 改进灰狼进化算法

改进灰狼进化算法流程如图2所示。

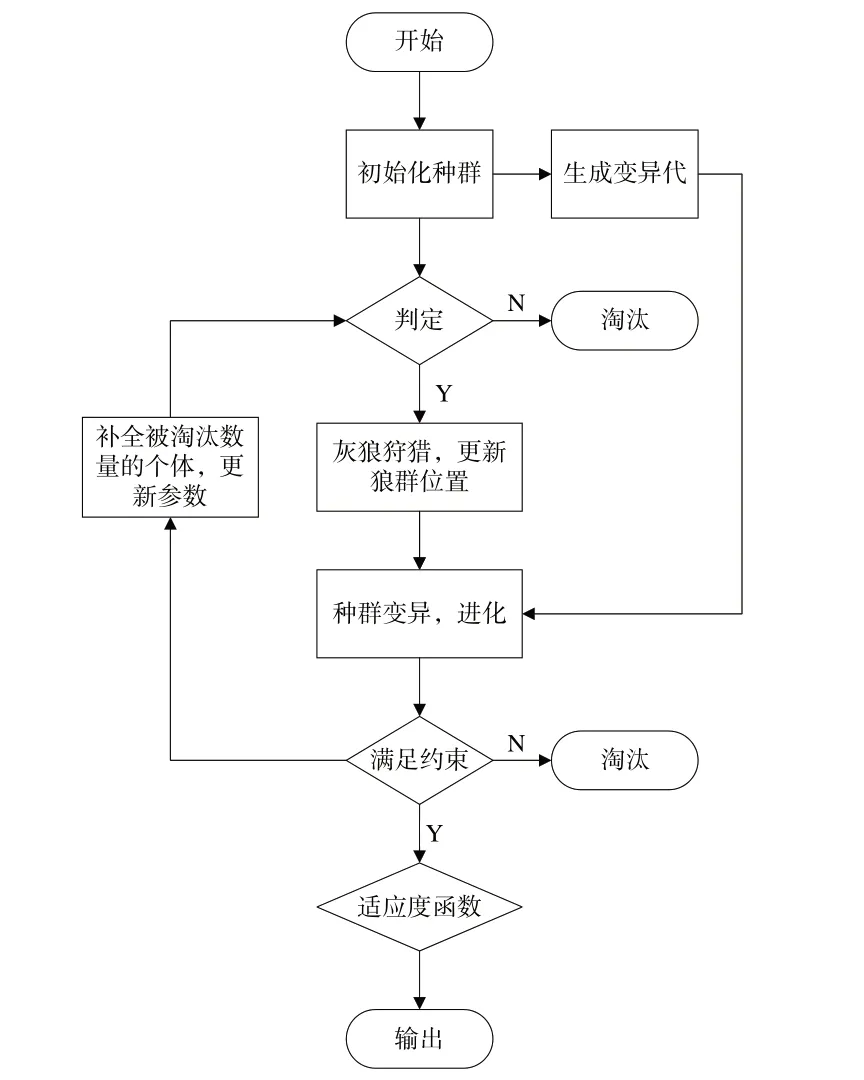
Fig.2 Flow of modified grey wolf evolutionary algorithm图2 改进灰狼进化算法流程

算法步骤如下：

Step1：输入种群规模大小N、最大迭代次数MaxIt、交叉概率PCR、变异概率pumt。

Step2：初始化父代种群{Xi，i=1，2，…，N}，初始化子代种群（child）、突变种群（mutant）。

Step3：将父代种群的个体代入约束条件一（机器人运动学约束）和约束条件二（机器人动力学约束）中，满足约束条件的个体生成父代种群，不满足条件的个体被淘汰。

Step4：计算父代灰狼个体适应度并记录精英狼Xα(t)、Xβ(t)、Xδ(t)的位置、数值大小。

Step5：根据收敛因子a计算出A1、A2、A3的数值，更新的数值并记录的位置。

Step7：将子代种群的个体代入约束条件一（机器人运动学约束）和约束条件二（机器人动力学约束）中，满足约束条件的个体进入新的父代种群，不满足条件的个体将被记录数量并淘汰。

Step8：记录当代适应度最优个体（最小值）并与前代适应度最优个体进行比较，同时在新的父代种群中重新生成与不满足条件个体相同数量的个体，更新收敛因子a等参数。

Step9：输出历史最优个体。

4 仿真结果及分析

为了验证本文改进策略对轨迹优化的效果，规划了一条由起点P1 和中间点P2 到终点P3 组成的典型搬运工作路径，并使用智能算法对该路径进行轨迹优化仿真试验。路径具体参数如表3所示。

Table 3 Track location表3 轨迹位置

改进灰狼进化算法参数设置为：种群规模大小N设为100、最大迭代次数MaxIt设为500、交叉概率PCR设为0.7、变异概率pumt设为0.9。差分进化算法的参数设置为：种群规模大小N设为100、最大迭代次数MaxIt设为500，缩放因子W设为0.6，交叉概率PCR设为0.7。灰狼算法的参数设置为：种群规模大小N设为100、最大迭代次数MaxIt设为500。3种算法初代个体的产生范围都为[0，10]。

表3 中，P1、P2、P3 为关节空间中机器人3 个不同时刻的位姿，由于M-DEGWO 算法为自适应算法，为了减少随机性，运行5 次收敛值后取平均值的结果与灰狼算法、差分进化算法在相同约束条件和目标函数下对于寻优时间寻优精度进行比较，结果如图3所示。

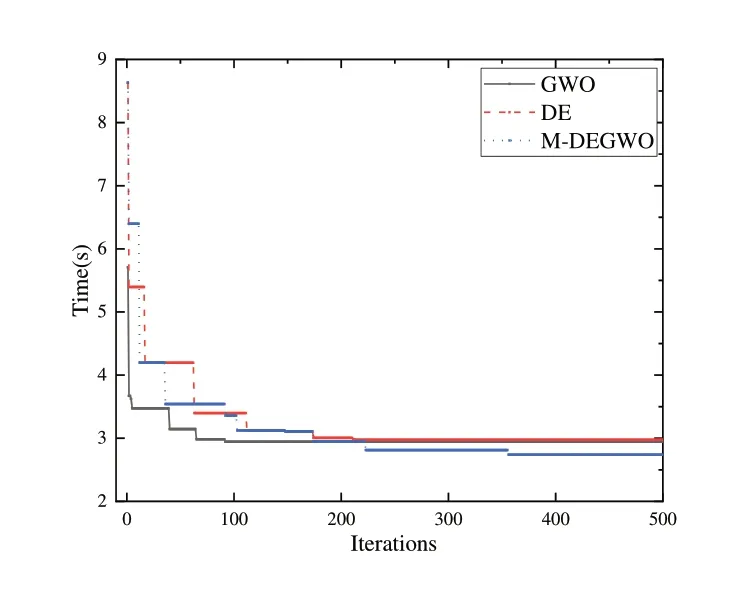
Fig.3 Algorithm optimization chart图3 算法寻优图

结果显示，改进灰狼进化算法相比于差分进化算法收敛速度更快、精度更高，且对父代个体做了预处理；相对于灰狼算法收敛精度更高，通过引入非线性收敛因子和动态的缩放因子，改善了灰狼算法易陷入局部最优、早熟的问题。结合上文所述的机器人动力学建模及轨迹规划问题描述，经过改进灰狼进化算法对5 次多项式插值进行时间优化后，利用MATLAB 软件对其进行编程分析得到其时间最优轨迹，得到6 个关节各自的位置、速度、加速度以及力矩随时间变化曲线分别如图4—图7所示。

Fig.4 Joint position curve图4 关节位置曲线

Fig.5 Joint velocity curve图5 关节速度曲线

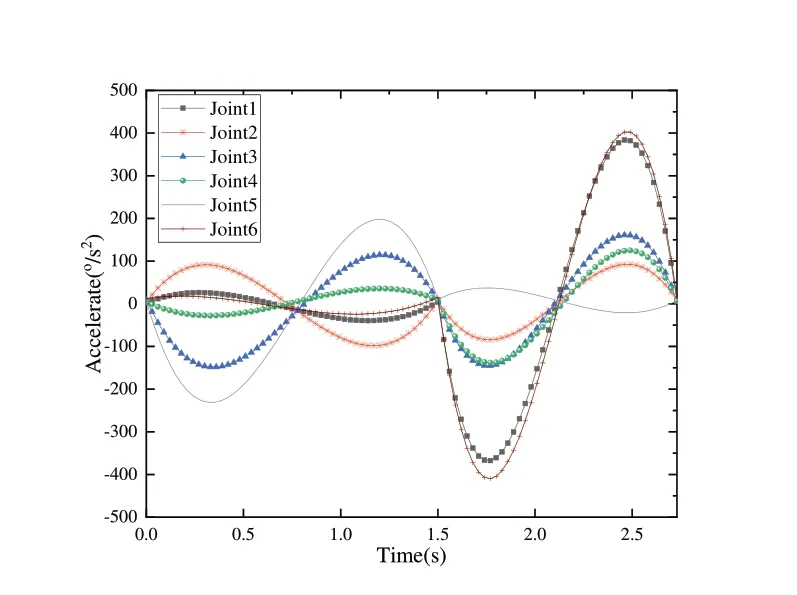
Fig.6 Joint acceleration curve图6 关节加速度曲线

从图4—图7 可知，所求出的运动时间都满足于机器人自身的运动学条件和动力学条件。从此条运行轨迹的约束条件上看，满足规划轨迹的主要约束界限为关节一的约束，特别是在1.5～2.7s 这一区间关节一运行加速度逼近的极限加速度，其他约束条件都有适当的缓冲区域可以调节，优化后从P1 到达P3 的时间为2.713 2s，而不使用优化算法从P1 到P3 的设定时间为3.8s，使用改进灰狼进化算法缩短了在相同条件之下到达目标点的时间，机器人效率提升28.6%。

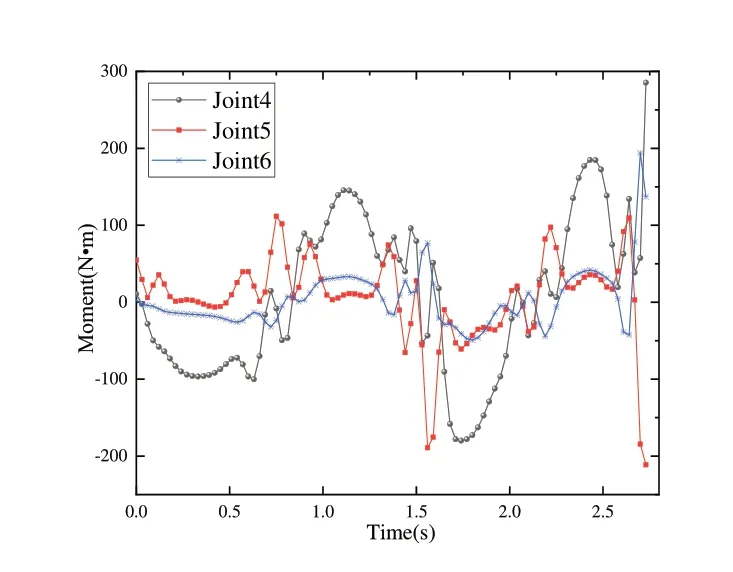
Fig.7 Joint torque curve图7 关节力矩曲线

5 结语

本文提出了一种轨迹规划方法，使用五次多项式对机器人关节角在满足机器人运动学及动力学约束情况下进行插补，并采用改进灰狼进化算法对机器人轨迹进行时间优化，获得符合条件的最优时间。试验结果表明，采用MDEGWO 算法比单独使用GWO 算法、DE 算法收敛速度更快，收敛精度更高；在保证关节位移、速度以及加速度平滑且符合动力学和运动学约束的条件下缩短了机器人到达同一目标点的时间，此方法比机器人默认的轨迹规划算法效率提高28.6%，为后续机器人控制研究提供了科学有效的理论依据。本文采用时间最优优化模型，后续将考虑机器人能量、冲击振动的多目标轨迹优化。此外，亦会考虑机器人动力学中关于电机和连杆间刚柔耦合因素的影响。