改进灰狼优化算法在炼钢过程中的应用

李晓宇，叶春明

（上海理工大学管理学院，上海 200093）

0 引言

灰狼优化算法是一种新型的群智能算法，2014 年由Mirjalili 等［1］根据狼群中的等级制度和捕食过程提出，被广泛运用于车间调度、参数优化及预测问题中。然而，该算法在后期容易陷入局部最优，无法获得最优解，这一点引起了学者们的关注。刘炼等［2］根据灰狼优化算法后期易陷入局部最优的特点，提出反向学习和基于精英狼群的醉汉漫步策略对其进行改进；黎素涵等［3］分析了非线性收敛因子和重选精英狼群对算法的影响；李阳等［4］提出一种分段可调节收敛因子，并对精英狼群采用莱维飞行和随机游走策略防止算法陷入局部最优；王梦璐等［5］提出动态反向搜索机制和sigmoid 函数改变线性收敛因子；徐松金等［6］基于遗传算子提出交叉变异机制，以提高算法的局部收敛能力和收敛速度。

钢铁制造业是工业生产的基础，有效的炼钢连铸调度方法可确保铁水准时运送到需要的工序，有利于减少能源消耗，降低碳排放。国内外学者针对炼钢连铸这一问题，从不同角度进行了研究。Kumar 等［7］采用组合拍卖方法，将炼钢调度问题转化成一个整数线性规划进行求解；韩大勇等［8］为提高炼钢连铸生产效率，以加权最大化完工时间和作业等待惩罚总和最小化为目标对炼钢连铸问题进行研究求解；Zarandi 等［9］通过建立混合整数线性规划模型，提出一种基于粒子群优化和模糊线性规划方法的组合求解炼钢连铸（SCC）调度问题；唐秋华等［10］将文化基因算法与启发式规则相结合，应用于炼钢连铸生产调度中；吴玲等［11］设计了两阶段方法求解多并行机多缓冲区的炼钢连铸生产调度，最后获得浇次的最优排序。

针对灰狼优化算法应用于混合流水车间调度这一问题，近年来很多学者开展了研究。如时维国等［12］提出改进参数C 的灰狼优化算法，求解加工阶段配置不均衡的混合流水车间；成舒凡等［13］利用改进的灰狼优化算法求解三阶段应急手术调度模型；张兴辉等［14］提出反向改进灰狼算法策略，以优化预测模型的超参数。

综上所述，目前国内外文献中，将灰狼优化算法应用于车间调度的研究有很多，但将其应用于炼钢连铸生产调度的很少。虽然有学者考虑钢铁加工过程中缓冲区的约束，但很少有学者考虑多并行机的加工问题。因此，本文首先对传统的灰狼优化算法进行改进，通过测试函数验证其性能的提升；然后建立多并行机带有缓冲区约束的炼钢连铸生产模型，并考虑钢铁加工过程中等待时间受限和最后一阶段无间断加工等特殊约束，将改进后的IGWO 运用于该模型中，验证算法和模型的有效性。

1 传统灰狼优化算法

根据灰狼在大自然中的捕 食行为，Mirjalili 等［1］在2014 年提出了灰狼优化算法。其将每一匹狼看作问题的一个解，求解精度最高的解被称为α 狼，求解精度次高的解为β 狼，求解精度第三高的解为δ 狼，剩下的狼群则为ω狼。ω 狼在α、β 和δ 狼的带领下不断更新自己与猎物的距离，无限接近猎物并进行抓捕、追踪、围猎和攻击。灰狼等级结构如图1所示。

Fig.1 Grey wolf hierarchy图1 灰狼等级结构

具体公式如下：

1.1 围猎猎物

式（1）表示个体与猎物之间的距离，式（2）为灰狼位置更新公式，式（3）、式（4）分别为系数向量更新公式。

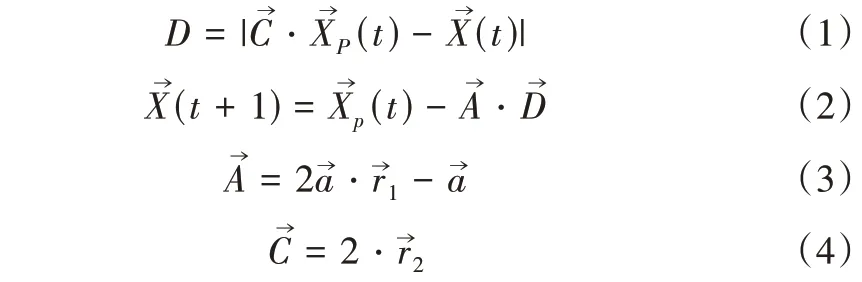
其中，t为目前迭代的次数分别表示猎物和灰狼的位置向量为系数向量为收敛因子。随着迭代次数从2线性减小到0是［0，1］范围内的随机数。

1.2 追捕猎物

根据种群中适应度前3 的狼群位置不断更新ω狼的位置，如式（5）-（7）所示。公式（8）表示ω狼的最终位置。

2 改进的灰狼优化算法

灰狼优化算法具有原理简单、参数较少、全局搜索能力强及易于实现等优点，因此被广泛应用于综合能源优化调度［15］、考虑云制造服务协同的多用户任务调度［16］、微电网经济优化调度［17］等领域。因为原始的GWO 算法存在后期全局搜索能力较差、易陷入局部最优以及收敛速度慢等问题，所以本文提出一种改进的灰狼优化算法（IGWO）。

2.1 基于反向学习的初始化种群

反向学习策略是一种智能计算方法，被广泛应用于各种智能算法中，包括GA、DE、BBO 和ACO 算法等。该策略通过生成反向解以增加种群的多样性，提高算法的寻优性能。因为种群初始化对于算法的搜索效率影响较大，所以本文采用反向搜索策略初始化灰狼种群。具体操作步骤如下：

（1）在搜索空间中随机初始化N 个灰狼xi，j(i=1，2，...，D；j=1，2，...，N)作为初始种群P，其中N 为灰狼个数，D 为空间维数。

（2）生成反向种群。需要每个灰狼个体生成其个体的反向点，假设在D 维空间上存在p=(x1，x2，...，xD)为其中的一个点，xi∈[li，ui]，i=1，2，...，D，则其反向点p'=，其中。随机产生的每个灰狼个体xi及其反向个体构成反向种群OP。

（3）将种群P 与OP 合并，在2N 个种群中选取适应度排序前N 的灰狼个体作为其初始种群。

2.2 非线性收敛因子

在灰狼优化算法中，当|A|＞1 时狼群进行全局搜索，|A|＜1 时搜索范围减小，即进行局部搜索。由式（3）可知，A 随着a 的变化而改变。传统的GWO 收敛因子a 随着迭代次数增加而线性递减，但算法的搜索是非线性变化的，收敛因子线性递减会导致算法后期的全局搜索能力较差，容易陷入局部最优［18］。因此，本文针对GWO 算法的迭代搜索过程，根据文献［3］，使用了非线性收敛因子。

非线性收敛因子随迭代次数的变化情况如图2 所示（彩图扫OSID 码可见，下同）。

Fig.2 Convergent factor variation图2 收敛因子变化

其中，直线表示传统GWO 算法收敛因子的变化情况，曲线表示改进后IGWO 算法收敛因子的变化情况。改进后的收敛因子呈抛物线形状，前期变化速率慢，可很好地适应种群的全局搜索能力；后期变化速率较快，有助于算法在局部搜索过程中快速、精确地找到最优解。本文采用的非线性收敛策略有利于平衡算法的全局搜索与局部搜索能力。

2.3 莱维飞行策略

在传统的GWO 算法中，随着a 的递减，|A|＜1 时狼群开始进行局部搜索，而后期群体中所有的个体均向α狼靠近，易出现早熟收敛的情况，陷入局部最优。本文针对这一问题，采用基于精英头狼的莱维（Lévy）飞行策略扩大后期精英狼α的搜素范围。

莱维飞行策略是服从莱维分布随机游走的一种方法，是一种短距离行走和较长距离行走相间的方式，因此莱维飞行具有良好的全局搜索能力。其位置更新公式如下：

式中，Xα(t)表示迭代到第t代时α狼个体的位置；⊕表示点对点乘法；b表示α狼个体的随机数，b=表示服从莱维分布的搜索路径，，其中λ的取值区间一般为1 ＜λ＜3，Xαbest表示历史最优解，μ和v服从的正态分布为

采用莱维飞行策略可更新灰狼位置，再采用贪心机制将原始解与新解的适应度进行对比，保留适应度更好的解。

2.4 算法步骤

改进后的IGWO 算法步骤如下：①进行参数设置：确定种群个数N、最大迭代次数Max_iter；②随机生成N 个种群，采用反向学习策略生成N 个反向解，合并排序并抽取适应度为前N 的灰狼种群，再将前3 个最优个体的位置依次保存为Xα、Xβ、Xδ；③根据式（1）-式（9）更新灰狼位置，并更新a、A、C 的值；④根据式（10）更新α 狼；⑤重复步骤③与步骤④，直至达到最大迭代次数，输出α 狼的适应度值，算法终止。

3 仿真实验

3.1 实验及数值分析

为测试改进后灰狼优化算法（IGWO）的性能，本文选取国际上常用的8 个标准测试集函数来验证算法，表1 列出了这些函数。其中，F1～F5 为单峰值函数，用于测试算法的局部搜索能力；F6～F8 为多峰值函数，用于测试算法的全局搜索能力。将改进的IGWO 算法与传统GWO 算法进行对比，为保证无偏性，设置迭代次数为500。为排除偶然性，所有实验均独立运行30 次，记录实验的平均值和标准差来衡量算法性能。

本文实验环境为：系统Windows 10，512G 固态硬盘，INTEL 酷睿I5-1135G7 的CPU 和内存为16GB 的PC 机，所有算法均使用MATLAB2016版本完成。

3.2 实验结果与分析

表2 是30 维下两种算法测试结果的平均值和标准差，可以看出，不管是平均值还是标准差，改进后的IGWO 算法较改进前求解精度更高。尤其是从函数F1、F2、F3、F4、F7 可以看出，IGWO 算法的求解精度明显高于GWO 算法，而对于函数F5、F6、F8，IGWO 算法的求解精度略高于GWO 算法。仿真实验结果显示了改进IGWO 算法的有效性。

为更直观地表现改进前后GWO 算法的收敛情况，图3给出了30 维下针对F1-F4 4 个函数两种算法的收敛曲线。从图中可以看出，算法在迭代前期的收敛情况基本一致，而在迭代后期，改进后IGWO 算法的收敛速度、收敛精度相较于GWO 算法都表现更好。

Table 1 Eight standard test functions表1 8个标准测试函数

Table 2 Comparison of GWO and IGWO on 8 standard test functions表2 GWO算法与IGWO算法针对8个标准测试函数对比

4 多缓冲区多并行机的炼钢连铸生产调度问题

4.1 问题描述

炼钢连铸生产过程主要分为3 个阶段：炼钢（EAF）—精炼（AOD）—连铸（CC）。由于实际炼钢过程中等待时间受限，本文考虑了3 种不同类型的缓冲区，并利用两阶段的方法求解浇次序列。通过使用缓冲区压缩规则以提高机器利用率、减少空转时间，从而减少机器空转的能耗时间。钢铁生产流程（加缓冲区）如图4所示。

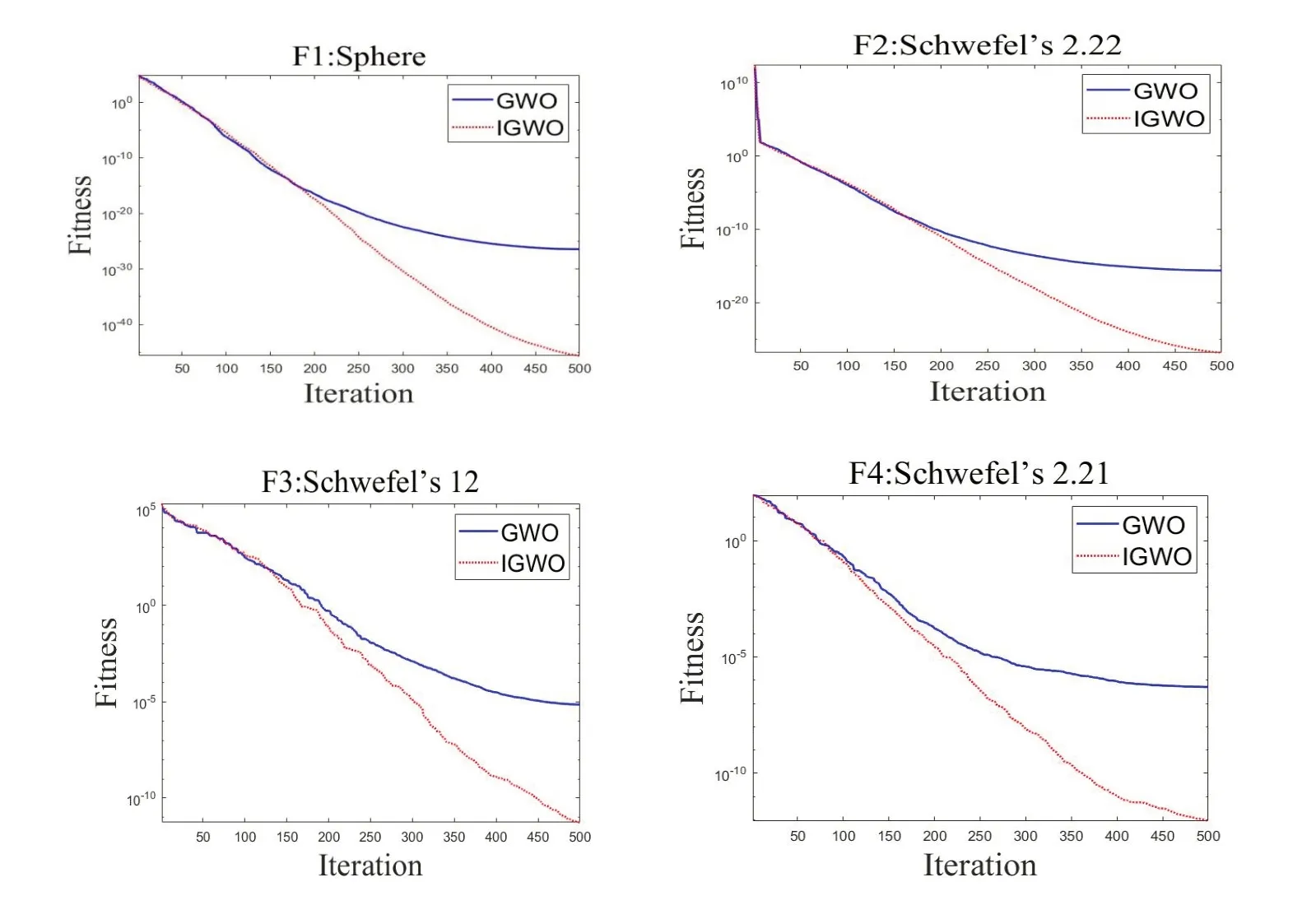
Fig.3 Convergence curves of the two algorithms for solving F1-F4 functions图3 两种算法求解F1-F4函数的收敛曲线

Fig.4 Steel production process（plus buffer）图4 钢铁生产流程（加缓冲区）

本文以某钢厂的工艺流程为例，利用IGWO 算法求解炼钢连铸生产调度问题。共选取10 个待加工浇次，每个浇次包含不同数量的炉次，在不同类型及不同数量缓冲区的约束下，按照同一个工艺路线（即EAF-AOD-LF1-LF2-CC）进行加工。考虑缓冲区的炼钢连铸已有学者研究过，但本文考虑的是多缓冲区多并行机的加工问题，该领域很少有学者研究。

本文将缓冲区看作加工时间为0 的生产阶段，于是可将求解问题抽象为含有特殊约束的7 阶段混合流水车间调度求解最大完工时间，属于规模大、约束多、强耦合的NP-hard 问题［19］。

4.2 炼钢连铸数学模型

4.2.1 参数设置

具体参数设置如下：

L：炉次集合，L=｛1，2，3，...，l，...，|L|｝，其中|L|为炉次总数。

J：浇次集合，J=｛1，2，3，...，j，...，|J|｝，其中|J|为浇次总数。

S：生产阶段集合，S=｛1，2，3，...，s，...，|S|｝，其中|S|为生产阶段总数，本文的|S|=7。

K：炉次事件集合，K=｛1，2，3，...，k，...，|L|｝。

I：浇次事件集合，I=｛1，2，3，...，i，...，|J|｝。

NJ：浇次J包含的炉次总数。

LJ：浇次J包含的炉次集合。

MS：S 阶段包含的机器数量，M_S=｛1，2，3，...，m，...，|M_S|｝，其中|M_S|为S阶段包含的机器总数。

tk，s，m：炉次K 在S 阶段m 台机器上处理一炉的时间，其中，S∈［1，7］。

P：相邻浇次间的准备时间（相邻浇次J 在连铸阶段的预留准备时间），设置为60。

r：有限缓冲区允许炉次停留的最大时间，超过该时间将影响工件质量。

决策变量如下：

xj，i：0-1 变量，当浇次j 分配到浇次事件点i 时等于1，否则为0。

yl，k：0-1 变量，当炉次l 分配到炉次事件点k 时等于1，否则为0。

qk，s，m：0-1 变量，当炉次事件点k 在阶段S 分配到机器m 上时等于1，否则为0。

bk，s：连续变量，表示炉次事件点k_ 在阶段S_ 的开始时间。

ck，s：连续变量，表示炉次事件k在阶段S的结束时间。

H：足够大的常数。

4.2.2 问题假设

本文考虑在满足炼钢连铸工艺一般性约束中加入特殊性约束，以优化最大完工时间，使得研究问题更接近实际生产情况。为构建合理的模型，实验需要满足以下假设条件：①每台机器在工作过程中不会出现故障；②各机器在任一时刻最多只能加工一个炉次；③各阶段的炉次连续加工；④同一阶段并行机加工同一炉次的时间一致；⑤使用同一台连铸机的，必须考虑相邻浇次间更换中间包的准备时间；⑥不考虑因温度降低导致的重调度问题；⑦在不具备加工能力的阶段（即炉次属于缓冲区阶段），各炉次最多只能分配到一个缓冲区上。

4.2.3 数学模型

目标函数如下：

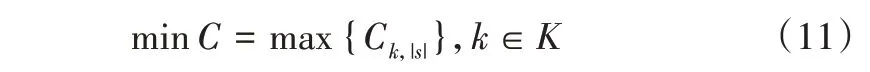
一般性约束条件如下：

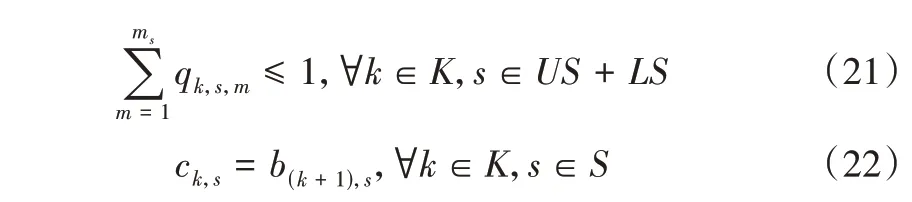
其中，式（11）为目标函数，表示最小化最大完工时间；式（12）表示浇次与加工次序间存在对应关系；式（13）确定了浇次中的炉次序列；式（14）表示同一浇次内的炉次在连铸阶段，需在同一台机器上不间断地加工；式（15）表示任何时候一台机器只能加工一个炉次；式（16）表示炉次在s个阶段连续进行加工；式（17）表示使用同一台连铸机器的浇次，必须考虑相邻浇次间更换中间包的准备时间；式（18）表示在缓冲区阶段，缓冲区具有缓存能力；式（19）表示在前两个缓冲区，缓存时间是无限的；式（20）定义了有限缓冲区开始到结束之间的关系，以及缓冲区存储的时间上限；式（21）定义了在不具备加工能力的阶段，各炉次最多只能被分配到一个缓冲区上；式（22）表示炉次间连续工作。

5 基于IGWO的炼钢连铸调度求解

目前灰狼优化算法已在很多工业领域有了成功应用。本文将以炼钢连铸生产调度问题为例，采用IGWO 算法求解最大完工时间，结合启发式规则求解浇次内和浇次间的排产顺序，从而获得最小化最大完工时间。

5.1 浇次内与浇次间启发式规则

对于浇次内的炉次，要求最后一阶段在同一台机器上不间断地进行加工，故本文采用回溯倒排法，即最后一道工序成为第一道工序。获得最大完工时间后进行正序，即将最大完工时间减去当前求得的工件开始和结束时间，获得工件调度的具体时间。由于正序后的加工时间间隔大，生产过程不紧凑，于是利用缓冲区储存工件并进行压缩，以确保炉次（工件）的连续加工，减少设备空转时间。

对于浇次间的排序，需要考虑最后一阶段更换中间包的时间。若相邻浇次最后一阶段在同一台机器上加工，则需要考虑更换中间包的时间；若相邻浇次最后一阶段不在同一台机器上加工，只需将后一浇次信息追加到当前调度方案之后，把整块信息往前推，直到第一台设备出现冲突。并且为了满足工序之间无等待的约束，浇次间利用缓冲区进行调整。

5.2 编码

由于灰狼优化算法适合解决连续解空间中的问题，而炼钢连铸生产调度是连续和离散相混合的复杂生产过程，为了让IGWO 算法更好地解决此类HFSP 问题，本文以浇次为最小单位，采用浇次序列进行编码，将离散的解空间连续化。通过把每一个浇次看作（0，2）之间的实数，该浇次对应序列是向量中数值的大小，例如5 个浇次对应的向量编码为（1.23，0.84，1.35，0.33，0.98），则浇次的加工顺序为（2，4，1，5，3）。数值代表浇次序号，编码长度|J|表示待调度的浇次总数。

5.3 解码

由于炼钢连铸过程的特殊约束，本文将采用逆序解码策略。首先，结合浇次内的启发式规则对浇次内的炉次进行排产，确定各浇次内炉次在不同工序上的加工时间和结束时间；然后，在当前浇次未断浇时仍然继续炉次的排产，直至开始下一个浇次；接下来对浇次内的炉次进行定时，并将整体置于现有的调度计划之后，结合浇次间的启发式规则进行解码，最终可获得最大完工时间（适应度值）。

5.4 嵌入变邻域搜索策略

常见的变领域搜索结构有交换、插入和逆序。为了增强算法的局部搜索能力，对于IGWO 算法嵌入变邻域搜索进行求解。本文根据求解问题的特点，采用互换的邻域结构进行变邻域搜索。

5.5 实验仿真与分析

为验证模型和算法的有效性，本文根据文献［20］随机选取10 个浇次进行实验，并利用传统的GWO 算法进行对比实验。算例的相关设置为：生产阶段|S|=7，各阶段加工机器数量如表3所示。

Table 3 Number of processing machines at each stage表3 各阶段加工机器数量

待调度浇次总数|J|=10，每个浇次包含的炉次数NJ∈[1，7]，各个浇次在第7 阶段的准备时间P=60min，各炉次在各阶段的加工时间如表4所示。

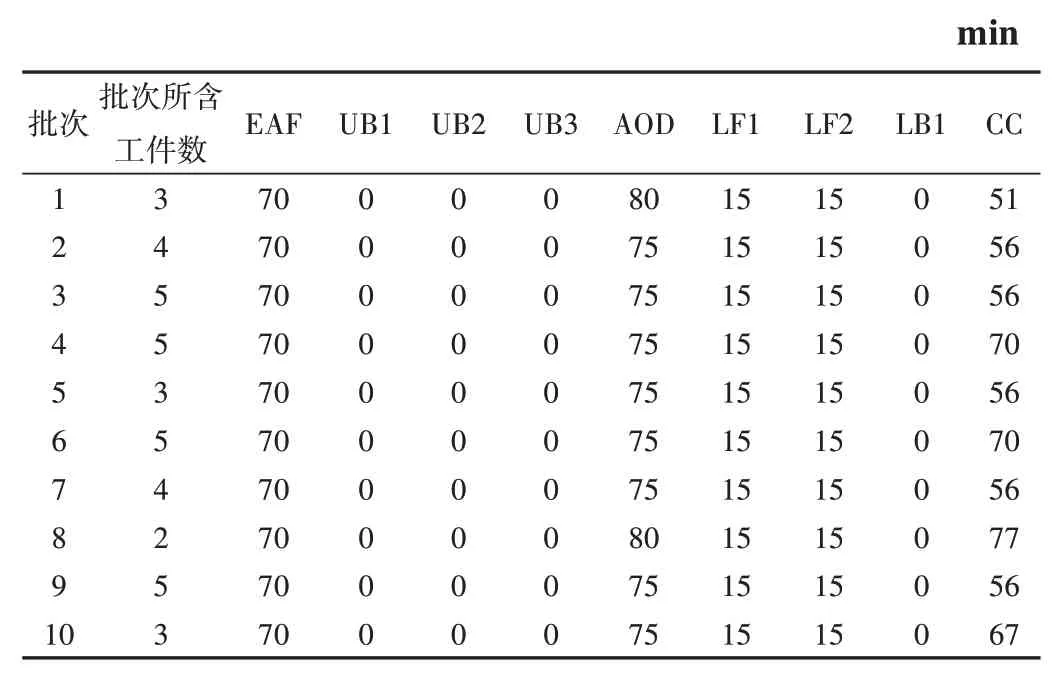
Table 4 Processing time of each stage表4 各阶段加工时间

统一设置种群规模为50，迭代次数为500，采用本文改进的IGWO 算法和传统GWO 算法求解最大完工时间。

5.6 实验结果分析

通过随机选取浇次进行实验分析，验证算法的有效性，本文选取10 个浇次数的炼钢连铸生产数据进行实验。为防止因偶然性出现的偏差，分别对两组实验独立运行20次，并求平均值。算法运行结果如表5 所示。本文实验环境为：系统Windows 10，512G 固态硬盘，INTEL 酷睿I5-1135G7 的CPU，内存为16GB 的PC 机，所有算法均使用MATLAB2016版本完成。

Table 5 Running result of the algorithm表5 算法运行结果

从表5 可以看出，改进后IGWO 算法的求解精度优于传统的GWO 算法，证明改进的灰狼优化算法相较于传统算法可跳出局部最优，获得更优的值。

为了更好地显示算法的收敛速度，本文选取第14 次的运行结果绘制两种算法的收敛曲线，如图5所示。

Fig.5 Algorithm optimization process图5 算法寻优过程

为更清晰地呈现出浇次间和浇次内的排产情况，图6选取浇次排产序列中相邻3 个浇次的调度顺序。图7 表示3 个相邻浇次中浇次2 的排产情况，可看出该调度方法明显提升了设备利用率，生产过程变得更紧凑，浇次在EAF和AOD 阶段的完成时间减少，减少了机器的空转时间，从而减少了机器空转产生的碳排放。

Fig.6 Production layout diagram of adjacent casting process图6 相邻浇次加工排产图

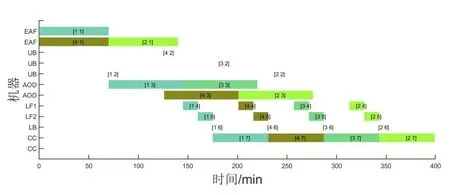
Fig.7 Production scheduling of the 2th casting time图7 浇次2排产情况

6 结语

本文研究了利用改进的灰狼优化算法求解炼钢连铸生产调度问题，结合实际生产情况，在缓冲区的约束下建立炼钢连铸生产调度模型，并根据求解问题的特点对改进的灰狼算法引入变邻域搜索策略，结合启发式的解码规则求解炼钢连铸过程中的最大完工时间，通过合理的排产顺序可提高设备利用率。最后通过算例进行模拟实验，将改进的灰狼优化算法与传统灰狼优化算法寻优过程所求结果进行对比，结果表明，改进的灰狼优化算法在求解炼钢连铸调度上有较大优势。

本文建立的炼钢连铸生产调度模型可减少机器等待时间、提高设备利用率，但没有用数据和实验证明改变调度方案对于炼钢连铸过程中所排放二氧化碳的减少情况。接下来将结合机器空转、工件等待散热以及工件加工过程中的二氧化碳排放情况，研究采用何种方法可大幅减少碳排放量，并研究在碳限额政策下如何在保证低碳生产的同时降低经济成本的问题。