基于IGWO-SVM的基桩缺陷分类识别

李天博，任 昊，董德勇

（1.江苏大学电气信息工程学院，江苏镇江 212013；2.国网江苏省电力有限公司检修分公司，江苏南京 210000）

0 引言

目前，针对基桩的完整性检测多采用超声透射法与钻芯法相结合的方式［1-2］，其中超声透射法中获得的超声波信号包含很多声学参数信息，如声时、波幅、频率和能量等。具体步骤为采用相敏检测（Phase-sensitive Detection，PSD）判据结合声时、波速、首波幅值分析基桩缺陷，然后通过平测法与斜侧法相结合实现对缺陷位置区域的预估，最后通过钻芯法确定缺陷类型［3］。然而钻芯法是一种有损检测，会破坏桩身结构完整性，因此目前许多学者开始尝试采用机器学习的方式识别基桩缺陷类型。

采用机器学习方法实现对基桩缺陷类型的识别首先要对超声信号进行特征提取，再根据提取的特征参数建立分类模型。常用超声信号特征提取方法包括基于时域、频域以及小波包分解（Wavelet Packet Decomposition，WPD）的方法。例如，文献［4］从超声信号的时域和频域特征方面进行分析研究，实现了基桩缺陷的分类；文献［5］提出一种基于小波包能量比的特征提取方法，通过支持向量机（Support Vector Machine，SVM）实现了对基桩缺陷的分类；文献［6］将小波分析与神经网络相结合，使用极值点的小波分析作为神经网络输入，实现了对基桩缺陷类型的识别。然而单一尺度的特征提取往往不够全面，会丢失部分重要特征信息，需要对不同尺度提取的特征进行融合，丰富不同类型基桩缺陷的超声信号信息。

应用于基桩缺陷分类识别的常见算法模型包括BP（Back Propagation）神经网络［7］、K 近邻（k-Nearest Neighbor，KNN）［8］和SVM［9］，其中BP 神经网络对于小样本的分类会出现过拟合现象且泛化能力不佳；K 近邻算法在样本不平衡时对稀有类别的预测准确率低；SVM 具有很好的泛化能力，适用小样本分类，且实现简单，具有较好的鲁棒性。例如文献［10］采用小波包与SVM 实现了对桩身缺陷严重程度的识别；文献［11］采用小波分析和SVM 实现了基于超声透射法的基桩缺陷类型识别。然而，正则化系数C和核参数g 的选择对SVM 的分类效果有很大影响。为提高分类准确率，使用优化算法对该参数进行寻优已成为主流，常用优化算法包括粒子群优化算法［12］（Particle Swarm Optimization，PSO）、萤火虫算法［13］（Firefly Algorithm，FA）、灰狼优化算法［14］（Grey Wolf Optimizer，GWO）。例如，文献［15］通过改进非线性控制因子提高GWO 算法的收敛精度与稳定性，通过经验模态分解提取特征参数，然后采用改进GWO 算法优化SVM 分类模型，最终实现了对风力机齿轮故障类型的诊断。GWO 算法虽然参数少、易于实现，但容易陷入局部最优，且后期寻优能力不足。

基于以上分析，本文提出融合时域、频域与小波包能量的特征提取方法，并针对GWO 算法易陷入局部最优且收敛速度慢的问题对其进行改进，采用Sobol 序列初始化灰狼种群并引入莫兰指数，提高了GWO 算法的全局收敛能力，最终建立了基于改进灰狼优化算法—支持向量机（Improved Grey Wolf Optimization-Support Vector Machine，IGWO-SVM）的分类模型，实现了对基桩缺陷类别的高精度识别。

1 特征提取

1.1 时域特征

时域特征是以时间为变量衡量信号特征的重要指标，包括量纲特征参数和无量纲特征参数。由于混凝土基桩结构的复杂性和不确定性会对波形造成很大影响，本文在时域特征参数方面主要针对超声信号的首波进行提取，在量纲参数方面主要包括声速、首波幅值与峰值，在无量纲参数方面主要包括波形因子、峰值因子、脉冲因子、裕度因子以及余隙因子［16］。

1.2 频域特征

与时域特征相比，频域特征虽然没有那么直观，但却更加简洁，且频域信息可以弥补一些时域信息无法体现的超声信号。本文对时域信号进行傅里叶变换得到超声信号的频域波形，提取到重心频率、平均频率、均方根频率、频率标准差4个频域特征参数［16］。

1.3 小波包能量特征

为避免时域、频域特征参数作为分类模型输入过于单一的问题，本文在特征提取方面加用小波包变换法。小波包变换在分解低频部分的同时对高频部分也进行了分解，这种分解不仅没有冗余，而且不会出现疏漏，能够对包含大量中、高频信息的信号进行更好的时频局部化分析。小波基函数的选择会对数据处理造成一定影响，常用小波基函数包括哈尔小波（Haar）［17］、紧支集正交小波（Daubechies，dbN）［18］、近似对称的紧支集正交小波（Symlet，symN）［19］。其中Haar 小波是支撑域t ∈[0，1]范围内的单个矩形波，在时域上不是连续的，因此作为基本小波的性能不是很好。而symN 小波是对dbN 小波的一种改进，其在连续性、支集长度、滤波器长度等方面与dbN 小波一致，但symN 小波具有更好的对称性，即能在一定程度上减少对信号进行分析和重构时产生的相位失真。因此，本文选用symN 小波作为小波基函数，其中阶数N设为6，小波分解层次为5 层，计算前8 个子频带的能量占比作为特征值，公式为：

式中，Ei表示第i个子频带的能量。

2 缺陷识别模型

2.1 SVM

SVM 多用于二元分类，对于多元分类则需将其拆分为多个二元分类问题［8］。目前SVM 多元分类方法主要包括成对分类方法（One-against-one）、一类对余类（Oneagainst-all）以及二叉树。本文采用成对分类方法，其在每两个类之间都构造了一个分类平面。

SVM 的决策函数表示为：

常用核函数包括线性核、多项式核、高斯核、Sigmoid核等，考虑到本文研究对象的特殊性以及核函数参数优化的难易程度，选择高斯核［20］作为核函数，表示为：

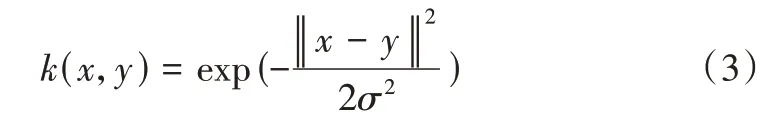
SVM 中惩罚因子C以及核函数参数g的选取会直接影响模型的分类准确度。智能优化算法目前已成为筛选最优参数的主流方法，其中GWO 算法具有参数少、易于实现、局部寻优能力强等优点，因此本文采用GWO 算法对SVM 进行参数寻优，并与IGWO 算法进行比较。

2.2 IGWO算法

2.2.1 基于Sobol序列的种群初始化

原始GWO 算法的种群初始化是随机产生的［14］，在很大程度上影响了算法的寻优性能。而Sobol 序列［21］不仅可以使空间点均匀分布，而且不需要预先确定样本数量并对其进行存储，可根据需要生成无限个样本。因此，本文引入Sobol 序列，实现对灰狼种群初始化位置的筛选，提高灰狼种群的均匀性和多样性，进而提高原始GWO 算法的寻优性能。

Sobol 序列的每一个维度均为以2 为底数的Radical inversion，每个维度有不同的生成矩阵C，当C取单位向量时，对应的Sobol序列表示为：

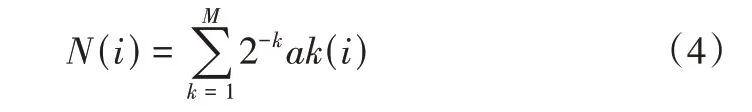
将i表示为二进制的数，数中每一位上的ak(i)排成一个向量，将其镜像到小数点右边转换成十进制，由此可以得出一维Sobol 序列Xi={N(1)，N(2)...，N(i)，i∈N}，多维Sobol 序列则通过乘以每个维度的生成矩阵C得到。在目标参数寻优的阈值内采用Sobol序列均匀分布n个点，作为初始化种群空间位置，其中前3个解分别定义为α、β、δ狼。

2.2.2 引入莫兰指数

原始GWO 算法通过判断|A|是否大于1 实现狼群对目标的追捕或放弃追捕，从而避免陷入局部最优。A值的大小取决于收敛因子a和随机值r1，其中收敛因子a是随着迭代次数的不断增加从2 线性减小到0 的；随机值r1一定程度上限制了算法的灵活性，不能有效跳出局部最优。为此，本文引入莫兰指数［22］干预r1取值，以提高GWO 算法的全局搜索能力。莫兰指数作为空间自相关系数的一种，其值分布在[ -1，1]之间，用于判断一定范围内的空间实体是否存在相关性。

空间自相关的莫兰指数可表示为：

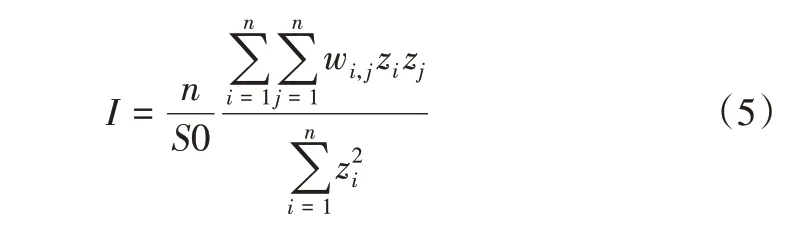
式中，z为要素i、j属性与其平均值的偏差，wi，j为要素i和j之间的空间权重，n为要素总数；S0为所有空间权重的聚合，表示为：

式中，i为灰狼个体的适应度，j为灰狼个体与猎物Xp(t)的欧式距离，n为种群数量。

空间权重矩阵采用距离标准衡量，本文的距离标准为个体狼之间欧式距离平方的倒数，表示为：

通过莫兰指数的I值判断当前灰狼种群是否处于局部最优状态，以I值为限制条件干扰随机值r1的取值范围。通过多次计算得出当I值约为0.12 时会陷入局部最优状态，此时需要对狼群下达放弃猎物的命令从而放弃当前最优。判断公式为：

式中，M为最大迭代次数，t为当前迭代次数。由I值决定r1的取值范围，间接影响|A|值从而及时跳出局部最优。当I值≤0 时，狼群处于自由分布或与α狼成负相关状态，此时解除放弃猎物命令，r1取值重新恢复到[0，1]。由于种群可随机分布，本文不作原假设。

2.3 基于IGWO-SVM 的分类模型

基于IGWO-SVM 的模型分类流程见图1。

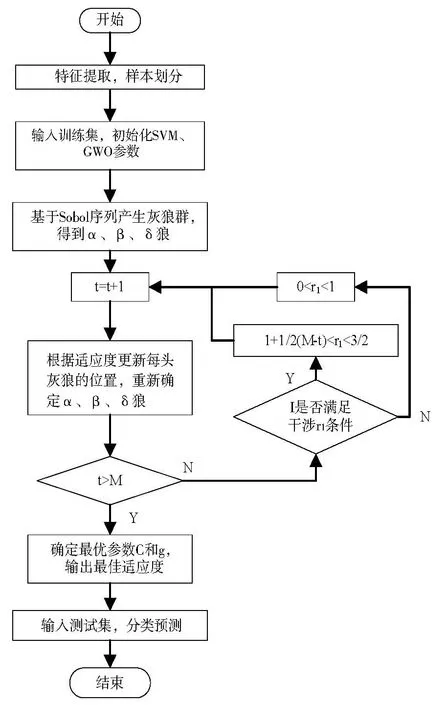
Fig.1 IGWO-SVM model flow图1 IGWO-SVM 模型流程

基于IGWO-SVM 的分类模型算法步骤为：①对超声信号进行时域、频域和小波包的融合特征提取；②划分数据集划分，初始化SVM 分类模型参数；③采用Sobol 序列对灰狼种群初始化，取前n个适应度作为灰狼种群规模，前3个适应度个体分别对应α、β、δ狼，初始化最大迭代次数M，收敛因子a和协同系数A、C；④迭代次数t=t+1；⑤更新种群个体位置；⑥根据适应度更新α、β、δ狼的个体位置；⑦判断当前迭代次数是否达到最大迭代次数M，达到则停止搜索，否则执行步骤5；⑧计算当前I值，判断是否达到0.12，若达到，则下达放弃猎物指令（更改r1取值范围）然后执行步骤2，持续到I值≤0 或头狼位置更新到更优解时撤销放弃猎物指令（r1取值范围恢复到［0，1］），否则执行步骤2；⑨输出最优解；⑩确定最优模型，实现缺陷分类识别；⑪输出各类型缺陷识别准确率。

3 实验结果与分析

3.1 数据处理

实验使用的超声检测仪器采样率为1.25MHz，主频为60KHz，每段波形采样512 个点。采集5 组波形，分别为正常、离析、夹泥、空洞、断桩。基桩声测管间距分别为0.6m、0.7m、0.8m，基桩强度等级均为C35，声测管内耦合剂均为清水。样本划分情况见表1。

图2 为正常基桩0.6m 测距剖面某一深度的超声信号，其中图2（a）为超声信号的时域波形，t0点的横坐标表示超声信号从发射到接收所需要的时间，即声时，由此可以计算出该测面对应深度的声速，而t1点的纵坐标则为首波幅值。图2（b）为超声信号的频域波形，可以看出超声信号对应主频为45KHz 左右，但高频信号达到100KHz，因此需要对时域波形进行低通滤波，截止频率设置为60KHz。

Table 1 Sample division information表1 样本划分情况

Fig.2 Normal foundation pile 0.6m ranging ultrasonic signal图2 正常基桩0.6m测距超声信号

对超声信号进行预处理后采用本文方法对不同基桩缺陷类型数据分别提取7 维时域特征，包括声速、首波幅值、波形因子、峰值因子、脉冲因子、裕度因子和余隙因子，以及4 维频域特征，包括重心频率、平均频率、均方根频率和频率标准差［16］。图3 为不同缺陷类型的超声信号经过小波包5 层分解后的能量占比情况，从（a）到（e）分别对应正常、离析、夹泥、空洞、断桩5 种类型不同子频带的能量占比情况。可以看出，能量基本集中在前8 个子频带，因此提取前8 个能量占比数据作为小波包特征，结合时域的7 维特征以及频域的4 维特征，每组信号样本特征维度为19，样本按照4∶1的比例分为训练集和测试集。

3.2 模型性能分析

采用IGWO 算法对SVM 分类模型进行优化，试验使用留一法，其中正则化系数C的取值范围为［0.0001，100］，核参数g的取值范围为［0，10］［23］。对165组测试集分类结果建立混淆矩阵，结果如图4 所示，可以看出IGWO-SVM 模型分类识别整体准确率可达96.97%。

为进一步确定本文模型的有效性，采用精准率（Precision）、召回率（Recall）、F1 值（F1-score）3 个指标对其进行评价［24］，计算方式分别为：

式中，TP表示待识别类型的实际类别与预测类别吻合的数量，FP表示识别错误对应预测类别的数量，FN表示识别错误对应实际类别的数量。本文模型对5 种基桩缺陷类型的识别精准率（Precision）、召回率（Recall）、F1 值（F1-score）如表2 所示。可以看出，除离析类型的精确率为87.5%外，其余各类别各项指标均高于90%，其中断桩的各指标均为100%，说明本文模型具有较好的基桩缺陷分类识别性能。

3.3 与其他模型比较

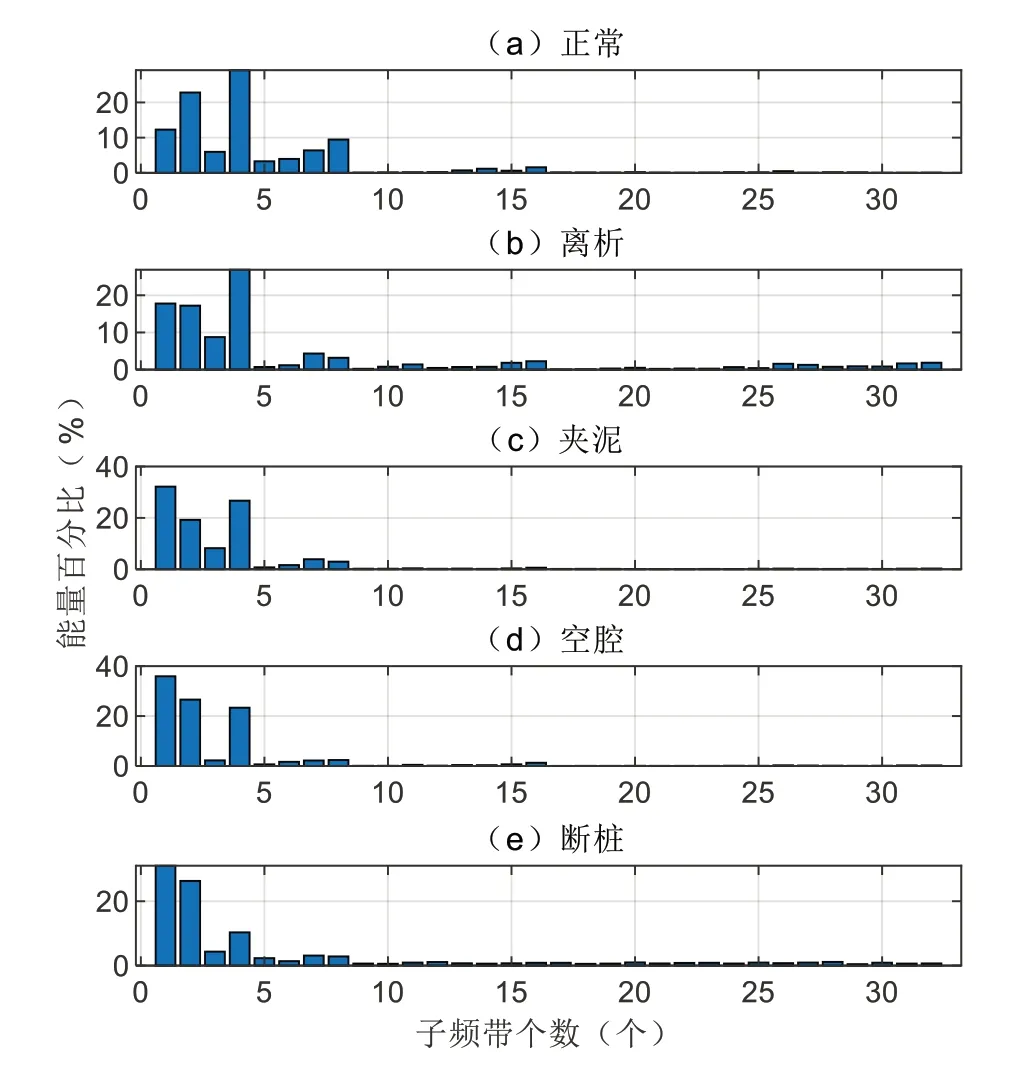
Fig.3 Wavelet packet energy ratio of different defect types图3 不同缺陷类型小波包能量占比

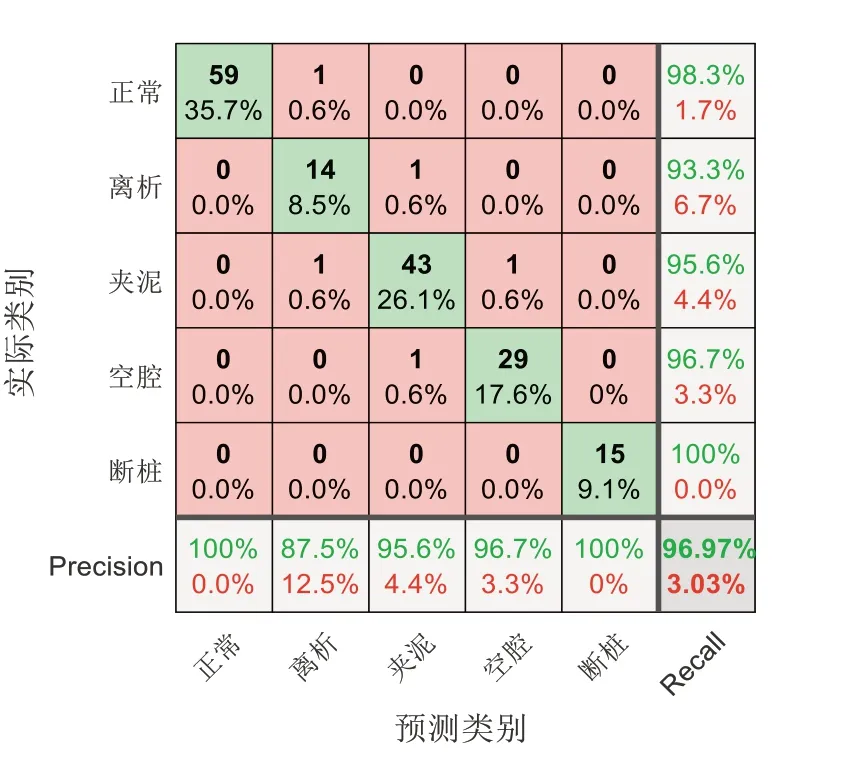
Fig.4 Confusion matrix of defect type recognition results图4 缺陷类型识别结果的混淆矩阵

Table 2 Calculation results of each index of the model表2 模型各指标计算结果 （%)

针对GWO 算法收敛速度慢以及易陷入局部最优的缺点，本文采用Sobol 序列初始化灰狼种群并引入莫兰指数干预r1的取值范围以改进GWO 算法。为验证改进GWO算法的有效性和优越性，对两处改进进行消融实验，种群数量设置为20，迭代次数为60 次，结果见表3 和图5。其中SGWO-SVM 为采用Sobol 序列初始化灰狼种群改进GWO 算法后优化的SVM 分类模型，MGWO-SVM 为引入莫兰指数后的GWO 算法优化的SVM 分类模型，GWO-SVM为原始GWO 算法优化的SVM 分类模型。可以看出，SGWO-SVM 的最佳适应度虽然在一开始低于GWO-SVM和MGWO-SVM，但由于其采用了Sobol 序列初始化灰狼种群，使得种群具有多样性，从第5 次迭代开始，其最佳适应度便高于GWO-SVM 和MGWO-SVM，收敛速度明显提高。相较于SGWO-SVM 和GWO-SVM，SGWO-SVM 采用莫兰指数干预r1的取值范围，使其在迭代57 次时跳出局部最优而得到全局最优解。结合了两项改进的IGWO-SVM 仅在迭代28 次时便得到全局最优解，在全局收敛能力方面明显提升。

Table 3 Ablation experiment results表3 消融实验结果

Fig.5 Ablation experiment results图5 消融实验结果

分别采用IGWO 算法、GWO 算法、FA 算法、PSO 算法对SVM 分类模型进行参数阈值寻优，各优化算法的种群数量均为20 个，迭代次数均为50 次，优化结果见表4 和图6。可以看出，IGWO 算法由于采用了Sobol 序列初始化灰狼种群，并引入了莫兰指数，在最佳适应度以及收敛速度方面均优于其他优化算法，在迭代28 次时便获得模型最佳适应度，为96.97%。

Table 4 Optimization results of SVM parameters by different optimization algorithms表4 不同优化算法对SVM参数的优化结果

分别采用时域特征提取、频域特征提取、小波包能量特征提取以及融合特征提取作为分类模型的输入，选择BP 神经网络、KNN 模型与SVM 分类模型进行比较，结果如表5 所示。可以看出，SVM 分类模型在以不同特征提取方法作为模型输入的情况下，识别准确率均高于相同条件下的其他分类模型。融合特征提取方法作为不同分类模型的输入，整体识别效果明显优于其他单一特征提取方法，其中融合特征提取方法结合SVM 分类模型对基桩缺陷的识别准确率可达96.97%，比BP 神经网络、KNN 模型分别高出6.36%、12.36%。

Fig.6 Optimal fitness curve of different optimization algorithms图6 不同优化算法的最佳适应度曲线

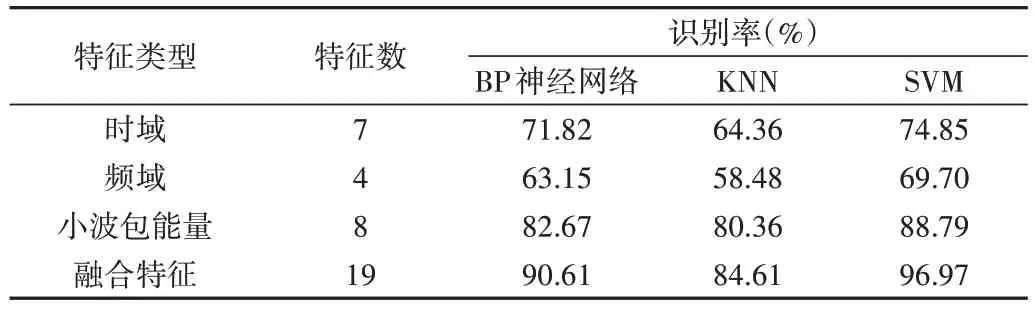
Table 5 Identification results of foundation pile defects by different classification models表5 不同分类模型对基桩缺陷的识别结果

4 结语

为提高基桩缺陷分类识别精度，本文提出融合特征提取方法，将时域特征、频域特征与小波包能量特征作为分类模型输入，并采用Sobol 序列初始化灰狼种群和引用莫兰指数干预r1取值范围的方法改进GWO 算法，提高了其全局收敛能力，然后采用该改进GWO 算法对SVM 分类模型进行参数寻优，最终建立了IGWO-SVM 分类模型。试验结果表明，本文方法能够实现对基桩缺陷的高精度识别。由于基桩内部结构复杂性较高，获取更多类型的样本数据以进一步提高分类模型的识别精度和泛化性将会是后续重点研究方向。