ZPW-2000A轨道电路故障诊断方法研究

王钟锐，李 鹏，陈光武

（1.甘肃省高原交通信息工程及控制重点实验室；2.兰州交通大学自动化与电气工程学院，甘肃兰州 730070）

0 引言

近年来，随着我国铁路的飞速发展以及各种用于提速与提高运输效率的新技术的推广，轨道电路作为检测列车位置的重要装置，其自身的运行状况直接影响着列车运行状态，因此在保障铁路运行安全与提高运输效率过程中起着至关重要的作用［1］。为保证其能够正常运行，铁路单位每年对其运行维护投入的成本也越来越多。因此，研究轨道电路的故障诊断与预测技术，实现精确运维与早期故障预警，从而顺应铁总所倡导的从“故障修”转为“状态修”的转变，具有重要的理论意义和实用价值［2］。

现阶段在铁路中应用的轨道电路有多种类型，其中交流轨道电路最为常见，包括50Hz 相敏轨道电路、ZPW-2000A 系列无绝缘轨道电路等，后者在高速铁路中发挥了重要作用［3］。据国家统计网的数据显示，截至2021 年末，全国铁路营业里程达到150 000km，其中高铁营业里程达到40 000km。铁路复线率为59.5%，铁路电化率为73.3%。全国铁路路网密度达到156.7km/万km2，ZPW-2000A 系列轨道电路覆盖率达到95.5%。因此，本文主要对ZPW-2000A 系列的轨道电路故障诊断方法进行综述。

1 现阶段故障诊断主流路线

ZPW-2000A 系列轨道电路故障信号主要表现为集中监测系统中轨道状态显示异常以及轨道检测车采集到的数据异常，其中轨道检测车采集数据的表现形式有多种，如感应电压与感应电流、补偿电容及载频信息等。

现阶段的轨道检测车以高速动车组为载体，可编入正常运营图运行，一方面不影响高速铁路的正常运行秩序，可提高检测频率；另一方面由于车体、速度与实际运营条件接近，获取的检测数据能真实反映列车和基础设施运营时的状态。轨道检测车可根据车上感应线圈通过无绝缘轨道电路时产生的电磁感应，得到与该轨道电路相对应的感应电流及感应电压等信息［4］。

铁路信号集中监测系统在轨道电路方面的监测内容主要包括发送器故障、接收器故障以及两端的调谐匹配单元故障等，上述故障均表现为多维形式，包括数字量、模拟量以及对应设备正常与否的开关量［5］。目前主流的以上述故障信息为基础的无绝缘轨道电路检测方法技术路线如图1所示。

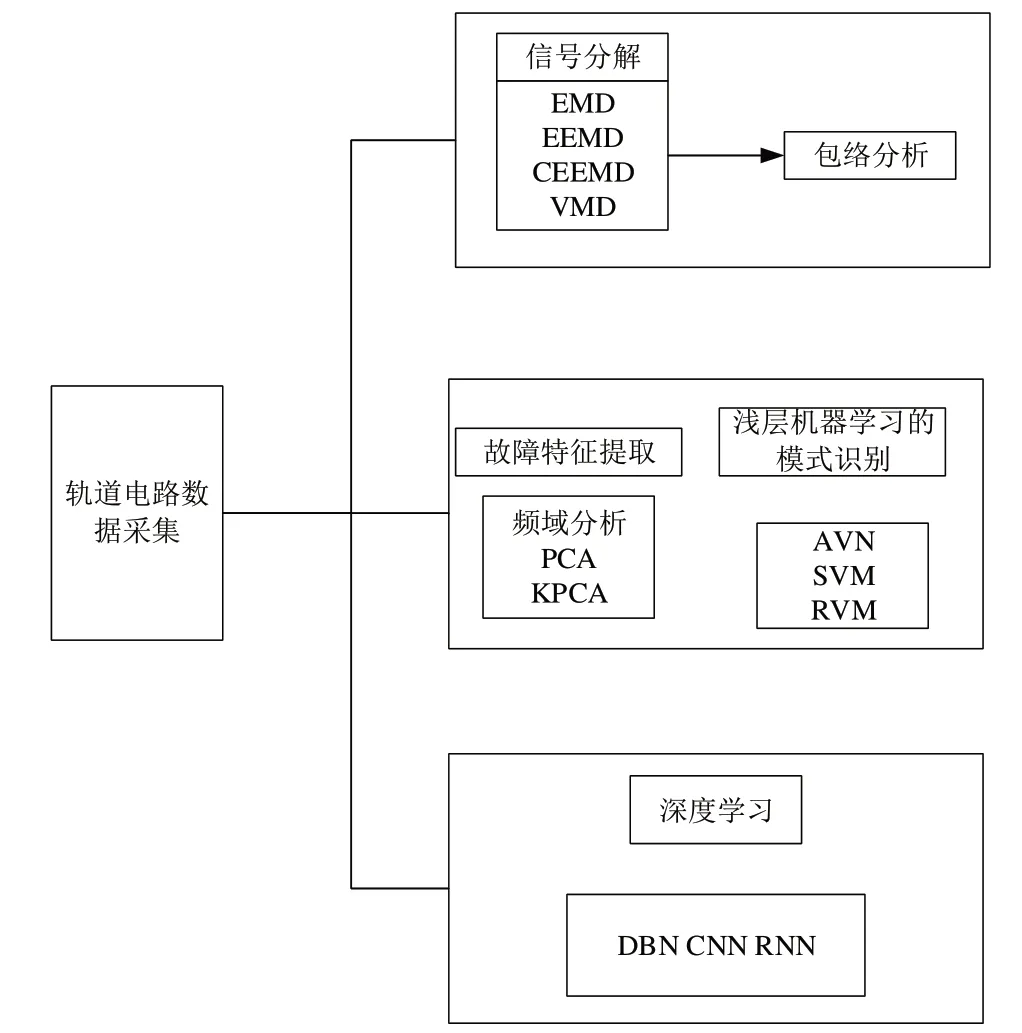
Fig.1 Technical route for fault diagnosis of uninsulated track circuits图1 无绝缘轨道电路故障诊断技术路线

主要分为3类：

第一种技术路线是对集中检测系统或轨道检测车传递的轨道电路信号进行处理与降噪，然后进行特征提取。再用上述方法对正常状态下的轨道电路进行特征提取，最后通过对以上两种特征信息的对比，得到轨道电路的故障信息，进而找到故障点［6］。此种路线大多在轨道电路轨面设备的在线分析中应用较为广泛，可在合适的条件下快速得出检测结果，在工程上应用的适用度高，一直是研究热点。但其局限性在于相比于处理单个故障点，该方法处理多个故障点的能力不是太强，且故障检测大多适用于轨面设备，如补偿电容等。

第二种技术路线将浅层机器学习方法与故障特征提取相结合，进而实现故障分类并诊断［7］。此种方法与第一种纯信号处理的方法有一部分重合，同样是先通过信号处理领域的方法实现降噪、分解、重构，最后进行故障特征提取。但与第一种方法不同的是，其将提取的特征输入到浅层机器学习方法中实现故障分类，得到故障类型。该方法不再局限于轨面设备，可实现更多类型的故障诊断，但不足之处是该方法比较依赖故障类型库中故障数据集的大小，在故障类型较少的情况下效果显著，在故障类型较多的情况下准确率会降低，且其依然依靠第一种技术路线中的故障提取方法［8］。

第三种路线则采用深度学习方法。深度学习是相对于浅层机器学习而言的，其具有比后者更深层的结构，还有较强的非线性特征提取能力，可以直接实现轨道电路信号中的故障特征提取，相比于信号处理方法中特征提取的复杂步骤，深度学习方法更加便捷、高效。相比于浅层机器学习，其可以应对更复杂的故障情况，且保持较高准确率。缺点是深度学习需要大量样本进行训练，但由于目前“状态修”代替“故障修”工作的开展，人工的日常维护使得轨道电路故障情况较少出现，导致故障数据集较少，该情况是深度学习方法的主要局限［9］。

此外还有研究将不同方法相融合对上述路线进行改进，以提高准确率。下面将对各类方法的具体应用进行说明。

2 基于信号分解的故障诊断方法

轨道电路上的故障大部分来自补偿电容的故障，随着环境的变化会出现容值下降或断线故障等情况，但是由于补偿电容数量太多以及铁路线路太长等原因，不能每一个故障都进行人工确认，。除补偿电容断线故障外，补偿电容容值下降及接触不良等故障只能由轨道检测车上的线圈间接感应到。针对这一问题，信号处理方法在铁路轨道电路故障诊断中得到了广泛应用，其可对频谱随时间的变化特性进行有效分析，对于处理感应电压与感应电流等较为复杂的信号效果显著。

2.1 经验模态分解

经验模态分解（Empirical Mode Decomposition，EMD）是1998 年由美国科学家Norden 博士提出的一种新型自适应信号时频处理方法，该方法依据数据自身的时间尺度特征进行信号分解，无须预先设定任何基函数［10］。

基于EMD 的时频分析方法既适合于线性、平稳信号分析，也适合于非线性、非平稳信号分析，这一点对于轨道电路非线性、非平稳的信息处理比较适用。有一个假设贯穿整个信号处理领域：任何复杂的信号均可视为多个不同的固有模态函数（Intrinsic Mode Function，IMF）叠加的结果，这些固有模态函数相互独立，且分为线性与非线性两种情况［11］。根据此假设，设需要分解的信号为x(t)，其EMD 分解步骤如下：

（1）生成原始信号的上下包络线，方法是以给定插值结点处的二阶导数值作为未知数求解构造三次样条函数。在整个信号中，连接极大值点形成上包络线，极小值点形成下包络线。

（2）计算每一点中的上下包络线均值，得到m1(t)：

（3）用原始信号x(t)减去包络线均值m1(t)，得到中间信号。

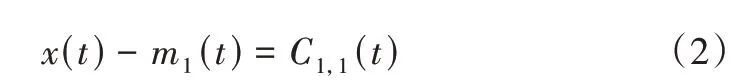
这就是原始信号x(t)筛分后得到新信号的过程C1，1(t)。

（4）由步骤（3）得到的新信号C1，1(t)，判断其是否满足上述IMF 的条件，如果满足，该信号就是一个IMF 分量；如果不满足，则将C1，1(t)看作新的原始信号，重新进行步骤（1）-（4）。直到分解k次后满足IMF 条件为止。

I1(t)代表原始信号x(t)中最高频的IMF 分量，IMF 分量的获取通常需要若干次迭代。

（5）从原始信号x(t)中减去I1(t)得到剩余分量r1(t)，随后将r1(t)看作新的原始信号，重复步骤（1）-（4）得到第二个IMF 分量I2(t)，再用r1(t)减去I2(t)后获得剩余分量r2(t)。如此分解下去，直到无法继续分解为止，从而完成对信号x(t)的EMD 过程。

（6）剩余的rn(t)为残余分量，为单调函数，所有IMF分量与残余分量之和为原始信号x(t)：

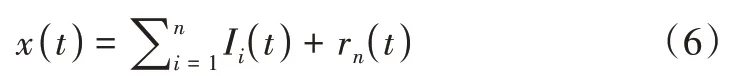
原始信号x(t)分解后的第一个IMF 包含原始信号的最高频率，同时也包含最低时间尺度。随着筛分过程的迭代，IMF 阶数增加，对应IMF 包含原始信号的频率成分降低，时间尺度升高，EMD 分解的收敛条件就是最后的rn(t)为单调函数，且此时rn(t)包含的原始信号频率最低，时间尺度不小于原始信号的时间尺度，因此可将rn(t)作为趋势项。

但其不足之处在于容易出现模态混叠与端点效应。模态混叠是指EMD 分解有不完全的情况，即多个不同频率分量共存于一个IMF 中，会影响后续信号分析。同理，最后的剩余分量可能混在最低一阶的IMF 分量里，使得剩余分量作为趋势项的提取不完全，影响后面的趋势判断。端点效应是指原始信号x(t)终究是有限的，在其两端的信号点用三次样条法生成上下包络线时，无法判断在两端是否存在极值点以及极值点的性质，所以三次样条法在此处插值时，不可避免地会出现信号失真的情况。以上两种情况都会使信号处理结果受到影响，进而导致故障诊断结果的准确率下降［12］。

2.2 总体经验模式分解与补充的总体平均经验模态分解

针对上述EMD 分解的不足，人们提出一种噪声辅助数据分析方法，即总体经验模式分解（Ensemble Empirical Mode Decomposition，EEMD）。在EMD 中如果极值点分布不均，会出现模态混叠问题，因此文献［13］将白噪声加入待分解信号，利用白噪声频谱的均匀分布，当信号加在遍布整个时频空间且分布一致的白噪声背景上时，不同时间尺度的信号会自动分布到合适的参考尺度上，并且由于零均值噪声的特性，经过多次平均后，噪声将相互抵消，集成均值的结果即可作为最终结果。

但EEMD 也引入了新问题，固有模态函数由于通过求取平均来近似而产生了相应偏差，且其在信号重构过程中残留了大量冗余噪声。为此文献［14］提出互补集合经验模态分解（Complementary Ensemble Empirical Mode Decomposition Method，CEEMD）方法，CEEMD 方法主要向原始信号中添加两个相反的白噪声信号，并分别进行EEMD 分解。CEEMD 不仅解决了EMD 引起的模态混叠问题，而且在保证分解效果与EEMD 相当的情况下，减小了由白噪声引起的重构误差。CEEMD 包括以下几个步骤：

（1）向信号中加入一对幅值相同、相位角相差180°的高斯白噪声，形成两个新信号，即：

（2）对信号x1和x2分别进行EMD 分解，将每组分解结果的总体平均记为IMF1和IMF2。

（3）求IMF1和IMF2对应分量的平均值，把该值作为CEEMD 的分解结果，即：

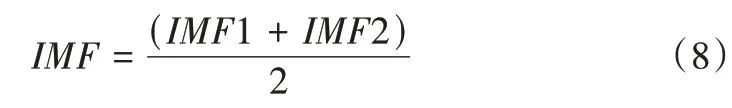
该方法不但克服了EMD 中的模态混叠和能量泄露现象，而且减少了EEMD 方法在信号重构过程中的白噪声残留，为轨道电路中的故障诊断提供了新方法。

2.3 小波包分解

小波分解可用于突变信号和有孤立奇异点函数的处理，通过小波分解能够在时域和频域内表征原始信号的局部特征。但是，小波分解对高频部分的分辨率低。小波包分解在小波分解的基础上，对信号的高频部分作进一步分解，克服了小波分辨率低的缺点，提供了更全面的信号分析。小波包变换建立在小波变换的基础上，其定义为：

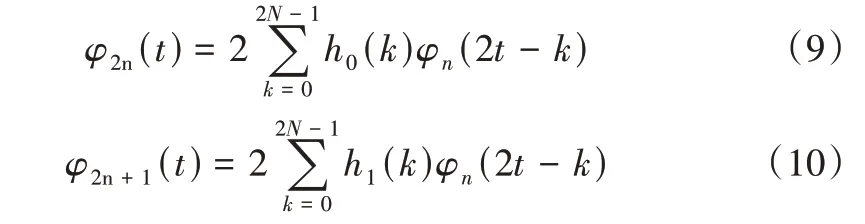
式中的h0(k)、h1(k)相当于长度为2N 的低通和高通滤波器。利用滤波器组实现小波包变换（Wavelet Package Transformation，WPT）的过程类似于小波变换（Wavelet Transform，WT），小波变换是通过一组基函数不停地分解低频，而对分解出的高频部分不作任何处理，但是小波包变换除分解低频外，也分解高频，得到的频带更加精确。

利用小波包可实现非线性信号分析，小波包分析将原始信号分解为多个时频带，此时可通过观察特定频带内的时变信号特征对原始信号进行分析。同时，小波包能量中包含大量故障信息，通过对特定频带计算其小波包能量并分析，可得到故障特征。文献［15］证明了小波包分析法在轨道电路故障诊断中取得了较好效果。

2.4 VMD变分模态分解

变分模态分解（Variational Mode Decomposition，VMD）是Konstantin 等［16］在2014 年提出的完全非递归模型，其可以同时提取模态分量。VMD 通过给定的原始信号寻找给定数目k 的一组模态，并确定其各自的中心频率，使其能够共同再现原始信号，同时满足每个模态解调到基带后都是平滑的。其本质是能够自适应地在各个波段运用经典的维纳滤波器。

相比于上述小波包分析法，当遇到轨道电路电信号中不存在突变信号和有孤立奇异点信号时，可以考虑VMD方法，其对采样噪声的鲁棒性更强。因为其变分模型优化的方式是采用交替方向乘子法，所以也避免了传统经验模态分解方法因循环递归分解导致的端点效应和模态混叠问题［17］。VMD 算法流程如下：

（1）采用Hilbert 变换，计算给定函数uk（t），获取其单侧频谱：

（2）将uk（t）与其对应的中心频率指数混叠，使其频谱转移到相应基带中。

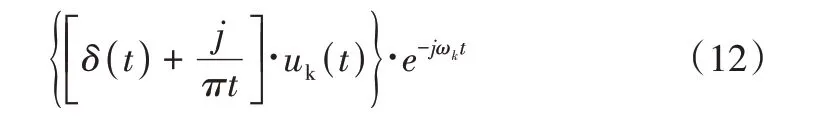
（3）根据高斯平滑度和梯度平方范数估计信号带宽。

（4）得到约束变分问题为：

式中，uk=｛u1，u2，...，uk｝为模态函数，ωk=｛ω1，ω2，...，ωk｝为各个模态函数对应的中心频率。为了将约束变分问题转变成非约束变分问题，引入拉格朗日算子λ（t）实现精确重构，以及二次惩罚因子α实现重构信号保真。两者结合后，得到拓展的拉格朗日表达式为：

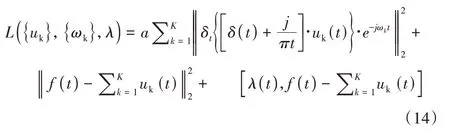
使用乘法算子交替方向法求解变分问题，迭代优化uk+1、ωk+1、λk+1，求解式（14），其最优解对应的模态分量为：

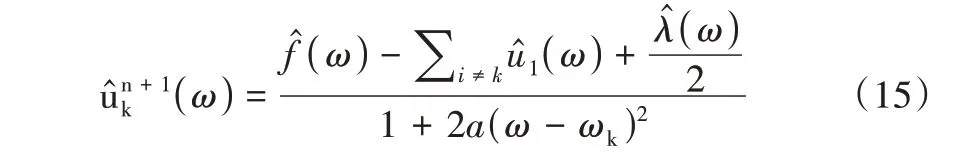
VMD 方法虽然可根据实际情况确定所给序列的模态分解个数，且在求解过程中可以自适应地匹配每种IMF 的带宽与最佳中心频率，还可以很好地实现IMF 的有效分离与其信号频域的有效划分，但其模态分量个数即k值与惩罚因子α的选取需要视情况而定，带有一定的主观性。换句话说，k与α的选取影响着VMD 分解效果。现在学术上普遍利用鲸鱼算法、灰狼优化算法等确定自适应函数，进而对VMD 算法进行改进。改进后的VMD 算法在轨道电路的补偿电容故障检测上取得了较好效果［18］。

以上几种信号分解方法并不是对轨道电路采集到的原始信号进行处理，而是需要建立相应模型，在模型中抽象出数据量，从而对得到的数据量进行信号分解得到特征值。信号分解方法应用于轨道电路故障诊断中的步骤一般是首先建立ZPW-2000A 轨道电路模型，然后利用模型抽象出可利用以上信号分解方法处理的数据，将其处理后提取故障特征，最后再通过特征分析、故障模式识别等方法达到故障检测的目的。

要建立轨道电路模型，首先要分析其原理。ZPW-2000A 轨道电路设备根据功能可分为发送端设备、轨面设备与接收端设备。当轨道电路无车占用时，发送端发送移频信号，移频信号沿着钢轨传输至接收端，接收端得到信号后控制驱动吸起轨道继电器或向车站给出轨道空闲的表示，这种状态又称为调整态；当轨道电路有车占用时，发送端发送移频信号，移频信号在流经列车轮对时，由于轮对的阻抗远远小于轨面上补偿电容的阻抗，移频信号则会通过轮对返回发送端，此时只有一小部分到达接收端。移频信号的数量远小于接收端驱动继电器吸起的阈值，所以继电器此时落下表示有车占用，此时移频信号列车的轮对分路也被称为分路状态。

在ZPW-2000A 轨道电路故障诊断中，由其工作原理可知，根据信号分解所需的原始信号不同，要选取不同的轨道电路状态，有时甚至要对分路状态与调整状态进行对比分析。通过分析轨道电路结构，在其发送端与接收端之间的设备其实都可以用一个等效四端网络来表示，整体模型即可表示为一个发送器与一个接收器之间级联一系列的等效四端网络，其中最常用的就是分路态模型，如图2所示。

Fig.2 Circuit breaker state model for uninsulated track circuits图2 无绝缘轨道电路分路状态模型

ZF为从分路点看去的等效阻抗，RF为列车分路轮对的等效电阻，W（x）为主轨道的等效四端网络模型，WXX为调谐区的等效四端网络模型，Wp、Wc分别为匹配变压器与传输电缆等效四端网络模型。模型得到的数据最终大多表现为轨道电路分路状态下幅值包络电流曲线或其归一化处理后的曲线，首先得到从分路点到发送端的等效四端网络矩阵F：

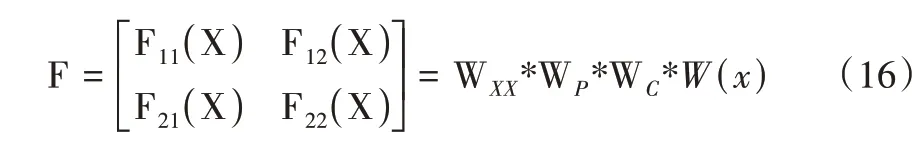
根据四端网络理论，网络端口的电压电流满足以下关系：

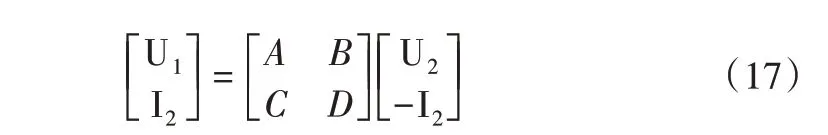
因此分路电流为：

最后通过信号分解方法对分路幅值电流信号进行分解处理，提取出故障特征。在轨道电路故障诊断领域常用的故障特征是经过信号分解后的各个频带的信号能量。利用信号能量得到各个分量的信号能量特征向量集，通过特征向量集判断故障点，实现轨道电路故障诊断。

3 基于浅层机器学习的故障诊断方法

以上信号分解方法主要针对ZPW-2000A 的室外轨道设备，大多用于补偿电容的故障诊断，而基于浅层机器学习的诊断方法通过采集到的更多数据集，可以检测更多故障设备以及判断出更多故障类型。

对于故障诊断，其理论基础本质上是数据挖掘，其中特征工程是数据挖掘的一项重要内容。对于轨道电路而言，故障特征的提取尤为重要，提取特征后即进行模式识别，从而实现故障诊断的目的［19］。

基于浅层机器学习的轨道电路诊断方法就是通过输入的特征信息进行模式识别，而获得特征信息所需的特征提取步骤则由于浅层机器学习的局限性，需要配合其他方法来完成，进而实现故障诊断。常见的轨道电路故障模类别如表1所示。

Table 1 Common track circuit fault categories表1 常见的轨道电路故障类别

3.1 轨道电路故障诊断中故障特征提取与选择方法

当对检测到的轨道电路信息数据进行观测时，这些数据常常拥有较为庞大的数据量以及较为复杂的变量关系，为大样本数据。大样本的数据集固然提供了丰富的信息，但是在一定程度上增加了问题的复杂性。

如果分别对每个指标进行分析，往往得到的结论是孤立的，并不能完全利用数据蕴含的信息。但是盲目地减少分析指标，又会损失很多有用信息。所以需要找到一种合适的方法，一方面可减少分析指标，另一方面可尽量减少原信息的损失。

由于不同指标中存在着相关关系，因此可考虑将关系紧密的变量合成一些新变量，使得新变量不相关，从而可以用较少变量来代表存在于各个变量中的数据信息。

以上叙述的就是降维的基本思想，降维有两种方法，一种是特征选择，另一种是特征提取。特征选择是直接消除不重要的特征，选择重要的信息留下，方法较为简单，存在一定的不准确性，可能丢失这些特征中的很多信息，常见的方法有频域分析法［20］。

特征提取则是通过组合现有特征来创建新变量，可以尽量保存特征中存在的信息［21］。但通常选取算法会较为繁琐，影响运行时间与诊断效率。常见的轨道电路故障检测领域的特征提取方法有主成分分析法（Principal Component Analysis，PCA）、核主成分分析法（Kernel Principal Component Analysis，KPCA）以及自适应层次聚类分析法等。下面对特征选择与特征提取的几种方法分别进行介绍：

（1）频域分析法。由于ZPW-2000A 轨道电路为无绝缘高频轨道电路，显然利用时域分析法不合适。频域分析是指直接处理通过轨道检测车获得的原始频率信号，主要针对载频信息与补偿电容两种数据。在轨道电路领域主要利用频率谱进行分析，而忽略频率统计特征。因为对频域信号的平均频率、均方根频率、中心频率和根方差频率等统计量进行特征选择，无法取得良好效果。在频谱分析方面，通过奇异谱、幅值谱、功率谱、倒频谱、细化谱等频域方法进行信号分析，可将得到的特征输入人工智能模型进行故障诊断。

（2）主成分分析法。其是一种多变量统计方法，可将一组存在相关性的数据转换为线性不相关的数据。其转换的核心就是正交变换，转换后的变量被称为主成分［22］，可以使用特征分解或奇异值分解（Singular Value Decomposition，SVD）的方法进行主成分分析。PCA 方法本质上是：现假设有一个n 维的数据集，PCA 通过改变该n 维数据集的基向量，对基向量的坐标轴与坐标原点进行平移，力求使变换后的数据方差最大，即让数据之间的相关性降到最低。变换后去掉正交轴，得到降维后的数据集。

轨道电路故障检测中常用奇异值分解进行PCA 降维，假设共有x个样本，每行是y维的，可看作x×y维的数据样本X，则根据SVD 方法，该数据集矩阵可分解为：

这里正交阵U的维数是x×y，正交阵V的维数是y×y，Σ是y×y 的对角阵。接下来将Σ分割成r列，记作Σr，利用U和V便能得到降维数据点Yr：

PCA 方法可用来删除单个特征，也可以减少多个特征。以下有一些策略来帮助判断到底该减少多少特征：

（1）根据对轨道电路的原理分析选择一个合适的特征数目，该方法高度依赖于数据集本身的特征以及后续的分析模型，且有一定的主观性。

（2）通过计算每个成分因子，能够解释原始数据变异的百分比，然后将不同成分因子所能解释的变异百分比相加，即得到了一个值，被称为累积变异百分比。在PCA 过程中，将选择能使该值最接近于1的维度个数。

（3）根据上一步骤得到的百分比，进而判断减去多少特征。

KPCA 本质上是一种新的非线性PCA 方法，该方法的基本思想是：对样本进行非线性变换，在变换空间进行主成分分析以实现在原空间的非线性主成分分析［23］。其算法步骤如下：

通过核函数计算矩阵K={Kij}n×n，其元素为Kij=k(xi，xj)。其中xi和xj为原空间的样本，k(·，·)是核函数。

计算K的特征值，并从大到小进行排列，找出由特征值对应的特征向量al，并对al进行归一化（||al||=1）。原始样本在第l个非主成分下的坐标为：

其中，xi是指第i个样本al的维度与样本数相同。如果选择m个非线性主成分，即计算K的前m个特征值及相应特征向量，则样本x在前m个非线性主成分上的坐标构成了样本在新空间中的表示。

聚类是通过无监督的方式将数据对象以类或簇为单位进行划分，将具有较高相似度的数据划分为同一个类，不同类之间的相似度差别较大。

层次聚类算法属于无监督的分类算法，聚类结果要求类别之间具有良好的可分性，即：类间距离尽量大，类内距离尽量小。由于聚类之前需要人为指定聚类个数或设定相应门限，文献［24］提出一种自适应层次聚类算法，使其能够根据自定义判别函数的取值来自适应确定聚类个数，以适用于轨道电路的特征提取。对于具有n个特征的输入样本x，综合考虑类内类间距离对样本的可分性，定义类内类间距离判据J（x）为：

最后取轨道电路某一点至其前方发送端所有分路点位置处的感应电压幅值数据的标准差作为特征，构成k×（m+1）维的特征矩阵Φ，表示为：

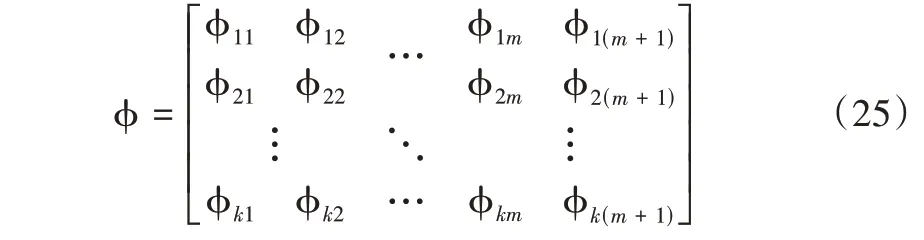
其中，Φ（i=1，2…k）表示轨道电路中所有感应电压包络幅值数据的标准差，反映了所有电容状态对感应电压幅值波动的影响；随后对特征矩阵Φ进行重构，对重构后的矩阵进行自适应层次聚类，以达到故障特征提取的目的。

3.2 浅层机器学习的故障诊断方法

目前在故障诊断领域，浅层机器学习方法可分为监督学习与非监督学习两大类，也有介于两者之间的半监督学习的特殊情况。常用的监督类学习方法主要有人工神经网络（Artificial Neural Network，ANN）、支持向量机（Support Vector Machine，SVM）、相关向量机（Relevance Vector Machine，RVM）等模式识别方法，这些方法各有优缺点，通常与不同的信号处理方法和其他特征提取方法及其对应的优化算法相融合，以实现轨道电路故障诊断，而无法独自实现特征自提取与识别。

聚类分析法主要应用于非监督学习，聚类与分类相对应，聚类方法不需要样本的训练标签即可对数据根据其特征属性进行聚合分类，常用的聚类方法有最近邻分类器等。但聚类方法在数据集较大、维度较高的情况下应用较为困难。文献［25］建立了基于最小二乘支持向量机的轨道电路故障诊断模型，网络结构如图3所示。

在轨道电路的故障诊断中选取输入最小二乘支持向量机模型中的特征量时，要满足特征量之间的独立性要尽可能大，输入量对输出量的影响也要尽可能大，且容易被设备检测出来。基于浅层机器学习进行故障诊断通常用主轨道输入电压、小轨道输入电压、衰耗盘电压等数据作为故障诊断特征量。

Fig.3 Fault diagnosis model of track circuit based on least squares support vector machine图3 基于最小二乘支持向量机的轨道电路故障诊断模型

在基于机器学习轨道电路故障诊断训练过程中，比较关键的一步就是对数据进行预先的归一化处理，防止不同单位与数量级带来训练中的混乱及不准确性。常用的归一化方法如下：

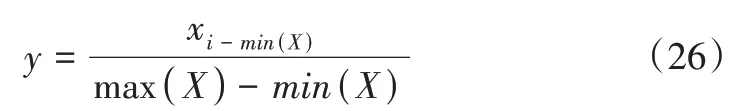
其中，xi为原始数据，min（x）、max（x）分别为原始数据中的最小值与最大值，y 为归一化数据。处理后的数据被输入到最小二乘向量机模型中进行训练，针对轨道电路的多种故障，采用一对一的方法对k类轨道电路进行故障诊断，对每个类别的样本和其他类别样本之间一对一地构建二值分类器，每个二值分类器只用相关的二类训练样本进行训练，一共可构造出k（k-1）/2 个二值分类器。在对测试样本进行识别时采用“投票法”，将测试样本输入给k类中第m类样本和第n类样本构造的二值分类器。如果输出结果判定测试样本属于第m类，则给第m类加一票；如果输出结果判定测试样本属于第n类，则给第n类加一票。当所有的k（k-1）/2 个二值分类器对测试样本分类后，k类中的哪一类得票最多，则判定测试样本属于这一类。

选取合适的核函数宽度与调节常数值，得到决策函数，完成该模型的训练，即得到轨道电路故障诊断的最小二乘向量机模型。

文献［26］将粒子群算法（Particle Swarm Optimization，PSO）用于支持向量机的参数优化，提出基于粒子群支持向量机的故障诊断模型，并将其运用于轨道电路中，结果优于随机的参数选取。粒子群算法的主要思想是在可解空间中初始化一群粒子，每个粒子由位置、速度和适用度值确定，适用度值由适用度函数计算得到。粒子在解空间中运动，通过跟踪个体极值点和群体极值点来更新自己的位置。个体极值是指个体所经历位置中计算得到的适应度最优位置，群体极值是指种群中所有粒子搜索到的适应度最优位置。粒子不断地更新位置，每更新一次即重新计算一次适应度值，再通过比较适应度值，更新个体极值和群体极值。

在每一次迭代过程中，粒子通过个体极值与全局极值更新自身的速度和位置，更新公式为：

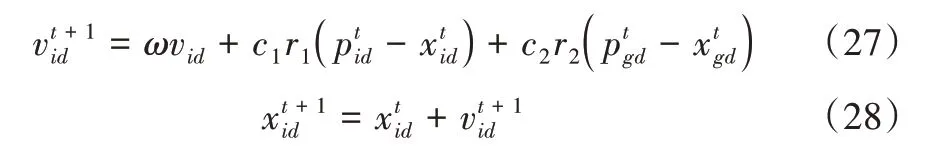
式中，ω为惯性权重；t为当前迭代次数；vid为粒子速度；c1、c2为非负常数，称为加速度因子；r1、r2为分布于［0，1］之间的随机数。

以径向基函数（Radial Basis Function，RBF）为核函数的支持向量机中有2 个参数：惩罚参数c和核函数参数g。其中，惩罚参数c用于控制超出误差的样本惩罚程度，核函数参数g表示径向基函数RBF 的宽度，c、g对于SVM 的分类准确率有着很大影响。因此，将两个参数（c，g）构成一个微粒，采用粒子群优化算法寻求较优参数，提高了SVM算法故障诊断的准确率和效率。

以上两种基于SVM 算法的情况，前者的准确率及参数选取的稳定性不如后者，后者则会面临陷入局部最优解的问题。为解决粒子群算法陷入局部最优解的问题，文献［27］提出将模拟退火算法（Simulated Annealing，SA）与粒子群最小二乘支持向量机结合的方法。

SA 算法的思想源于物理中固体物质的退火过程，整个过程与一般的组合优化问题类似，SA 算法能以一定的概率接受恶化解。此概率由其新解与原解对应目标函数的绝对差值、温度参数T共同决定，T减小则概率减小。概率计算如下：

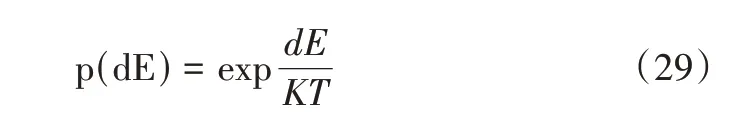
虽然传统的SA 算法具有非常好的全局搜索能力、概率突变能力，但仍有一些不足：

（1）在T较大时，迅速收敛至全局最优解，易错失当前最优解。

（2）过度依赖参数。若T0较大，衰减步长太小，会导致收敛速度过慢，反之，若T0较小则易丢失全局最优解。针对以上不足，利用遗传（GA）算法的变异思想，在SA 算法中引入简单变异算子：即引入一个变异概率P，随机对当前更新后粒子中的一个变量再次初始化。如果P 小于随机数，则进行自适应变异操作，否则放弃，从而在变异过程中增大种群搜索空间，针对性地改善PSO 算法寻优能力的不足，保证其跳出局部最优解，得到全局最优解，以提高收敛速度和寻优精度。

4 基于深度学习的轨道电路故障诊断方法

随着我国铁路事业的飞速发展以及轨道检测车检测系统和集中检测系统的高度自动化，针对轨道电路的状态检测将产生大量数据，这些数据不仅维度较高且数据量庞大。对于浅层机器学习而言，有两个方面无法很好地处理。数据集太大会导致其计算时间变长，且浅层机器学习面对高维数据无法很好地实现降维，需要结合其他方法。与浅层机器学习相对的就是深度学习，以深度学习为主的方法恰好弥补了浅层机器学习的缺点，因此在轨道电路故障诊断领域逐步得到应用。

目前，在轨道故障诊断领域应用广泛的主要有卷积神经网络（Convolutional Neural Networks，CNN）、深度置信网络（Deep Belief Network，DBN）、循环神经网络（Recurrent Neural Network，RNN）等深度学习方法。文献［28］利用深度置信网络与海洋捕食者算法优化后的最小二乘支持向量机（Least Squares Support Vector Machine，LSSVM）提取故障特征，并取得了较好效果。

深度置信网络DBN 是一种由多层隐藏受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）堆叠而成的概率生成模型，其典型结构如图4所示。

Fig.4 Multilayer hidden restricted boltzmann machine probabilistic generative model图4 多层隐藏受限玻尔兹曼机概率生成模型

RBM 由可见层v和隐藏层h构成，每一层的单元之间都有双向连接，但每一层中的单元互相独立。可见层神经元可表示为v=｛v1，v2，…，vn｝，隐藏层神经元可表示为h=｛h1，h2，…，hm｝，其能量函数为：

其中，wij为可见层单元i与隐藏层单元j的连接权值，ai为可见层单元i的偏移量，bj为隐藏层单元j的偏移量。

DBN 方法对于轨道电路故障特征的提取过程分为预训练和微调两个阶段。在预训练阶段，将不同类型的轨道电路故障数据输入到深度置信网络的第一层RBM 进行无监督训练，将训练得到的输出作为下一层的输入，以此逐层传递贪婪学习，直到输出层输出轨道电路故障特征。微调阶段是一个有监督学习的过程，将输出结果与标签数据进行对比，利用误差反向传播算法对DBN 进行逆向训练，完成参数寻优，进而提取出故障特征。然后采用海洋捕食者（Marine Predators Algorithm，MPA）智能算法对LSSVM 的惩罚因子和核函数参数进行寻优，并建立最优MPA-LSSVM 诊断模型。最后，将DBN 提取的特征样本导入诊断模型进行轨道电路的故障分类识别。

文献［29］利用卷积神经网络创建轨道电路故障诊断模型，将轨道电路诊断主机的实时变化数据作为神经网络的输入，将实际使用中常见的故障类型作为输出，建立输入与输出之间的映射关系。在选取深度学习样本数量的问题上，如果采取单个样本的方法更新参数，会陷入局部最优，影响神经网络的性能和泛化能力，因此在处理深度学习样本数的问题上选用了批处理方法。但使用该方法没有完全消除上述问题，批处理数目较少会严重影响迭代速度，同时极易陷入局部最优；而批处理数目较多会导致无法找到最优参数，批处理数目选择过于繁琐。

文献［30］针对轨道电路调谐区故障，通过CNN 中的卷积层实现轨道电路调谐区特征提取，并对比不同卷积层参数下的诊断准确率及训练时间，选择当前条件下相对最优的卷积层参数。同时针对训练中可能出现的过拟合现象而采用dropout 函数，并通过CNN 中第二全连接层实现故障分类。此外，还考虑到人为构建数据集时数据标签错误的问题，通过构建标签错误数据集的方式，减小错误标签数据对训练过程的影响，取得了比较全面、良好的效果。

文献［31］运用深度信念网络的无监督学习对故障数据进行训练，得到最优参数值并提取出故障数据高层的分布式特征。选择BPNN 作为分类器，以无监督学习输出的参数作为BPNN 初始值，完成反向调优，实现了轨道电路的15 种故障分类。利用数据进行多次验证，证明了其准确性与有效性。文献［32］提出一种具有长短期记忆的循环神经网络，通过对网络进行训练实现故障诊断。

以上介绍的基于深度学习的故障诊断方法，相比于传统的浅层机器学习，其在故障诊断流程方面有着创新性的发展。传统的浅层机器学习首先进行数据预处理，然后进行特征提取，最后选择分类器；深度学习方法则是在数据预处理之后直接设计模型，然后直接训练得出结果。深度学习的特征提取并不依赖于人工，而是由算法自动完成，虽然降低了一些可解释性，但其在很大程度上解决了如何提取特征以及提取特征的有效性问题。

深度学习方法的学习能力非常强，尤其是在特征工程、故障诊断等应用中表现非常好，只要有足够的数据驱动，可以将故障诊断的准确率保持在较高水平。此外，其适应范围也比传统的机器学习广泛，里面的神经网络层数很多、宽度很广，可以映射到轨道电路的很多函数中，实现综合故障诊断。

铁路行业自动化与智能化程度的加快，势必要在日常生产中产生大量数据。在轨道电路故障诊断中，适合浅层机器学习的特定简单任务会越来越少，而对于基于深度学习的方法，数据量越大，深度学习的表现越好，非常适用于未来的铁路故障诊断。

深度学习在轨道电路故障诊断中的大致发展方向是需要更便捷的设备和更加契合的算法模型。现在深度学习所需的硬件设备尚不足以移植到移动端，无法满足铁路高效运营与维护的要求，因此未来需要运算能力更强、更加小巧快捷的移动端来支撑深度学习故障诊断模型，以提高运营效率。如今在轨道电路方面利用深度学习方法进行故障诊断通常采用现成的模型，虽然也取得了不错的准确率，但是没有针对轨道电路乃至整个铁路系统的故障诊断算法，故障诊断效果还有很大的提升空间。综上所述，基于深度学习的方法必定会成为今后铁路行业故障诊断领域应用的主要方法。

5 结语

本文总结了现阶段以轨道检测车采集与集中监测系统得到信号为数据集的轨道电路故障诊断方法的3 类技术路线，详细介绍了3 类技术路线中常用的具体方法，并且在前人基础上对这些方法发展现状和本身的局限性进行了梳理。基于信号处理的方法虽然应用的轨道电路故障类型较为单一，大多数只有轨面设备，但由于准确率与实时性较高，应用较为广泛，依旧是研究热点；基于浅层机器学习的方法针对较少数据集有着很好的准确率与运算效率，但其特征提取等关键步骤的过程有些繁琐，常需要与其他方法结合；深度学习有着以上两者的优点，但对数据集大小的要求较高。然而在大数据时代下，这种要求也较容易满足，因此基于深度学习的轨道电路故障诊断方法将成为今后轨道电路故障诊断的主要思路。