基于DWT的相似性搜索算法

谭章禄,袁 慧,王福浩

(1.中国矿业大学(北京) 管理学院,北京 100083;2.华北电力大学 控制与计算机工程学院,北京 102206)

一、引 言

时间序列数据(TSD)是大数据中广泛存在的数据类型之一。时间序列数据挖掘(TSDM)的最终目标是从原始或转换的时间序列数据中发现隐藏的信息,其中聚类和分类任务最为普遍。时间序列聚类和分类任务广泛存在于金融、医学、气象等领域,比如在金融领域中基于股价的相似性,构建有效的股票市场分类体系,有助于预测同一集群中其他公司的股价[1],优化投资组合策略[2],为投资者决策提供可靠参考;在公共卫生领域中基于聚类方法分析新冠肺炎疫情时间序列特征[3];基于Sentinel-2遥感时间序列植被物候特征分类方法精准获取滨海湿地植被时空分布信息[4]。在大数据生态系统中,为了满足实际应用的多元化需求,研究TSDM对政府和企业建设智能系统、释放数据要素潜力、提高智能决策能力、更好赋能经济发展具有重要意义。

TSDM任务最主要的技术基础是时间序列降维和相似性度量。时间序列降维的目的是减少计算时间和所需的存储空间,因时间序列减少而丢失的信息量并不妨碍获得正确的结果[5]。Aghabozorgi等对各种降维方法进行了研究[6]。比较经典的技术有傅里叶变换(DFT)[7]、离散小波变换(DWT)方法[8]。小波变换是具有多分辨率特性的时间—频率分析方法,特别适合非平稳、非线性时间序列数据的处理。张海勤等基于DWT方法对序列数据进行分解后采用尺度序列来近似表示原始序列,以达到大幅度简约数据量的效果[9]。此外,一些学者提出基于时间序列特征的降维方法,如基于关键形态特征[10]、基于独立成分分析(ICA)等降维方法[11],但在降维的过程中如何更恰当地保留有用信息仍是重要的研究问题。

目前已有很多相似性度量方法。1993年Agrawal等将时间序列相似性问题定义为在大规模的时间序列数据库里,通过一定的相似性匹配方式,查询出和已知序列相匹配的时间序列集合,并且率先使用欧氏距离(ED)度量时间序列间的相似度[7]。时间序列数据的相似性度量通常以近似的方式进行,根据度量函数不同主要分为基于距离和基于特征两类。一方面,基于特征的相似性度量方法包括但不限于基于关键点的相似度量、基于模式异同匹配的相似度量等[12-13]。另一方面,基于距离的相似性度量方法最早采用的是ED,但ED方法往往对异常值和噪声比较敏感,且不能从整体上度量时间序列的趋势变化。随着研究的深入,动态时间弯曲(DTW)和最长公共子序列(LCSS)被认为是TSDM中应用最广泛、最有效的方法[14]。DTW本质上是通过时间轴的拉伸和收缩来度量时间序列之间的相似性,解决了ED无法度量时间长度不一致的时间序列的问题[15],但DTW的时间复杂度更高。LCSS本质上是通过定义和确定相似性阈值来衡量时间序列的相似性[16],但LCSS对相似度阈值的大小比较敏感。为了弥补经典方法的不足,很多最新的改进方法被提出,比如分段时间扭曲距离(STW)、基于LCSS的单变量离散有限时间序列相似性度量方法(DLCSS)等[17-18],但是上述方法均不能说明一个特定的方法适用于任何时间序列数据库。因此,选择合适的相似性度量方法是影响TSDM结果质量的另一个重要因素,是影响聚类、分类以及模式识别等挖掘任务的关键,以准确和快速的方式支持时间序列相似性度量是近年来TSDM研究中一直考虑的问题之一[19]。整体来说,现有方法主要存在以下方面的局限:

(1)全局性低。现有方法通常只关注时间序列中对应时间点的关系。

(2)敏感性强。度量结果受不同时间序列间的数值大小影响,特别地,对异常值和噪声比较敏感。另一方面,强烈依赖于参数的取值,例如LCSS方法需要用户指定相似度阈值的合适取值。

(3)效率低。高维时间序列数据通常对存储的要求较高,同时复杂的计算过程也会导致挖掘过程呈指数级地变慢。

针对时间序列聚类方面,根据聚类是基于原始数据还是基于特征可分为两类。基于原始数据的聚类方法是指在聚类过程中不处理原始数据,而是通过拉伸和收缩非线性轴直接匹配两个时间序列。例如基于DTW的时间序列模糊聚类方法[20]、基于标准化的互相关度量定义时间序列之间的距离以实现聚类[21]。而基于特征的方法本质上是将原始时间序列数据转化为低维的特征向量,然后使用聚类方法对特征向量进行处理。Moller-Levet等提出基于形状来度量短时间序列的相似性[22],形状是由振幅的相对变化和时间信息形成,并采用模糊c均值(FCM)算法实现时间序列聚类。因此,本文通过基于特征的时间序列聚类方法验证所提算法的有效性。

综上所述,时间序列降维方法和相似性度量方法的选择会影响TSDM结果的准确性和效率,然而已有方法在处理带有噪声、随机性强和非线性的时间序列数据时存在一定的局限性。为了更好地处理TSDM各种任务,本文研究面向时间序列数据挖掘的时序降维和相似性度量问题,并验证所提的方法是否可以进一步提升时间序列聚类的效果。

本文的主要贡献在以下几个方面:第一,提出一种基于局部高频离散小波变换的时间序列降维消噪方法,同时提出一种基于波动特征的相似性度量方法,分别从波动的相对偏差和一致性定义时间序列间的相似程度;第二,提出一种基于局部高频离散小波变换的时间序列相似性搜索算法,同时解决了时间序列降维和相似性度量问题,提升了结果质量和搜索效率;第三,提出一种基于相似性搜索的时间序列k-medoids聚类方法,并应用于解决时序聚类问题,结果表明其在聚类准确率、确定聚类数目和聚类中心等方面均表现得更好,对处理时间序列聚类任务具有重要的现实意义。

二、相关研究

本部分首先介绍DWT的基本思想,然后提出基于波动特征的时间序列相似性度量方法,揭示该方法的性质和优点,对应前两点局限。由于可以通过移动窗口技术将非等长序列匹配转换为等长全序列匹配,因此这里仅讨论等长序列匹配。假设Xt=(x1,x2,…,xn)为长度n的时间序列数据。

(一)DWT的基本思想

DWT是小波变换的离散形式。小波变换是首先把母小波(mother wavelet)函数进行位移,然后在不同尺度条件下与Xt作内积。由于小波变换计算复杂度高,且存在信息表述的冗余性,因此变换需要进行离散化。设φ(t)为一个母小波,DWT的公式表示如下:

(1)

尺度函数表示为:

φj,k(t)=2-j/2φ(2-jt-k),j,k∈Z

(2)

小波函数表示为:

φj,k(t)=2-j/2φ(2-jt-k),j,k∈Z

(3)

DWT针对尺度参数a和平移参数b按2的幂级数进行离散化处理,并对时间进行均匀离散化取值,常用的是二进制小波变换。离散化的尺度时间一般要求为2,4,6,…,2n。在不同的尺度和时间下,分别构造尺度函数向量空间V与小波函数向量空间W并进行卷积,分别得到近似信息和细节信息。离散小波变换的阈值处理过程如图1所示[23]。

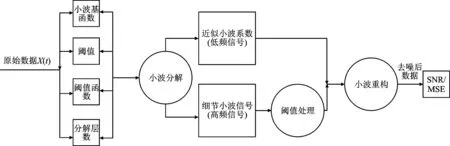
图1 离散小波变换阈值法去噪过程

首先,Xt在给定的小波基函数和分解层数等参数下实现不同频率的信号分解,分别获得低频和高频两类信号。其中,低频信号集中了数据的大部分信息并作为下一步的输入变量,直至得到确定分解层数对应的低频信息,而高频信号反映了细节上的差异;然后,通过阈值原则与阈值函数过滤掉高频信号中的噪声,将剩下满足条件的细节小波系数子集作为特征并构成特征空间;最后,将低频信号和不同尺度下处理后的高频信号重构以获取降噪后的时间序列。

(二)基于波动特征的相似性度量

一条时间序列的波动特征定义为该序列形态变化的波动程度和波动方向。两条时间序列的波动特征是否相似是由波动程度的相对偏差和波动方向的一致性度量,其中相对偏差包含原始序列和波动幅度序列两部分。由此,本文将在ED的基础上融合波动幅度和秩相关系数的概念,提出一种新的相似性匹配方式来计算时间序列间的非相似性,命名为形态波动一致性偏移距离(MFCDD)。任意两条长度为n的时间序列Xt和Yt(t=1,2,…,n)的MFCDD为:

(4)

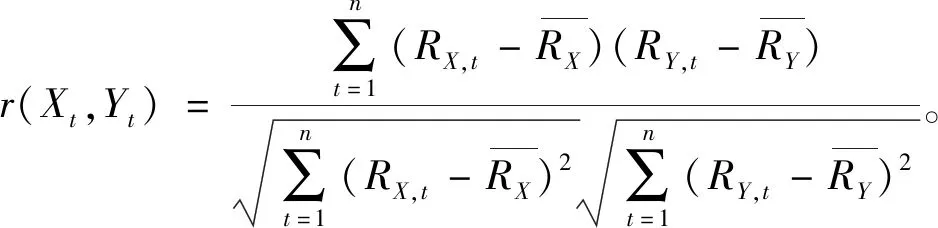
MFCDD方法使用的逻辑如下所述:

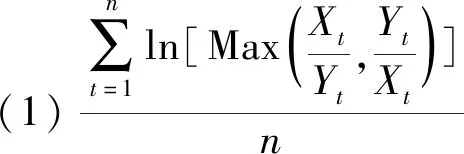
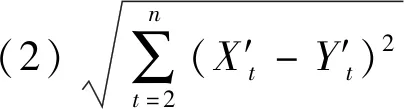
(5)

(3)r(Xt,Yt)代表时间序列Xt和Yt的波动趋势的一致性,取值范围为[-1,1]。通过计算秩相关系数表示两时间序列从波动方向和程度上的趋势一致性。

(4)最后将相对平均偏差与波幅的相对偏差相加,减去波动方向上的一致性,得到时间序列Xt和Yt在形态上的非相似程度,然后执行反对数计算。

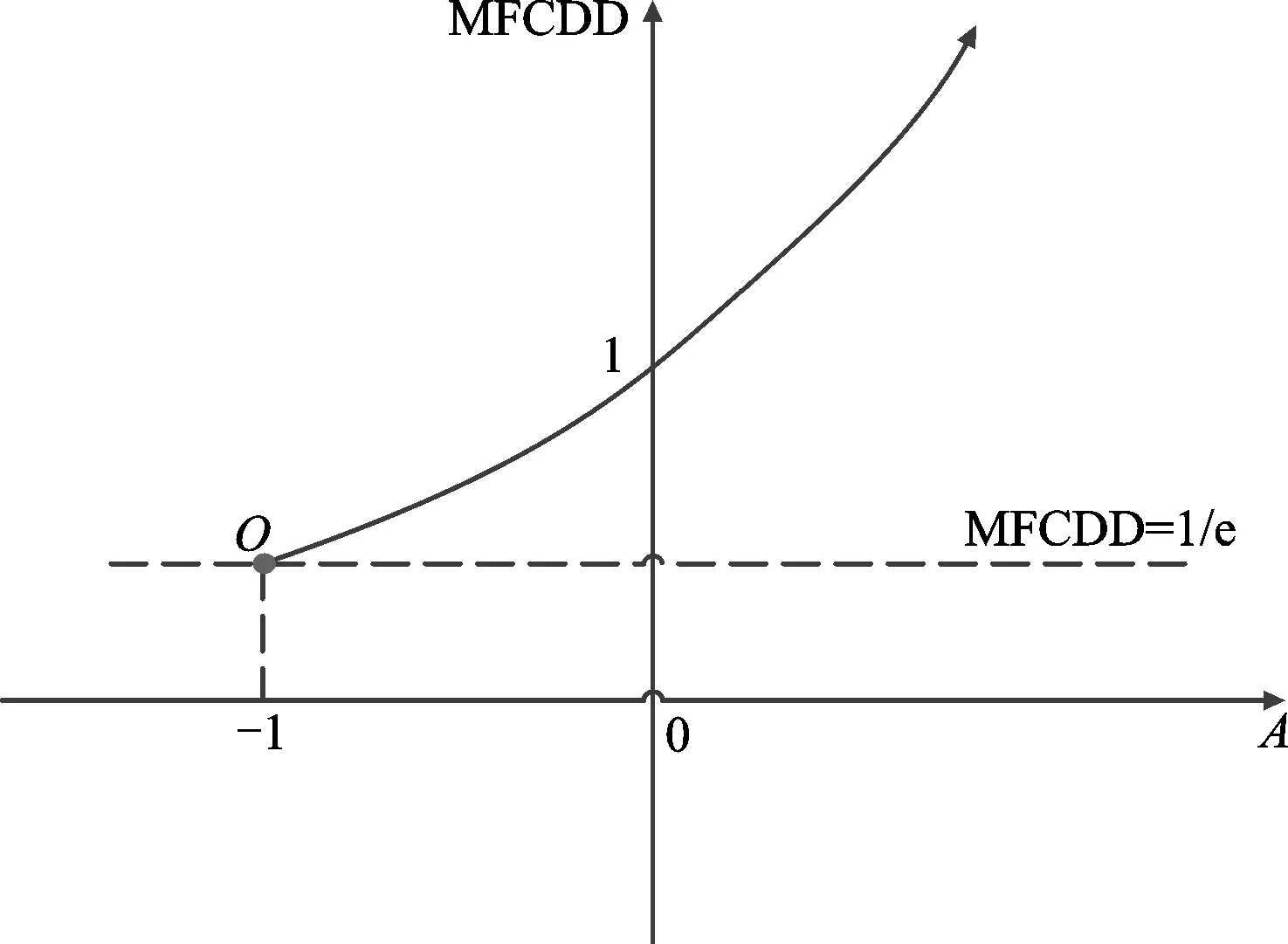
图2 相似性度量方法MFCDD的曲线图

该方法共分为两部分:一部分是相对偏差,一部分是一致性。当原始序列和波动幅度序列之间的相对偏差和越小,趋势一致性越高,那么MFCDD的取值就会越小,说明两序列的相似性程度越高。这两部分是相互制衡的关系。该方法结合了波动幅度、ED和秩相关系数的概念,产生了简洁而周全的时间序列相似性度量方法。与其他距离度量方法不同的是,它不仅对原始时间序列进行了相对偏差的计算,还对变换后的波动幅度时间序列中对应的衍生数据点进行了相对偏差的计算,其代表了一个新的特征序列,两者融合可以全面地获取序列中变化趋势的信息,减少异常值、序列取值大小带来的影响。图2展示了MFCDD方法的曲线图。

由图2可知,MFCDD是一条指数型曲线,取值范围为[1/e,+∞),对应A的取值范围为[-1,+∞)。当两条时间序列完全相同时,A为-1,这时MFCDD取最小值,为1/e≈0.367 88。不难看出,相似性度量方法MFCDD(Xt,Yt)具有以下性质和优点:

(1)恒大于0。MFCDD(Xt,Yt)>0。MFCDD值越小,说明两时间序列间的相似性程度越大,反之,则相似性程度越小。

(2)对称性。MFCDD(Xt,Yt)=MFCDD(Yt,Xt)。

(3)无参数。该方法在进行时间序列挖掘任务时不需要指定输入参数,克服了LCSS方法的不足,不会因参数敏感性影响相似性度量的准确率。

(4)低敏感性与全局性。如果只计算相同时间点的对应关系则会增加对异常值的敏感性。该方法同时计算了两序列之间的秩相关系数和波动幅度序列点的对应关系,一方面可以从整体上观察时间序列的形态趋势变化,另一方面提高了对序列形态相似性的注意力,提高了序列形态相似性搜索的精确度。

(5)时间复杂度低。针对长度均为n的两时间序列,MFCDD的时间复杂度为O(n)+O(n-1)+O(1),即复杂度为O(n),小于时间复杂度为O(n×n)的DTW方法。

三、基于DWT的相似性搜索算法

该算法共分为两步:第一步是时间序列数据的DWT处理,阐述了所提的局部高频DWT降维消噪方法的基本原理,对应第三点局限;第二步是相似性搜索算法,给出了搜索算法的计算步骤。

步骤一:基于DWT的时间序列降维消噪

DWT方法具有逐步操作的特点。每个步骤的输入都是通过正交镜像滤波器(QMF)对传递,由于算法中加入了滤波器理论,分解后的小波系数的个数由floor((n-1)/2)+N计算得到。其中,floor表示向最小值取整数,n代表原始信号的长度,N为滤波器长度的一半,所以小波系数并不能精确地减半。因此,输出的高频信息和低频信息的长度均约为输入信号长度的一半,也就是每一步的输入长度将减少约2倍。

需要强调的是,在逐步分解的第一步中,输出的高频信息包含了原始信号的大部分噪声,小波系数经过阈值过滤后几乎变为零。因此,基于这种特性,在重构小波系数时不予考虑第一步输出的高频信息,也就是说经过阈值过滤后,仅重构最终分解层数的低频信息和除第一步以外的高频信息。这样重构后的数据不仅过滤了确定噪声,同时维数约缩为原始数据长度的50%。本文将该方法定义为局部高频离散小波变换(LHFDWT)。LHFDWT方法中参数取值的依据为:阈值函数采用软硬阈值的改良折衷法,具体公式参见郭晓霞和杨慧中的研究[24],其中阈值σ=mean(|wj,k|)/0.674 5,是在张维强和宋国乡采用方法基础上做了进一步改良[25];小波基函数采用Daubechies小波,是因为dbN可以更好地提取数据集的特征,具体取值为db6。该方法的主要优点为:

(1)计算简洁。该方法的主要思想是在DWT基础上省略第一步分解的高频信息;

(2)保留了较多信息。与其他降维方法相比,该方法没有提取特征向量,而是基于去噪的角度通过综合考虑尺度序列和小波序列,在实现降维的同时尽可能地保留整体趋势和局部特征。

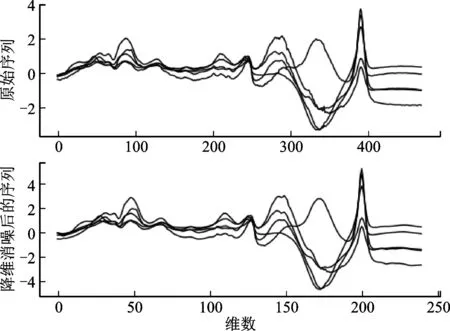
图3 原序列集和LHFDWT序列集

例如5维470列的Beef时间序列数据集实施分解层数为5层(db6)的LHFDWT处理,重构序列和原序列的对比效果如图3所示。从图3中可以看出,LHFDWT方法对原始序列进行了降维和噪声过滤,降维消噪后的序列准确地反映了原序列的主要趋势和局部特征,信号也变得更加清晰(长度由470降到240)。另外,对于不满足长度是2的整数倍的时间序列采用缩首处理,这里限于篇幅,不再详述。

步骤二:相似性搜索算法

在所提的LHFDWT和MFCDD方法的基础上,本部分给出时间序列相似性搜索算法的计算步骤。

针对m维n列的时间序列数据集X(m,n)和查询时间序列Qj(j=1,2,…,n),首先利用LHFDWT方法对X(m,n)和Qj进行降维消噪处理,然后规范化预处理;最后利用相似性度量方法MFCDD搜索X(m,n)中与Qj最相似的序列。具体的计算步骤在算法1中给出。

算法1 LHFDWT-MFCDD相似性搜索算法

1.输入时间序列数据集X(m,n)和查询时间序列Qj(j=1,2,…,n);

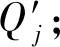
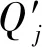
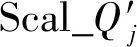
5.输出查询时间序列Qj的最相似序列X。

(6)

根据上述步骤可得算法的时间复杂度。针对长度均为n的两时间序列,降维消噪的时间复杂度为O(n),采用MFCDD方法度量长度为k的LHFDWT序列间相似性的时间复杂度为O(k),这里的维数k通常小于长度n,因此整个算法的时间复杂度近似为O(n)。

四、基于DWT的相似性搜索算法在时间序列聚类中的应用

时间序列相似性搜索通常转化为时间序列聚类问题。为了发现时间序列数据集的聚类结构和类别,本文采用k-medoids聚类和1-NN分类技术验证所提的搜索算法的效果,并与DTW和LCSS方法的性能进行比较。本部分首先给出基于所提的相似性搜索算法的时间序列k-medoids聚类方法的计算步骤,然后对UCR标准时间序列数据集进行聚类实验。实验在Intel(R)Xeon(R)Gold 6248R CPU x64 @3.00 GHz 2.99 GHz (2处理器)、64 GB内存和Microsoft Windows 10操作系统下进行,本研究所需的所有程序均用Python3.7软件编写,多进程参数为48。

(一)基于相似性搜索算法的k-medoids聚类

k-medoids聚类是基于划分的聚类方法之一。与其他的聚类方法相比,k-medoids聚类方法具有对属性类型没有局限性、鲁棒性强等优点[26],而且簇中心是真实的观测对象。首先,在观测数据中随机地确定K个对象作为初始簇中心,即用实际对象代表簇,一个代表对象代表一个簇。其次,根据剩下的每个对象与各个簇中心的MFCDD值,将剩下的每个对象分配到最相似的簇。对于每个簇,随机再选择一个非代表对象,并计算与剩下的对象的总MFCDD之和。最后,尝试所有可能的替换,观测一个非代表对象替换一个代表对象时所提高的聚类质量。当聚类质量不再提高时,迭代结束。因此,该方法的目标函数采用MFCDD,代表最小化每个对象到其簇中心的非相似度之和。

所提出的k-medoids聚类方法的计算步骤在算法2中给出。在算法2中,步骤1～3与步骤5就是所提的相似性搜索算法;总代价C是以s作为代表对象时计算的MFCDD之和与以xi作为代表对象时计算的MFCDD之和之间的差值。

算法2 LHFDWT-MFCDD-k-medoids算法

1.输入包含n个对象的数据集X={x1,x2,…,xi,…,xn},聚类数目K;

2.对X进行LHFDWT降维消噪和规范化预处理;

3.从X中随机选择K个对象xi作为初始的代表对象;

4.repeat;

5.采用MFCDD方法将每个剩余的对象分配到最相似的代表对象所代表的簇中;

6.随机地选择一个非代表对象s;

7.计算用s替换代表对象xi的总代价C;

8.ifC<0,thens替换xi,形成新的K个代表对象的集合;

9.until不发生变化,将n个对象聚成K个类:C1,C2,…,Ck;

10.输出K个类:{D1,D2,…,Dk},其中Dk={xi∈Ck}。

(二)数据选取

本研究采用的实验数据是来自开放的UCR标准时间序列数据集(https://www.cs.ucr.edu/eamonn/time_series_data_2018/)。数据集的名称和情况如表1所示。每个时间序列数据集都有已经划分好的两个子集,即训练数据集和实验数据集。在每个子集中均指定了每个时间序列的类,例如Ham数据集有两个类,训练和实验数据集中的时间序列数分别为109和105,每个时间序列的长度为431,需要先进行缩首处理,降维后的序列长度由430变为220。训练数据集用于识别最佳的聚类数目,以及在最佳聚类数目下的聚类准确率和聚类中心,实验数据集用于分类,计算分类准确率,验证聚类中心的代表性。

(三)性能评估标准

本文使用在最佳的聚类数目下聚类算法的运行时间(T/s)来衡量搜索效率,时间越短,表示搜索算法的效率越高,反之越低;使用准确率衡量时间序列相似性搜索的精度,包括聚类准确率和分类准确率。设时间序列数据集X(m,n)内的序列总数为M,其中类别识别正确的序列个数为P,则准确率的公式为:

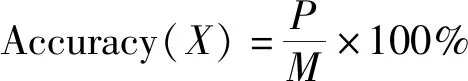
(7)

Accuracy(X)取值越接近于100%,说明属于类别识别正确的时间序列数越多,算法搜索匹配能力越好,准确率越高,反之越低。聚类准确率记为Acc_clu,分类准确率记为Acc_cla。

(四)k-medoids聚类实验框架

基于k-medoids聚类和1-NN分类技术识别训练数据集和实验数据集的类别,并分别与时间序列的真实类别进行比较,计算聚类准确率和分类准确率。具体步骤如下:

第一步:时间序列数据集预处理。首先采用LHFDWT方法分别对训练数据集和实验数据集进行降维消噪,然后进行规范化预处理。

第二步:评估最佳的聚类数目、聚类准确率和最佳的聚类中心。首先,利用基于三种相似性度量方法(DTW/LCSS/MFCDD)的k-medoids聚类方法分别对预处理后的训练数据集进行聚类,结合拐肘方法确定不同方法下的所有训练数据集的最佳聚类数目。然后,以最佳的聚类数目对训练数据集再一次进行聚类,得到对应的聚类准确率、最佳的聚类中心和搜索效率T。

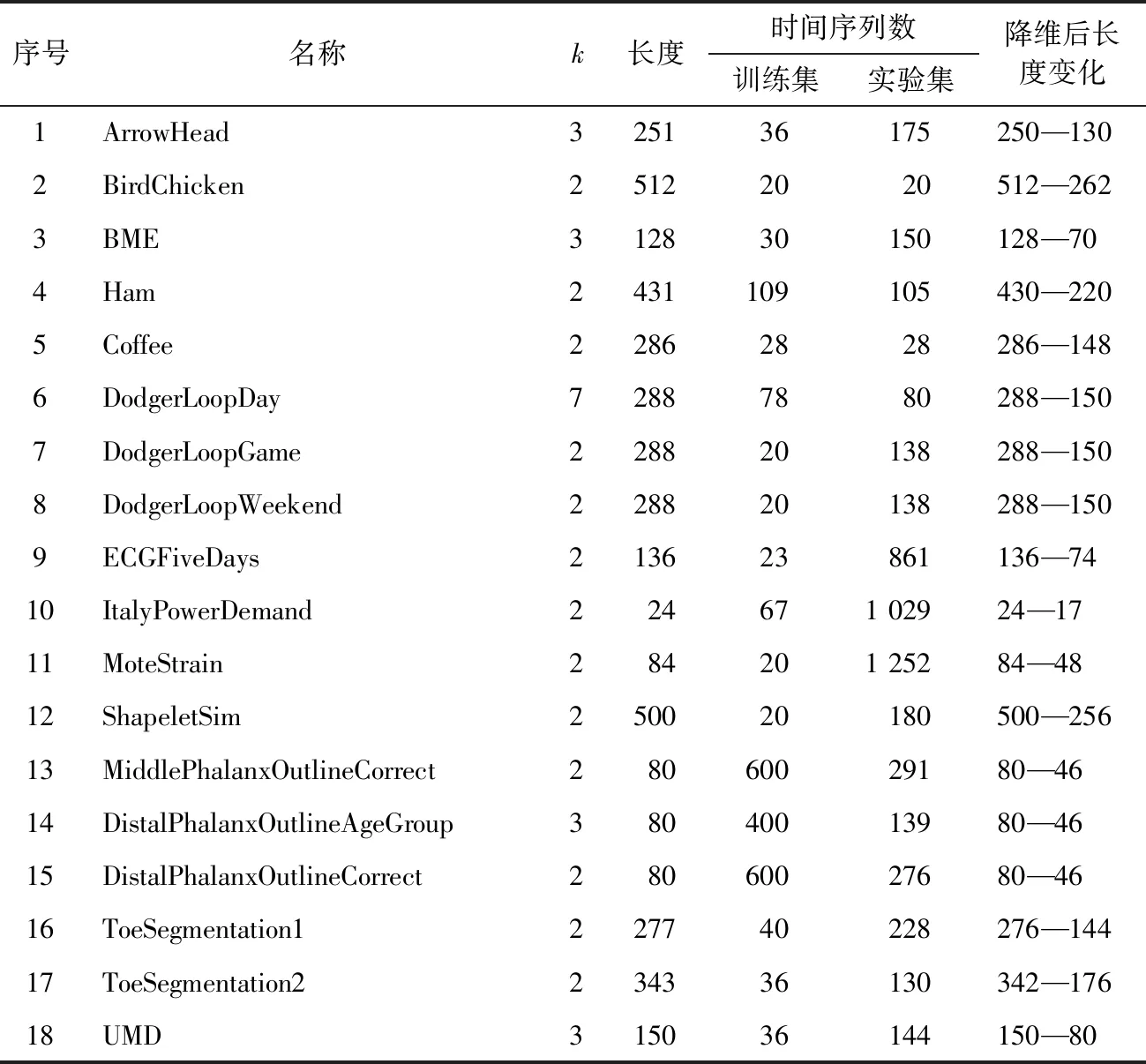
表1 数据集的名称和情况

其中,聚类准确率是训练数据集中分配到正确类别的时间序列个数与序列总数的比值。拐肘法旨在帮助找到数据集合适的聚类数,它是一个二维图,x轴表示聚类数目,y轴表示不同集群簇的序列与各自集群簇的聚类中心的总距离(总的非相似度)之和。根据该方法,集群簇的最佳数目是所有元素的总距离的变化量很小时对应的集群簇的数量。

第三步:识别实验数据集的类别,验证聚类中心的代表性。在DTW/LCSS/MFCDD三种方法下,根据第二步得到的聚类中心采用1-NN分类技术,依次与实验数据集的任意时间序列计算距离值或非相似度,其最小值对应的聚类中心就是该时间序列最相似的序列,将最相似的聚类中心代表的类别等效为该时间序列的类别。分组准确率是实验数据集中分配到正确类别的时间序列个数与序列总数的比值。

图4是k-medoids聚类实验框架图。其中,基于DTW的k-medoids聚类方法,记为A1;基于LCSS的k-medoids聚类方法,记为A2;基于MFCDD的k-medoids聚类方法,记为A3。

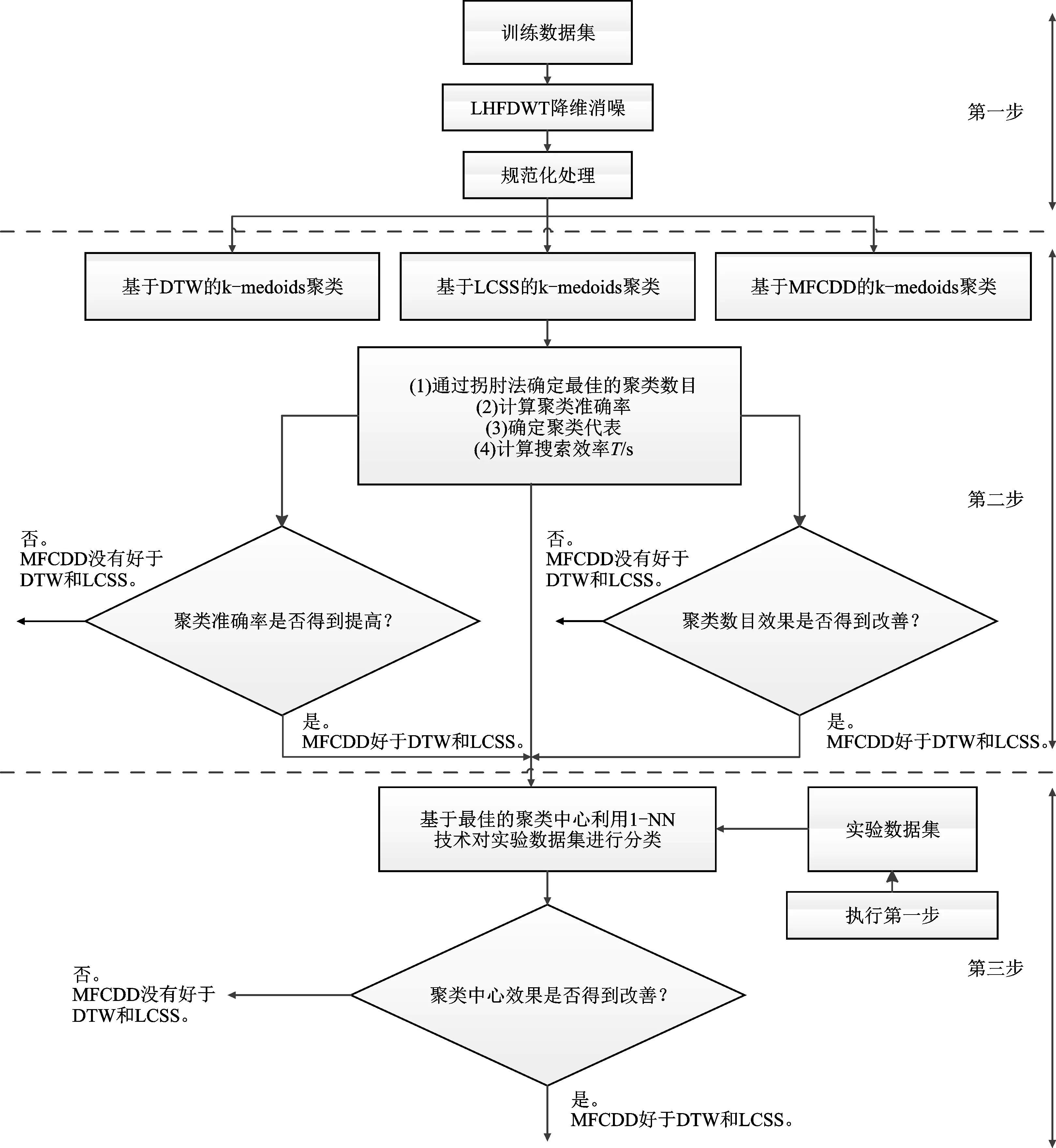
图4 k-medoids聚类实验框架图

表2代表了基于三种相似性度量方法(DTW/LCSS/MFCDD)的k-medoids聚类方法的相同点和不同点。目标函数的具体公式为:

(8)

(9)

表2 三种不同相似度的k-medoids聚类方法的具体特征

其中,K为集群簇,ki为集群i的元素(i=1,2,…,K),Si为集群i的聚类中心,MFCDD(x,Si)代表集群i中序列x与聚类中心Si的相似度。

基于相似性搜索的k-medoids聚类过程主要回答以下问题:

问题1:在MFCDD方法下的聚类准确率是否优于DTW和LCSS?

问题2:MFCDD方法在确定聚类数目方面的效果是否优于DTW和LCSS?

问题3:在搜索效率上所提的相似性搜索算法是否得到提升?

问题4:MFCDD方法在确定聚类中心方面的效果是否优于DTW和LCSS?

为了回答这些问题,分别在18个时间序列数据集上实施聚类。聚类过程的假设如下:

(1)对于每个集群簇数,聚类操作重复100次。

(2)在每次迭代中,随机聚类中心初始化试验次数最多可以更换100次。

(五)实验结果

1.聚类结果

表3说明了针对18个训练数据集基于DTW、LCSS和MFCDD方法的k-medoids聚类结果,包括最佳的聚类数目,在最佳聚类数下的聚类准确率、搜索效率。若聚类数目评估正确,则加粗。

在DTW结果中,例如对真实类别为2的Coffee数据集,所确定的最佳聚类数目为3,其中28.57%的时间序列被正确分配到所属的聚类集群中,所用时间为510.49 s。可以发现,所有训练数据集的平均聚类准确率为31.41%,平均运行时间为2 892.11 s,聚类数目的正确率为22.22%。有趣的是,ShapeletSim数据集和UMD数据集的聚类准确率为0。

在LCSS结果中,Coffee数据集所确定的最佳聚类数目为2,与真实类别数相同,其中67.86%的时间序列被正确分配到所属的聚类集群中,所用时间为287.56 s。可以发现,所有训练数据集的平均聚类准确率为 31.11%,平均运行时间为9 964.57 s,聚类数目的正确率为27.78%。另外,LCSS与DTW的平均聚类准确率无明显差异。

在MFCDD结果中,Coffee数据集所确定的最佳聚类数目为2,与真实类别数相同,其中78.57%的时间序列被正确分配到所属的聚类集群中,所用时间为67.18 s。可以发现,所有训练数据集的平均聚类准确率为51.07%,平均运行时间为1 209.94 s,聚类数目的正确率为66.67%。

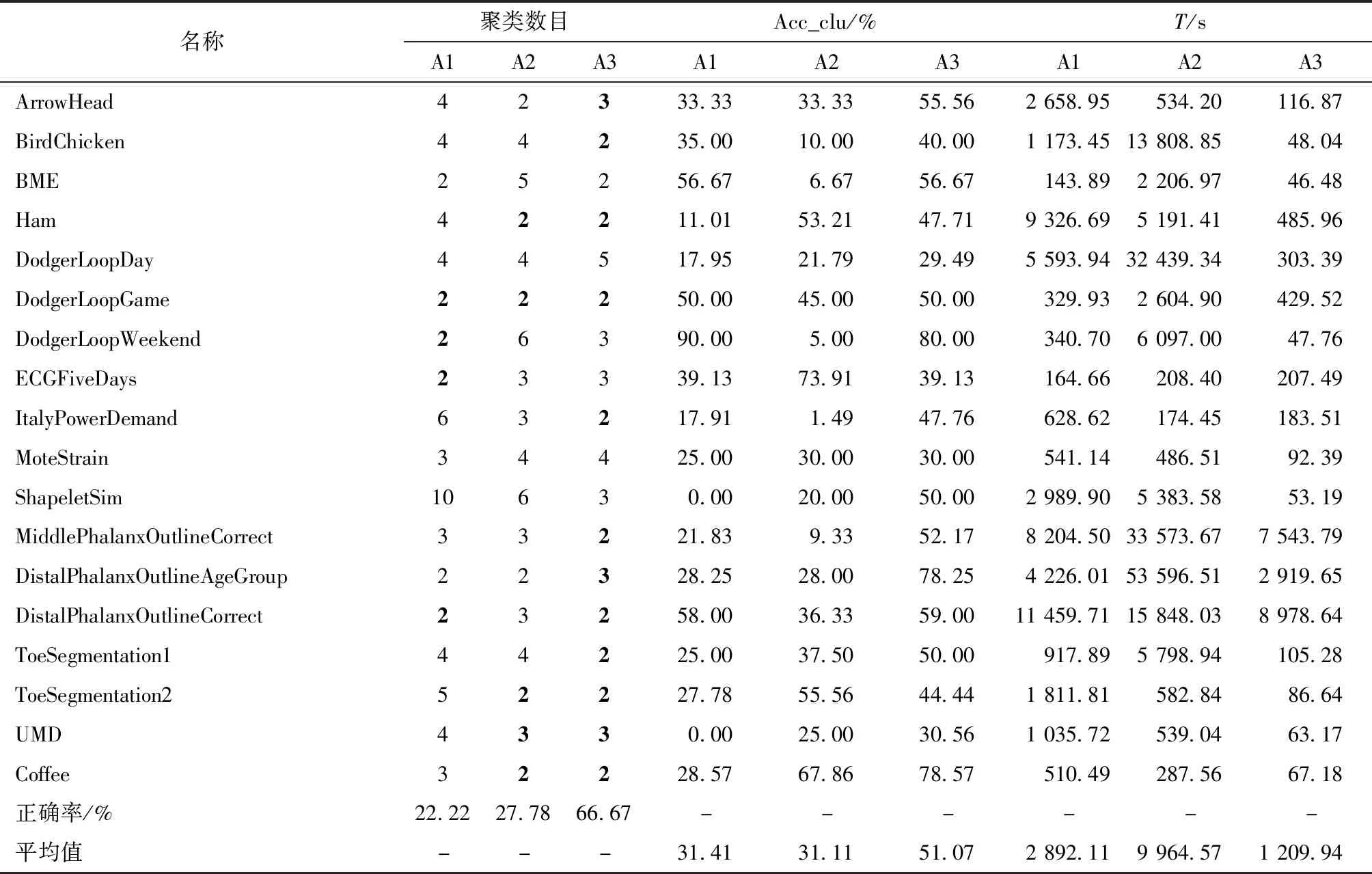
表3 基于DTW、LCSS和MFCDD的k-medoids聚类结果

表3的结果回答了问题1～3,可以看出MFCDD方法的聚类结果优于DTW和LCSS方法,聚类数目的正确率、聚类准确率更高,并且运行时间更短,说明在所提的相似性搜索算法下聚类精度和效率均得到提升,且具有稳定性。表4具体给出了A3与A1、A2方法在聚类准确率和运行时间上的结果对比。

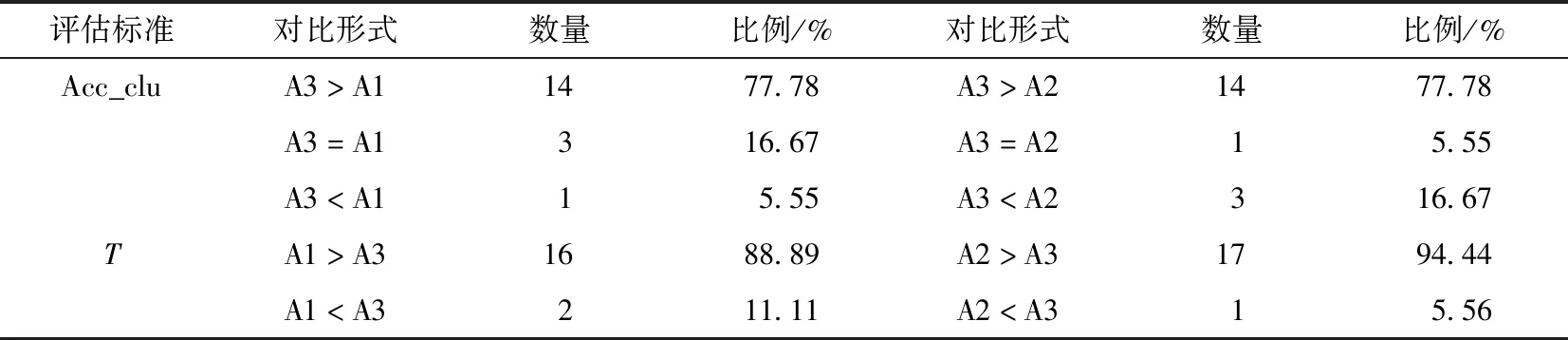
表4 聚类准确率、运行时间和SC分值的结果对比

表4结果表明,聚类准确率方面,在94.45%的情况下,MFCDD下的聚类准确率大于或等于DTW下的聚类准确率;在83.33%的情况下,MFCDD下的聚类准确率大于或等于LCSS下的聚类准确率。运行时间方面,在88.89%的情况下,MFCDD下的运行时间低于DTW下的运行时间;在94.44%的情况下,MFCDD下的运行时间低于LCSS下的运行时间。

表5具体给出了A1、A2和A3方法确定正确的聚类数目的结果对比,分别统计了与真实类别数相同、与真实类别数相差1、与真实类别数目相差多于1三种情况。可以发现,A1、A2和A3方法聚类数目评估正确的数量分别为4、5和12个数据集,而且A3方法聚类数目评估多于1个错误的数量仅有2个数据集,说明在确定正确的聚类数据方面,MFCDD方法的效果更好。

为了进一步说明结果的有效性和稳定性,本文使用配对样本t检验对Acc_clu进行验证。通过正态分布检验发现,两组配对A1-A3、A2-A3的差值均近似服从正态分布,满足配对样本t检验的条件。

表5 数据集聚类数目评估的正确数量

第一组假设:

H0:ud=A1-A3=0,代表A1和A3方法的Acc_clu无显著性差异。

H1:ud=A1-A3≠0,代表A1和A3方法的Acc_clu有显著性差异。

第二组假设:

H0:ud=A2-A3=0,代表A2和A3方法的Acc_clu无显著性差异。

H1:ud=A2-A3≠0,代表A2和A3方法的Acc_clu有显著性差异。

以上两组假设分别用于比较A1、A3方法和A2、A3方法,结果如表6所示,α=0.01,统计量t为:

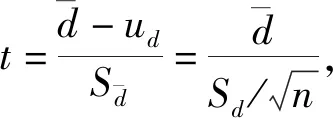
(10)

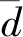
表6结果表明,k-medoids聚类在A1和A3、A2和A3方法下均拒绝原假设,相对于A1方法,A3方法显著提升了聚类准确率,t=-4.33,P=0.000 4,置信度为99%;相对于A2方法,A3方法显著提升了聚类准确率,t=-3.19,P=0.005,置信度为99%。因此,可以认为A3方法下的k-medoids聚类准确率优于A1和A2方法。

表6 三种方法的配对样本t检验结果

综上所述,与LCSS和DTW方法相比,k-medoids聚类技术在MFCDD方法下可以更好地识别数据集的聚类数目,具有更高的聚类准确率,聚类结果具有更好的效果和稳定性,相比DTW方法,平均聚类准确率提高了62.59%,同时搜索效率更高,相比LCSS方法,平均运行时间降低了87.86%。

2.分类结果

为了回答问题4,根据训练数据集在最佳的聚类数目下确定的聚类中心,基于三种不同的相似性搜索算法(DTW/LCSS/MFCDD),采用1-NN分类技术对实验数据集进行分类,实验结果如表7所示。例如Coffee实验数据集在DTW、LCSS和MFCDD方法下分别达到了28.57%、53.57%和85.71%的分类准确率。对于所有实验数据集在DTW、LCSS和MFCDD下的平均分类准确率分别为27.32%、40.23%和47.39%,说明基于MFCDD的相似性搜索算法匹配的时间序列相似度更高,表明确定的聚类中心更具有代表性。

为了进一步说明结果的有效性和稳定性,本文使用配对样本t检验对Acc_cla进行验证。通过正态分布检验发现,两组配对DTW-MFCDD、LCSS-MFCDD的差值均近似服从正态分布,满足配对样本t检验的条件。

第一组假设:

H0:ud=DTW-MFCDD=0,代表DTW和MFCDD方法的Acc_cla无显著性差异。

H1:ud=DTW-MFCDD≠0,代表DTW和MFCDD方法的Acc_cla有显著性差异。

第二组假设:

H0:ud=LCSS-MFCDD=0,代表LCSS和MFCDD方法的Acc_cla无显著性差异。

H1:ud=LCSS-MFCDD≠0,代表LCSS和MFCDD方法的Acc_cla有显著性差异。

以上两组假设分别用于比较MFCDD、DTW方法和MFCDD、LCSS方法,α分别为0.01、0.15,统计量t这里不再重复,结果如表8所示。

表8结果表明,聚类中心的分类结果在两组检验下均拒绝原假设,相对于DTW方法,MFCDD方法显著提升了分类准确率,t=-4.50,P=0.000 3,置信度为99%;相对于LCSS方法,MFCDD方法显著提升了分类准确率,t=-1.56,P=0.138,置信度为85%。因此,可以认为MFCDD方法下聚类中心的分类准确率优于DTW和LCSS方法。

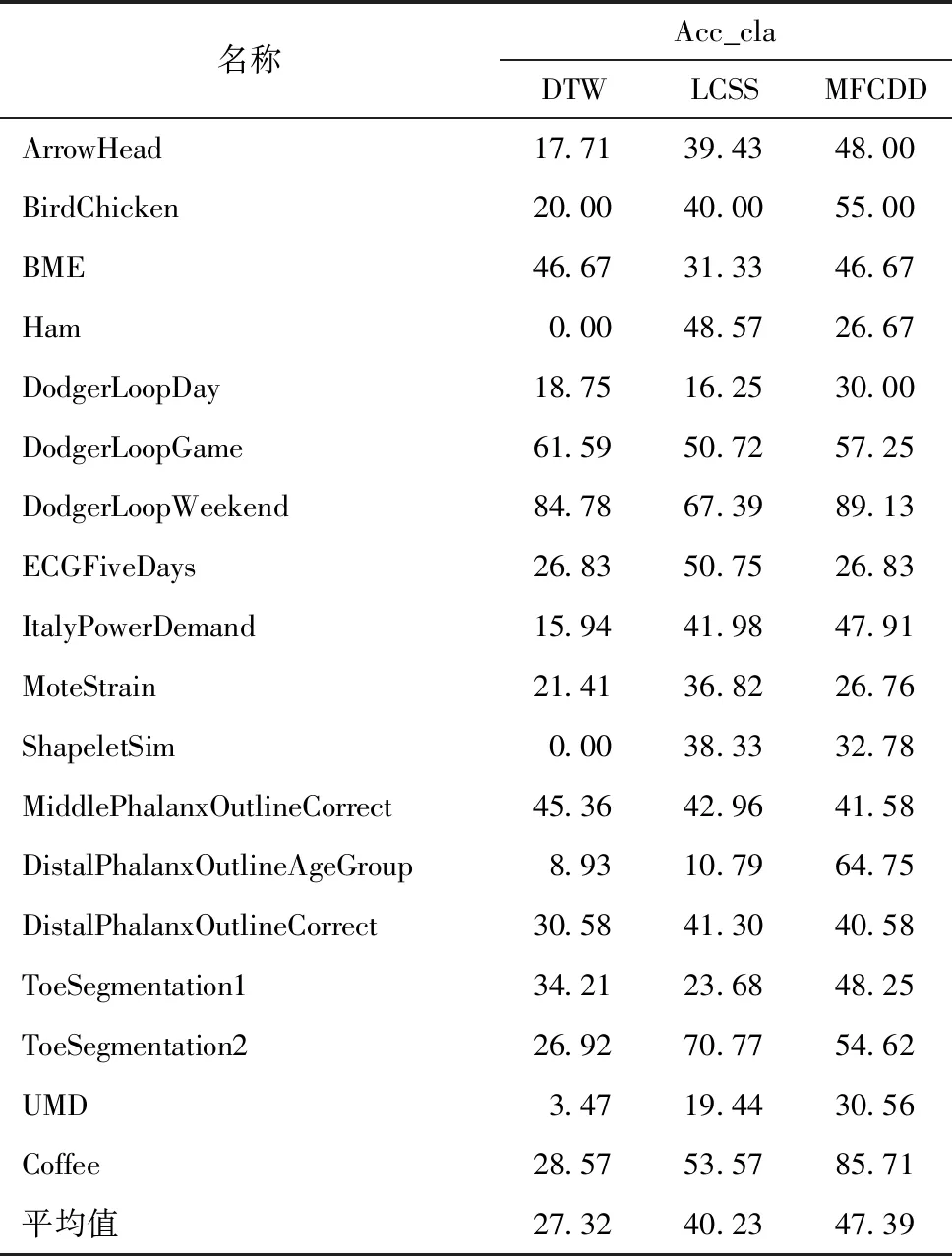
表7 不同相似性搜索算法的1-NN分类的实验结果

表8 三种方法的配对样本t检验结果

表9具体给出了DTW、LCSS和MFCDD方法在分类准确率上的结果对比。结果表明,在88.89%的情况下,MFCDD下的分组准确率大于或等于DTW下的分组准确率;在61.11%的情况下,MFCDD下的分组准确率大于或等于LCSS下的分组准确率。

表9 分类准确率的结果对比

综上所述,与LCSS和DTW方法相比,k-medoids聚类技术在MFCDD方法下可以更好地识别数据集的聚类中心,代表性更好,相比DTW方法,平均分类准确率提高了73.46%。

五、结 论

在大数据和人工智能背景下,针对时间序列数据挖掘中时序降维和相似性度量两个核心问题,本文提出了一种新的相似性搜索算法,应用于时间序列聚类任务,旨在提高聚类准确率和效率。该算法主要分为预处理和相似性度量两方面。预处理包括降维消噪和规范化处理。针对降维消噪预处理,本文提出局部高频离散小波变换(LHFDWT)方法,该方法同时考虑了近似信号和局部细节信号,对时间序列进行降维的同时也实现了噪声过滤,且保留了原序列的主要趋势和局部特征,提高了后续挖掘任务的效率。针对相似性度量,本文基于波动特征提出时间序列相似性度量方法,称为形态波动一致性偏移距离(MFCDD),波动特征是由序列波动的相对偏差和方向一致性形成。该方法在一定程度上弥补了现有方法存在的全局性低、敏感性强和效率低等局限。同时应用于时间序列聚类任务,提出一种基于相似性搜索的时间序列聚类方法。

基于18个UCR时间序列数据集的实验结果表明,基于DTW、LCSS和MFCDD的k-medoids聚类技术,训练数据集的平均聚类准确率分别为31.41%、31.11%和51.07%,配对样本t检验表明,MFCDD下的聚类准确率优于DTW和LCSS,置信度为99%。与LCSS和DTW方法相比,基于MFCDD的k-medoids聚类可以更好地识别数据集的正确聚类数目,运行时间更短。此外,依据DTW、LCSS和MFCDD方法下确定的最佳的聚类中心对实验数据集进行分组,平均分类准确率分别为27.32%、40.23%和47.39%,MFCDD在确定聚类中心方面有更好的性能,置信度至少为85%。总的来说,基于LHFDWT和MFCDD的k-medoids聚类技术在确定聚类数目、聚类中心和搜索效率、聚类准确率方面,效果均得到了显著提升,证明了本文所提的相似性搜索算法的优越性。

本文的结论具有重要的理论意义和现实意义。在理论方面,基于LHFDWT和MFCDD的相似性搜索算法在时间序列聚类中的良好表现改进了现有方法的不足,完善了TSDM中时序降维和相似性度量关键问题的技术基础。在现实方面,如通过聚类识别金融资产的不同类别对资产组合管理具有重要意义。另外,还可以应用于预测等任务,这将在后续研究中继续探索。由于目前还没有适用于所有类型数据集的相似性度量方法,因此在今后的研究中可以探讨应用模糊逻辑方法来度量时间序列相似度的可行性。