海洋立管浪致疲劳损伤及其对结构疲劳寿命的影响
2023-01-07谷伟
谷 伟
(中海油能源发展股份有限公司采油服务分公司 天津300452)
0 引 言
随着深海装备的研发及海洋油气产业的发展,多种形式的海底管线和海洋平台投入使用[1]。海洋立管作为平台与海底管道的连接通道,服役于恶劣海况,其露出海面的部分承受海风的直接作用,水下部分承受波浪、海流的持续冲击,受力形式复杂,极易发生失效[2-4],进而会导致巨大的财产损失,甚至污染海洋环境。由于立管的弹塑性变形、模型的疲劳损伤分析等都属于非线性问题,且其失效形式和失效影响因素是多样的,导致海洋立管的破坏机理分析及风险评估十分困难。海洋立管在海洋环境中承受随时间变化的波浪及海流作用,分析其应力和变形不仅需要进行静力计算,同时还要进行动力学方面的分析[5]。由于动力学分析考虑了由质量、阻尼和流体的加速度引起的时变效应,结构的应力、位移、变形等参数不但是与空间坐标有关的函数,同时与时间坐标也有关系,比静力学增加了时间变量。因此,动力问题控制方程的求解难度大为增加[6]。
波激振动是导致浅海平台立管疲劳失效的主要原因[7],对立管进行时域损伤分析和研究其疲劳失效机理具有重要意义。
1 有限元模型建立
本文针对渤海湾某导管架平台立管进行研究,其所在海域作业水深为 20m,该海域海底表层土壤为粉质黏土,泊松比µ取0.45,设计抗剪强度为4kPa,工作内压为 10MPa,正常和极限工况风速及波浪情况如表1所示。

表1 风速、波浪参数表Tab.1 Wind speed and wave parameters
利用有限元软件 ANSYS对海洋立管结构进行分析计算,选择 PIPE59单元对立管进行模拟[8]。建模时选择管材为 X65钢,弹性模量 210GPa,泊松比0.3,屈服极限 450MPa。选择水深 15m,海面以上竖管长度取为10m,立管外径273mm,壁厚12mm,弯管半径取为 1.2m(按设计要求取约 4倍管径),水平管长度为30m,并假定距弯管底端20m处入泥建立模型,根据现场经验,分别选择海面处以及海面以上3、6m 处、海面以下 3m处布置管卡。该海域海水密度 1025kg/m3,管内流体密度 1250kg/m3。建模时,泥线以上立管采用 PIPE59单元,且坐标原点选定在海面处。水平入泥管段模拟为 PIPE20单元,管土相互作用采用 COMBIN39单元模拟[9],土壤压力由式(1)确定。
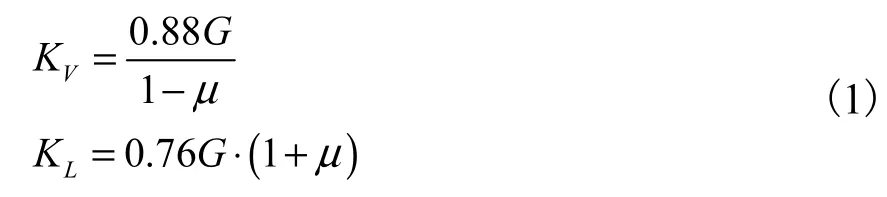
式中:KV为竖向土弹簧刚度,N/m;KL为横向土弹簧刚度,N/m;G 为土体剪切模量,Pa;μ为土体泊松比。
竖向弹簧刚度系数为 6400N/m,横向弹簧刚度系数 4408N/m。边界条件设置为立管顶部简支和水平管远端固支。建立海洋立管力学分析模型和有限元模型如图1、2所示。
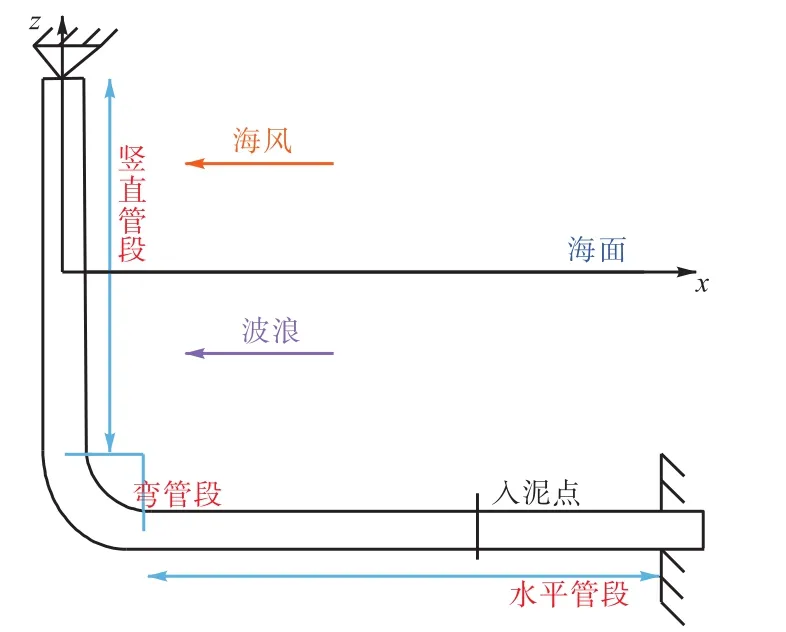
图1 海洋立管系统力学模型Fig.1 Mechanical model of riser system
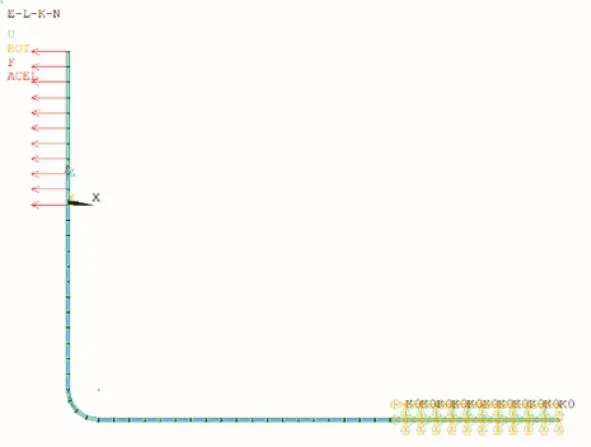
图2 海洋立管系统有限元模型Fig.2 Finite element model of riser system
2 波浪力静力分析
海洋工程结构所承受波浪力的大小受波浪相位角的深刻影响,相位角反映了正弦形式简化的波浪力的波形特征。本节进行海洋立管结构的静力分析时,为保证结构安全,选择了最危险工况作为载荷环境,即假定波浪以某一相位的最大作用力形式作用于立管。进行静力分析之前编写相位角搜索程序,对耦合作用的波浪力进行 0°到 360°的相位搜索,寻找某一相位角使得波浪力曲线恰好位于最高点,即出现最大波流力。首先建立波浪相位角搜索程序,相位角留空作为输入条件,获取如图3所示海面处立管节点的波浪力与相位角的作用关系曲线,得到最大波流力作用时的相位角为 42°,以其作为输入条件,得到立管结构的等效应力分布云图和节点位移云图。

图3 波浪力-相位角关系曲线Fig.3 Wave force-phase angle relationship curve
由云图可知:运行工况下立管结构的最大应力为65.3MPa,出现在弯管段中部;最大位移为13.765mm,出现在竖直管段底部。
3 疲劳损伤时域分析
3.1 浪致疲劳理论
工程构件在一段时间交变应力的作用后发生断裂的现象称为疲劳破坏,导致疲劳破坏的交变载荷称为疲劳载荷[10]。对海洋立管结构而言,在服役海域中抵抗波浪、海流等交变循环荷载的能力就是海洋立管的疲劳强度,其承受上述荷载的循环次数就是立管的疲劳寿命。由前述分析可知,常规载荷在立管结构中所引起的应力均小于材料的屈服强度,因而在疲劳分析中属于应力疲劳失效范畴。故选取工程中常用的S-N曲线表征结构的疲劳强度,S代表作用于工程结构的交变应力的变化范围;N代表恒幅载荷作用下,结构达到破坏时的应力循环次数,即疲劳寿命[11]。根据SY/T 10030规范,S-N曲线的数学表达式如式(2)所示。

式中:ΔS为应力幅;ΔSref为循环次数等于 2×106时的应力幅;M为双对数斜率的倒数。
3.2 时域响应分析
基于静力分析模型,利用ANSYS模态分析模块得到立管系统六阶自振频率,如表2所示。

表2 立管自振频率计算表Tab.2 Natural frequency of marine riser system
利用 ANSYS瞬态动力学模块对其进行时域响应分析[12]。时程分析取作用时间 100s,时间间隔0.2s。根据模态分析所得到的第一、第二阶固有频率计算得到作为输入参量的结构阻尼系数:α=0.071,β=0.00389。本节在对立管结构进行瞬态动力学分析时仅考虑波浪载荷的水动力效应而忽略其他的作用效果,故设置波流耦合力的相位角为 0°,分别计算竖直管、弯管、水平管段的稳定应力幅,利用Goodman曲线修正,进而获取各单元的等效应力幅值,其随立管高度的分布规律如图4所示。为便于分析,划分单元时自立管顶端到底端分别为1~28号单元,其中竖直管段包含 1~22号单元、弯管段包含23~28号单元。
由图4可知,随高度降低,立管竖直段等效应力幅逐渐减小,弯管段应力幅逐渐增大;应力幅最大值出现在立管弯管段底部,立管竖直管顶部和弯管底部均为疲劳危险位置,其与静力计算应力危险位置并不相同。因此,仅对静力失效点进行补强无法避免立管的疲劳破坏。
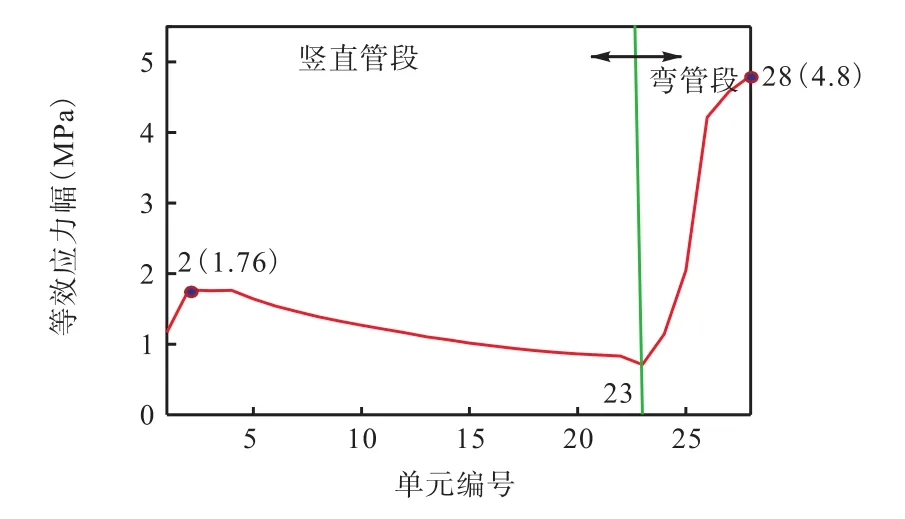
图4 立管各单元等效应力幅分布图Fig.4 Equivalent stress amplitude distribution diagram of riser elements
3.3 管卡类型的影响
浅海平台立管主要有导向卡和悬挂法兰 2种管卡类型[13],由于其结构形式不同,对立管的约束程度也不同。一般来说,导向卡和立管之间留有一定间隙,故在位期间仅约束立管的横向位移,而允许其沿轴向自由滑动,悬挂法兰则能够限制其轴向移动。分别针对该2种类型管卡建立模型,获取不同约束条件下立管弯管底端的等效应力幅值,结果表明仅考虑波浪来流方向的作用力时,管卡类型对危险点的疲劳损伤影响不大。
当选用导向卡约束时,即仅限制立管结构横向振动位移时,结构弱点的应力时间历程曲线如图5、6所示。

图5 2号单元稳定应力幅Fig.5 Stable stress amplitude of element 2
当选用可约束轴向位移管卡时,上述2处位置点的应力时程曲线如图9、10所示。
3.4 弯管半径的影响
立管弯管段在周期性波浪力的作用下容易产生疲劳失效,本节分析改变弯管半径时结构疲劳寿命的变化规律。按设计要求,弯管的弯曲半径为 3倍管材直径或 5倍管材直径[14]。本节分别计算弯管半径为3D、4D、5D 时(图9、图10),弯管底部位置的应力时程响应,最终得到不同弯管半径底部单元应力幅,如表3所示。基于表中数据,可明确弯管半径的改变对立管结构疲劳寿命的影响规律,从而为指导工程现场立管弯管的选型安装提供分析基础。

表3 不同弯管半径底部单元应力幅Tab.3 Stress amplitude of bottom element of different elbow radius
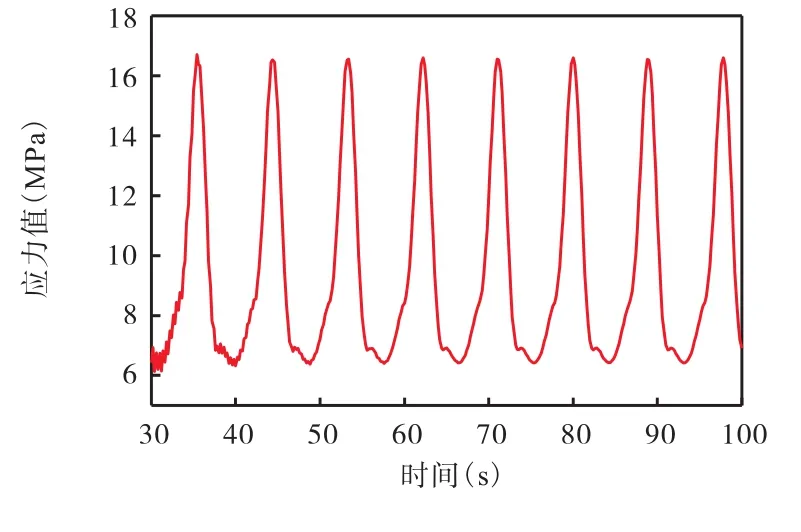
图9 弯管半径取3DFig.9 Elbow radius taken as 3D

图10 弯管半径取5DFig.10 Elbow radius taken as 5D
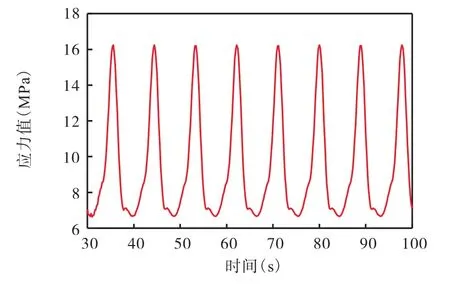
图6 28号单元稳定应力幅Fig.6 Stable stress amplitude of element 28
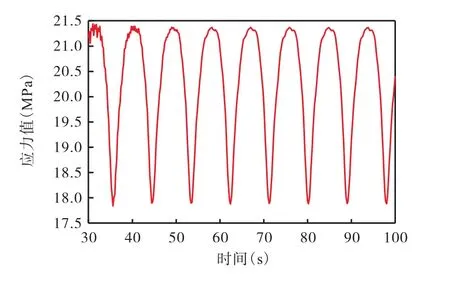
图7 2号单元稳定应力幅Fig.7 Stable stress amplitude of element 2

图8 28号单元稳定应力幅Fig.8 Stable stress amplitude of element 28
由计算结果可知,弯管半径越大,其底部单元等效应力幅值越大,即寿命越短。故应在满足工程要求的前提下,尽可能选择弯管半径较小的立管结构,这一做法有助于提高使用年限。
3.5 管卡分布位置的影响
本节研究管卡不同分布位置对立管疲劳寿命的影响。分别针对 4套不同的分布形式计算弯管底部的时域响应,研究最优的管卡排布方式。以海面处坐标为 0,4个管卡分布在海面上下不同位置处时,海洋立管结构的等效应力幅值分布情况如表4所示,其反映了不同管卡分布形式下海洋立管结构的疲劳寿命变化趋势。据此,可寻找海域环境中海管管卡的最优排布形式。
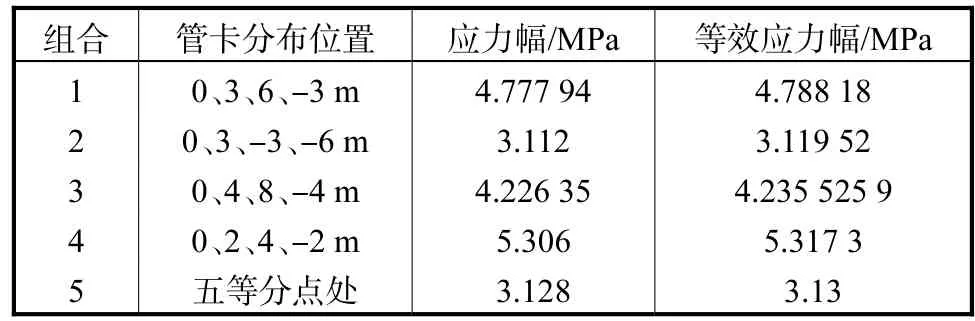
表4 不同管卡分布位置立管底部单元的应力幅Tab.4 Stress amplitude of bottom element of riser at different clamp distribution positions
上述结果表明在立管长度等分点处布置管卡并非最优选择。管卡分布间距越小,立管弯管底部等效应力幅越大,即疲劳寿命越短;相同分布间距,管卡距离底部越近,立管疲劳寿命越长。
4 结 论
本文以渤海平台桩腿立管为研究对象,选取该海域特征波浪参数,利用ANSYS软件对其进行了疲劳损伤时域分析,探究了立管结构的疲劳失效机理,分析了管卡类型、弯管半径和管卡分布形式对立管疲劳寿命的影响。根据本文的研究可得到以下结论:
①随高度降低,立管竖直段等效应力幅逐渐减小,弯管段应力幅逐渐增大,应力幅最大值出现在立管弯管段底部,即此处容易发生疲劳破坏;
②仅考虑来流方向振动时,管卡类型对立管结构的疲劳寿命没有影响;
③减小弯管半径有助于降低结构弱点的交变应力幅和提高立管使用年限,故建议选择弯管半径为3倍管径的立管类型;
④相同管卡数量和分布间距前提下,管卡距离底部越近,立管疲劳寿命越长;
⑤本文给出一套管卡布置方案为,海面处设置1个、海面以下设置2个、海面以上设置1个,此法能最大限度延长立管使用寿命。
