镧系离子间无辐射能量传递速率的教程综述

1 Introduction

Energy transfer（ET）processes are ubiquitous in nature and are essential to life[1-2].Despite being difficult to visualize,these ET processes are always present in our everyday life and obey the laws of thermodynamics（for macroscopic systems）.Many modern technologies are based on ET processes,for instance,those involving luminescence,where an excited sensitizer transfers energy to an activator that emits light（or electromagnetic radiation）.Most results of these ET processes are visible and quantifiable,but their detailed understanding and description,at the microscopic level,requires quantum mechanics.As a result,at least two concepts are important,namely,（quantum）states and transitions between these states.

Photoluminescence involving lanthanide ions has some unique and remarkable features,which have been explored in many applications and new technologies,from biomedicine to engineering,and public health to public safety[3-7].Energy transfer between lanthanide ions is particularly relevant to several processes such as long-range energy migration and energy upconversion.Resonances present in systems containing lanthanide ions of the same type,e.g.,Yb（Ⅲ）,allow the energy to be efficiently transferred between these ions,which can migrate for long distances depending on their concentration and the host matrix[8-11].On the other hand,a lanthanide ion with relatively large oscillator strength,e.g.,Yb（Ⅲ）and Nd（Ⅲ）,can be employed as a sensitizer of another lanthanide ion,e.g.,Er（Ⅲ）and Tm（Ⅲ）,called an activator,which can be excited by sequential energy transfer processes,followed by emission of photons with higher energy than those absorbed photons;hence energy upconversion[10,12-13].In this context,energy transfer between lanthanide ions（Ln-LnET）plays a fundamental and essential role in several processes that are explored and exploited in applications and new technologies[14-16].Therefore,the focus of this contribution will be the quantitative description of theLn-LnET processes.

A common picture used for a general ET process employs two subsystems denoted as donor（D）and acceptor（A）.Initially,the donor is prepared in an excited state,D*,by absorbing energy（light,heat,and mechanical）,which may be represented as=.In other words,in the initial state,the energy absorbed by the system is localized at the donor subunit.Then,the system undergoes a transition to another state with the energy localized at the acceptor subsystem,represented as.This general description requires some clarification and specification of different categories of ET processes as well as additional phenomena accompanying these processes.For instance,energy transfer can induce or be caused by electron（or charge）transfer between the subsystems.These coupled processes are important and relevant for many biological systems and applications,but they will not be considered here.The ET processes of interest are uncoupled energy transfer processes in the sense that are not caused nor can induce electron transfer.This is an important distinction that is not always clear in the literature and has caused some confusion.

The transition mentioned above describes an ET process,represented by,can be pictured as a deexcitation of the donor and an excitation of the acceptor,which may or may not involve photon（s）.When the deexcitation ofD*occurs by photon emission（with energyћω=hν）,+hν,and the emitted photon is absorbed byA,+hν,then the ET fromD*toAis known as radiative energy transfer.This is also an important category of ET processes;however,they are usually not operative when the acceptor（or activator）is a lanthanide ion.This is because the oscillator strengths associated with 4f-4f transitions are very small（～10-6）[17-19],except for some transitions in Nd（Ⅲ）and Yb（Ⅲ）,which preclude radiative absorption.Thus,for those interested in lanthanide ions,the dominant ET processes are nonradiative（or radiationless）.Recently,the intramolecular ET processes in lanthanide complexes,namely,ligand-Ln（Ⅲ）transfer rates,were revised and reviewed[20].Thus,the present review will focus on radiationless or nonradiative ET processes between lanthanide ions,Ln-Ln.

The main goal is to present a review for nonspecialists,providing sufficient concepts to critically ascertain the approximations involved in the equations of the energy transfer rate mechanisms.Enough details will be provided for a qualitative assessment of the main factors affecting the ET processes inLn-Lnsystems as well as to perform estimations and calculations of these ET rates.The original equations were reorganized to ease their applications as well as their interpretations.In the Supporting Information,a derivation of Fermi's golden rule is provided together with the physical constants and unit conversions,details matrix elements calculations,and dimensional analysis of the main quantities.

In the following sections,some concepts and equations involved in the quantum treatment of transitions will be present culminating in Fermi's golden rule for transition rates.This expression will then be particularized for nonradiative transitions between two lanthanide ions,namely,theLn-Lnenergy transfer rates.Detailed applications of these equations will be presented as tutorial examples for ET processes involved in the Yb（Ⅲ）-Er（Ⅲ）and Tb（Ⅲ）-Eu（Ⅲ）pairs.

2 Quantum Transitions

An energy transfer process can be regarded as a transition from a state representing the energy localized initially at the donor subsystem to another state characterized by the energy localized in the acceptor unit.This process can be described quantitatively by an energy transfer rate,that is,the probability of transition induced by a perturbation per unit of time,in units of s-1,because the probability is dimensionless.Thus,to comprehend the equations for the ET rates,representations of the initial and final states are required,which will be addressed in detail later,as well as the transition probability between these states per unit of time.

For most transitions occurring at the molecular level,their rates can be quantitatively described by Fermi's golden rule.A detailed derivation of the expression for the transition rate,in particular Fermi's golden rule,can be found in many textbooks[21-22]and is provided in the Supporting Information.Here we will present the main equations and the approximations and assumptions employed.

Transitions at the molecular level are described by quantum mechanics.A system is described by its state represented by a（vector）state or wavefunction,which depends on the spatial and spin coordinates of its particles and on the timet.This state can be expressed as a linear combination of a complete set of eigenfunctions{Ψn(t)}with corresponding energy eigenvalues{En}.

If the system is described by a time-independent Hamiltonian,e.g.,a molecule with contributions from the kinetic energy of the nuclei and electrons and Coulomb interactions between the charged particles（nuclei-nuclei,nuclei-electrons,and electrons-electrons）,the time-dependent Schrödinger equation can be separated and have solutions,whereψnare the stationary（timeindependent）eigenfunctions of this Hamiltonian.So,if the system is（prepared）at an eigenstateΨm,with energyEm,then it is stationary,=constant,and it will remain in this state indefinitely.Thus,a perturbationis needed to promote a transition from this state to another state.This perturbation causes the temporal evolution of a non-stationary stateΨ(t),which can still be represented as a linear combination of eigenfunctions{Ψn(t)}with coefficients{cn(t)}.As a result,the probability of finding the system at timetin statekis.

As a result of this perturbation,the system can be described by a Hamiltonian,̂,consisting of the time-independent Hamiltonian,Ĥ0,and the perturbation,i.e.,.A procedure developed by Dirac starts by replacing the wavefunctionΨ(t),in the time-dependent Schrödinger equation employinĝ,by an expansion in terms of{Ψn(t)}and{cn(t)}.After applying the time derivative and the full Hamiltonian̂on this expansion and projecting the resulting equation onto statek（‘multiplication’or scalar product with the bra,an exact equation for the time evolutionċn(t)is obtained.By integrating the resulting equation fromt=0,when the coefficients arecn(0),to the timetof interest,an exact expression for the coefficientscn(t)is derived,so the probability could,in principle,be calculated.Thus,a uniquely define exact solution is obtained when the boundary conditions,namely,the initial coefficientscn(0)are known.These conditions are usually expressed ascn(t=0)=δni,whereiis the initial state,orci(t=0)=1 and=0.

However,the exact determination of the coefficientck(t)requires all the coefficients,includingck(t),i.e.,the exact solution is a set of coupled integral equations.So,approximations and assumptions are needed to obtain a computable expression.

Suppose that the perturbation is so weak and applied during a time interval so short that all the coefficients remain close to their initial values and are approximated ascn(t)≅0 forn≠iandci(t)≅1.This is the so-called first-order perturbation or firstorder approximation and yields the following expression for the coefficients（k≠i）at timet[21-22]:

whereωki=(Ek-Ei)ћand the generic matrix element,Vkn,of the perturbation operator̂is expressed as

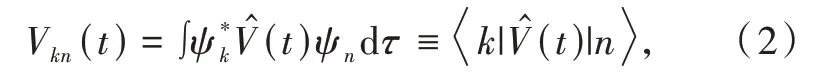
with the respect to the stationary eigenfunctionsψkandψn.Notice that the first equality employs the integral representation of the matrix element,which is equivalent to that in the‘bra-ket’（or Dirac）notation.

3 Fermi’s Golden Rule for Radiationless（or Nonradiative）Transitions

Several processes are induced by a coupling between subsystems or between states and radiation is not required,representing the so-called radiationless or nonradiative transitions.For example,in a timet=0 the system（instantaneously）absorbs energy（e.g.,light absorption,mechanical or thermal excitations）and is promoted to an excited state,thus initiating a coupling or interaction.This is the initial condition of the system,and this excited state is its initial statei.The nonadiabatic electronic coupling or the spin-orbit coupling between the initial stateiand another statekcauses a radiationless transition fromitok,i→k.Another example is a system of two uncoupled subunits,e.g.,donor and acceptorDA.Upon excitation,att=0,localized on the donor subsystem,the system can be represented asD*-Aand a coupling or interaction betweenDandAappears and promotes a nonradiative transition to another state that can lead to energy transfer or electron transfer,depending on the nature of the donor and acceptor,and on the initial and final states.In these radiationless transitions,the coupling or interaction initiated att=0 does not depend explicitly on time,so it is constant in time:̂=constant.

Thus,for nonradiative energy transfer processes,a constant perturbation̂（time-independent）is considered,which is turned on att=0 and off att=τ.For this perturbation,the coefficient describing statekat timet≥τbecomes[21]:

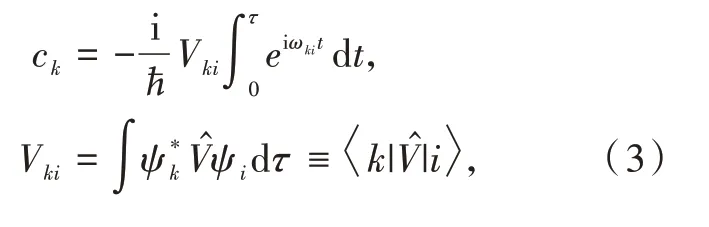
where it was considered that the matrix elementVkihas a weak dependence on the quasi-continuum states aroundk.The duration of the perturbation,denoted asτ,should not be confused with the lifetime of an excited state,which is usually also denoted asτ.

The integral can be performed analytically,so the transition probability to statekis

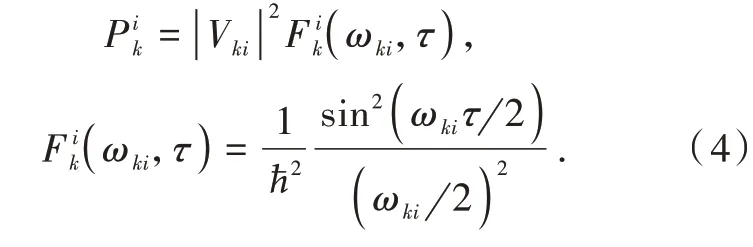
This expression yields the same probability for the reverse transition:,becauseand.

Forτ≳2πℏEk,the functionbecomes sharply peaked,with the height of the peak aroundEkincreasing asτ2/ћ2and width decreasing as 2πћ/τ,so the area of this peak is approximately 2πτ/ћ,which grows linearly withτ.This indicates that a timeτafter the initial coupling（or interaction）between the states or the subsystems,their energy eigenvalues will present dispersions ofδE=2π/ℏτ,which is consistent with the energy-time uncertainty principle becauseδEτ=2πћ＞ћ/2[21].So,the final states after the perturbation are better described as nearly a continuum of energy values with a narrow distribution represented by a density of states,ρ(E),which is the number of states per energy unit around energyEandρ(E)dEis the number of（continuum）states in the rangeEtoE+dE[21-22].In other words,the perturbation,represented by the interaction（or coupling）,has generated many final states closely spaced in energy.For a molecular system,other mechanisms of energy dispersion will also be present,such as a distribution of closely spaced rotational-vibrational energy levels.Thus,if the final states have a density of statesρ(E),then the total probability of transition to statekbecomes an integral of(E)dEover all final states accessible under the influence of the perturbation:

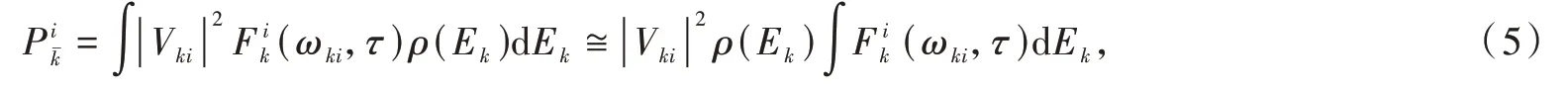
where the last approximation considers that the matrix elementVkiand the density of stateρ(Ek)are constant in the integration range.Because the functionis sharply peaked,the integrand has significant values only aroundEk,which justifies the last approximation.This property of the functionalso allows for extending the integration from-∞to+∞,so the last integral is just 2πτ/ℏandhas a linear dependence onτ,whererepresents the summation over over the quasi-continuum（e.g.,rovibrational）contributions..As a result,the transition rateWi→k≡Wkifrom an initial stateito a final statek,which is the change of the probability per unit of time,can be written as[21-22]：electromagnetic radiation.

For a proper application of this expression for the transition rate,it is important to present the approximations and assumptions as well as their consequences（see Supporting Information）.

The task of applying Eq.（6）to a given process becomes（ⅰ）the proper representation of the initial and final states of the system,（ⅱ）defining and establishing the perturbation,and（ⅲ）determining the density of states.

The sharply peaked function

This is called Fermi’s golden rule and provides the rate of transition.

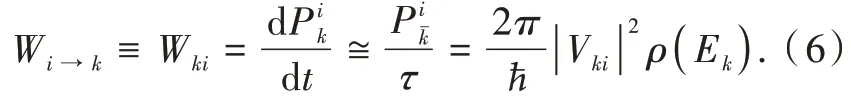
Despite this derivation being performed for constant perturbation,the same expression is obtained for periodic potentials that describe,for instance,theappearing in Eq.（5）becomes a Dirac delta function at theτ→∞limit.As a result,the density of statesρ(Ek)in Eq.（6）can be replaced by the delta functionδ(Ek-Ei)for longτ[21-22]:

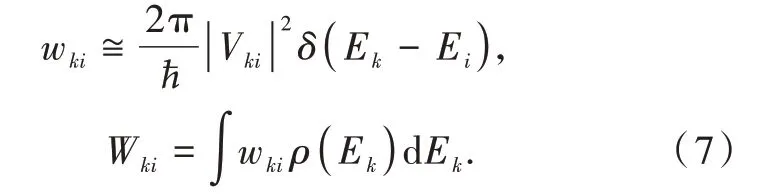
This expression is known as state-to-state Fermi's golden rule.The delta functionδ(Ek-Ei)expresses the condition that at theτ→∞limit,only transitions that satisfy energy conservation can be caused by a secular（time-independent）interaction.The presence ofδ(Ek-Ei)in Eq.（7）does not violate the energy-time uncertainty principle,because asτ→∞,the energy dispersionδE=vanishes.

4 Rates of Energy Transfer Processes

As mentioned,the application of Eq.（6）for an energy transfer process between a donor and acceptor D-A requires the proper representation of the initial and final states.Usually,the subsystems D and A are considered uncoupled or weakly coupled,so that the state of the system can be represented by a（tensor）product of wavefunctions describing the subunits,namely,.In this representation,the wavefunctionΨAdepends on the spatial and spin coordinates of the nuclei and electrons constituting the acceptor and similarlyΨDthe donor.Despite this simple notation,ΨDandΨArepresent multielectronic states that may require more than one determinant（multideterminantal）for an adequate description.Employing a single particle or monoelectronic representation may lead to improper descriptions and an unreliable picture of the energy transfer process.

Because the D-A subunits are considered independent,the perturbation can be promptly and easily pictured as the interaction between these subsystems.So,the perturbation̂can be represented by the Coulomb（or electrostatic）interactions between electron densities and nuclear charges of the donor and the acceptor.This perturbation leads to a mechanism known as multipolar[23]or,more restricted,dipolar or Förster[24].On the other hand,approximating the wavefunction of the system by a（tensor）product causes the electrons of the donor to be distinguishable from the electrons of the acceptor,which violates the indistinguishability and antisymmetry principles of quantum mechanics.So,the exchanges between the electrons of the donor and the acceptor can be regarded as a perturbation of the D-A subunits.This perturbation can be described by an exchange operator and originates a mechanism known as exchange or Dexter[25].

A step further in the development of a workable expression for the energy transfer rate can be taken by realizing that,usually,the time scale of the nuclear motion is much longer than of the electronic motion.As a result,the molecular wavefunction can be approximately factored into a product of electronic and nuclear wavefunctions.This is the well-known Born-Oppenheimer approximation,which has been used since the dawn of quantum mechanics and its successes and limitations are well-established[26-27].So,the wavefunctions describing the initial state with the energy localized at the donor,,and the final state related to the energy localized at the acceptor,,can be approximated as

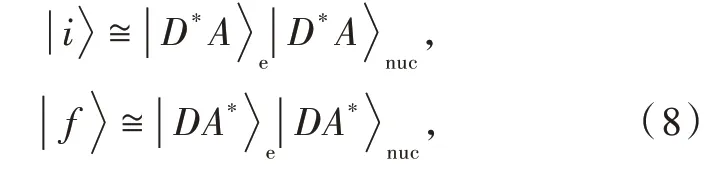
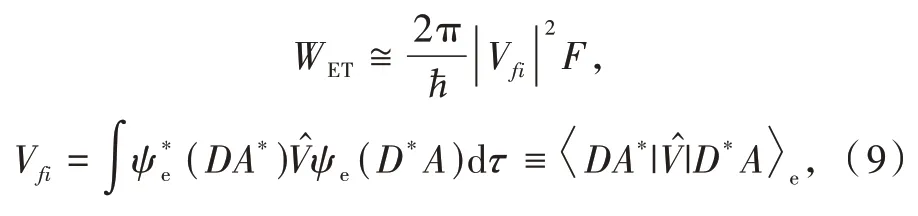
whereVfiis the electronic matrix element due to the time-independent part̂of the perturbation operator,while theF-factor includes contributions from the overlap of the nuclear wavefunctions,·,and from the density of statesρ(E).This separation into an electronic contributionVfiand aF-factor is possible only if the time-independent perturbation̂acts in the electronic（spatial and spin）coordinates,soVfiis a function of the nuclear positionsRα,Vfi≡Vfi({Rα}).Notice that in the wavefunction representation of the matrix element,the notationrepresents the complex conjugate of the functionψe,whereasDA*orD*Arepresents the acceptor or the donor in an excited electronic state.This confusion does not arise in the‘bra-ket’notation.

So far,the proposed model,expressed in Eq.（9）,to describe energy transfer processes is general and can be applied to intermolecular D…A organic and/or inorganic pairs[28-29]as well as energy transfer in intramolecular D-A pair such as lanthanide complexes L-Ln（ligand-lanthanide ion）[20,30-33]and lanthanide-lanthanide ion pairs LnD-LnA[34-37].For the latter case,it is important to distinguish two situations:LnD-L-LnA,when there are bridging ligands between the lanthanide ions;andLnD-LnA,when no ligands bridge the ions.The case ofLnD-L-LnAwill not be considered here because the direct energy transfer pathways between the lanthanide ions are very inefficient compared to the ligand-lanthanide energy transfer pathways.So,most likely this case involves nonradiative energy transfer processes between the ligands and the lanthanide ions.Recently,the theoretical modeling of intramolecular ligand-lanthanide energy transfer was reviewed[20].So,here the focus will be on the direct energy transfer inLnD-LnApairs with no bridging ligands will be described.

5 Energy Transfer Rates Between Lanthanide Ions

A quantitative description of the nonradiative energy transfer between lanthanide ions（Ln-LnET）was developed in the early 1970s[38],after the success of the Judd-Ofelt theory for the 4f-4f transition intensities[39-40]and way before the development of the ligand-lanthanide ET model[20,32,41].This sequence of events may be explained by the very similar nature of the donor and acceptor states in theLn-LnET,in contrast to the very dissimilar nature of the states involved in ligand-lanthanide ET.Lanthanide ions have a unique feature related to the shielding of theNelectrons in the 4f subshell,4fN.Because the filled subshells 5s25p6are more radially external than the 4fNsubshell,the electronic density of 5s25p6shields the 4f electrons from the interactions with the surroundings（e.g.,ligating atoms,ligands,ions,lattice,solvent,etc.）of the lanthanide.As a result,the 4f states are practically those of the freeion,where the effects of the surroundings can be treated as a small perturbation,if necessary.This feature was explored in the development of the Judd-Ofelt theory,and the successes of this formulation validate this picture of the 4f states.Therefore,donor and acceptor states in the energy transfer processes between 4f levels of lanthanide ions are well-defined and several theoretical tools developed previously could be employed.TheseLn-LnET processes can be pictured as an excited state within the 4fNDconfiguration of the donor lanthanide being deexcited to a lower level（usually the ground state）and its energy is transferred to the acceptor lanthanide causing an excitation within its 4fNconfiguration.Because the 4f donor and acceptor states are well localized on each lanthanide,the donor-acceptor distance is taken as the distance between the lanthanide ions.This feature is not present in a ligand-Lnsystem,because the states of the ligand are usually delocalized,the donor-acceptor distance is much more difficult to define and determine.

Because of the localized nature of the 4f states,the donor and acceptor electronic wavefunctions can be approximately treated as independent or uncoupled,that is,

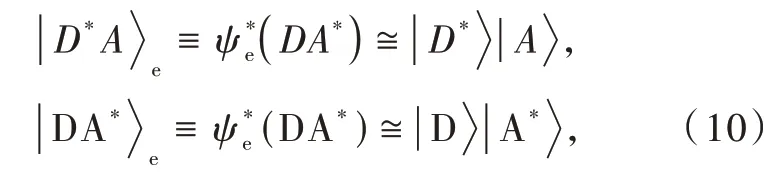
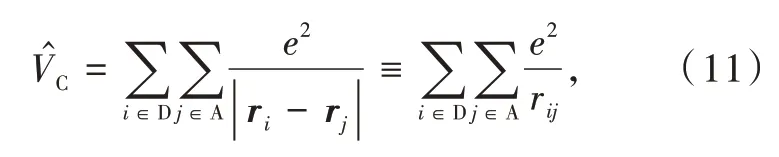
whereriandrjare the position vectors of electronsi（belonging to the donor）andj（belonging to the acceptor）,respectively.

Another more subtle interaction comes from the principles of quantum mechanics,which has no classical analogue.In the approximation expressed by Eq.（10）,it is implicitly assumed that the donor has a fixed number of electrons,e.g.,ND,as well as the acceptor hasNA-electrons.However,when these subsystems interact with each other,the electrons of the donor must become indistinguishable from the electrons of the acceptor,as a principle of quantum mechanics.This can be accomplished by an exchange operator that permutes the indices（or labels）of each electron of the donor with each electron of the acceptor,which can be represented by the following operator

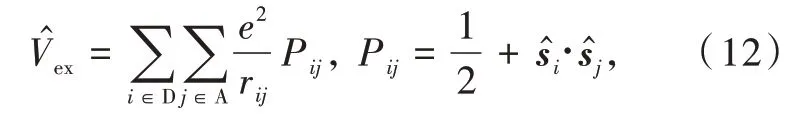
wherê and̂ are the spin operators of electronsiandj.It is important to realize that the wavefunctions of the isolated donor and acceptor are normalized and antisymmetrized,so they individually satisfy the principles of quantum mechanics.

The electronic wavefunctions of 4f states of an isolated lanthanide ion are accurately described by the total electronic angular momentum quantum numberJand additional quantum numbersψ.Thus,the initialand finalstates,Eq.（10）,in the ET process are represented asNotice that the projectionMJof the angular momentumJis also an appropriate quantum number.In addition,it is possible to represent these wavefunctions as a linear combination of the wavefunctions represented in the total spinSand orbitalLangular momenta（and their projections,MSandML）basis as the so-called intermediate coupling scheme.This transformation is quite convenient because it allows the choice of a diagonal matrix representation of the operator of interest.

Once the wavefunctions describing the initial and final states have been properly represented,the matrix element involving the perturbation operatorcan be determined.Notice that this operator involves the two-electron interactione2/r12,which can be expanded in terms of the spherical harmonics or equivalently in terms of Racah's irreducible spherical tensor operators[23,42].This allows the factorization of the matrix element into radial and angular parts,where this latter part can be calculated analytically.As a result,the following equations for the energy transfer rates between lanthanide ions can be obtained[16,34-37,43]and classified the dipole-dipole,Wd-d

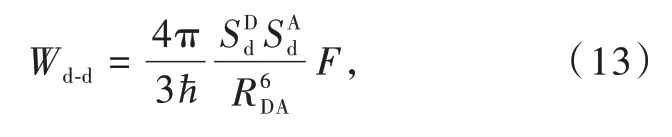
the dipole-quadrupole and quadrupole-dipole,Wdq-qd,

the quadrupole-quadrupole,Wq-q,

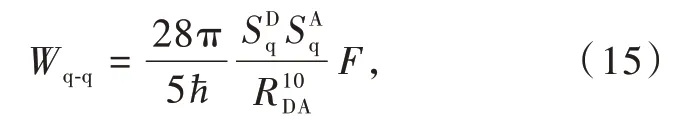
the magnetic dipole-magnetic dipoleWmd-md,

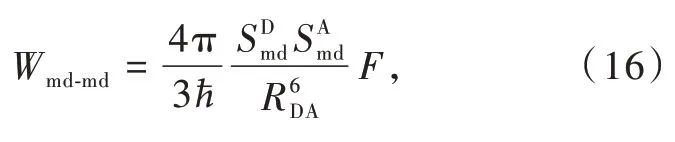
and the exchange,Wex,mechanisms

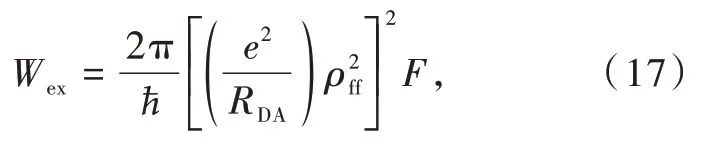
whereSd（in erg·cm3）is the modified forced electric dipole strength

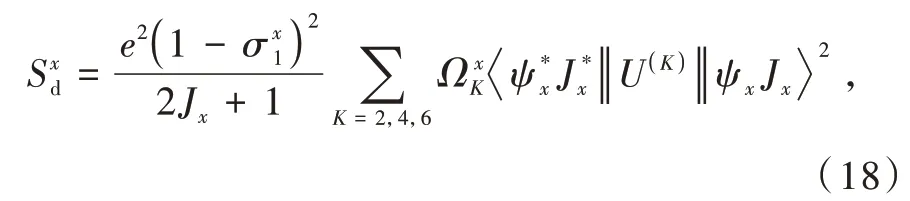
whileSq（in erg·cm5）is the modified quadrupole strength

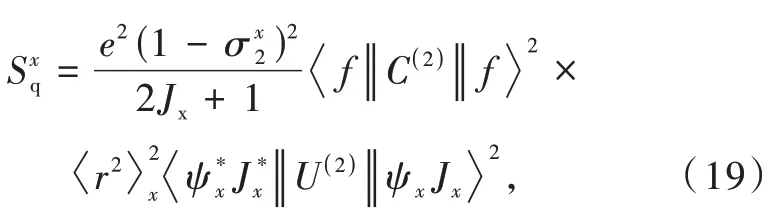
whereasSmd（in erg·cm3）is the magnetic dipole strength analogue

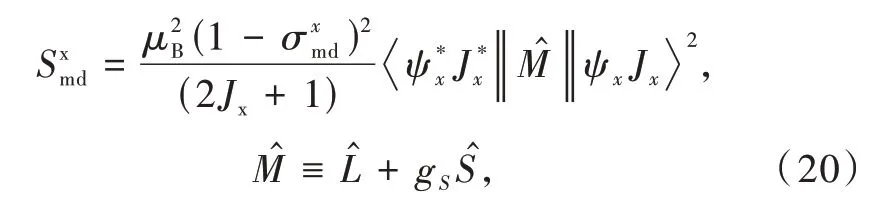
withx=A for the acceptor andx=D for the donor,Jx=being the total angular momentum quantum number of the excited state of the donor orJx=JAof the ground state of the acceptor,andgS=2.002 319 3 being the electron sping-factor[44].See the Supporting Information for dimensional analysis and unit conversion.

The total energy transfer rate will be a summation of each contribution in Eqs.（13）-（17）.Usually,there is one contribution that dominates this sum,however,there are exceptions,and the relative contributions change strongly with the donor-acceptor distance,RDA.

It is important to emphasize thatSdis denoted asforced electricdipole strength analogue because

only the forced electric dipole（FED）mechanism contributes to the calculation ofΩK.This is due to the contribution of the opposite parity configuration mixing by the odd components of the ligand field to the intensity parametersΩK,like in the Judd-Ofelt theory[38].

These equations are the same as those published in the revisited versions of the energy transfer rates between lanthanide ions[34,36-37].However,those involving multipole and magnetic dipole mechanisms were rearranged and separated into more symmetrical and easily interpretable forms.In addition,these separations allow a stepwise calculation of the contributing terms,which can assist the analysis of the transfer rates and determine if there are dominant contributions from either donor or acceptor.

The energy transfer rates are expressed in terms of well-defined and calculable quantities.It must be emphasized that the choice of the two-electron interaction ase2/r12,implies that the CGS system of units is employed.The quantities in these expressions depend on physical constants and other properties independent of the nature of the lanthanide ion:

·ℏ=h/(2π)is the reduced Planck constant（see the Supporting Information for the values of the physical constants and unit conversion）,

·eis the elementary charge in esu,

·μB=eћ/(2mec)is the Bohr magneton,

·ΩK≡ΩK(FED)is the forced electric dipole contribution to the intensity parameter of rankK,in units of 10-20cm2[20,34,36],

on the surroundings of the lanthanide ion:

·(1-σk),withk=1 and 2,is the shielding factor for donor and acceptor approximated as[34,53-54]

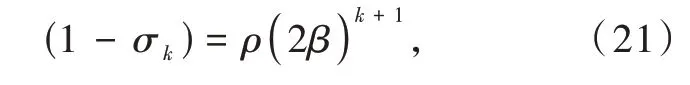
whereρis the overlap integral between the valence subshells of the ligating atom and the 4f subshell of the lanthanide ion andβ=1( 1±ρ)[53,55],

·σmdis the shielding factor,for donor and acceptor,which shields the magnetic dipole interactions,

on the lanthanide pair:

·RDAis the distance between the lanthanides,

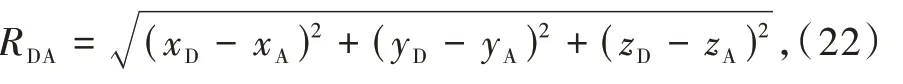
with(xD,yD,zD)and(xA,yA,zA)being the Cartesian coordinates of the donor and acceptor centers,respectively,

·ρffis the overlap integral between the 4f subshells of the donor and acceptor lanthanide ions[53].

The last quantity to determine the ET transfer rates is theF-factor in Eq.（9）,which includes contributions from the nuclear wavefunctions and the density of states.It is important to recall that when the donor subunit is excited to generate the initial state in the energy transfer process,the energy eigenvalues will be broadened and will have a quasi-continuum behavior that is described by the density of states of the donorρD(E)and of the acceptorρA(E).In the original model for the nonradiative energy transfer between organic speciesviathe dipole-dipole mechanism[24],this factor was assigned to and determined as the spectral overlap between the absorption band of the acceptor and the emission band of the donor.As a result,the emission spectrum of the donor and the absorption spectrum of the acceptor are recorded separately and properly rescaled to determine the area under which these spectra overlap.However,this requires the spectra of the isolated donor and acceptor,which might not be viable,as well as a delicate procedure for determining the area of the spectral overlap.This would also preclude the development of a quantitative and predictive model.Considering that the density of statesρD(E)andρA(E)are Gaussian functions,then the area of their overlap can be expressed as a sum of two error functions that depend on the widths of the Gaussian functions,their energy maxima,and the point of their intersection.Despite this area being calculable,there is not an analytical expression for it,which requires numerical modeling.

It should be noticed that a typo occurred in the expression ofWmd-mdin previous publications[16,37,56],wherewas used instead ofas shown in Eq.（20）.Indeed,because the electric dipole interactions,which are shielded by electron densities represented as,have different nature than the magnetic dipole interactions,the shielding of these interactions,represented as,should not be the same.Hence,the introduction of the new notation.However,because the shielding of the 4f electrons by the remaining electrons of the lanthanide ion and of the ligands involves closed-shells（e.g.,5s25p6）,then it is expected that the magnetic shieldingshould be very small.This reasoning,associated with the difficulties in modelinghas prompted the complete neglect ofin the equation forWmd-md[57-58]or to considerin the calculations ofWmd-md[16,37,56],which will cause a slight overestimation of theWmd-mdrate.

During the study of the plasmon effects on the luminescence of lanthanide ions,an alternative model was developed to determine the contributions of the density of statesρD(E)andρA(E)to theF-factor[59].Later,the overlaps of the vibrational states were taken into consideration to develop a more complete formulation of theF-factor,which becomes a function of the temperature by assuming a Boltzmann distribution for the vibrational states of the initial and final electronic states[20,34].This formulation is relevant because it explicitly accounts for the creation of phonons when the donor state has energy higher than the acceptor.It also accounts for the annihilation of phonons when the donor state is below in energy relative to the acceptor state because the energy mismatch must be compensated by phonons[20].By considering the bands of the donor and acceptor,ρD(E)andρA(E'),have Gaussian profiles,an analytical expression for the integral of a product of two Gaussian functions can be obtained[60].This comes from the fact that a product of two Gaussian functions is a well-defined Gaussian function,whose define integral has analytical expression and theF-factor can be expressed approximately as（in erg-1）[34]

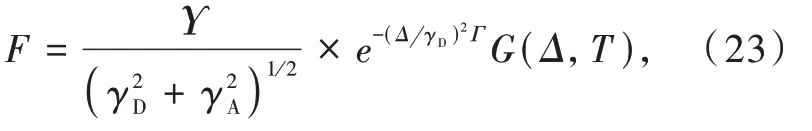
where

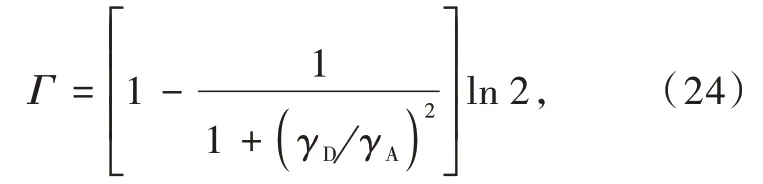
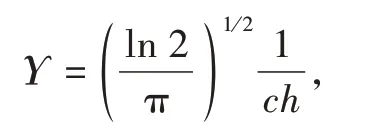
withγDandγAbeing the bandwidths at half-height（in cm-1）of the donor and acceptor,respectively,so 2πcћγxhas units of energy（in erg）,Δ（in cm-1）being the energy difference（mismatch）between the donor and acceptor states,Δ=ED-EA,andΥ=2.3646184×1015cm-1·erg-1.The functionG(Δ,T)in Eq.（23）collects contributions from the overlaps of the vibrational wavefunctions,which can be expressed in terms of the Huang-Rhys parameters with dependence on the average vibrational quantum number and on the number of phonons required for energy conservation.An approximated expression for this function is

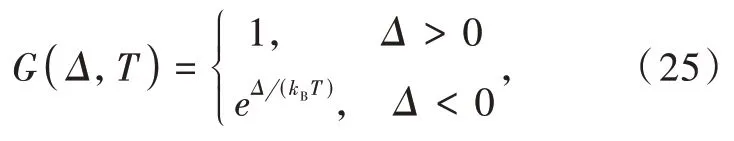
which represents an approximation to the multiphonon mechanism used to compensate for the energy conservation,withkBbeing the Boltzmann constant.

This reorganized form of theF-factor shows explicitly its dependence on the energy mismatchΔand the bandwidthsћγDandћγA.For instance,in the case ofLn-Lnenergy transfer,the bandwidths are narrow and practically the same,γD≅γA≡γ,soF=For narrow bands,the restriction on the energy mismatchΔis quite severe.For instance,γ≅200 cm-1givesF≅8×1012e-0.35(Δγ)2erg-1,forΔ＞0.IfΔ≅1 000 cm-1=5γ,thene-0.3466·52～10-4andF～109erg-1;however,ifΔ≅2 000 cm-1=10γ,thene-0.3466·102～10-15andF～10-2erg-1.So,a twofold increase inΔleads to a 1011decrease ofF,because of the quadratic dependence onΔin the argument of the exponential.This situation is quite distinct from that involving a sensitizer with a broad band,whereγD≫γA.In this case,theF-factor becomes.So,for a donor bandwidth ofγD≅2 000 cm-1andΔ≅6 000 cm-1=3γD,thenF～2×109erg-1.Despite this energy mismatchΔbeing six times larger than that of narrow bands,theF-factor is the same order of magnitude because it corresponds to three times the broader bandwidth,whereas in the latter case it corresponds to five times the narrower bandwidth.

The dependence of theF-factor on the energy mismatch,bandwidths,and temperature is depicted in the following Figs.

Fig.1 shows that theF-factor is slightly asymmetric because the functionG(Δ,T)differs whenΔ＜0 orΔ＞0（Eq.25）.For very narrow bandwidths values（e.g.,γD=γA≈100 cm-1）,theF-factor assumes high values only ifΔis in the same order as bandwidths.

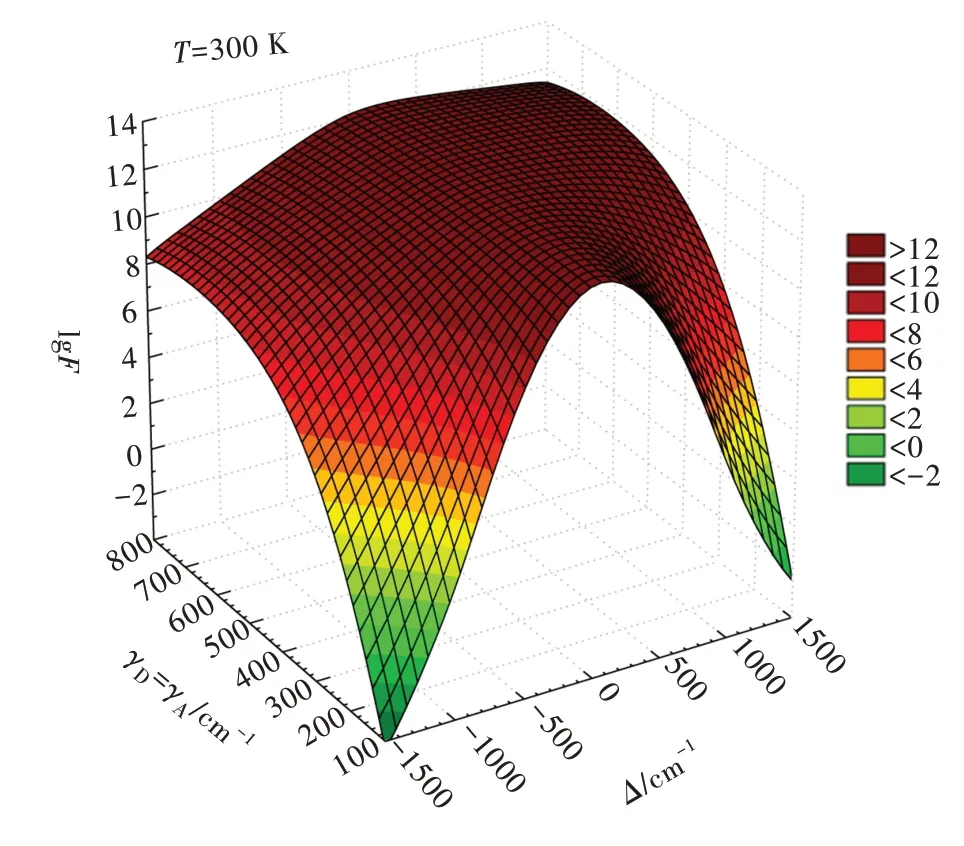
Fig.1 Dependence of the F-factor on the energy mismatchΔ and the bandwidthγ，forγD=γA=γand temperature T=300 K.Graph in linear scale in Fig.S1.

Temperature effects on the energy transfer rates can be rationalized from the changes of theF-factor.Thus,two outcomes（direct and indirect）are expected:the energy mismatch barrier in theG(Δ,T)whenΔ＜0（direct）and the widening of the bandwidths due to the temperature rising（indirect）.Fig.2 shows theF-factor behaves as a function of temperature（direct）and ofΔ,for fixed values ofγD=γA≈400 cm-1.For the temperature effects on the bandwidth broadening,consider the following hypothetical case:a co-doped Nd（Ⅲ）,Yb（Ⅲ）-containing material at an initial temperatureTipresentsγD(Ti)=γA(Ti)≈300 cm-1for a pair of donor and acceptor transitions（e.g.,Nd（Ⅲ）4G5/2→4I15/2as donor and Yb（Ⅲ）2F7/2→2F5/2as acceptor,withΔ≅1 100 cm-1[47]）,and the sample is uniformly heated to a final temperatureTfand both bandwidths increase by 50 cm-1,so（γD(Tf)=γA(Tf)≈350 cm-1）.According to Eq.（23）and approximatingΔ≅1 000 cm-1（as illustrated in Fig.3）,theF-factor increases from 1.18×1011to 2.82×1011erg-1.

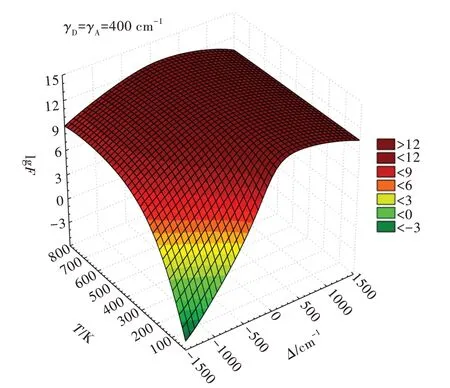
Fig.2 Dependence of the F-factor on the energy mismatchΔ and the temperature.γD=γA=400 cm-1.Graph in linear scale in Fig.S2.

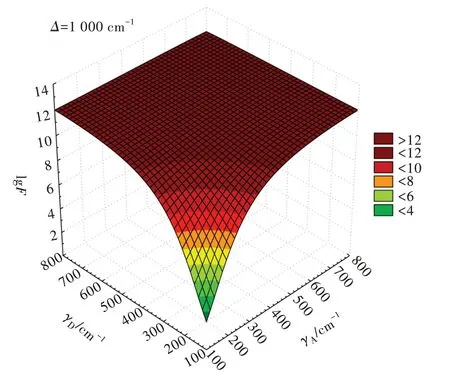
Fig.3 Dependence of the F-factor on the energy bandwidths of the donor（γD）and the acceptor（γA）.Δ=1 000 cm-1.Graph in linear scale in Fig.S3.

Notice that the graph in Fig.3 presents symmetry with respect to the interchange ofγDandγAvalues,which is not evident in Eqs.（23）and（24）because of thee-(ΔγD)2Γterm.However,it makes sense once the Dirac delta function acting inkandistates should be the same when the order of states is reversed,i.e.,δ(Ek-Ei)=δ(Ei-Ek)in Eq.（7）.

6 Selection Rules for Energy Transfer Rates

Lanthanide ions have a wealthy number of levels in the optical region that can be active in energy transfer processes.So,the number of ET pathways between two lanthanide ions can be substantially large and the selection rules are important to exclude those pathways that are null.In fact,the selection rules of theJquantum number,together with the energy mismatchΔ,in Eq.（23）,are very useful to select the donor and acceptor states for adequate ET pathways.

The exchange contribution,Eq.（17）,to the ET ratedoes not have selection rulesfor theJquantum number,that is,it always present,regardless of the donor or acceptor states.This is particular to lanthanide-lanthanide ET processes because in this case,the isotropic contribution does not vanish,so no dependence on the angular momentum appears.For the case of ligand-lanthanide ET processes,because the ligand states are usually restricted to singlets and triplets,with a singlet ground state,the contribution from the spin operator vanishes and only transitions with|ΔJ|=0 or 1 are allowed（nonvanishing）[20].Despite this lack of selection rules,the exchange contribution is strongly dependent on the lanthanidelanthanide distance,RDA,because ofin Eq.（17）,and,mainly ofdependence.Indeed,the overlap integral between 4f-4f radial functions,ρff,decreases rapidly with the lanthanide-lanthanide distance（Fig.4）[53].As a result,depending on the value of theF-factor,the exchange contribution,Wex,can be promptly ruled out and would be considered mostly when the other contributions are null.

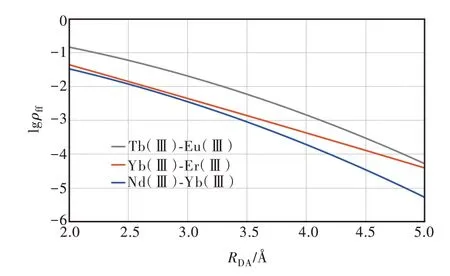
Fig.4 4f-4f overlap integrals（lg scale ofρff）as a function of Ln-Ln distance（RDA inÅ）for the Tb（Ⅲ）-Eu（Ⅲ），Yb（Ⅲ）-Er（Ⅲ），and Nd（Ⅲ）-Yb（Ⅲ）pairs.DFT calculations with BP86 functional［61-62］，TZ2P basis set［63］，and the inclusion of ZORA scalar relativistic effects［64-65］were performed in the ADF program［66］.Parametric functions derived from these calculations for any Ln-Ln pair can be found in reference［53］.Graph in linear scale in Fig.S4.

In the case of the multipolar mechanisms,Wd-d,Wdq-qd,andWq-q,the selection rules are:|J*-J|≤K≤J*+J.These come from the fact that these rates will vanish when the dipoleor quadruplestrengths are null.On the other hand,these quantities will be null when all reduced matrix elementsare zero,hence these selection rules.For instance,consider the5D4→7F5transition of Tb（Ⅲ）as a donor state,then|=1 and+JD=9,so 1≤K≤9 which covers all possible values ofKand increases the chance of having nonzero matrix elements.On the other hand,if the acceptor state is the7F0→5D1transition of Eu（Ⅲ）,then=1 and+JA=1,soK=1 and the transition is forbidden because matrix elementsare zero.However,these selection rules may be slightly relaxed by theJ-mixing effect,providing very small values of≈0.0032×0.052for the specific cases involving the Eu（Ⅲ）7F0level.Therefore,this effect is negligible in the energy transfer between lanthanide ions.

So,the contributions from multipolar mechanisms,Wd-d,Wdq-qd,andWq-q,to the ET rateviathe pathway Tb（Ⅲ）5D4→7F5to Eu（Ⅲ）7F0→5D1are null.However,this pathway is allowed by the exchange mechanism and might be allowed by the magnetic dipole mechanism.Hence,for the multipolar mechanisms,another acceptor state of Eu（Ⅲ）needs to be considered,e.g.,7F1→5D1.In this case,=0 and+JA=2,soK=2 and the7F1→5D1transition is allowed because matrix elementU()2of Eu（Ⅲ）is nonzero.

The remaining mechanism for ET between lanthanide ions is the magnetic dipole-magnetic dipole,Wmd-md,in Eq.（16）and（20）.Thus,the selection rules are given by thematrix elements,which will be zero unlessΔJ=0,±1,exceptJ*=J=0.As a result,theWmd-mdcontribution to the ET rateviathe Tb（Ⅲ）5D4→7F5to Eu（Ⅲ）7F0→5D1pathway will be nonzero becauseΔJ=±1 for both transitions,which satisfy the selection rules.

Notice that for Eu（Ⅲ）,the first excited state7F1is close to ground level7F0,so the populations of these states will depend on the temperatureviathe Boltzmann factor.When comparing the relative contributions of each mechanism to the total ET rate,it is common to weigh those rates involving the7F0and7F1levels by ca.0.65 and 0.33（at 300 K）,respectively.However,care must be exercised when the ET rates are going to be employed in the rate equations.In this case,the thermal effects are already included in the initial populations when solving the rate equations,so the weighting procedure should not be overcounted.

7 Forced Electric Dipole Intensity Parameter，ΩK（FED）

The forced electric dipole（FED）contribution to the intensity parameterΩK（withK=2,4,and 6）,that appears in the（forced）electric dipole strengthSd,Eq.（18）,is perhaps one of the most difficult quantities to determine.It cannot be determined from fitted values of experimental absorption or emission spectra,because the fitted intensity parametersΩKcontains contributions from both FED and dynamic coupling（DC）mechanisms.Usually,the FED contribution toΩKis very small;however,it depends on the lanthanide ion and its environment,so no trends have been observed[37,67-69].It cannot be neglected,because despite it being small,the contributions of theWd-dandWdq-qdrates can be relevant or even dominant for several ET pathways.In addition,ΩK(FED)contains effects from the environment of the lanthanide ion,which can be used to design systems with more efficient ET pathways.Therefore,values ofΩK(FED)have to be obtained from quantitative models.For instance,the simple overlap model（SOM）[55,70]yields quantitative expressions forΩK(FED),which can be evaluated using the JOYSpectra web platform[71].For Eu（Ⅲ）and Tb（Ⅲ）in a unique ninecoordination site of the doped material Sr3Tb0.90Eu0.10-（PO4）3[36,71],two sets ofΩK(FED){Ω2;Ω4;Ω6}（in units of 10-20cm2）are obtained:{0.60;0.21;0.26}for Tb（Ⅲ）and{0.82;0.38;0.52}for Eu（Ⅲ）.

These calculations were performed using the values of the force constant,kLn-L,of theLn-Ligating atom bond obtained from density functional theory（DFT）calculations and,therefore,the values of theg-charge factors were determined for allLn-O pairs with Eq.S80[36].In the specific case of Sr3Tb0.90Eu0.10-（PO4）3materials,the calculatedkLn-Lis in the range of 0.38-0.42 mdyn/Åand it providesg-charge factors around 1.29.For further details on applying the SOM model,see Supporting Information and references[20,35,55,67,70-76].

8 Illustrative Examples of How to Calculate Energy Transfer Rates

Here we will illustrate step-by-step examples of some energy transfer pathways betweenLn（Ⅲ）ions.The first example（E1）involves the Tb（Ⅲ）[5D4→7F5]→Eu（Ⅲ）[7F1→5D1]energy transfer pathway which is the dominant one for Tb-Eu processes[36-37].As an exercise of a direct application of selection rules onJ,the Tb（Ⅲ）[5D4→7F5]→Eu（Ⅲ）[7F0→5D1]（E2）will also be addressed.These two pathways are illustrated in Fig.5.

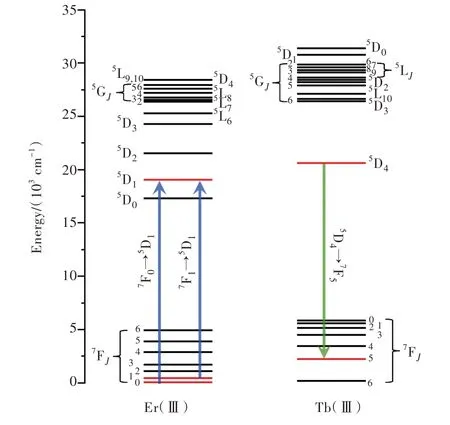
Fig.5 Energy level diagram showing Eu（Ⅲ）and Tb（Ⅲ）levels.The green arrow denotes the Tb（Ⅲ）5D4→7F5 transition（donor）while the blue lines represent Eu（Ⅲ）7F1，0→5D1 transitions（acceptors）.The levels involved in E1 and E2 are highlighted in red.

Since the discovery of the upconversion process by F.Auzel[77-78],ET between lanthanide ions has become an important issue regarding luminescent materials based onLn（Ⅲ）ions[79-84].Thus,we will also show how to calculate two energy transfer steps that are in good energy resonance conditions:Yb（Ⅲ）[2F52→2F72]→Er（Ⅲ）[4I152→4I112]（E3）and Yb（Ⅲ）[2F52→2F72]→Er（Ⅲ）[4I112→4I72]（E4）pathways[16,35].Fig.6 illustrates these pathways in E3 and E4.

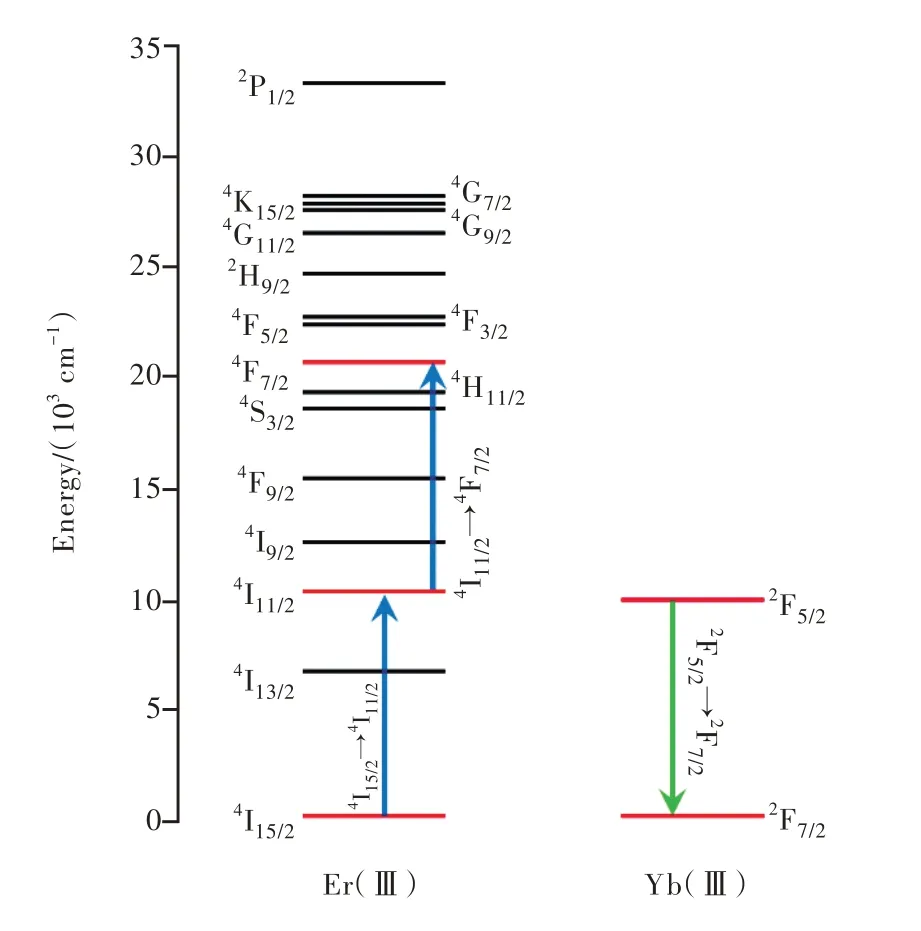
Fig.6 Energy level diagram showing Er（Ⅲ）and Yb（Ⅲ）levels.The green arrow denotes the Yb（Ⅲ）2F5/2→2F7/2 transition（donor）while the blue lines represent the two upconverting transitions（acceptors）considered in E3 and E4.All levels involved in the energy transfer examples are highlighted in red.

·E1

Tab.1 contains the input data considering Tb（Ⅲ）[5D4→7F5]and Eu（Ⅲ）[7F1→5D1]transitions as donor and acceptor,respectively.

Thus,when the data in Tab.1 is applied to the indicated equations with the sets ofΩK(FED),mentioned previously for the case of Sr3Tb0.90Eu0.1（0PO）43[36],we obtain the following rates for each mechanism:

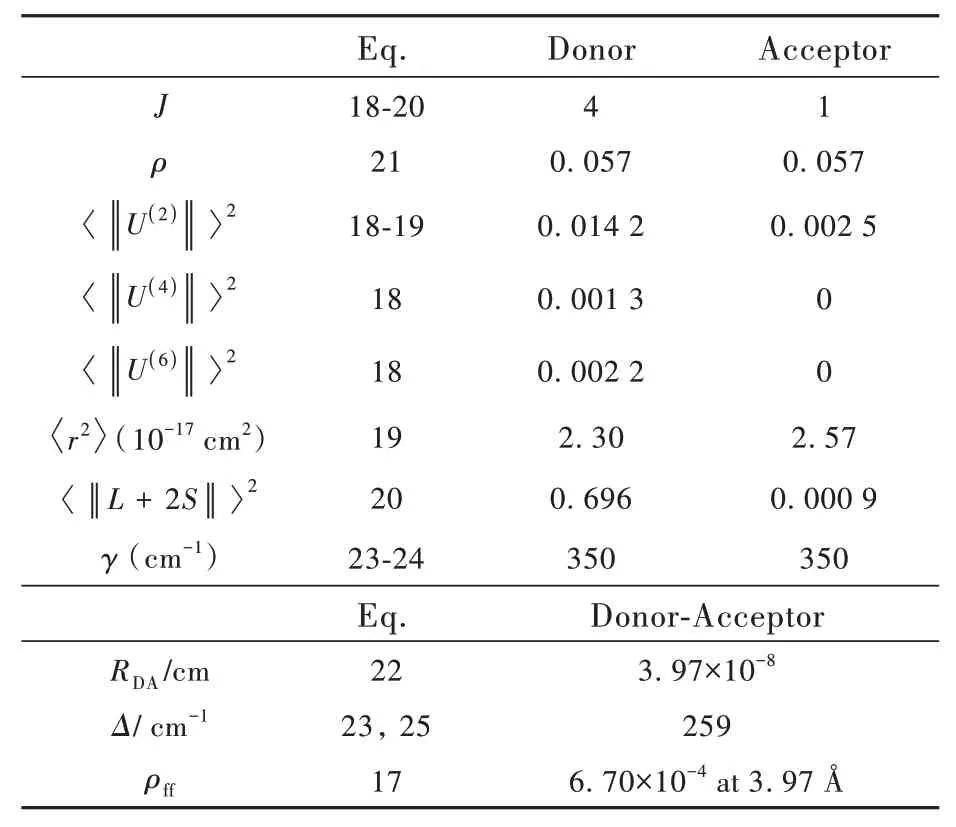
Tab.1 Input data used to calculate the Tb（Ⅲ）［5D4→7F5］Eu（Ⅲ）［7F1→5D1］in E1.The number of the equation where the input data enters is also indicated

The total energy transfer rate is given by the sum of all these contributions and multiplied,in this case,by the7F1population fraction（ca.0.33 at room temperature）:

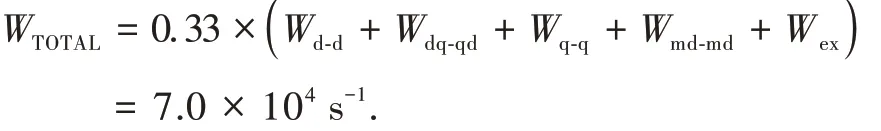
These rates are in agreement with those presented in reference[36]for the same pathway at the sameRDAdistance.A slight deviation in the quadrupolequadrupole mechanism from reference[36]（Wq-q=5.67×104s-1）was observed.This is due to the use ofr2=2.57×10-17for the Tb（Ⅲ）.

·E2

To estimate each contribution to the rate of the Tb（Ⅲ）[5D4→7F5]→Eu（Ⅲ）[7F0→5D1]pathway,some values in Tab.1 need to be updated to match the7F0→5D1transition（Tab.2）.

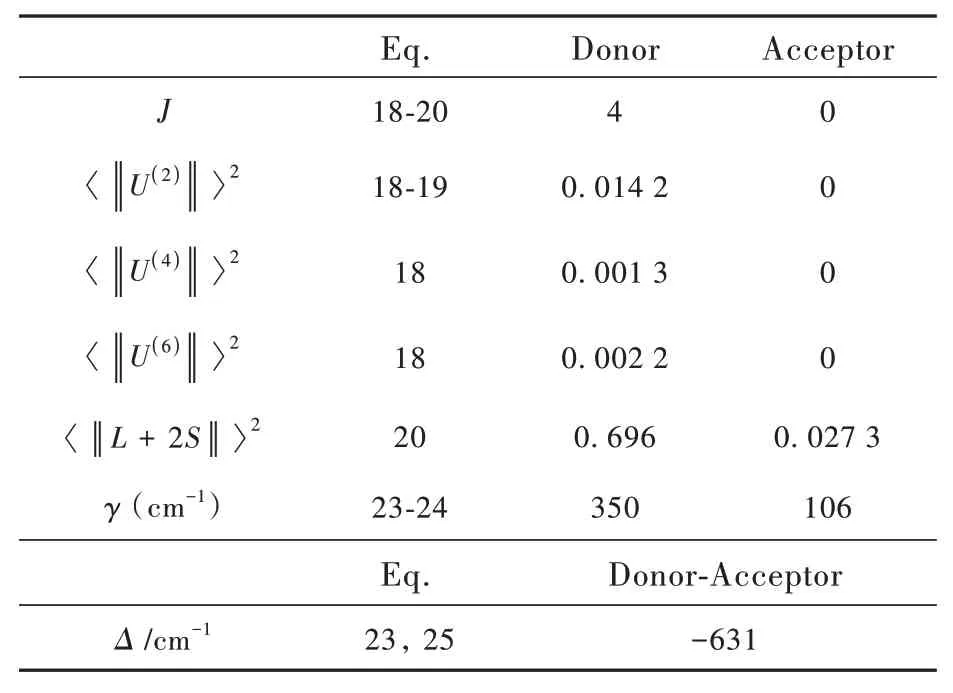
Tab.2 Input data used to calculate the Tb（Ⅲ）［5D4→7F5］→Eu（Ⅲ）［7F0→5D1］in E2.The number of the equation where the input data enters is also indicated.The other quantities that are not displayed are still the same as presented in Tab.1

It can be noticed that for this pathway,according to the selection rules,the7F0→5D1transition has all=0.Therefore,Wd-d=Wdq-qd=Wq-q=0 and this pathway has only the contributions of theWex=3.3×103s-1andWmd-md=1.3×101s-1,in accordance with those in reference[36].Adding these rates,considering the7F0population fraction（ca.0.64 at room temperature）,and the energy barrier factorG(Δ,T),yields the total rate:

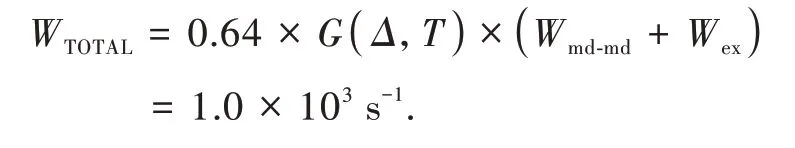
It is important to pay attention that,in this case,G(Δ,T)was considered outside of theF-factor just to match with the data in the literature.But it must be considered for each case appropriately.

·E3

The first step in the Yb-Er upconversion process is given by the Yb（Ⅲ）[2F5/2→2F7/2]→Er（Ⅲ）[4I152→4I112]pathway.Tab.3 contains the data for calculating the pairwise energy transfer for the shorter Yb-Er distance（RDA=3.5Å）in NaYF4∶Yb,Er material.

Applying the data in Tab.3 leads to:

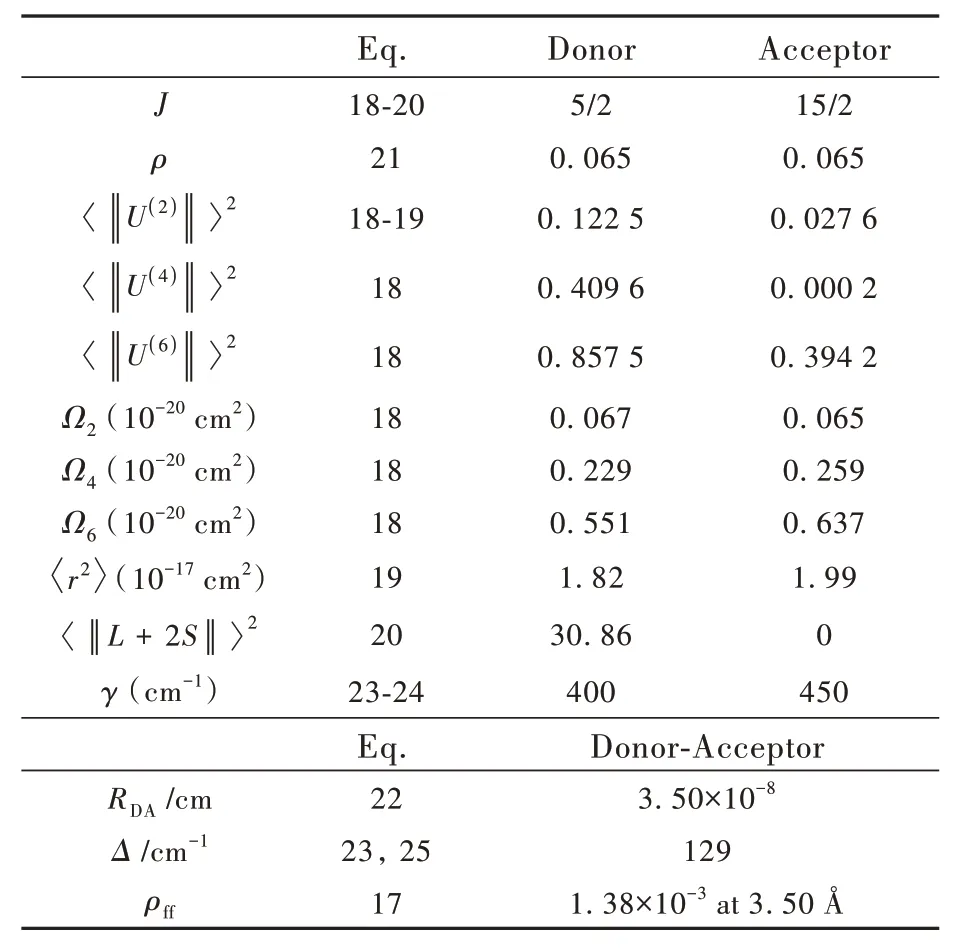
Tab.3 Input data used to calculate Yb（Ⅲ）［2F5/2→2F7/2］→Er（Ⅲ）［4I15/2→4I11/2］in E3.The number of the equation where the input data enters is also indicated.The values ofΩK represent those obtained only with the FED contribution

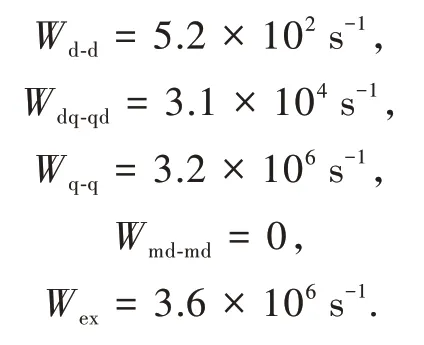
The total pairwise energy transfer Yb（Ⅲ）[2F52→2F72]→Er（Ⅲ）[4I152→4I112]pathway isWTOTAL=6.9×106s-1,which also reproduces the value for the shortest Yb-Er distance for the first upconverting step from reference[16].

·E4

Repeating the same procedure as E3 but updating the acceptor transition from4I152→4I112to4I112→4I72,we obtain the input data in Tab.4.

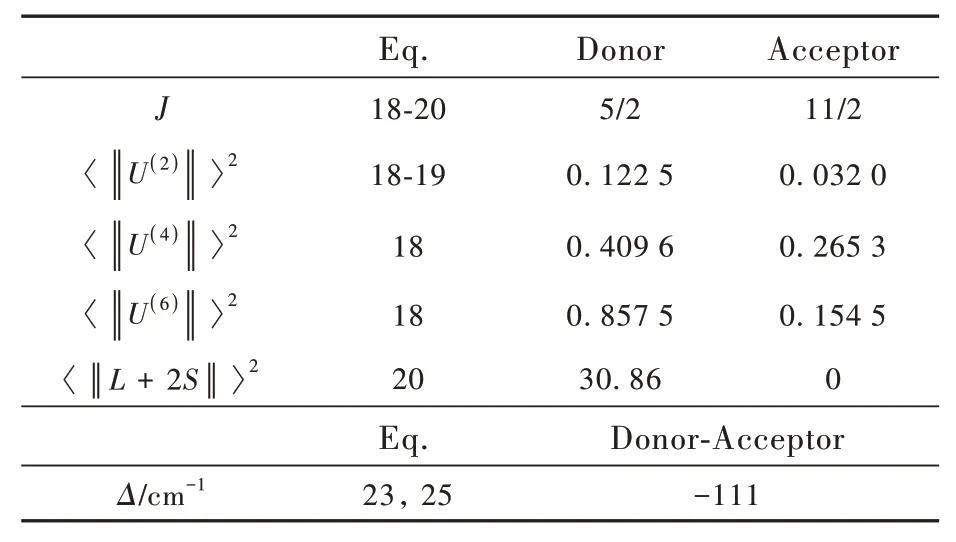
Tab.4 Input data used to calculate the Yb（Ⅲ）［2F5/2→2F7/2］→Er（Ⅲ）［4I11/2→4I7/2］in E4.The number of the equation where the input data enters is also indicated

In this case,the total pairwise energy transfer of the Yb（Ⅲ）[2F52→2F72]→Er（Ⅲ）[4I112→4I72]pathway isWTOTAL=5.1×106s-1,in agreement with the value for the shortest Yb-Er distance for the second upconverting step from reference[16].

All these examples are worked out as separated Mathcad® script files available in the Supporting Information（Examples_Mathcad.zip）.

9 Conclusions

In this tutorial review,we presented the equations for the energy transfer rates between lanthanide ions in an alternative form,which aimed at an easier interpretation and a simpler step-by-step calculation.Four examples were provided to illustrate this procedure for relevant lanthanide pairs.We expect that the present work will guide students and stimulate the research fn the field of energy transfer between lanthanide ions.

Acknowledgments

The authors are grateful for the financial support from CNPq,CAPES,FACEPE,and FINEP agencies.This work was funded by the Public Call n.03 Produtividade em Pesquisa PROPESQ/PRPG/UFPB project number PVN13305-2020,and PROPESQ/CNPq/UFPB PIN11132-2019.This work was developed within the scope of the project CICECO-Aveiro Institute of Materials,UIDB/50011/2020 and UIDP/50011/2020,financed by Portuguese funds through the FCT/MEC and when appropriate co-financed by FEDER under the PT2020 Partnership Agreement.RLL is grateful for the partial financial support under grants:Pronex APQ-0675-1.06/14,INCT-NANOMARCS APQ-0549-1.06/17,APQ-1007-1.06/15,and CNPq-PQ fellowship(Proc.309177/2018-9).

Author Statement

Albano N.Carneiro Neto:Conceptualization,Methodology,Software,Validation,Formal analysis,Investigation,Data Curation,Writing-Original Draft,Writing-Review & Editing.Renaldo T.Moura Jr.:Conceptualization,Writing-Review & Editing.Jorge A.A.Coelho:Conceptualization,Methodology,Writing-Review & Editing.Mauro E.Silva-Junior:Conceptualization,Writing-Review & Editing.Janderson L.Costa:Conceptualization,Writing-Review & Editing.Oscar L.Malta:Conceptualization,Methodology,Formal analysis,Writing-Original Draft,Writing-Review & Editing,Supervision.Ricardo L.Longo:Conceptualization,Methodology,Investigation,Formal analysis,Writing-Original Draft,Writing-Review & Editing,Validation,Supervision,Project administration.

Supplementary Information and Response Letter are available for this paper at:http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.EN20220007.