基于Multisim和Matlab的一阶系统调节时间仿真

(广州南洋理工职业学院 信息工程学院，广东广州市，510900)黄勇超 邓发云

在经典的自动控制理论中，一阶系统的过渡过程没有超调部分，只有一个基于时间常数T的性能指标即调节时间，取5%误差带时的调节时间ts=3T。调节时间与时间常数的3倍关系，可用Matlab和Multisim仿真来分析。

MATLAB软件由开发环境、数学函数库、编程语言、图形处理系统和应用程序接口等部分构成，内含图形化用户界面、大量的计算算法以及调用C、Fortran程序。MATLAB软件具有强大的数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真功能。Matlab编程及其内含的Simulink仿真可以让学生直观认识一阶系统调节时间与时间常数的关系。

一阶系统通常由一阶RC电路实现，因此，一阶系统的过渡过程也可用Multisim仿真来分析。

Multisim软件有丰富的数据元件、强大测试仪器、完备的电路分析手段[1]，可以解决理论教学与实际动手的脱节[2]，其中的实际元器件使设计仿真与实际情况有良好的对应性，可以直接导出到Ultiboard中进行PCB的设计，其中的虚拟元器件只能用于仿真，可以根据需要改变的参数值[3]。Multisim仿真搭建一阶RC电路，可以逼真再现实验环境，直接分析电路的内部和外部特性[4]，同样可以验证一阶系统调节时间与时间常数的关系。

下面以一阶RC电路为例分析一阶系统调节时间与时间常数的关系。

1 一阶RC电路的理论调节时间

图1所示的一阶RC电路中，输入电压Ur时电流立即对电容C充电，最后电压Uc=Ur进入稳定状态，结束充电的过渡过程。

图1 一阶RC电路

该一阶RC电路微分方程可推导求得：

图1中，设一阶RC电路的R=100KΩ，C=1uF，初始条件为y(0)=0以及y′(0)=0，则电路的时间常数T=RC=0.1s。

将(1)式进行拉氏变换，可得一阶RC电路的传递函数为：

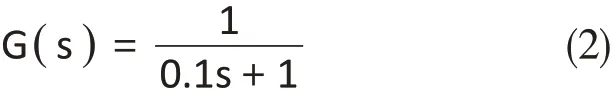
令输入电压Ur=10V，在零初始状态下，一阶RC电路的阶跃响应为：对(3)式进行拉氏反变换，可以得到：

在(4)式中，uc对时间t单调递增。按5%的误差计算一阶RC电路的调节时间，令Uc(t)=9.5，可得t=0.3，即电路的理论调节时间ts=3T=0.3s。

2 一阶RC电路的Matlab仿真

在Matlab软件中，一阶RC电路的调节时间可以通过结合5%的误差带求解(1)式求得。在Matlab开发环境中输入以下的程序段解微分方程，可以计算一阶RC电路在5%的误差带下的调节时间ts。

plot(t，uc，t，uc1)%以t为横坐标，绘制输出电压Uc及其下限值uc1曲线

运行以上程序，可得一阶RC电路的调节时间ts=0.3s，与理论调节时间相同。

运行以上程序还可得到如图2所示的一阶RC电路的响应曲线，游标显示出95%的输出电压与响应曲线交点(0.3，9.5)，即运行时间大于0.3s时，一阶RC电路的输出电压进入5%的误差带。

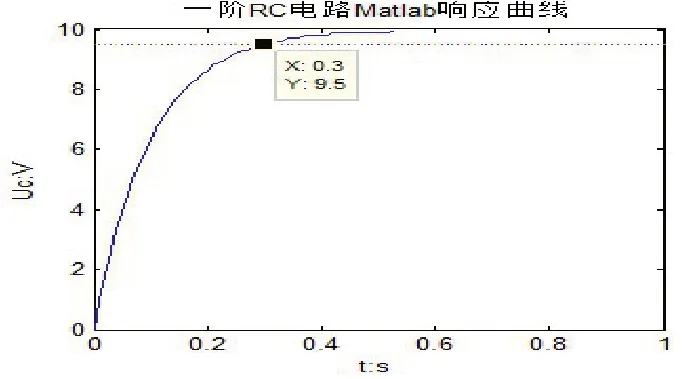
图2 一阶RC电路响应曲线

3 一阶RC电路的Simulink仿真

根据一阶RC电路的传递函数(3)式，在Matlab软件中搭建如图3所示的一阶RC电路的Simulink仿真系统，输入电压为Ur=10V可用单位阶跃信号增益k=10代替。图3中，仿真系统含有一阶RC电路仿真和95%阶跃输入信号两个前向通道，虚拟示波器scope模块显示两个通道的响应曲线。

图3 电路的SIMULINK仿真系统

运行SIMULINK仿真系统，输出scope模块以后，在命令窗口输入如下函数：

两个set函数调出Scope模块的编辑栏，通过编辑栏对scope图形的标题栏、横轴、纵轴、两个通道的交点进行编辑，得到一阶RC电路的Simulink仿真结果及5%的误差带如图4所示。

从图4中的游标可以看出，95%阶跃信号与响应曲线的交点对应的调节时间为0.3s左右，与Matlab编程得到的结果一致。

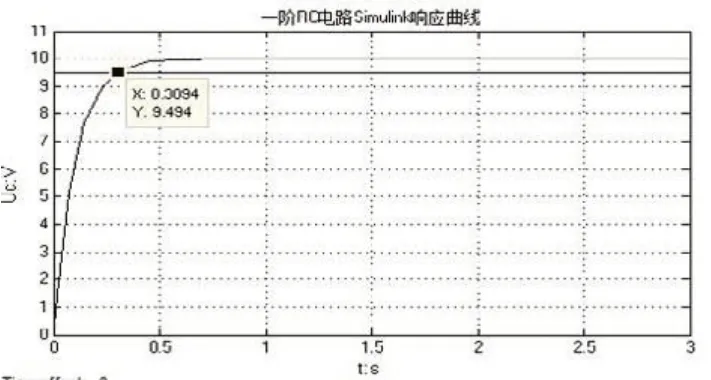
图4 一阶RC电路的Simulink仿真结果及5%的误差带

4 一阶RC电路的Multisim仿真

根据图1所示的一阶RC电路图，在Multisim中搭建如图5所示的一阶硬件电路模拟电路，并用虚拟示波器XSC观察输出电压Uc的变化。

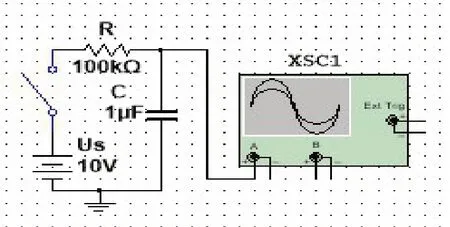
图5 一阶硬件电路模拟电路

对图5所示的一阶RC电路进行Multisim仿真。点击虚拟示波器XSC弹出示波器图形界面，然后合上电路开关，随着时间变化，实时得到一阶RC电路的Multisim响应曲线如图6所示。图6中反映出时间从0时刻开始的电容C上得到的充电电压与充电时间的关系，再现了电容C真实的充电过程。

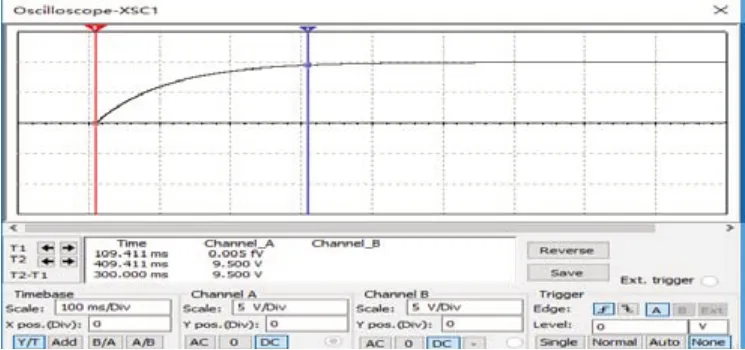
图6 一阶RC电路的Multisim响应曲线

在虚拟示波器XSC的图形界面中，移动1号游标到响应曲线的起点(0V)找到运行时间T1，移动2号游标到响应曲线上的9.5V(5%误差带的输出电压Uc下限值)找到运行时间T2，于是可以得到一阶RC电路的调节时间ts=T2-T1=0.3s。

图6可以看出，Multisim仿真得到的调节时间和理论调节时间是相同的，也和Matlab编程及Simulink仿真得到的结果一致。通过Multisim仿真，一阶RC电路的调节时间不仅可用Multisim的虚拟示波器XSC得到，还能看到完整的充电过程，而Matlab编程及Simulink仿真只能看到结果，这是Multisim的优势。

5 结论

本文一阶系统具体化为一阶RC电路，得到一阶RC电路系统。然后用10v阶跃电压作输入信号，简单推导了一阶RC电路的调节时间。采用Matlab微分方程编程、simulink传递函数仿真以及Multisim硬件模拟电路分析，对电路调节时间进行了图形分析，实时绘制出了响应曲线，调节时间都与理论值相同。

Matlab微分方程编程和simulink传递函数仿真得到的是仿真结果，Multisim电路仿真不仅能看到仿真结果，更主要地是能够看到电路工作过程。Multisim软件很方便地把电路工作过程真实地再现出来，在教学过程中做到变被动学习为主动学习，可用虚拟仪器技术开发，深得学生欢迎。