基于多特征的网络安全态势要素筛选方法研究

刘志明

（长沙民政职业技术学院 湖南 长沙 410004）

0 引言

在网络安全态势感知中，态势要素提取是首要步骤，主要是在收集到的多元异构数据中提取出会对态势环境造成影响的关键因素，这一步骤中提取的精准度会直接影响后续数据的处理与分析结果。但纵观目前常见的几种网络安全态势感知方法[1-3]，效果并不尽如人意。寇广等[4]提出基于反向传播算法和深度堆栈编码器的网络安全态势要素识别模型，并结合无监督学习算法实现对网络的训练。李腾飞等[5]提出基于拓扑漏洞分析的网络安全态势感知模型，借助有限状态机获取网络状态，并对其态势组成值进行计算，通过对态势要素的提取经过数值对比得出实际的网络安全状态。虽然上述两种方法都具有一定优势，效能较高，但在分类正确率和召回率方面却存在明显的不足之处。

为解决上述问题，本文提出基于贝叶斯卷积神经网络的网络安全态势要素提取方法，并采用非负矩阵分解算法进行多特征降维，获取到更为精准的态势要素信息分类函数，以此实现对特征空间的缩小，为后续的数据处理与分析提供便利。

1 基于贝叶斯卷积网络的态势要素提取模型

1.1 贝叶斯卷积网络

贝叶斯卷积网络（BCNN）是建立在概率分布基础上的一种神经网络模型[6-8]。通过在特定分布下对参数进行取值，每经过一次迭代计算，随机选取一个参数值进行特征运算，如图1所示为BCNN 的权重。

图1 BCNN 权重

BCNN 的权重参数并非是一个确定的值，而是服从一定概率分布下的一个随机变量，图2中的权重则是μ/σ。BCNN 能够借助对简单分布的构建逼近复杂拟合函数，结合概率模型和神经网络，实现对整个模型性能的提升。

1.2 基于BCNN 的态势提取

搭建BCNN 网络安全态势信息提取模型，如图2所示。

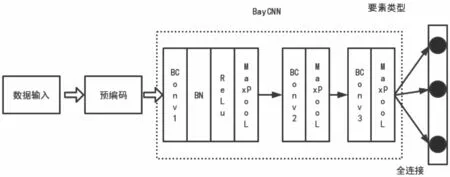
图2 BCNN 网络安全态势信息提取模型

BCNN 网络安全态势提取模型的卷积操作步骤如下：

第一，利用重参数化技巧在卷积核的权重分布中确定一个权重值，公式如下：

其中，convmean代表权重分布的均值，convstd代表权重分布的标准差，而∈～N（0,1）。

第二，利用感受野对获取到的卷积核进行卷积操作，公式如下：

其中，R代表感受野区域。

第三，利用重参数化对卷积层进行优化，将前向传播转变为可导，并在反向传播中更新权重高斯分布的参数，也就是均值和方差。

而在BCNN 网络安全态势提取模型的全连接层中，同样采用重参数方法进行参数采样。假设基于标准高斯分布进行采样，每个权重参数函数如下：

式（3）中，σ代表标准差，μ代表期望。

基于此可得到参数更新公式如下：

通过局部重参数化能够使变分情况下贝叶斯推断随机梯度的方差在后验概率模型参数中有所减少，并且具有可并行性。

2 态势要素多特征降维及构造分类器

2.1 态势要素多特征降维

基于上述获取到的态势要素信息，利用非负矩阵分解算法进行进一步的筛选和降维。具体过程如下：

对分类态势信息进行模糊，设定有分类质心组成非负矩阵分解基矩阵的初始值，而分类数量则是非负矩阵的分解秩数。

假设历史态势要素的集合为V=[v1，v2，…，vn]，其中n代表集合中的样本数量，当经过k分类得到的集合为F=[F1，F2，…，Fk]，其中k代表分类数量。而Uij表示的是历史态势要素对模糊向量的隶属度，对应矩阵为应注意的是Uij符合为此，制定隶属度的更新函数用下式表示：

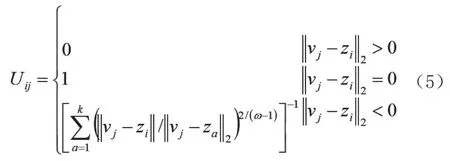
式（5）中，za代表初始聚类中心，zi代表第i个聚类中心，vj代表第j个历史态势要素，ω代表模糊加权指数。最终，确定聚类中心集合为：

目标函数为：

假如式（7）中的计算结果比阈值小，则停止迭代，同时对非负矩阵分解基矩阵W 的初始值进行设置，主要由聚类中心集合组成。

为此可分解历史态势要素矩阵Vm×n为Wm×n和Hm×n两个非负矩阵，二者相乘得到的积与原始非负矩阵无限逼近，Wm×nHm×n≈Vm×n。其中，Hm×n代表系数矩阵，Wm×n代表基矩阵，目标函数为最小化剩余Frobenius，用式（8）表示：

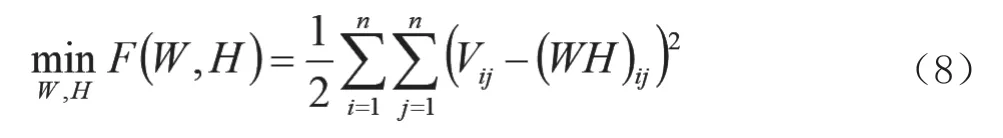
当V=WH时，取值是0。

收敛目标函数前，需利用模糊分类得到质心的初始化基矩阵，利用W和H矩阵间的交替更新，用下式代表矩阵的迭代规则：

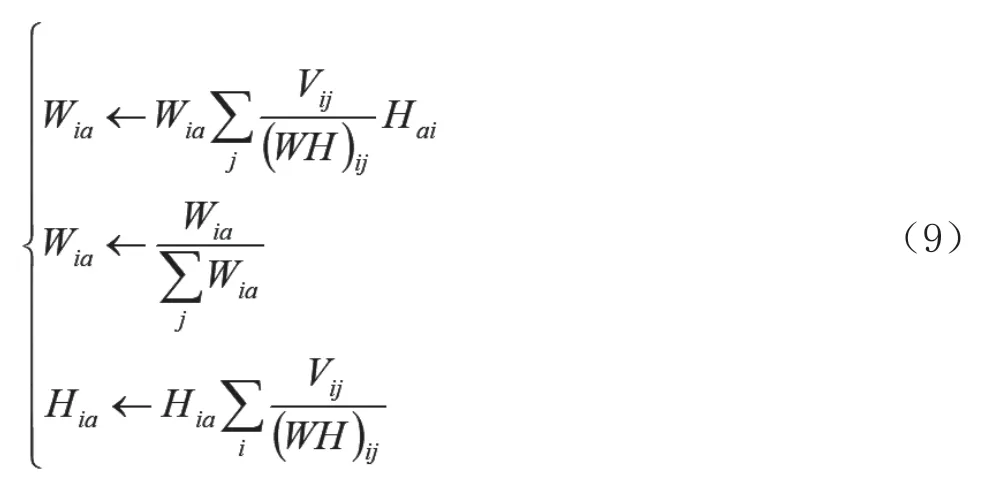
历经反复迭代，最终确定系数矩阵Hi和基矩阵Wi，并将之前的样本矩阵用系数矩阵替代，从而实现网络安全态势要素的多特征降维。

2.2 构造分类器

基于态势信息集合H=（xi，yi），用xi=（x1，x2，…，xj）表示集合中的某一元素，而代表类标签。针对任一类中的所有元素集合，在对应的高维空间内存在超球体（a，R）中含有所有的元素数量，对函数表达时进行优化，同时结合拉格朗日公式对其进行转化，转化后的表达式为

在上式中，L代表目标函数，而ai与aj代表拉格朗日因子。

利用d2（x）对集合中任一样本信息点与超球体球心间的距离进行表示，并借助高斯核函数对此距离进行计算，如下：

式（11）中，高斯核函数为k（xi，yj）。

由此可确定最终的分类函数为：

结合上式可对其分类展开训练，步骤如下：

步骤1：初始化超球体半径、球心为0，初始化拉格朗日因子为1/n，并计算训练样本信息点与超球体球心间的距离；

步骤2：在0 ＜ai＜C条件下，将满足此条件的样本点全部提取，并从中找出第一个与KFT 条件不符合的x1，执行步骤4；

步骤3：在ai=0，ai=C条件下，将满足此条件的样本点全部提取，并从中找出与KFT 条件不符合的所有样本点，当结果为0 时，执行步骤7；

步骤4：对条件max（｜d12-d22｜）进行设置，将x2确定为样本点，使目标函数为最大限度，并再次对拉格朗日因子进行优化，记为a1＇和a2＇；a2进行更新，之后再对得到的距离参数d12、d22和超球体

步骤5：依照上述得到的a1＇和a2＇，采用下式对半径参数R2进行更新；

步骤6：执行步骤2；

步骤7：训练结束。

3 实验结果与分析

3.1 实验数据及性能评价指标

实验数据选取NSL-KDD 数据集，包含正常与异常两种数据集。异常数据集中囊括R2L、DoS、U2R、Probe 四种常见攻击类型。数据分布情况如表1所示：

表1 数据分布

而性能评价指标的选择主要包括分类正确率、召回率及误警率。分类正确率为正确划分样本的数量与全部样本数量的比值；召回率为检测得到的正常类样本数量与全部样本数量的比值；而误警率为检测得到正常类样本中错误样本数量与全部样本数量的比值。运用这三个指标来实现对文中提出方法效果的检验。

3.2 实验结果与分析

运用SPSS 22.0 软件对确定的实验数据进行处理，分别以分类正确率、召回率和误警率为指标，对比文中提出方法和李腾飞等[5]提出的基于拓扑漏洞分析的要素识别方法，得到的结果如表2所示。

表2 文中提出方法和李腾飞等[5]提出方法实验结果对比

根据表2中的数据显示：对于分类正确率，基于拓扑漏洞分析的要素识别方法平均分类正确率为82.45%，而文中提出方法的平均正确率高达90.95%，可见文中提出方法的分类正确率相对较高；对于召回率，基于拓扑漏洞分析的要素识别方法的召回率，无论在何类别上均不计文中提出的方法；对于误警率，除DoS 类别外，文中提出方法的误警率均小于基于拓扑漏洞分析的要素识别方法。

4 结语

长期以来，网络安全态势要素提取都是网络安全领域的重点研究内容，为进一步提高网络安全态势要素提取的分类正确率、召回率，减少误警情况，提出基于BCNN 的网络安全态势要素提取方法，并在此基础上，利用非负矩阵分解算法实现多特征降维，构造分类器，最终实现对网络安全态势要素的进一步筛选。实验结果显示，所提出的网络安全态势要素提取方法分类正确率和召回率较高，误警率更低。