自适应前后向平滑算法在组合导航中的应用

何劢航，孙付平，肖 凯，车通宇，苗岳旺

自适应前后向平滑算法在组合导航中的应用

何劢航1，孙付平2，肖 凯2，车通宇1，苗岳旺1

（1. 61363部队，西安 710054；2. 信息工程大学，郑州 450001）

当全球卫星导航系统（GNSS）的导航信号受到部分遮挡或干扰，导致新息向量误差增大，会造成GNSS/INS（惯性导航系统）单向滤波误差增大，滤波误差将进一步干扰平滑效果，针对这一问题，提出一种自适应前后向平滑算法，算法在单向滤波时采用自适应卡尔曼滤波，通过自适应调节新息向量的方差协方差矩阵，减小误差的不利影响。一组跑车实验数据计算表明，自适应平滑算法精度要优于常规的平滑算法，可以有效减小误差。自适应前后向平滑算法三维位置误差的均值和标准差分别为25.03和8.94 cm，比未自适应处理精度分别提升21.66%和43.74%，对速度和姿态精度也有一定提升。提出的算法和实验结论可为组合导航数据后处理提供参考。

前后向平滑; 自适应滤波; 组合导航; 位置精度; 数据后处理

0 引言

在全球卫星导航系统（global navigation satellite system, GNSS）和惯性导航系统（inertial navigation system, INS）组合导航定位中，当卫星信号受到部分遮挡或者干扰时，可以依靠惯性导航提供短时的导航信息；但是随着遮挡干扰时间越长，误差增大。保证在GNSS观测质量不佳时依旧获得连续高精度的导航信息一直是组合导航的研究热点[1-2]。

常见的方法分为2种：1）神经网络训练和输出；2）平滑算法。文献[3-6]分别采用高斯回归过程、神经网络算法、支持向量机等多种模型作为训练方法，当GNSS信号良好时，对神经网络结构中的各类参数进行训练，当GNSS遮挡或失效时，以此作为输出进行量测更新，避免误差发散。但是载体当运动状态多变时，训练难度较大；因神经网络结构参数变化较大，输出结果不稳定[3-6]。平滑算法可以有效提高定位精度，主要包括前后向平滑（forward-backward-smoothing, FBS）算法和劳赫-通-斯特里贝尔（Rauch-Tung-Striebel, RTS）平滑算法。RTS平滑技术利用了相同历元间的动力学约束，可以有效提高速度和姿态的后处理精度[7-9]。而前后向平滑算法可以依靠前、后向滤波抵消部分误差影响。前后向平滑算法中，要进行2次独立的正向、反向滤波，传统的正向滤波是利用历史信息预测当前状态值，受当前观测值影响较大，逆向滤波的原理相同，一般采用正向滤波末尾历元信息作为起算依据[10]。文献[11]首次在国内提出了逆向惯性导航解算方法，但是没有给出误差方程[11]。文献[12]将前后向平滑算法应用于精密单点定位（precise point positioning, PPP）和INS紧组合后处理中，并且给出了详细的地心地固系的前后向误差方程，取得了良好的效果[12]。文献[13]结合FBS平滑和RTS平滑的优缺点，提出了一种二者融合的最优平滑算法[13]。前期的平滑算法研究中，主要采用常规的卡尔曼滤波技术，没有引入自适应算法来避免单向滤波误差发散的问题，并没有研究对比自适应滤波对前后向平滑的提升效果。

在平滑过程中，当GNSS信号受干扰或部分遮挡时，量测误差对前向或后向滤波都会带来影响，也必然会影响平滑的结果。所以本文提出一种自适应前后向平滑算法，在前向、后向滤波中都加入自适应滤波算法，以此减小观测量误差对滤波的影响。

1 组合导航滤波模型

1.1 前向滤波状态方程

本文采用当地地理系作为导航坐标系，状态方程依靠惯性导航误差方程进行构建。首先，前向惯性导航微分方程为

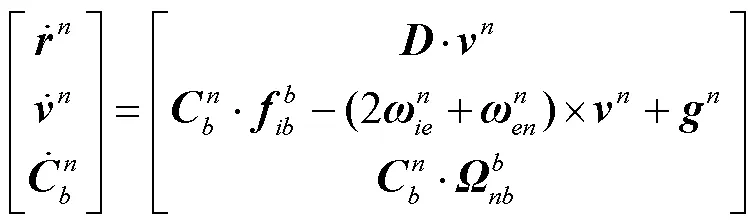
同理推导前向惯性导航误差方程，以前向微分方程为依据，构建前向滤波状态方程为

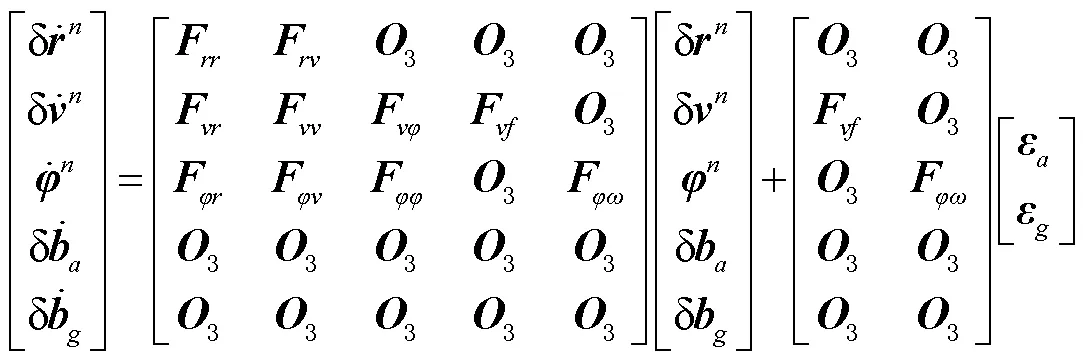
1.2 后向滤波状态方程

后向惯性导航微分方程是后向惯性导航解算和构建后向误差方程的基础，结构与前向微分方程相同，只须对若干参数取相反数，后向惯性导航微分方程为

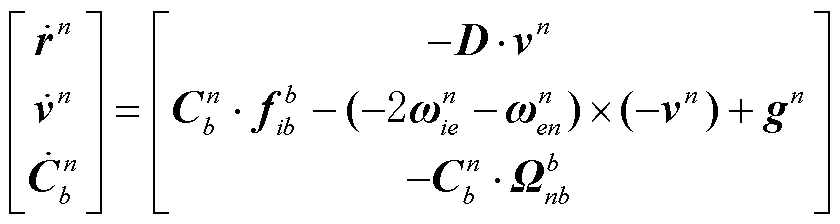
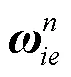
1.3 量测方程

本文采用位置速度为观测量的松组合模式，前后向滤波模型的量测方程一致，可以表示为

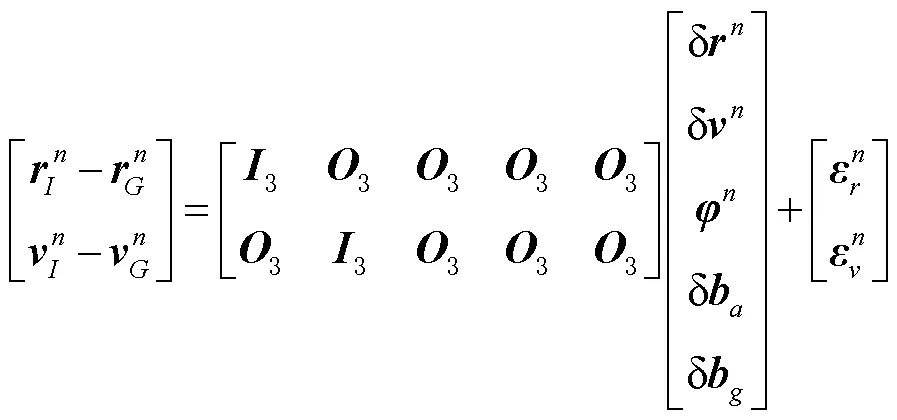
2 前后向自适应平滑算法

2.1 前后向平滑算法

前后向平滑算法主要分为3个步骤：

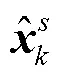
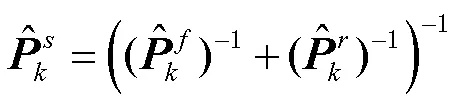
2.2 自适应滤波

在前、后向滤波中引入自适应算法，通过自适应算法调节观测噪声方差阵，以此减弱GNSS受部分遮挡或干扰时较大的粗差对定位结果的影响，即：

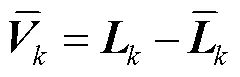
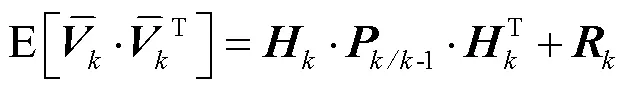
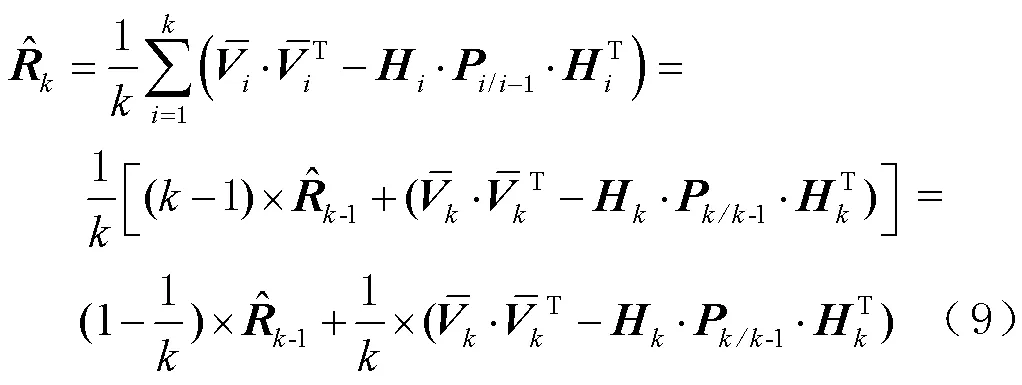
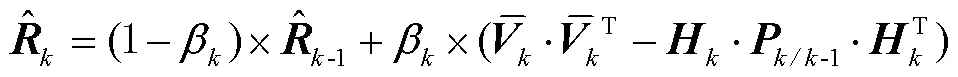
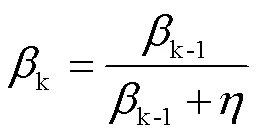
进一步对比自适应平滑和前向、后向以及前后向平滑。正向滤波时，当GNSS受到部分遮挡或干扰，导致组合的误差增大，当GNSS观测值恢复正常后误差重新收敛；逆向滤波同理。前后向平滑可以减小误差发散程度，自适应平滑算法通过在单向滤波中加入自适应算法，可在单向滤波中减弱GNSS误差影响，从而进一步提高平滑的精度。

3 实验与结果分析

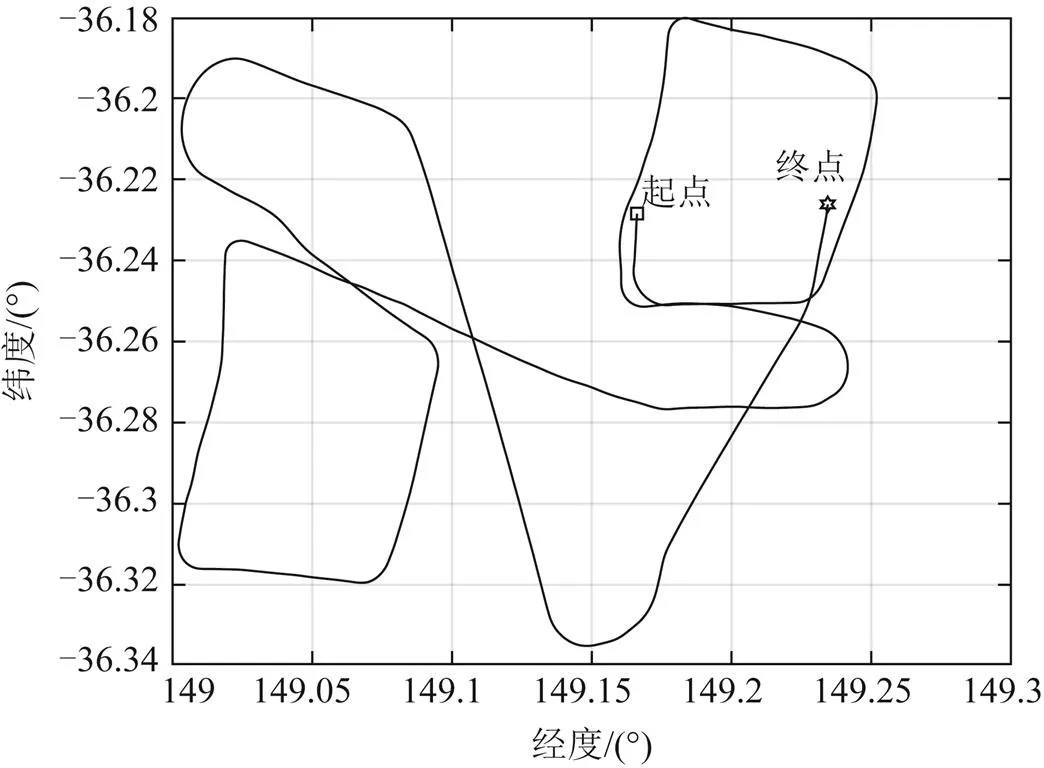
图1 实验跑车轨迹

3.1 位置误差平滑效果分析

令组合导航初始时刻为0，实验大约2.5 h，采样率为1 s，共计8000多个历元，对采用前8000个历元进行数据分析，在4000～4100 s的时刻段添加10 m的随机位置误差。主要目的是为了模拟GNSS观测值出现误差时对前后向滤波的影响，图2为4种滤波模式的位置误差。对比图2可以直观看出，使用自适应平滑算法后位置误差显著减小，加入10 m误差时间段内的前向、后向以及前后向平滑算法的位置误差受其影响导致误差增大，但是自适应平滑算法在单向滤波中已经通过自适应算法减弱了误差影响，所以平滑后误差没有增大，仍然保持良好精度。

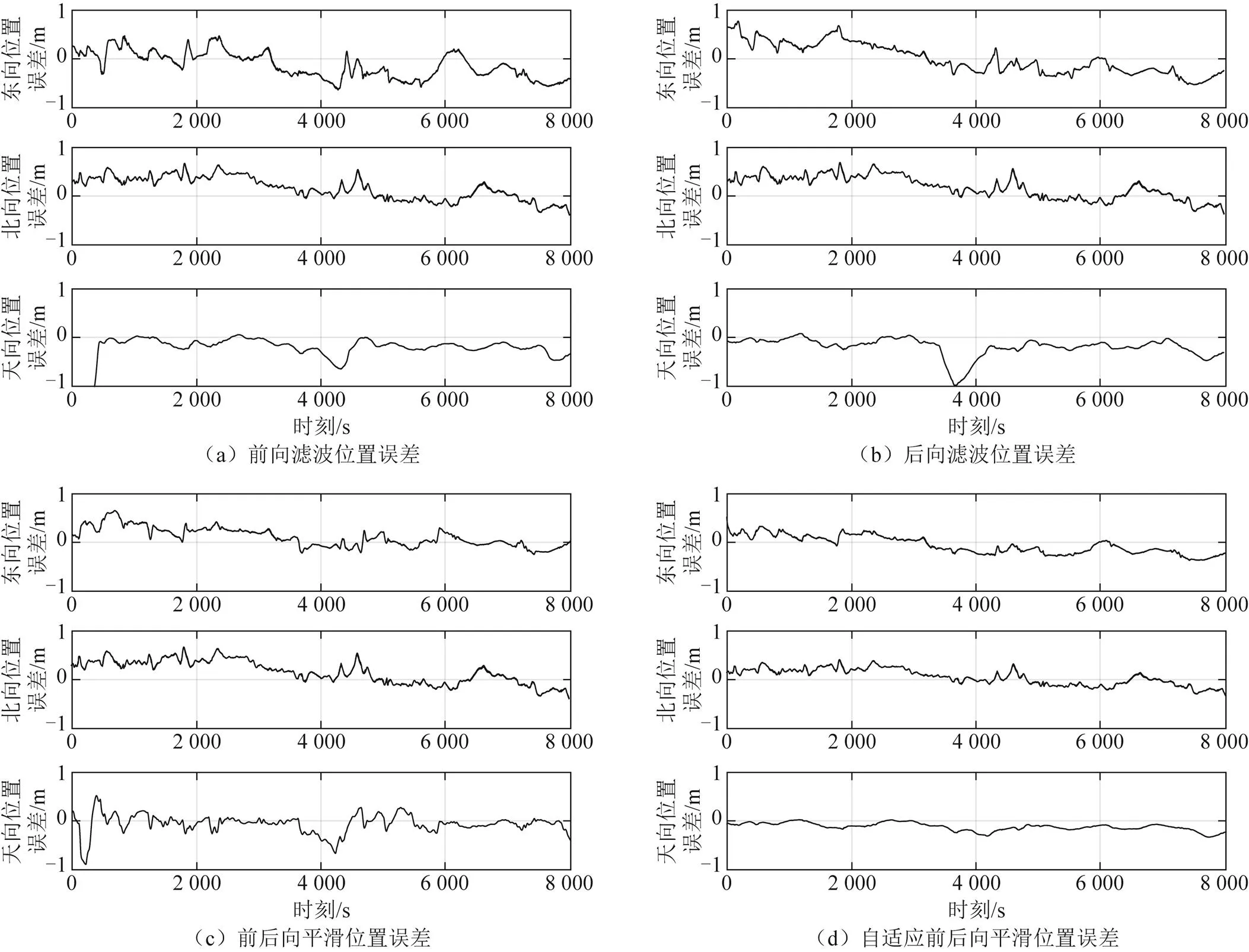
图2 4种滤波方式的位置误差

对4种模式的位置误差进行统计，采用均值误差（mean error, ME）和标准差（standard deviation, SD）对比和分析，如表1所示。相比较于单向滤波以及平滑算法，本文提出的自适应前后向平滑算法可以进一步提高位置精度和稳定性。对比平滑算法和自适应平滑算法的三维位置误差，自适应平滑算法的位置误差均值由31.95减小到25.03 cm，标准差由15.89减小到8.94 cm，精度分别提升21.66%和43.74%。

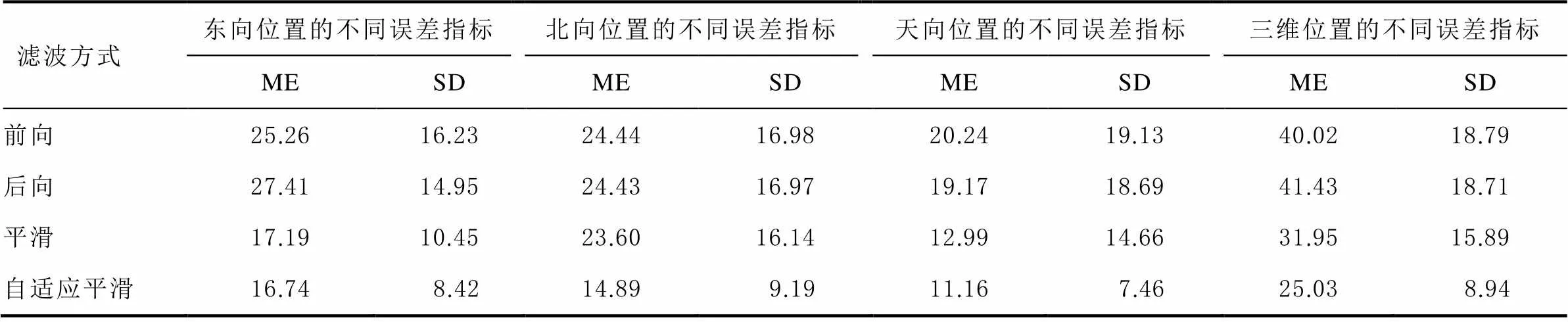
表1 位置误差统计表 cm

3.2 速度和姿态平滑效果分析

进一步对比速度和姿态的精度，图3和图4为速度和姿态的平滑算法和自适应平滑算法的误差。由图可看出，相比平滑算法，自适应平滑算法的速度和姿态精度更优。

表2为速度和姿态平滑和自适应平滑的误差均值统计情况。由表2可得出结论，采用自适应平滑算法，速度误差均值都要小于平滑算法，姿态精度略优于平滑算法。

图3 平滑和自适应平滑速度误差

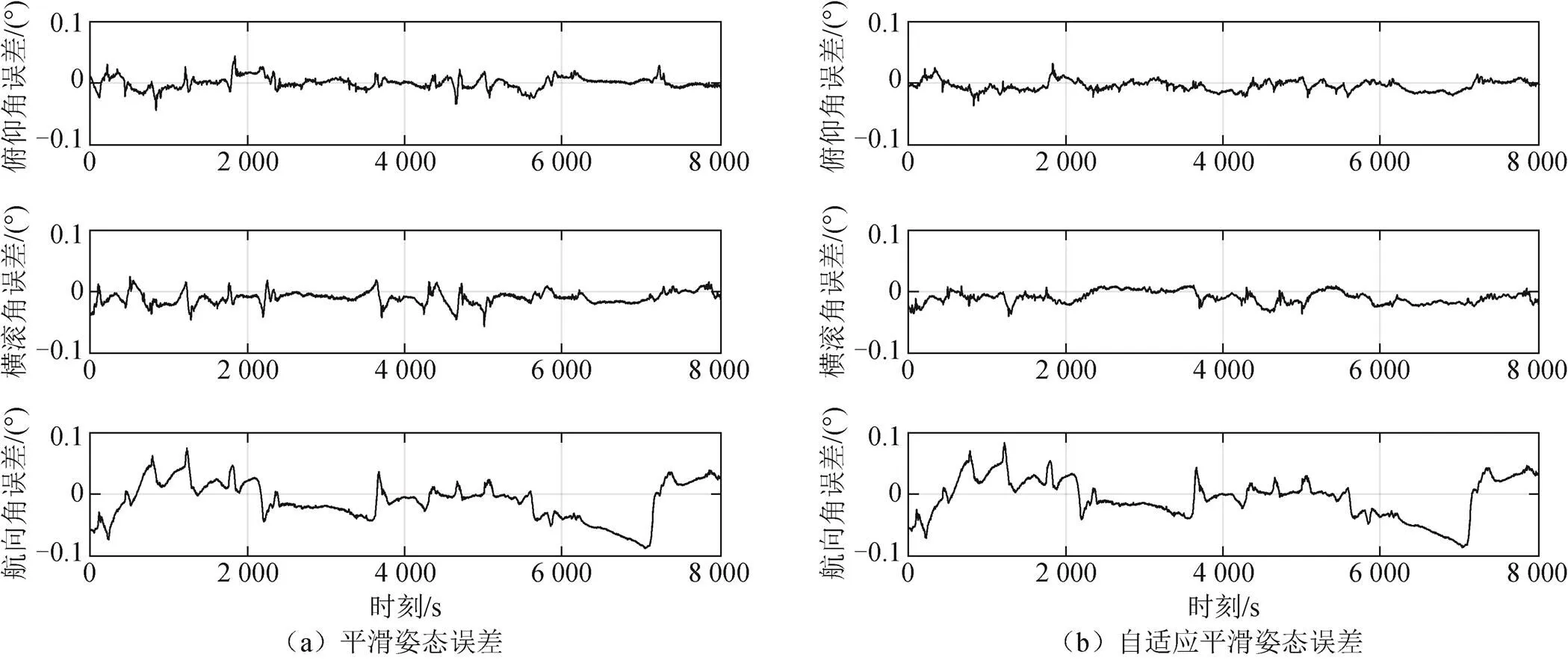
图4 平滑和自适应平滑姿态误差

表2 速度和姿态误差均值统计表

4 结束语

本文提出了一种适用于GNSS/INS组合数据后处理的自适应前后向平滑算法，算法在单向滤波中通过新息向量自适应调节观测量方差和协方差阵，以此减小GNSS误差带来的影响，最后再进行平滑，可以得到比常规前后向平滑算法更高精度的导航结果。一组实验数据计算和分析结果表明，自适应平滑算法的位置误差均值和标准差为25.03和8.94 cm，相比较于平滑算法，精度分别提高21.66%和43.74%，速度和姿态精度均有一定的提高。本文研究的是基于结构域的松组合模型，如何将自适应平滑算法应用到基于观测值域的紧组合模型中，值得进一步深入研究。

[1] GAO Zhouzheng, GE Maorong, LI You, et al. Modeling of multi-sensor tightly aided BDS triple-frequency precise point positioning and initial assessments[J]. Information Fusion, 2020, 55(1): 184-198.

[2] 袁梦飞, 阚秀, 曹乐, 等. 自适应精英遗传算法的快递车路径规划[J]. 导航定位学报, 2021, 9(6): 104-111.

[3] 张梦得, 李开龙, 胡柏青, 等. 辅助信息源短时失效下的捷联惯性基组合导航算法[J]. 兵工学报, 2020, 41(10): 2008-2015.

[4] YAO Yiqing, XU Xiaosu, ZHU Chenchen, et al. A hybrid fusion algorithm for GPS/INS integration during GPS outages[J]. Measurement, 2017, 103(2): 42-51.

[5] TAN Xinglong, WANG Jian, JIN Shuanggen, et al. GA-SVR and pseudo-position-aided GPS/INS integration during GPS outage[J]. Journal of Navigation, 2015, 68(4): 1-19.

[6] SUN Rui, ZHANG Zixuan, CHENG Qi, et al. Pseudorange error prediction for adaptive tightly coupled GNSS/IMU navigation in urban areas[J]. Gps Solutions, 2022, 26(1): 1-13.

[7] 郝万亮, 孙付平, 刘帅. 基于载波相位DGNSS/INS紧组合的平滑后处理算法[J]. 大地测量与地球动力学, 2015, 35(6): 1031-1035.

[8] 朱锋. GNSS/SINS/视觉多传感器融合的精密定位定姿方法与关键技术[D]. 武汉：武汉大学, 2019: 106-109.

[9] LIU Hang, NASSAR S, EL-SHEIMY N. Two-filter smoothing for accurate INS/GPS land-vehicle navigation in urban centers[J]. IEEE Trans. Vehicular Technology, 2010, 59(9): 4256-4267.

[10] 杨洋, 李宾, 袁泉, 等. MEMS惯导管内坐标测量的改进RTS平滑滤波算法[J]. 传感技术学报, 2021, 34(2): 189-195.

[11] 于飞飞. 基于正逆向导航解算的捷联罗经动基座初始对准方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019. DOI：10. 27061/d. cnki. ghgdu. 2019. 000854.

[12] 刘帅, 孙付平, 李海峰, 等. 前后向平滑算法在精密单点定位/INS紧组合数据后处理中的应用[J]. 中国惯性技术学报, 2015, 23(1): 85-91.

[13] ZHANG Xiaohong, ZHU Feng, TAO Xianlu, et al. New optimal smoothing scheme for improving relative and absolute accuracy of tightly coupled GNSS/SINS integration[J]. GPS Solutions, 2017, 21(3): 861-872.

[14] 刘帅. GPS/INS组合导航算法研究与实现[D]. 郑州: 信息工程大学, 2012: 38-41.

[15] 严恭敏. 捷联惯导算法与组合导航原理[M]. 西安: 西北工业大学出版社, 2019: 159-161.

Adaptive forward-backward-smoothing algorithm with application to integrated navigation

HE Maihang1, SUN Fuping2, XIAO Kai2, CHE Tongyu1, MIAO Yuewang1

（1. Troops 61363, Xi'an 710054, China; 2. Information Engineering University, Zhengzhou 450001, China）

When the signal of the global navigation satellite system (GNSS) is partially occluded or interfered, the error of the innovation vector will increase, which will increase the one-way filtering error of the GNSS/INS (inertial navigation system), and the filtering error will further interfere with the smoothing effect. In order to solve this problem, an adaptive forward and backward smoothing algorithm is proposed. The algorithm adopts adaptive Kalman filtering in one-way filtering, and adjusts the variance covariance matrix of the innovation vector adaptively to reduce the adverse effect of errors. A vehicle experimental data calculations show that the accuracy of the adaptive smoothing algorithm is better than the conventional smoothing algorithm, which can effectively reduce the error. The mean and standard deviation of the three-dimensional position error of the adaptive forward and backward smoothing algorithm are 25.03 cm and 8.94 cm, relatively, which are 21.66% and 43.74% improved than the non-adaptive processing accuracy, and the speed and attitude accuracy are also slightly improved. The proposed algorithm and experimental conclusions provide valuable reference for post-processing of integrated navigation.

forward and backward smoothing; adaptive filtering; integrated navigation; position accuracy; data post-processing

P228

A

2095-4999(2022)06-0151-06

何劢航，孙付平，肖凯，等. 自适应前后向平滑算法在组合导航中的应用[J]. 导航定位学报, 2022, 10(6): 151-156.（HE Maihang, SUN Fuping, XIAO Kai, et al. Adaptive forward-backward-smoothing algorithm with application to integrated navigation[J]. Journal of Navigation and Positioning, 2022, 10(6): 151-156.）

10.16547/j.cnki.10-1096.20220620.

2022-03-09

国家自然科学基金项目（42104034，42174047）。

何劢航（1996—），男，浙江衢州人，硕士，助理工程师，研究方向为组合导航。

孙付平（1964—），男，河南长葛人，博士，教授，研究方向为精密定位及组合导航。