具有误差补偿的信号干扰下超宽带室内定位

陈 龙，张 菁，张昊立，倪建辉，高 典

具有误差补偿的信号干扰下超宽带室内定位

陈 龙，张 菁，张昊立，倪建辉，高 典

（上海工程技术大学电子电气工程学院，上海 201620）

针对存在信号干扰的超宽带（UWB）室内精准定位问题，提出一种具有信号干扰识别和误差补偿的超宽带室内定位方法。采用拉依达准则来剔除基站与靶点之间距离数据中的异常值或缺失值；接着用最小二乘的三维定位算法求解出靶点坐标；最后利用随机反向学习策略改进的射箭算法（AA）优化支持向量机（SVM）模型来识别是否有信号干扰，并对靶点坐标进行误差补偿。实验结果表明，在信号正常的情况下，定位结果的均方根误差为20.3657 cm，比误差补偿前减小了65.1%，在信号有干扰情况下，定位结果的均方根误差为30.6871 cm, 比误差补偿前减小了57.86%。相比于传统算法，本文方法可以提高信号干扰下的超宽带室内定位精度。

超宽带；室内定位；信号干扰；支持向量机；射箭算法；误差补偿；拉依达准则

0 引言

室外定位技术主要是基于卫星导航技术（satellite navigation technology, SNT），包括全球定位系统（global positioning system, GPS）、北斗卫星导航系统（BeiDou navigation satellite system, BDS）以及伽利略卫星导航系统（Galileo navigation satellite system, Galileo）[1]。室内导航技术则主要依靠无线电定位（radio positioning, RP），包括蓝牙（blue tooth, BT）、射频识别（radio frequency identification, RFID）技术以及超宽带（ultra-wide band, UWB）等。室内定位不同于室外定位，室内由于存在墙壁、桌椅、门窗等障碍物，使得定位环境变得复杂，信号碰到障碍物会折射或散射等，导致信号不稳定[2]，因此对于室内定位存在非视距误差(not line of sight, NLOS)和信号干扰[3]。如何降低这些误差和信号干扰对定位精度的影响，已成为室内定位技术研究热点。

超宽带技术在室内定位技术中具有时间分辨率高、功耗低、利用窄带脉冲传输（narrow band pulse transmission, NPT）、稳定性好等优点，从而被广泛应用于室内定位。UWB室内定位主要的方法有基于到达角度（angel of arrive，AOA）、基于飞行时间（time of flight，TOF）、基于到达时间差（time difference of arrival，TDOA）等[4]。但在实际应用中，由于存在NLOS以及信号干扰，定位精度受到很大影响。针对这些问题，文献[5]提出了将三边测量（trilateration survey, TS）和指纹识别结合的方法，该方法能实现亚分米级的定位精度。文献[6]提出了一种鲁棒最小二乘公式，采用二阶锥松弛（second order cone relaxation, SOCR）方法拟合，提高定位精度。文献[7]通过扩展卡尔曼（）滤波，按设定的参数剔除NLOS。文献[8]综合了TDOA和AOA算法的优点，结合最陡下降算法，消除了非视距误差。文献[9]提出了一种基于自适应卡尔曼滤波算法的方法，利用视距环境构造抗差因子抑制NLOS。文献[10]采用了误差估计和补偿的方法，主要分析了实际环境UWB天线的时钟偏移、节点之间有相对速度的特点。

近年来，机器学习算法也逐渐被应用于室内定位中。文献[11]将布谷鸟搜索算法（cuckoo search, CS）与反向传播（back propagation, BP）神经网络进行结合，对TDOA进行校正。文献[12]提出一种结合免疫算法（immune algorithm, IA）和BP神经网络的 UWB 室内定位方法。文献[13]提出了基于网格搜索的支持向量机（support vector machine, SVM）和主成分分析的室内定位算法，提高了定位精度。但是，上述定位方法都是基于信号没有干扰的情况，若有信号干扰会造成测距数据出现异常值，从而使得定位误差较大。因此，信号干扰下的超宽带精确定位问题成为亟待解决的问题。

为解决信号干扰下的UWB室内精准定位的问题，提出了一种具有信号干扰识别和误差补偿的超宽带室内定位方法。首先采用拉依达（Pauta）准则来剔除基站与靶点之间距离数据中的异常值或缺失值；其次，采用最小二乘的三维定位算法，利用基站与靶点之间的距离，求解出靶点的坐标；然后，利用随机反向学习策略（random opposition-based learning, ROBL）改进的射箭算法（archery algorithm, AA）优化支持向量机的分类预测来识别是否有信号干扰；最后，利用改进的射箭算法优化支持向量机的回归预测，分别针对有干扰和无干扰2种情况进行误差补偿，将预测出的误差值补偿到最小二乘的三维定位算法的求解值中，来实现定位的误差补偿，提高定位的精度。

1 最小二乘的三维定位算法

对式（1）进行化简得

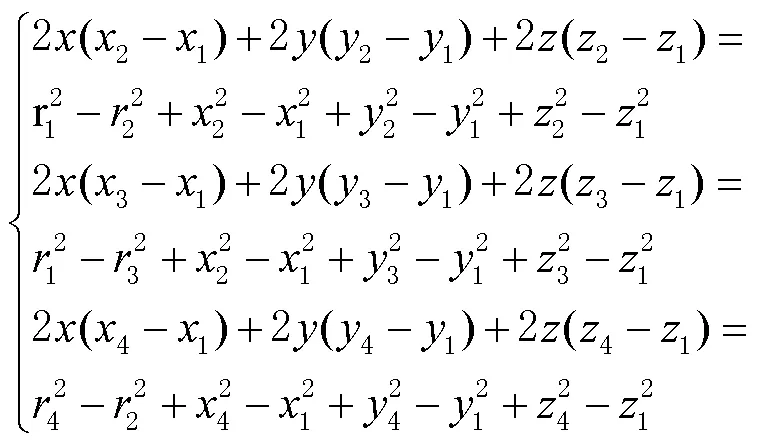
式（2）可写为矩阵形式为

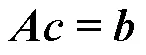
2 改进的射箭算法优化支持向量机模型

2.1 射箭算法及其改进

2.1.1 射箭算法

射箭算法是主要模仿弓箭手射击目标行为的算法。在所提出的AA中，种群中的每个成员都会根据弓箭手所瞄准的目标的指引，在搜索空间的每个维度上进行更新。种群中的每个个体都可以用一个向量来表示。该算法的种群集合可由矩阵表示为

种群中的每个个体都可以用来评价优化问题的目标函数。目标函数的值随着种群数量的变化而变化，它可以用一个向量表示为

在AA中，靶板被当做是一张白纸（正方形或长方形），它的“宽”被分割为和种群数量一样多的部分，“长”被分割为和问题变量一样多的部分。不同部分的宽度之差与个体的目标函数值之差成正比。

使用概率函数来使宽度和目标函数值成比例。该函数计算公式为

为了更新每个个体在每个维度的搜索空间中的位置，根据射箭模拟结果，随机选择一个个体。在射箭模拟中，目标函数值表现较好的个体具有较高的概率函数值，并且被选中的机会更大。累积概率已被用来模拟射箭，并随机选择一个成员。这个过程的模型为

种群个体的位置更新公式为：

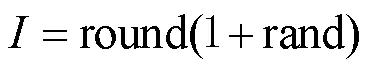
2.1.2 改进的射箭算法

由于反向学习策略无法有效增强搜索空间内种群多样性。有学者提出了改进的随机反向学习策略[14]，提高了种群多样性，增强了种群避免局部最优的能力，计算公式为

2.1.3 改进射箭算法性能测试

为了检验改进的射箭算法（improved archery algorithm , IAA）的性能，本文将IAA与AA、粒子群算法[15]（particle swarm optimization，PSO）、遗传算法[16]（genetic algorithm，GA）进行对比试验。设定种群数量为20，最大迭代次数为500，对Sphere测试函数进行求解。Sphere测试函数的收敛曲线如图1所示，其中横轴为迭代次数，纵轴为适应度值的对数log。log值越低，代表寻优精度越高。先出现曲线拐点，代表求解速度更快。4种算法在Sphere函数上的收敛曲线如图1所示。

图1 4种算法在Sphere函数上的收敛曲线

从图1可知，在求解Sphere测试函数时，IAA 算法的收敛速度更快，曲线更平滑。说明改进方法具有一定的效果。

2.2 支持向量机

SVM既可用于分类预测，又可用于回归预测。SVM通过极小化和引入拉格朗日乘子将目标函数转化为下方的对偶极小问题:

由于高斯核函数（Gaussian kernel function, RBF）拥有处理样本输入与输出之间复杂非线性关系的良好能力，而且参数选取少，计算效率高；因此将高斯核函数引入SVM中，其公式为

利用式（9）的极小化问题解出最优回归函数为

2.3 改进的射箭算法优化支持向量机模型建立

图2 IAA-SVM模型流程

3 总体定位模型的建立

3.1 数据预处理

实验采集了324个不同位置无信号干扰和有信号干扰的数据，这些数据量较大，对于这些数据需要进行清洗，删除掉一些异常、缺失、相同或相似的数据，以便于后续的定位，因此采用了拉依达准则处理这些数据。

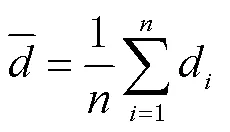
样本标准偏差公式为

3.2 模型评价指标

本模型以均方根误差（root mean square error, RMSE）作为评价指标验证模型的仿真预测效果，其计算公式为

3.3 基于信号干扰的三维定位模型建立

首先对于采集的数据进行预处理，其次利用IAA-SVM的分类预测判断该组数据是否有干扰，若有干扰，则需要建立误差补偿模型，然后用最小二乘三维定位算法求出初步坐标，再利用IAA-SVM的回归预测对最小二乘定位算法的结果进行误差补偿，最后输出三维定位坐标。总体定位模型流程如图3所示。

图3 总体模型流程

4 实验与结果分析

4.1 实验环境

如图4所示，在5000 mm×5000 mm×3000 mm的三维测试环境中，分别在4个角落0、1、2、3放置UWB锚点（anchor），锚点位置（计量单位为mm）分别为0（0,0,1300）、1（5000,0,1700）、2（0,5000,1700）、3（5000,5000,1300），锚点向所有方向发送信号。Tag是UWB标签（靶点），即需要定位的目标（只在测试环境范围内）。Tag接收到4个UWB锚点的信号（无论信号是否干扰，Tag一般都可以接收到信号），利用TOF技术，分别解算出对应的4个距离数据。

在此环境中，采集了324个不同的位置的数据。每个位置分别采集了2次，包括有信号干扰的和无信号干扰的。由于靶点在每个位置都会停留一会，所以锚点与Tag之间每0.2～0.3 s之间就会发送、接收信号一次，所以在同一位置点，UWB会采集到多组数据。

图4 实验环境示意图

4.2 数据处理结果分析

处理后324组无信号干扰和324组有信号干扰的各个锚点与靶点距离数据的样本标准差如图5、图6所示。从图5中可以看出处理后的数据样本标准差明显地减小，特别是0和3锚点，说明所用的数据处理方法是有效的。从图6可以看出，有信号干扰下的数据标准差较大，说明在有信号干扰的环境下，所采集的数据异常值和缺失值较多。

4.3 信号干扰的识别

对于信号干扰的识别，总共有648组数据，将518组数据作为训练集，其中，有信号干扰259组数据和无信号干扰的259组数据。将其中130组数据作为测试集，有信号干扰65组数据和无信号干扰65组数据。数据分类结果如图7所示，其中，类别标签1代表有信号干扰，类别标签2代表无信号干扰。从图中可以看出IAA-SVM的分类准确率为93.1%，SVM分类的准确率为90%，说明IAA-SVM的分类效果较好。

图7 各模型分类结果与真实值对比

4.4 最小二乘三维定位结果

采用最小二乘三维定位算法分别对有信号干扰数据和无信号干扰数据进行求解。对于无信号干扰情况下的靶点坐标求解结果和真实值的对比如图8所示，对于有信号干扰情况下的靶点坐标求解结果和真实值的对比如图9所示。

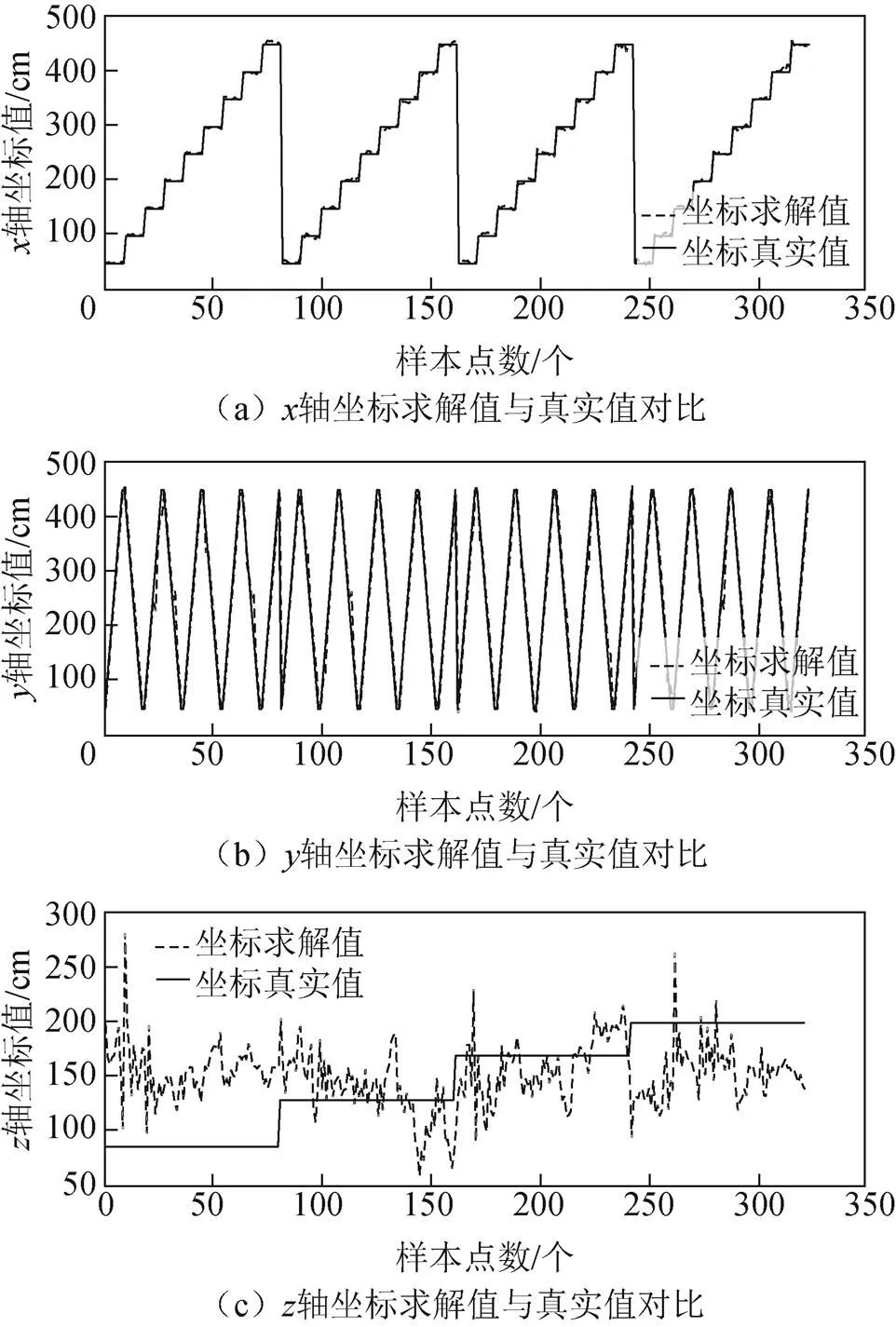
图8 无信号干扰各轴坐标求解结果

图9 有信号干扰各轴坐标求解结果

从图8可以看出在无信号干扰情况下，最小二乘的三维定位算法对于轴和轴的求解结果较为准确，但是轴的求解结果误差较大。从图9可以看出在有信号干扰情况下，最小二乘的三维定位算法对于、、轴的求解结果均和真实值有较大误差，尤其是轴的误差最大，各坐标轴在有信号干扰下的RMSE和无信号干扰下的RMSE如表1所示，可以看出轴的RMSE比其他2个坐标轴大很多。因此需要利用IAA-SVM误差补偿模型对无信号干扰下的轴和有信号干扰下的、、轴进行误差补偿。

表1 不同预测模型仿真误差指标 cm

4.5 误差补偿

将各锚点坐标作为输入，每个位置靶点坐标的求解值与真实值的误差作为输出进行训练，这样就建立起误差补偿模型。用训练好的模型来预测求解值与真实值的误差，然后将误差补偿到求解值当中，就完成了误差补偿的过程。

1）无信号干扰情况下的结果。在无信号干扰情况下，只需对轴进行误差补偿。对于轴的误差预测结果以及和支持向量机、极限学习机（extreme learning machine, ELM）预测结果对比如图10所示。其中，IAA-SVM的RMSE为20.3657 cm。从图10可以看出，IAA-SVM模型对于误差的预测与真实误差较为吻合，比其他2种模型预测效果好，其中IAA-SVM的RMSE为20.3657 cm，SVM的RMSE为30.3612 cm，ELM的RMSE为40.8967 cm，说明本文IAA-SVM误差补偿模型优于其他2种模型。

误差补偿后的轴坐标值与补偿前的坐标值对比如图11所示。

图10 不同模型z轴误差预测结果比较

图11 z轴无信号干扰误差补偿前后的对比

2）有信号干扰情况下的情况。有信号干扰情况下，、、轴都需要补偿，其中对于轴的误差预测结果如图12所示。从图12可以看出，IAA-SVM模型对于有信号干扰情况下轴误差的预测与真实误差较为吻合，其中，IAA-SVM的RMSE为25.3679 cm，SVM的RMSE为40.1637 cm，ELM的RMSE为50.9842 cm。误差补偿后的、、轴坐标值与补偿前的坐标值对比如图13所示，以及各坐标轴补偿前与补偿后的RMSE对比如表2所示。

图12 不同模型z轴误差预测结果比较

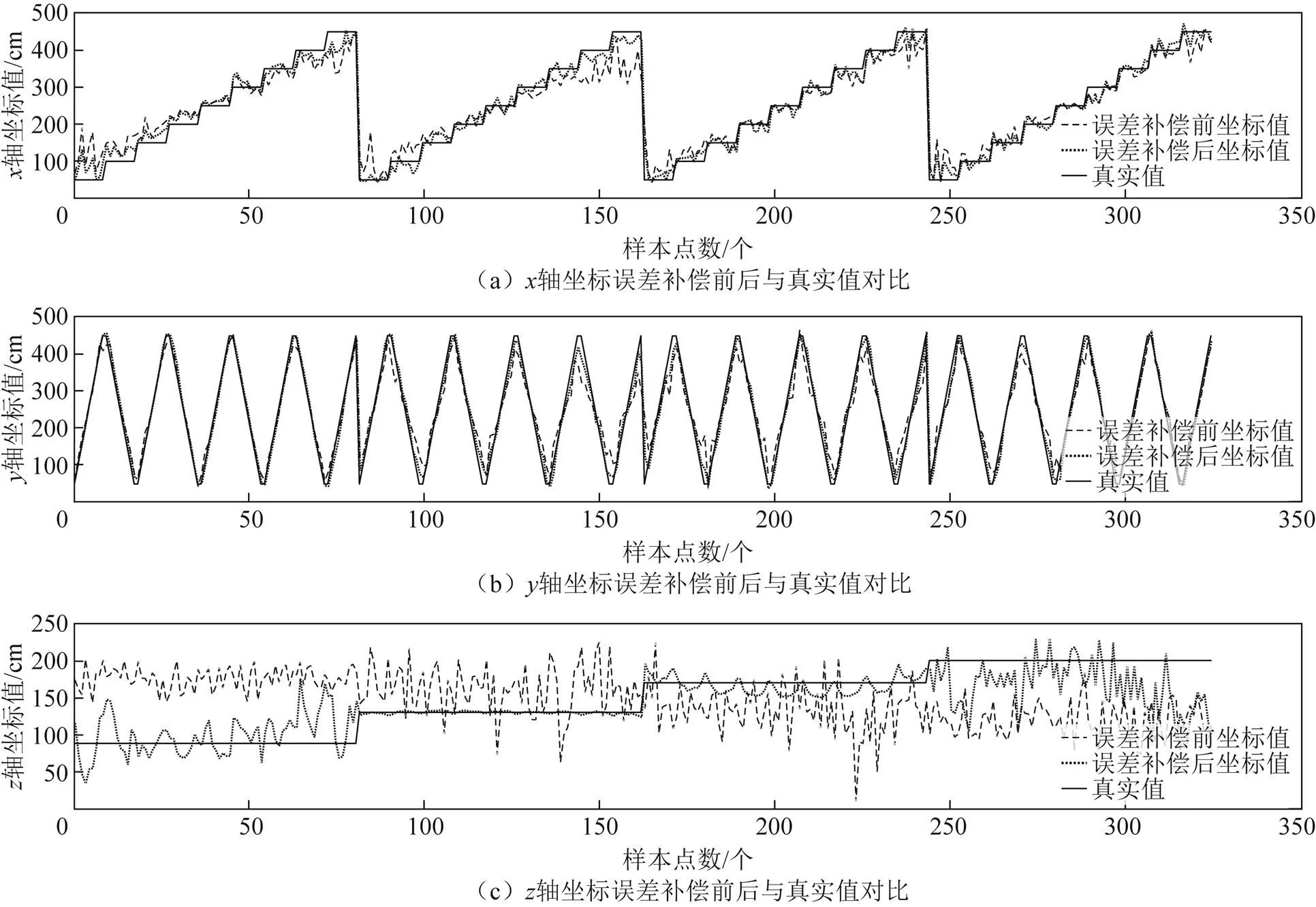
图13 有信号干扰误差补偿前后的对比

表2 信号干扰下各轴坐标误差补偿前后RMSE对比 cm

从图13可以看出，在有信号干扰情况下，无论、、轴，误差补偿后的坐标值都比误差补偿前的坐标值更接近真实值。从表2可以看出，各坐标轴误差补偿后的RMSE都比误差补偿前的小。以上都说明，本文的误差补偿方法是有效的。

5 结束语

为了解决存在信号干扰的UWB室内精准定位问题，本文提出了一种基于改进的射箭算法优化支持向量机的具有信号干扰识别和误差补偿的室内定位模型，不仅实现了信号正常情况下的精准定位，还实现了有信号干扰情况下的准确定位。实验结论如下：

1）对于数据处理，本文使用的拉依达准则和余弦相似度能够有效地剔除数据中的异常值和缺失值，处理后的数据样本标准差明显减小，便于后续定位使用。

2）对于信号干扰的识别，本文提出的基于改进的射箭算法优化支持向量机分类模型的信号识别准确率达到93.1%，分类结果准确。

3）对于最小二乘的三维定位结果的误差补偿，在无信号干扰情况下，补偿后坐标值的均方根误差比补偿前减小了65.1%。有信号干扰情况下，补偿后坐标值的均方根误差比补偿前减小了57.86%。说明本文的误差补偿方法是有效果的。

4）本文所构建的改进的射箭算法优化支持向量机的误差补偿模型无论在有信号干扰和无信号干扰情况下，误差补偿效果都优于其他模型。

[1] 董佳琪,连增增, 徐精诚, 等. 融合卡尔曼滤波算法在超宽带定位中的研究[J/OL]. 测绘科学. (2021-11-09) [2022-05-22]. https: //kns.cnki.net/kcms/detail/11.4415.P. 20211109.1424. 002.html.

[2] 齐小刚, 陈谌, 李芷楠．室内定位中非视距的识别和抑制算法研究综述[J]．控制与决策, 2022, 37(8): 1921-1933.

[3] 徐爱功, 张涵, 宋佳鹏, 等. 利用UWB/LiDAR里程计的室内高精度定位方法[J]. 测绘科学, 2022, 47(2): 1-7, 38.

[4] 缪希仁, 范建威, 江灏, 等. 基站异常情况下基于改进极限学习机的超宽带室内定位方法[J]. 传感技术学报, 2020, 33(10): 1457-1466.

[5] DJOSIC S, STOJANOVIC I, JOVANOVIC M, et al. Fingerprinting-assisted UWB-based localization technique for complex indoor environments[J]. Expert Systems with Applications, 2021, 167: 265-274. DOI:10.1016/j.eswa.2020. 114188.

[6] GAO S C, ZHANG S J, WANG G, et al．Robust second-order cone relaxation for TW-TOA-based localization with clock imperfection[J]. IEEE Signal Processing Letters, 2016, 23(8): 1-5．

[7] 徐爱功, 刘韬, 隋心, 等．UWB/INS紧组合的室内定位定姿方法[J]导航定位学报, 2017, 5(2): 14-19.

[8] SHEN C, WANG C X, ZHANG K, et al. A time difference of arrival/angle of arrival fusion algorithm with steepest descent algorithm for indoor non-line-of-sight locationing[J]. International Journal of Distributed Sensor Networks, 2019, 15(6): 497-506.

[9] 刘韬, 徐爱功, 隋心．基于自适应抗差卡尔曼滤波的UWB室内定位[J]. 传感技术学报, 2018, 31(4): 567-572．

[10] 李荣冰, 王念曾, 刘建业, 等. 面向相对导航的UWB测距误差估计与补偿方法[J]. 仪器仪表学报, 2019, 40(5) : 28-35.

[11] LI N, SHEN C, ZHAN K, et al. The TDOA algorithm based on BP neural network optimized by Cuckoo search[C]//The Institute of Electrical and Electronic Engineers（IEEE）. Proceedings of the 2020 International Conference on Robots and Intelligent System. Palms Springs: IEEE, 2019: 539-542[2022-05-22].

[12] 李勇, 柳建. 基于IA-BP神经网络的UWB室内定位系统[J]. 电子测量技术, 2019, 42(5): 109-112.

[13] ZHANG L W, LI Y S, GU Y J, et al．An efficient machine learning approach for indoor localization[J]．China Communications, 2017, 14(11): 141-150．

[14] LONG W, JIAO J J, LIANG X M, et al. A random opposition-based learning grey wolf optimizer[J]. IEEE Access, 2019, 7: 113810-113825.

[15] 李爱国, 覃征, 鲍复民, 等. 粒子群优化算法[J]. 计算机工程与应用, 2002(21): 1-3, 17.

[16] 胡兵, 詹仲强, 陈洁, 等. 基于PCA-GA-Elman的短期光伏出力预测研究[J]. 太阳能学报, 2020, 41(6): 256-26.

UWB indoor positioning under signal interference based on error compensation

CHEN Long, ZHANG Jing, ZHANG Haoli, NI Jianhui, GAO Dian

（School of Electric and Electronic Engineering, Shanghai University of Engineering Science, Shanghai 201620, China）

Aiming at the problem of ultra-wide band (UWB) indoor accurate positioning with signal interference, proposes an ultra-wide band indoor positioning model with signal interference identification and error compensation proposed. Firstly, for the abnormal values in the distance data between the base station and the target, uses the pauta criterion to deal with it. Secondly, uses the three-dimensional positioning algorithm of least square to solve the target coordinates; Finally, the improved archery algorithm (AA) based on random reverse learning strategy is used to optimize the support vector machine (SVM) model to identify whether there is signal interference and compensate the error of target coordinates. The experimental results show that when the signal is normal, the root mean square error of the positioning result is 20.3657 cm, which is 65.1% less than that before error compensation. When the signal is disturbed, the root mean square error of the positioning result is 30.6871 cm, which is 57.86% less than that before error compensation. Compared with the traditional algorithm, this method improves the UWB indoor positioning accuracy under signal interference.

ultra-wide band; indoor positioning; signal interference;support vector machine;archery algorithm; error compensation; Pauta criterion

P228

A

2095-4999(2022)06-0059-09

陈龙，张菁，张昊立，等. 具有误差补偿的信号干扰下超宽带室内定位[J]. 导航定位学报, 2022, 10(6): 59-67.（CHEN Long, ZHANG Jing, ZHANG Haoli, et al.UWB indoor positioning under signal interference based on error compensation[J]. Journal of Navigation and Positioning, 2022, 10(6): 59-67.）

10.16547/j.cnki.10-1096.20220608.

2022-06-22

陈龙（1997—），男，江苏南京人，硕士研究生，研究方向为室内定位导航。

张菁（1969—），女，上海人，硕士，副教授，研究方向为人工智能及大数据在电气控制中的应用。