循环水泵轴弯曲原因分析

李兆瑜，李 易，刘达锋，张可欣

（广州汇锦能效科技有限公司，广州 510660）

循环水泵作为一种重要的电厂辅机，其运行工况直接影响电厂机组设备性能。在实际运行过程中，循环水泵泵轴可看作是一种挠性转子的旋转机械。由于循环水昼夜温差大，机组运行负荷率、运行环境温度实时变化或机械性原因等不稳定因素[1]，旋转机械最易出现不同程度的振动问题，造成水泵可靠性、水力性能的降低和引发水力噪声，进而影响电厂机组设备的经济、安全运行[1-3]。

在水泵运行中产生振动的各种问题中，主要包括部件质量分布不均、轴偏离和螺栓受力不平衡等机械性原因，以及水力作用或电磁力作用引发水泵的强烈震动[4]。由于水泵振源的多样性，使得水泵振动特性的分析因素较为复杂。因此，对水泵振动特性的监测和分析有利于提高泵组可靠性和水泵的安全运行，并对旋转机械故障诊断具有重要的理论意义和工程价值[5]。目前实际工程上关于水泵常用的振动分析方法主要是现代数值计算方法和频谱分析方法[6]。其中，现代数值计算方法通过对水泵系统发生故障部分建立数学模型，分析不同的参数变化找到故障原因。基于信号处理的频谱分析方法，利用传感器采集到的水泵运行数据分解为振动信号频谱图，从而直观观察到振动故障信息，具有不用建立繁杂数学模型、适应性强等优点。但目前的研究中，还未考虑固有性质、不平衡力的频率变化、水击现象在水泵振动问题和共振原因研究中的对比分析[7-9]。

本文以某电厂立式循环水泵为研究对象，其在运行中出现振动突然大幅度增大（超过能测量振动值），电流随时大幅度增大（超过能测量电流），轴弯曲的振动问题。水泵停止运行后，现场发现上部泵壳破碎、泵轴弯曲及中间轴承支架断裂。通过对循环水泵轴震动、水击校核及对水泵在额定工况下运行进行分析和计算，得出轴的固有频率、偏心距和截面最大水头值，以期通过震动、水击发生的物理原因、过程及传播方程的简要分析，找出水泵振动问题和共振原因。

1 固有性质对振动特性的影响

1.1 水泵的材料和物性参数

本文以某电厂的循环水泵为研究对象，其型号为88LKXA-17。循环水泵为立式轴流式，不考虑因重力作用而产生的初始弯曲。水泵轴的材料为不锈钢0Cr17Ni12Mo2，一般应用于海水和其他各种介质中，耐腐蚀性较好。该不锈钢的纵向弹性模量E为19.6×1010N/m2，密度为7 980 kg/m3。水泵的轴长（未考虑叶轮室段轴的长度）为10.465 m，泵轴直径为220 mm；额定工况下轴的外加扭转力偶矩直接传递自电机的扭转矩为53780.7Nm。水泵的转速为370 m/s，流量为10.3 m3/s，扬程为17 m。水泵参数见表1。

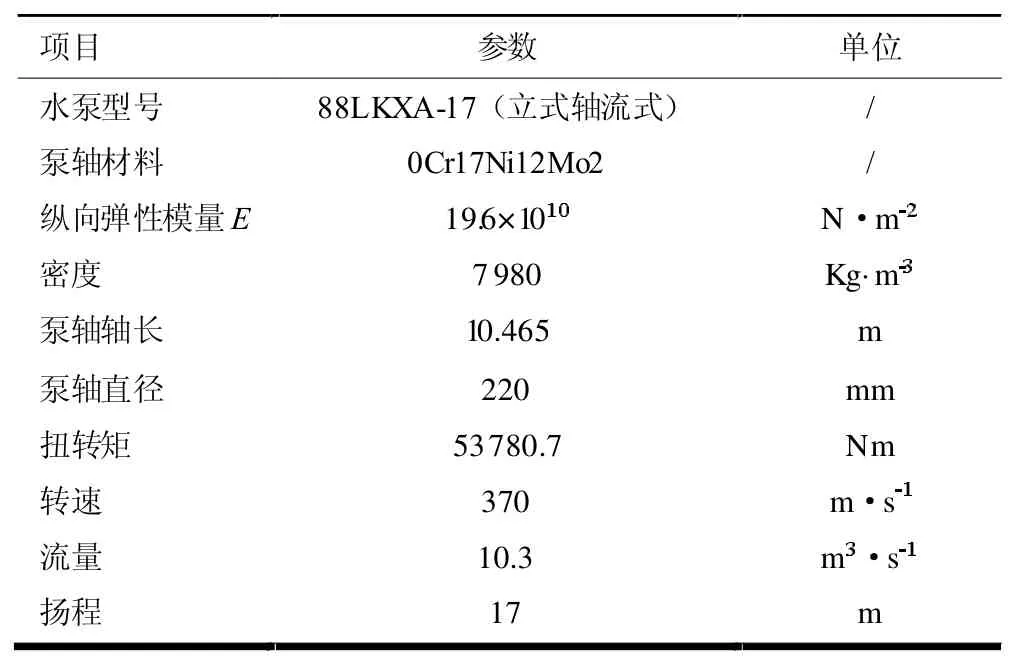
表1 立式循环水泵参数

1.2 水泵固有性质对振动特性的影响

不考虑不平衡力和泵轴上存在附着物的影响，水泵泵轴的安装完全对心并且泵轴本身不存在质心偏移，那么轴的旋转可以看成是两端自由的对称均匀系统[10]，因此泵轴的临界转速及固有函数计算如下所示。

固有频率为

固有函数为

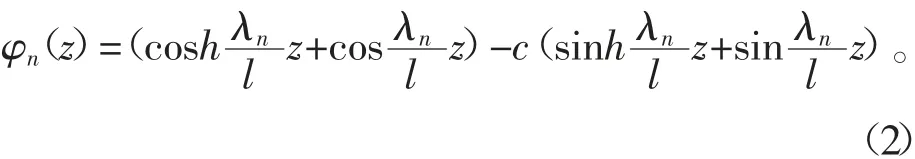
计算挠曲为

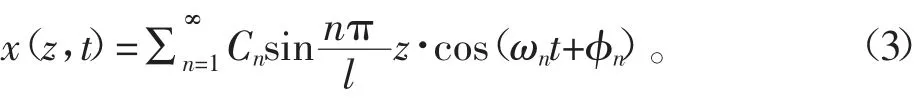
式（1）、式（2）、式（3）中：n为阶数；l为轴的总长度；z为与原点的距离；E为纵向弹性模量；I为轴的截面惯性矩；μ为单位轴向长度的转子质量；cosh和sinh分别为双曲余弦函数和双曲正弦函数sinh（x）=（ex-e-x）/2，cosh（x）=（ex+e-x）/2；t为周期；Cn为第n阶的振幅；Φn即φn（z）；c和λn为固有值，其值见表2。

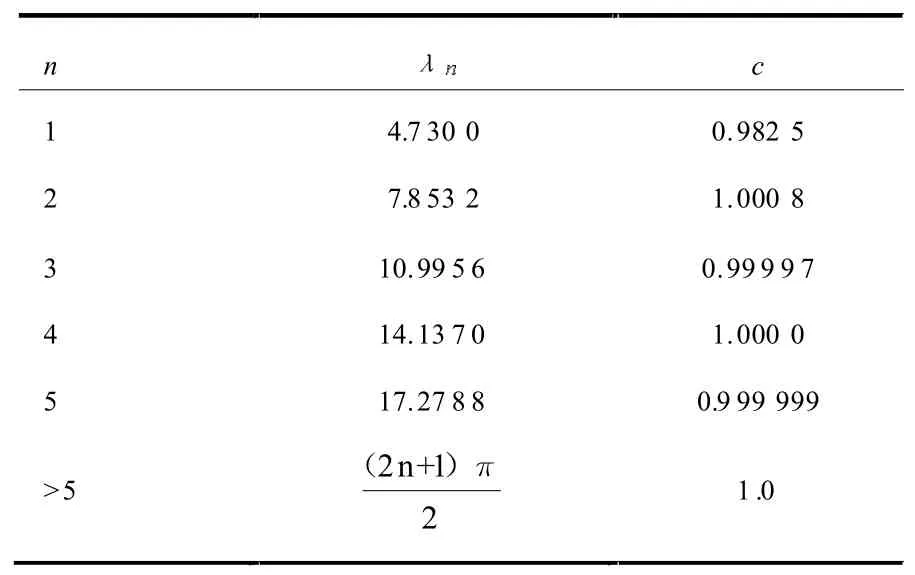
表2 不同固有性质的特性参数

由上可以知道：

轴的总长度l=10.465 m（未考虑叶轮室段轴的长度）；

纵向弹性模量E=19.6×1010N/m2；轴的界面惯性矩

单位轴向长度转子质量μ=ρD=303.192 1 kg/m。

那么可以求得

当n=1时，

固有频率ω1=55.685 3 Hz；

其振动曲线如图1所示。

图1 水泵沿轴向振动曲线（n=1）

由于Cn、ϕn由振动的初始条件决定，因此，上图的纵坐标仅为振型，其数值不具有意义，不能代表振幅。

当n=2时，

固有频率ω2=153.498 5 Hz；

其振型曲线如图2所示。

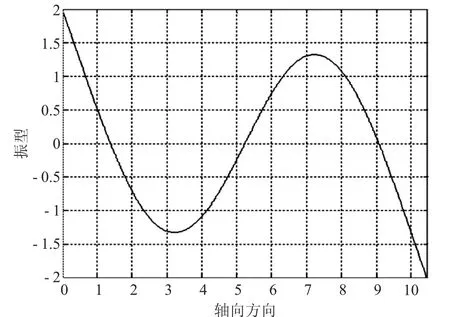
图2 水泵沿轴向振动曲线（n=2）

由此得出，在水泵的工作转速区域内，水泵的工作频率f≤（1.2×370/60）=7.4 Hz，其水泵的工作频率（赫兹数）远小于第一阶共振频率。因此，可以认为在不考虑其他不平衡力的情况下，水泵在安全工作转速之内，不会发生共振现象。

2 不平衡力对振动特性的影响

在实际运行过程中，循环水泵泵轴可看作是一挠性转子的旋转机械。由于在旋转机械中的运动部件部分存在加速度，产生的惯性力（旋转质量的离心力等）引起振动、噪声或自身性能下降外，在机械的运动部分内部的不平衡力将作为动载荷作用于接卸的静止部分，从而造成静止部件的损坏。此外，在挠性转子旋转过程中，由于不平衡离心力的作用，其轴线将做空间挠曲线振摆运动，并且轴挠曲的形状及大小随转速而变化。即使在某一转速下转子平衡到支承动载荷或支承振动为零，当转速发生变化也会破坏存在的平衡状态。所谓旋转转子的平衡，就是使转子的质量分布变成完全平衡状态的一种操作。处于不平衡状态的一般转子，如果从平衡操作的观点来看，可以理解为具有“完全平衡状态+质量偏差的”的质量分布的转子。

因此，旋转转子的不平衡力，往往来自于质量偏差产生的离心力，离心力的表达式为

式中：ω为轴的转速，用频率表示，s-1；M为旋转转子的总质量，kg；e为质心偏移距离，m；P为离心力；N；U为不平衡量，kg·m。

但是，由于中间支撑轴承之间容易损坏，可能造成轴的摆动或者其他原因引起不平衡力导致轴的质心偏移，使得泵轴的振动幅度加剧。

为了方便研究轴的质心偏移，假设：

（1）在轴长表面在单边，均匀分布m˙=0.5 kg/m的不平衡质量，那么可以知道单位轴向长度上的不平衡为u=m˙R=0.5×0.11=0.055 kg。

那么，轴的总不平衡量可以为

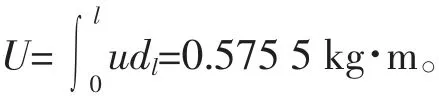
根据不平衡量的表达式得出质心偏移量为

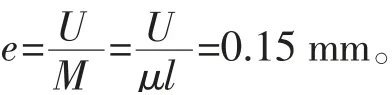
此时的偏移量远远小于轴的直径，基本上可以忽略不计。

（2）在轴上的某一处，分布着m=5 kg的不平衡质量。

那么，轴的总部平衡量可以为

质心偏移量为

此时的偏移量也远远小于轴的直径，基本上可以忽略不计。

（3）由于不平衡力的存在，此旋转轴的动态挠性曲线的形状r（l）可以由下式表示

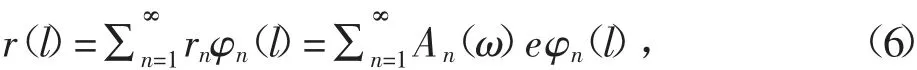
式中：n为阶数；φ为旋转轴的固有函数；e为偏移量；An为动态放大系数；r为动态挠性曲线的形状，是轴长l的函数；φ即φn（l），为轴长l的函数。

这里着重讨论An，若是动态放大系数越大，则表示由于不平衡量的存在而导致振动的加剧程度越高；反之，则振动程度越低。

动态放大系数An（ω）取决于ω/ωn的大小，具体情况如下。

（1）若ω≈ωn时，An（ω）=∞；

（2）若ω≪ωn时，An（ω）≈0；

（3）若ω≫ωn时，An（ω）≈1。

水泵的运行速度为370 r/min，远远小于轴的一阶固有频率，因此属于情况（2）。即便有不平衡量的存在，对振动的加剧造成的影响也可以认为是忽略不计的。

3 水力原因对振动特性的影响

本文以特征线法计算管道水力压力。

管道上游一般为水库或压力前池，其水位变化较小，可以忽略。故在水击计算中通常认为其水位为不变的常数。此时，存在有

式中：Hu为己知的水库水位或前池水位。

j时刻管道上游进口节点的流速为

管道出口时刻j管道末端节点的水头和流速为。

式中：τj为j时刻管道末端阀门相对开度，τj=-0.043（Δt·j）+1。

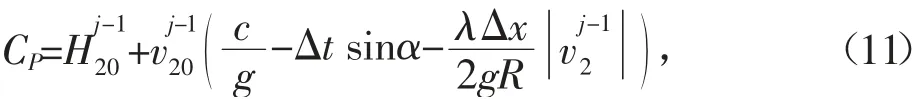
其中，阀门在恒定流状态下管道末端的水头为

除进口和出口外，其余各截面的计算公式为

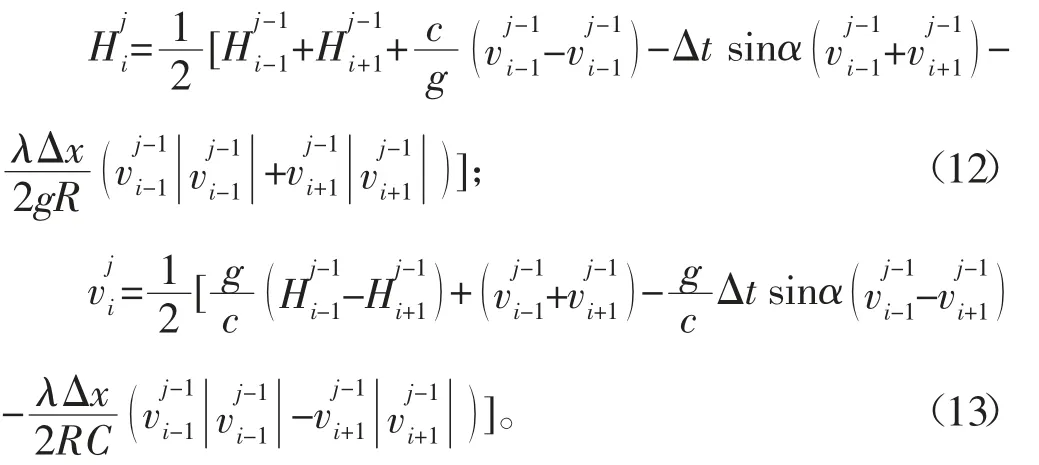
首先根据初始条件，即管道上j=1时刻，管道i个节点（断面）的v与H的初始值。利用式（7）和（8）可以求得时刻j=t/Δt除边界节点意外的各节点值，即编号为i的节点上的同时由上游的边界条件式与沿特征线c-的式可以求得上游边界i=1处的由下游的边界条件式与沿特征线c+的式可以求得下游边界处的值。

将t=Δt时刻各结点的流速、水头值作为已知值，重复上述步骤，可以计算t=2Δt，3Δt，…等时刻各结点的流速、水头值，见表3。

表3 各截面出现的H最大值及与初始值的比值

计算结果表明，某一截面出现的最大水头数值达到阀门关闭前该截面处水头值，与初始值的比值达到了48.39，短时间内对水泵产生极大的冲击。因此，水击可能是造成水泵泵轴发生弯曲的最主要原因。

4 结论

本文针对立式循环水泵泵轴的断裂问题，从固有性质、不平衡力和水力原因3方面对水泵的振动问题和泵轴断裂原因进行了研究，得到以下结论：

（1）针对水泵固有性质对振动特性的分析，由于水泵的轴的固有频率较大，最小的一阶固有频率为ω1=55.685 3 Hz，而循环水泵的运行转速较低，ω=370 r/min≈6~7.4 Hz，远远小于轴的一阶固有频率，因此，形成共振的可能性较小。

（2）通过不平衡力对振动特性的分析，5 kg的附着物造成的质心偏移仅有0.1 mm左右。即使泵轴的外表面存在不平衡量，但由于泵轴的重量较大，对泵轴产生的质心偏移量较小，其影响忽略不计。因此，可初步判断水泵轴在正常运行范围内共振所造成的影响较小。

（3）通过水力原因对振动特性的分析，认为可能是因机组运行负荷率的变化，短时间内截面的水力压力达到了初始值的48.39倍，对水泵产生极大的冲击力造成泵轴的弯曲。

该研究结论适用于相似泵站、泵组出现振动问题情况的对比分析，有利于防止水泵出现严重振动影响电厂的经济、安全运行。