基于环路增益的直流微网母线阻抗在线估计和阻尼方法

高杉雪，杨鑫，沈纹冰，仲卫 ，张帅，汪敏

（1.云南电网有限责任公司昆明供电局，云南 昆明 650011；2.国电南瑞南京电网调控技术分公司，江苏 南京 211100；3.华中科技大学电气学院，湖北 武汉 430074）

众多分布式能源（distributed energy resourc⁃es，DER），如太阳能电池板和储能系统，可利用电力电子变换器有效地集成到直流微电网中[1]。通常，DER转换器的控制器由多个控制回路组成，每个回路的设计目的是为该独立转换器提供一定的动态性能[2-3]。然而，源侧变换器和负载变换器的相互连接会影响这些回路的动态行为，这种现象通常被称为变换器相互作用[4]。变换器运行特性受互连变换器的数量、拓扑结构和控制回路特性而改变，这反过来又会影响某些控制回路的动态性能。不稳定变换器相互作用的一个常见例子是反馈控制的负载功率变换器，它在直流母线的输入端表现为恒定的功率负载（constant power load，CPL）。CPL变换器在其电压回路带宽内呈现负的增量阻抗，这被认为具有失稳效应，导致子系统相互作用[5-7]。DER变换器控制回路动态性能变化的另一个例子是船载直流配电系统，这是由于从其终端看到的阻抗变化造成的。在这种情况下，当系统配置在舰船任务期间发生变化时，变换器从负载端和源端看到的行为可能会发生显著变化。因此，互联的电力变换器系统存在稳定性问题。为解决上述问题，可对直流微网稳定性进行连续在线监测，并增加进一步的自适应控制或调整动作，以确保直流微电网的可靠运行。

图1为直流微电网的典型结构图，其中，多转换器系统被划分为1个源侧子系统和1个负载子系统。

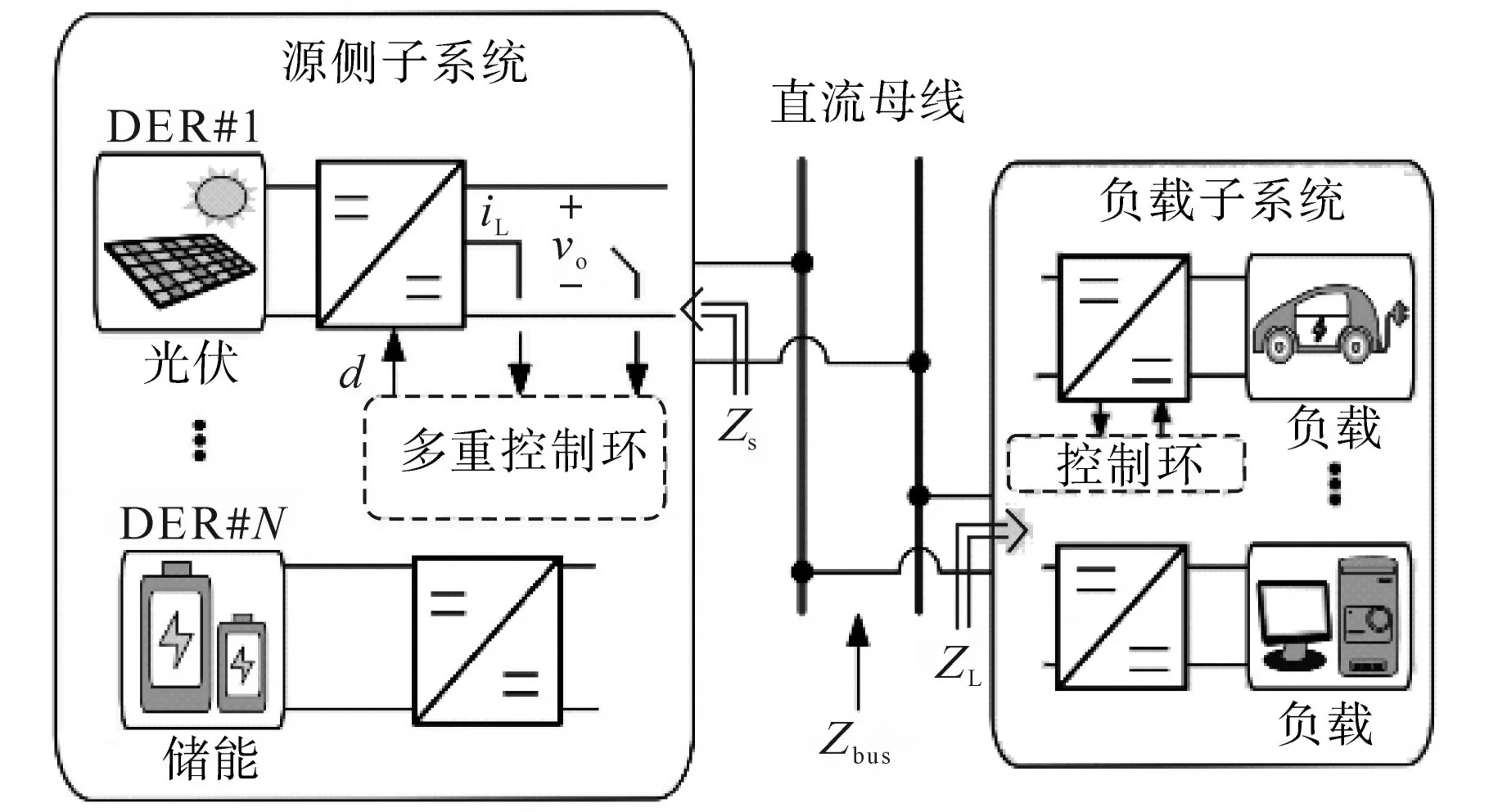
图1 具有多个电力电子变换器直流微电网的典型结构图Fig.1 Typical DC microgrid with multiple power electronic converters

这种系统的相互作用稳定性在文献[8]中首先提出了解决方法。源侧子系统阻抗Zs与负载子系统阻抗ZL之比称为小环路增益，是许多小信号稳定性研究的基础。基于小环路增益，一些研究提出了不太保守的稳定性准则。文献[9]针对基于阻抗的稳定性分析方法存在的一些局限性，如组件分组灵敏度、潮流方向等，提出了基于无源的稳定性判据（passive-based stability criterion，PBSC）。该准则连同允许阻抗区域准则（allow⁃able impedance region，AIR），仅通过观察直流母线阻抗来评估电力转换系统的稳定性。如图1所示，总线阻抗Zbus被定义为源侧子系统阻抗Zs和负载子系统阻抗ZL的并联组合。PBSC和AIR原则不仅能够评估一个互联系统的小信号稳定，还可以研究其动态性能，并辅助设计一个稳定控制器[10]。通常Zbus在Zs的大小与ZL相当时出现共振峰。为了抑制这一高峰，提高稳定性，目前主要有2种方法：一是增加负载变换器的控制器，如增加一个前馈控制器[11]，以消除母线阻抗幅值的峰值；二是通过作用于源侧变换器、通过调整现有控制器[12]或通过在控制环中添加一个阻尼项来抑制母线阻抗的高峰共振[13]。上述母线稳定方法都是基于母线阻抗测量，这需要对不同的电源和负载转换器进行测量。文献[14]提出了一种更简单的方法来实现这一过程，即在源侧变换器的数字控制器中执行所有的扰动测量。为此，测量了源侧变换器的电压回路增益和母线侧阻抗，并在此基础上估算了母线阻抗。虽然该方法简化了基于总线阻抗的稳定性分析，但仍然需要测量大量数据序列，并进行傅里叶变换[15-18]。

为了解决上述问题，本文首先提出对源侧变流器电压或下垂回路的相位裕度进行监测，然后根据监测到的相位裕度估计母线阻抗的峰值。接着，假设总线阻抗共振是在电压或下垂环的带宽附近，并被用来估计基于电压或下垂环的相位裕度的峰值总线阻抗。在一般控制回路正常运行时注入小信号扰动，并调整注入频率，直到达到单位回路增益频率（即交叉频率）。在此频率，扰动前后信号之间的相移产生相位裕度。在根据相位裕度估计母线阻抗峰值后，通过自调整电压回路控制器增益来抑制峰值，以满足PBSC和AIR原则的要求。

1 基于环路增益的母线阻抗

1.1 源侧变换器的环路增益

根据图1，母线阻抗Zbus定义为源侧子系统阻抗Zs与负载子系统阻抗ZL的并联组合：

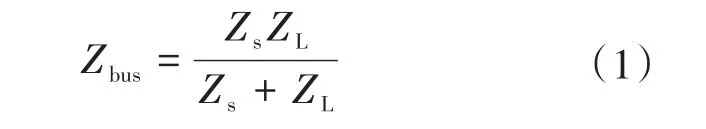
为了满足PBSC，Zbus必须不包含任何右半平面极点；此外，对于所有频率，Zbus的实分量必须为正。这相当于有母线阻抗的相位限制在-90°和+90°。通用DER变换器的典型多回路控制结构如图2所示。

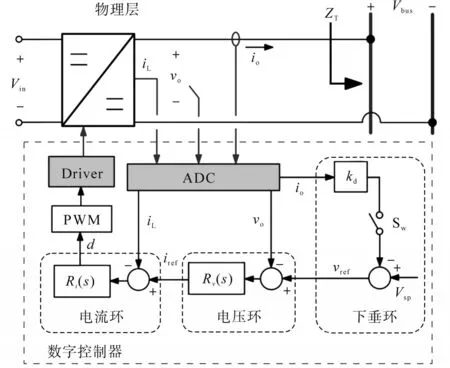
图2 直流微电网DER的通用变换器控制方框图Fig.2 Generic converter control block diagram of DC microgrid DER

特别是电感电流iL和输出电压vo需要被考虑。如果开关Sw打开，则考虑恒定的参考电压vref=Vsp。为了在并行DER之间实现功率分配，开关Sw可以被关闭，从而使下垂回路vref=Vsp-kdio。图2中，kd为下垂系数，io为输出电流，Ri（s）为电感电流和输出电压稳压器，Rv（s）通常是为标称负载设计的。然而，在另一个源和连接到直流母线的负载变换器的相互作用下，某些回路的动态行为可能会偏离设计的性能。为了说明这一点，本文用ZT表示从直流母线的转换端子看到的整体阻抗。图2中的变换器控制方框图如图3所示，其中微电网的其余部分用等效阻抗ZT表示。

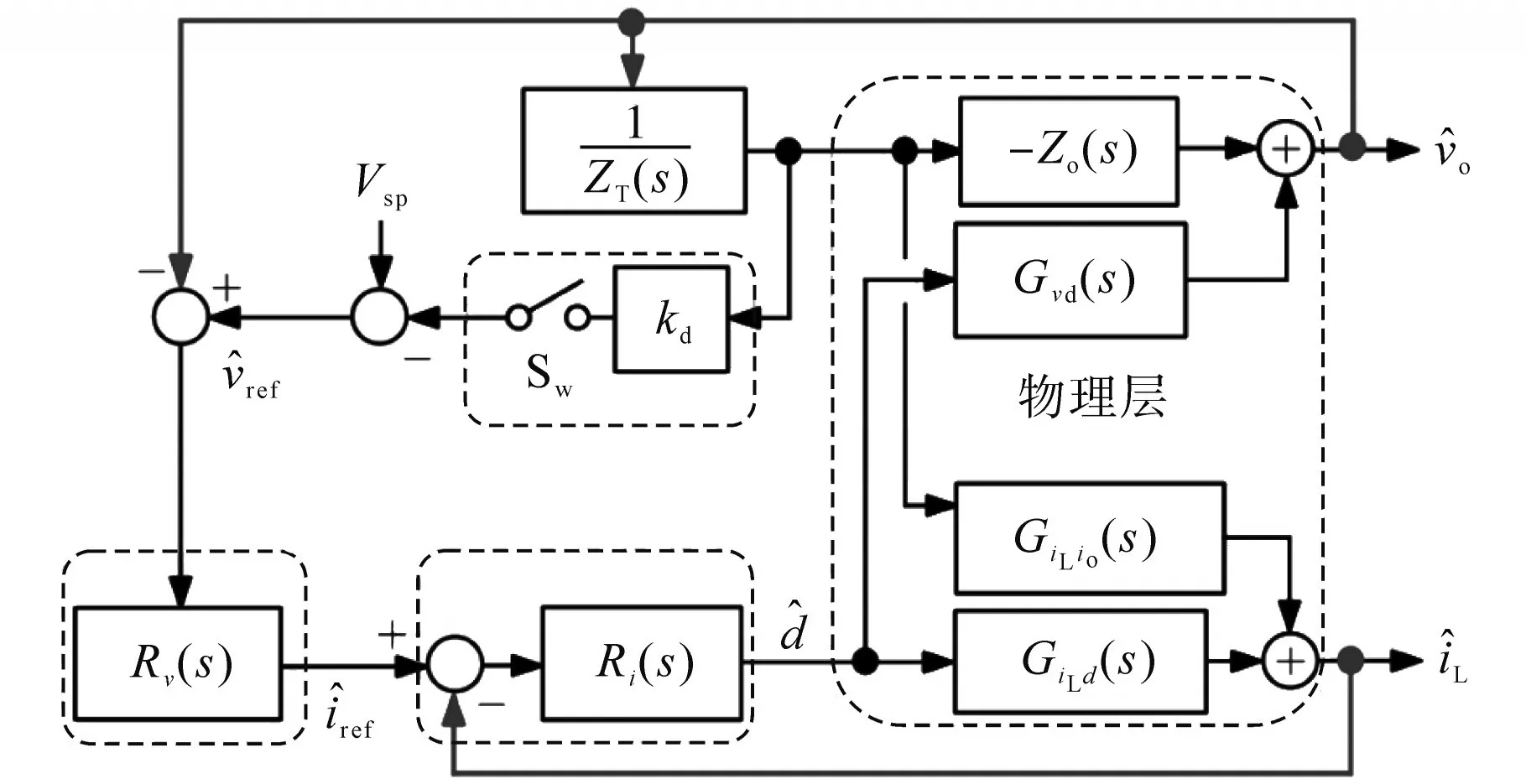
图3 图2中变换器的小信号表示图Fig.3 Small-signal representation of the converter in Fig.2

由图3可知，变流器功率级可以在一个工作点附近线性化：

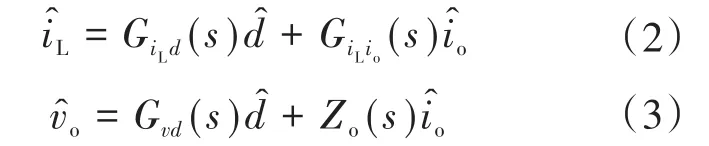
式中：’^‚表示小信号扰动；GiLd(s)，GiLio(s)，Gvd(s)分别为占空比̂与电感电流、输出电流̂ 与̂、占空比̂与输出电压̂的传递函数；Zo(s)为开环输出阻抗。

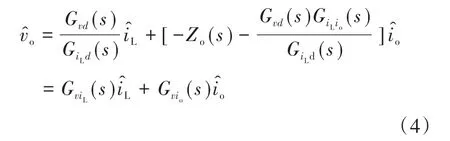
用电感电流和输出电流来表示输出电压，可将图3简化为图4a。由图4a可知，利用叠加理论结合标准块化简技术，在电流环闭合时，输出电流到输出电压的传递函数可表示为电流控制变换器的输出阻抗：

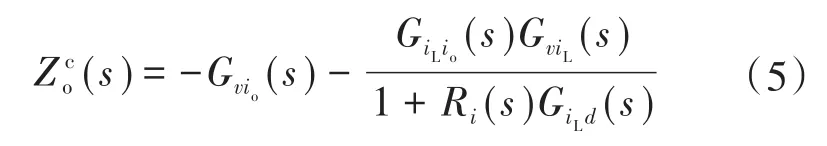
式中负号是由于向外输出电流。同理，无载时电压回路增益为

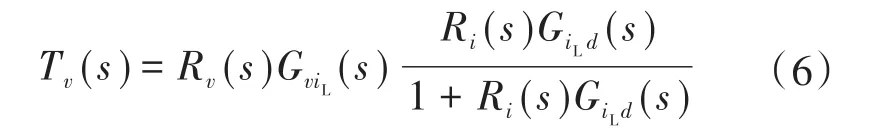
利用式（5）和式（6），在标准块化简技术的基础上，可以将图4a进一步简化为图4b。则电流和电压闭环时输出电流到输出电压的传递函数为

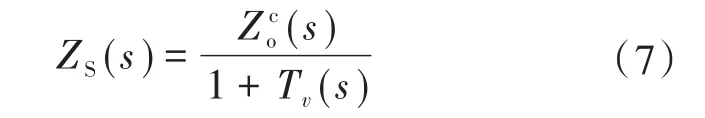
同样根据图4b，考虑负载效应作为反馈项的开路电压回路增益可表示为

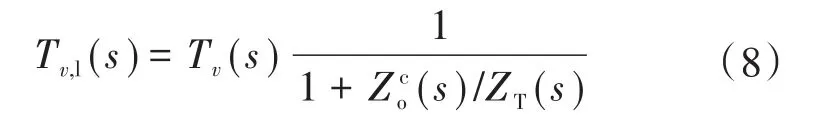
式（7）和式（8）可以通过梅森的规则应用到图4的框图，或运用麦德的额外元素定理考虑ZT的额外元素。结合式（7）和式（8）得到：

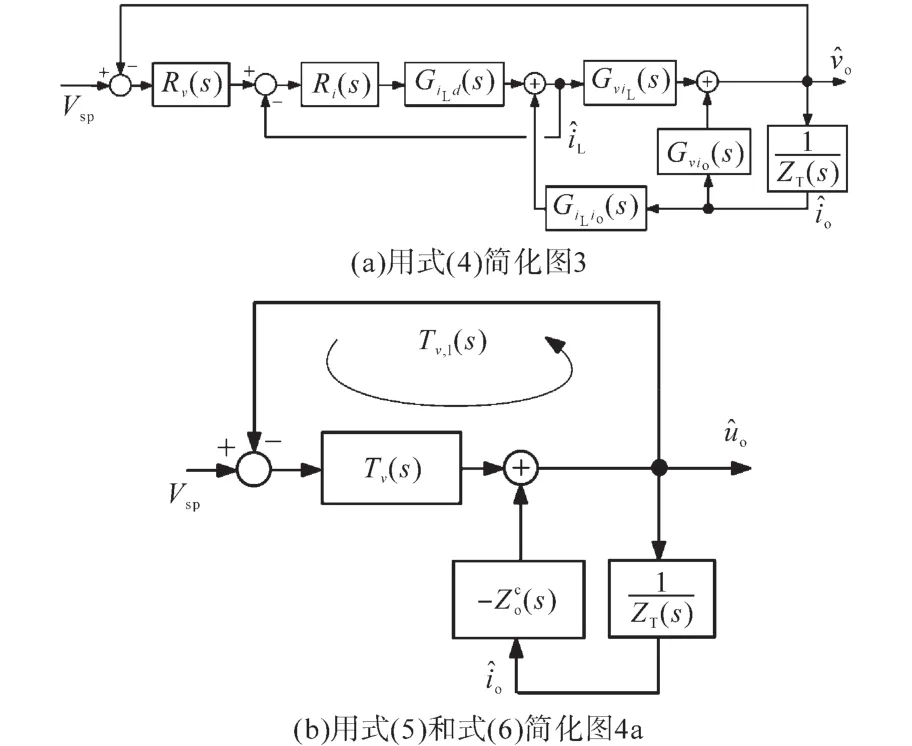
图4 图3的简化表示Fig.4 Simplified representations of Fig.3

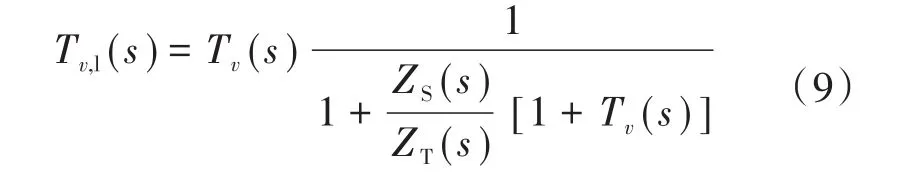
式（9）可表示连接到一定数量的电源和负载转换器的通用DER转换器的环路增益。如果有一个新的源侧变换器连接到直流母线上，式（9）中唯一的变化将是ZT，即之前的值必须与新的源侧变换器的输出阻抗并联。当源侧输出阻抗ZS的大小与负载输入阻抗ZL的大小相当时，就会出现母线阻抗共振。如果ZS(jω)≃ -ZT(jω)，对于某个频率ωo，根据式（9），则Tv,l(jωo)→ -1，这意味着环路增益在ωo超过0 dB，相位裕度近似为0，因此在不稳定的边缘。这就是母线阻抗中较大的谐振峰和较低的相位裕度都是直流微电网不稳定问题的可靠指标。

1.2 母线阻抗建模

结合式（9）和式（1），可以用源侧变换器的电压回路增益表示母线阻抗：

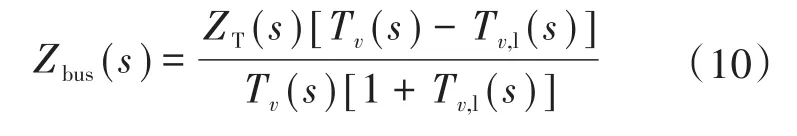
式（10）适用于连接到直流母线的任意数量的电源和负载转换器。

2 母线阻抗的简化估计与调谐

由式（10）可知，要获取母线阻抗，就需要知道母线侧阻抗ZT、环路增益Tv，Tv,l。在实际运用中，这需要进行几次频率响应测量，从而产生问题[19]。为了进行必要的测量，本文进行了一些简化，以提供在其显示主共振的频率（即ωo）附近的母线阻抗的估计。为此，先把式（10）写成极坐标形式：

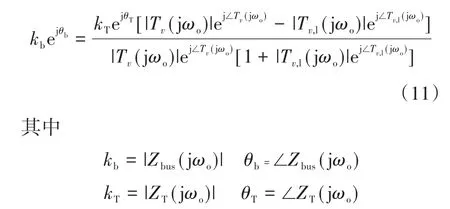
由于Tv(jωo)在设计阶段已经知道，只需要测量ZT(jωo)和 Tv,l(jωo)。为此，第一步是确定母线阻抗共振频率ωo的位置。对于含多电源的微电网，式（11）并不容易简化，首先，母线阻抗可能不再受单峰谐振控制，可能涉及多个谐振；其次，在单源情况下，ωo的位置不易估计。因此，含多电源的微电网的一般情况是较复杂的。因此，首先，所有并行工作的源侧变换器（每个都可以近似为线性时不变系统）在最初设计时都具有良好的相位裕度，以供它们单独运行；其次，源侧变换器的电压环带宽彼此之间距离不太远，这个可以在设计阶段完成，也可以在以后将它们连接到直流总线时完成。基于上述分析，可得：

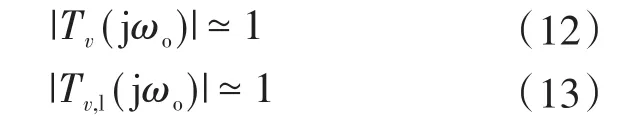
式（12）、式（13）说明母线阻抗谐振出现在变换器的电压环带宽附近。因此，对于多个电源情况，每个源侧变换器所考虑的kT是与其他源侧变换器输出阻抗平行的负载阻抗的大小。通过在上述模拟的互联系统中加入另一个源侧转换器，验证了多源情况下估计公式的准确性。在这种情况下，为了实现电流共享，通过闭合图2中的开关Sw，采用了下垂回路（下垂系数kd=2.6 V/A）。在本次试验中，两种变流器的电流稳压器是相同的。源侧变换器2的电压环带宽固定在f2c=200 Hz，而源侧变换器1的电压环带宽f1c在100～300 Hz变化。这种变化带来了不同的稳定情况，可以通过观察图5a中的相位裕度或图5b中的母线阻抗来获取。

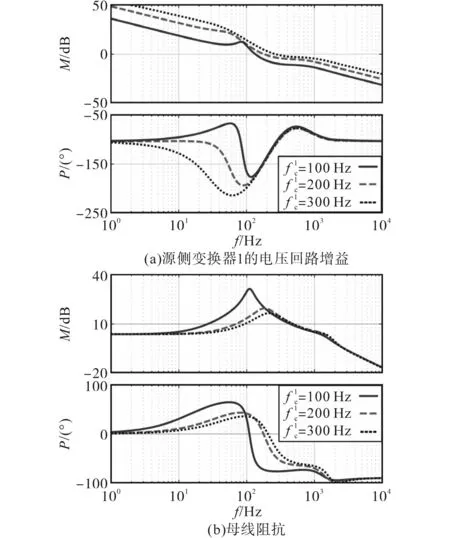
图5 具有两个源侧转换器和一个CPL的系统环路增益和母线阻抗Fig.5 Loop gain and bus impedance of the interconnected system with two source converters and a CPL

针对电压回路的相位裕度ϕm,l，可使用下式来估计母线阻抗kb的峰值：

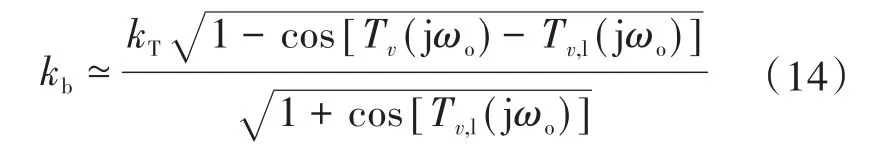
通过在一个控制回路正常运行期间注入一个小信号扰动，比较前、后两个信号的振幅扰动点（vy和vx），基于振幅不同，注入频率调整，直到两个点振幅相等，这就是统一环路增益频率（即交叉频率）：

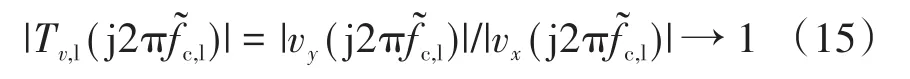
在该频率上，vy和vx之间的相移给出了相位裕度：

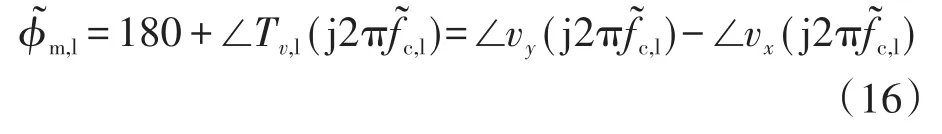
因此，需要对kT进行连续测量，kT可以通过数字控制器内的测量得到，并在注入频率处对输出电流和母线电压进行了采样：

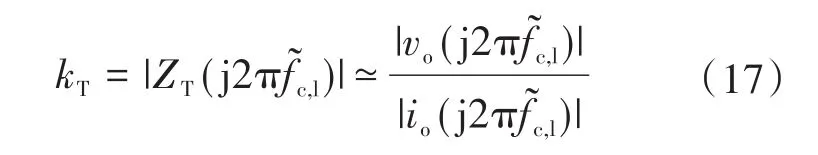
图6为所提监测和调谐技术的示意图，该技术在不中断反馈路径的情况下使用回路注入。

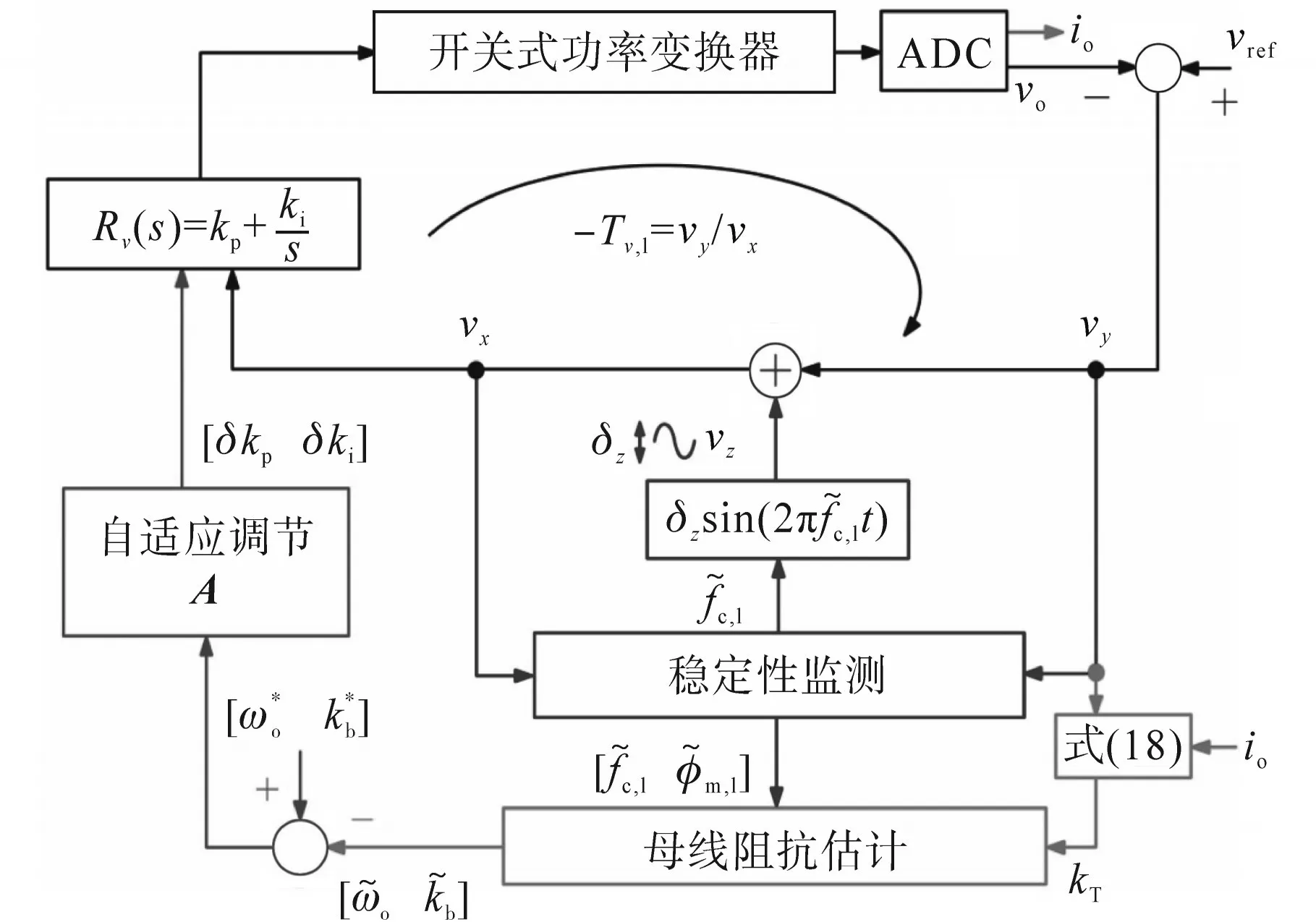
图6 所提在线监测和调谐方法Fig.6 Proposed online monitoring and tuning scheme

图6中，2×2调谐矩阵A是基于外环装置设计的，表示如下：

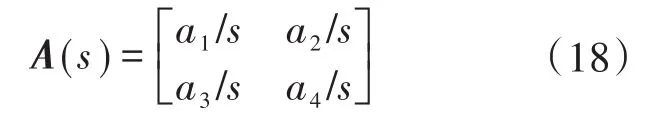
积分增益a1，a2，a3，a4为基于小信号变化的交叉频率和峰值母线阻抗数值选择的，因此，母线阻抗估计和阻尼可以实现，只需注入一个正弦扰动到源侧变换器的电压回路。

3 仿真分析与实验验证

图7为孤岛直流微电网仿真实验结构图。

由图7可知，它由两个Buck转换器组成。源端变换器仿真DER变换器，负载端变换器在源端变换器的带宽范围内充当CPL。仿真实验系统的相关参数如下：输入电压Vin=200 V，母线电压Vbus=100 V，额定功率Pn=1 kW，输出侧电感Lo=1 mH，输出侧电容Co=90 μF，开关频率fsw=20 kHz。

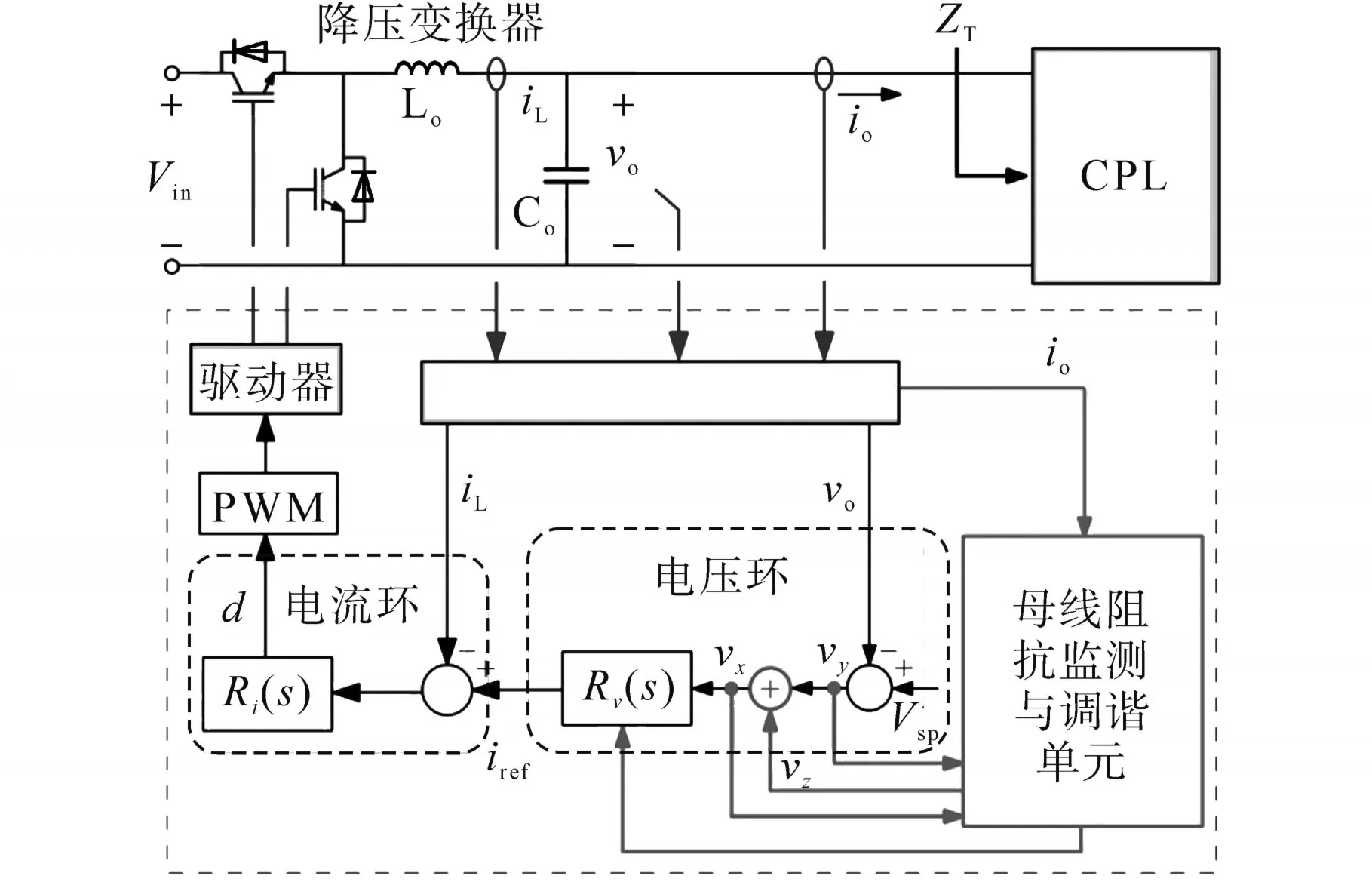
图7 孤岛直流微电网仿真实验结构图Fig.7 The laboratory setup emulating an islanded DC microgrid

图7中提出的母线阻抗监测和调谐工具是在源侧变换器的数字控制器（dSPACE DS1104）中实现的。采样频率被设置为等于开关频率（20 kHz）。源侧变换器控制器包含两个控制回路：电感电流回路和输出电压回路。电流和电压调节器（Ri(s)，Rv(s)）是根据标准程序设计的，用于标称电阻负载。其中，电流环带宽和相位裕度分别为1 kHz和80°，电压环带宽和相位裕度分别为fc=100 Hz和ϕm=55°。但是当连接源侧变换器到CPL时，电压回路的稳定裕度变化明显，而电流回路的稳定裕度基本不变。为了验证所提出的监测和调谐方法，对不同情况下的回路增益和母线阻抗进行了实验测量，并与解析模型进行了比较。为了获得测量值，在变换器的占空比上注入一个小信号伪随机二进制序列，以在较宽的频率范围内对系统进行模拟。然后，通过对输入和输出进行傅里叶变换，并计算它们的比率，就可以得到所需的传递函数。

3.1 调谐前

如上所述，450 W CPL接入会导致电压回路的相位裕度减小（即从55°减小到22°），如图8所示。

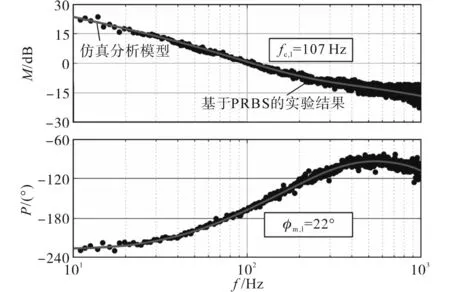
图8 分析和实验测量Tv,l（调谐前）Fig.8 Analytical and experimentally measured Tv，lbefore tuning

根据式（14），此阶段相位裕度估计母线阻抗的峰值约30 dB。为了进一步验证这一估计，对母线阻抗进行了实验测量并绘制在图9中。由图9可知，峰值母线阻抗的实际值（27 dB）接近于估计值。比较图8和图9可得，仿真分析模型与实验测得的频率响应一致，这验证了仿真分析的正确性。

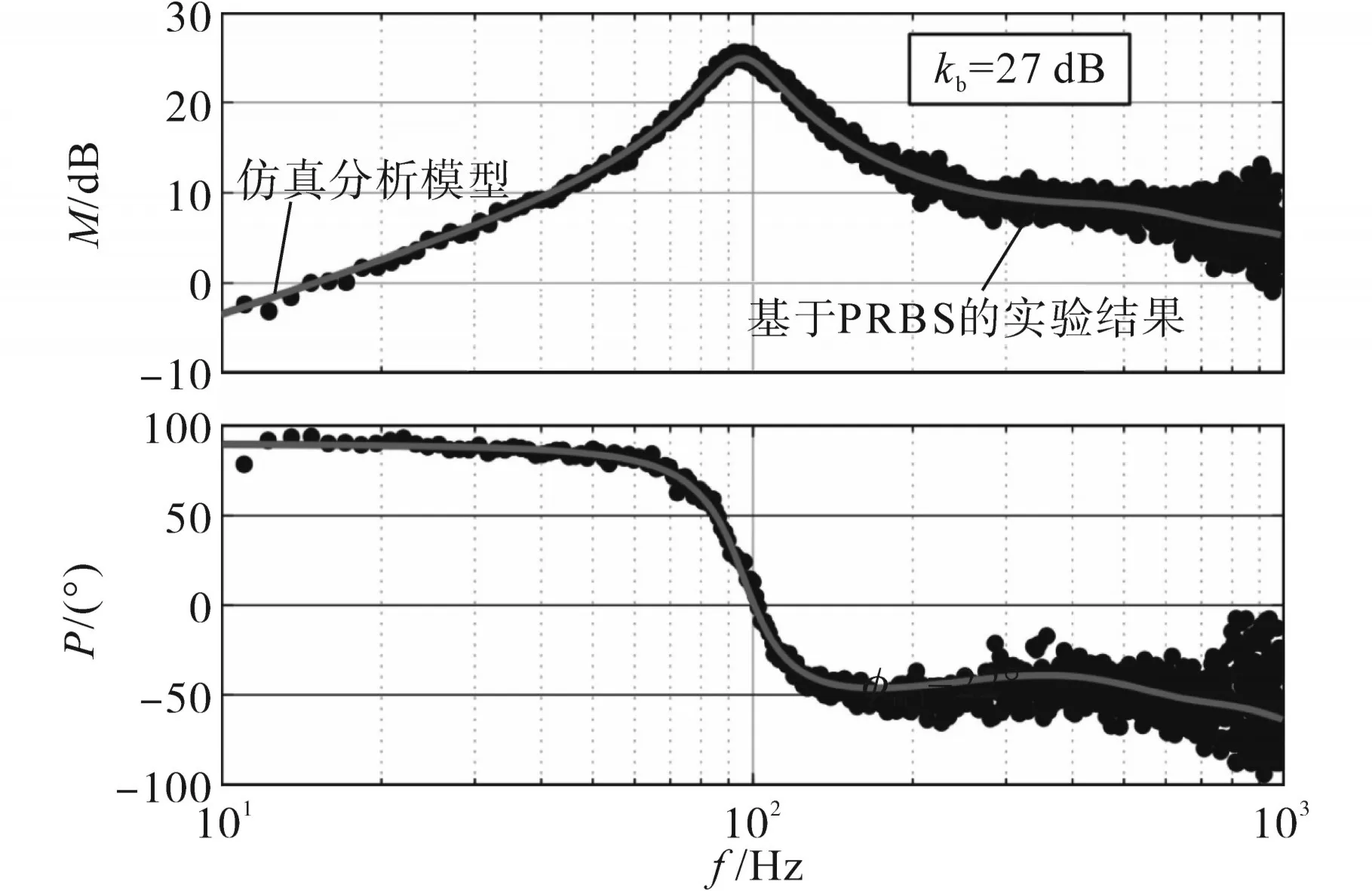
图9 分析和实验测量Zbus（调谐前）Fig.9 Analytical and experimentally measured Zbusbefore tuning

图10为监测的交叉频率、相位裕度和母线峰值阻抗的实验结果。对所提的峰值母线阻抗监测工具在系统暂态状态下的性能进行了评估。特别是CPL功率从450 W降低到225 W时，相位裕度从21°增大到39°，母线峰值阻抗降低。这与式（1）一致，CPL功率越小，破坏稳定性越小。当CPL功率从225 W增加到450 W时，则相反。值得注意的是，在图10中，估计的相位裕度接近于图8中测量的相位裕度，母线阻抗峰值也接近图9中的实测值。在图9中，母线阻抗的相位被限制在[-90°，+90°]区域。同时，母线阻抗没有RHP极点，因此，不违反PBSC。但由于Zbus的谐振较大，使得互连系统的阻尼水平较低。图8中22°的相位裕度也证实了这一点，这与原始的55°相差很大。因此，我们应该调整源侧的电压调节器Gv（s），以阻尼母线阻抗，这也会增加相位裕度。

图10 稳态和暂态下本文所提方法的实验结果Fig.10 Experimental results of the proposed monitoring tool in steady-state and transient

3.2 调谐后

调谐目标是确保母线阻抗在允许的范围内。本文是基于假设母线阻抗的共振频率接近设计电压的带宽环fc。因此，一般情况下，参考交叉频率应保持在原设计带宽附近，即ω∗o≃ 2πfc。本文略微增加参考交叉频率（从100 Hz到125 Hz），以评估电压回路带宽与母线阻抗共振频率（ω∗o≃ 2π× 125rad/s）存在差异时，所提出监控方法的性能。调谐矩阵A是对角线的，al=0.001和a4=0.28。对Gv（s）参数进行调整后，实验测得电压回路的频率响应如图11和图12所示。

图11 分析和实验测量Tv,l（调谐后）Fig.11 Analytical and experimentally measured Tv，lafter tuning

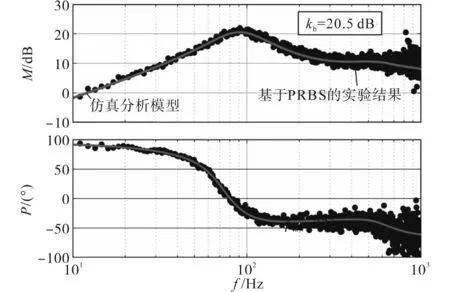
图12 分析和实验测量Zbus（调谐后）Fig.12 Analytical and experimentally measured Zbusafter tuning

由图11可知，电压回路的仿真分析模型是通过应用更新的值ki，kp绘制的，新的相位裕度为40°，证实了动态稳定性得到提高。基于式（14），利用这个值来估计峰值母线阻抗约19 dB。母线阻抗峰值的新值与参考值之间的密切匹配确认了电压调节器的正确调谐，使得母线阻抗达到期望阻尼。在ω∗o≃2π×100rad/s下也进行了类似的实验，与调谐前的情况类似，所实现的监测工具的准确性通过母线阻抗测量进行了验证。将实验得到的母线阻抗频率响应与图12中的解析模型进行比较。可以看出，母线阻抗峰值在20.5 dB左右，这证实了尽管母线阻抗谐振和电压环带宽之间存在差异，但所提监控方法是正确的，此外，通过所提出的调谐方法成功阻尼母线阻抗。

图13为所提方法下的交叉频率、相位裕度和母线峰值阻抗的监测实验结果。可以看出，当调谐开始时，估计的相位裕度增加，峰值母线阻抗相应减少。调谐后的相位裕度监测值接近图11中测量值。母线阻抗峰值也接近图12中的实测值。最后，图14为调谐前、后母线电压阶跃响应。从图14中可以看出，尽管实验室原型的噪声相对较高，但在线监测和调谐方法对该系统的阻尼很好。

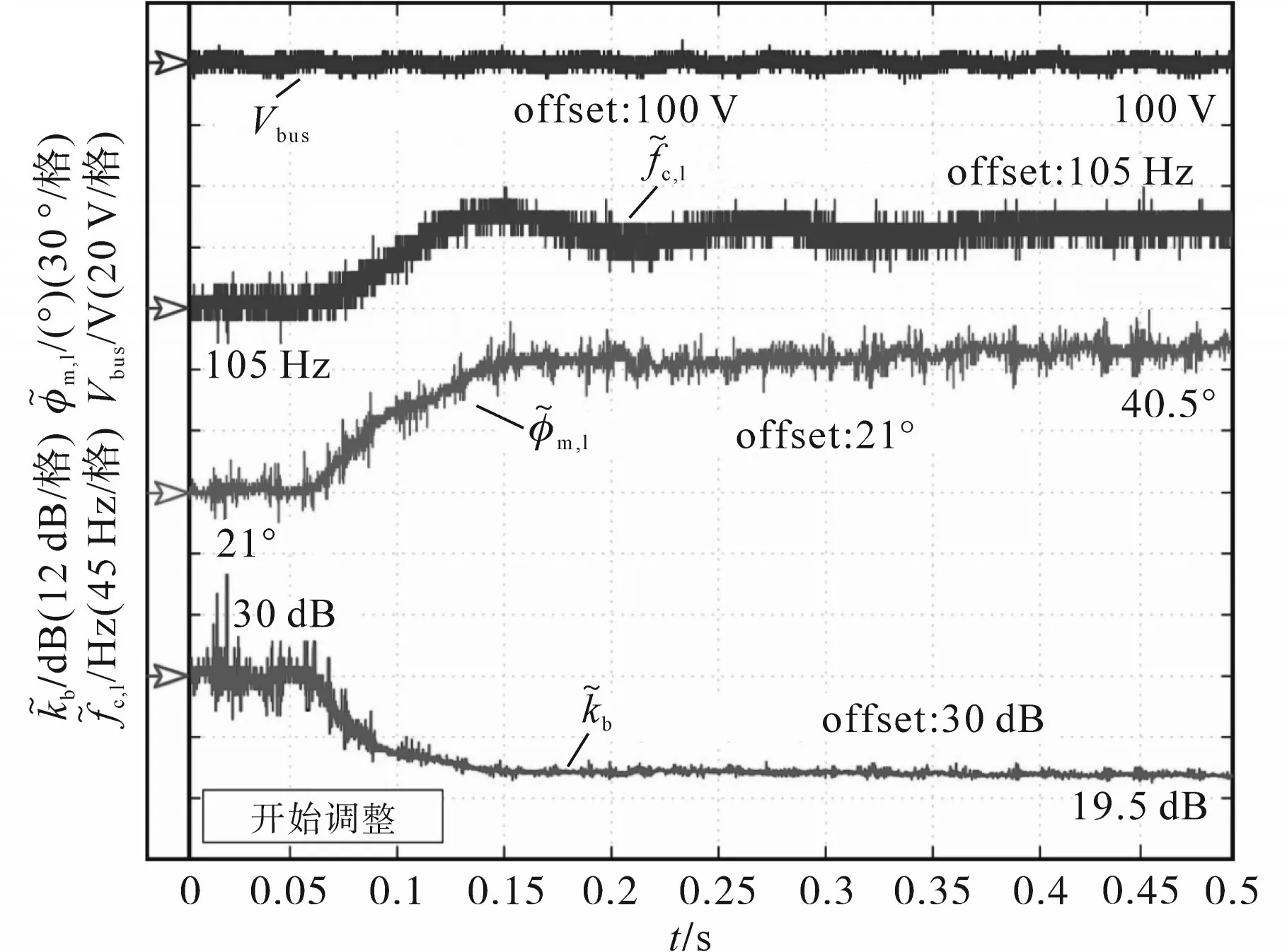
图13 所提监测和调谐单元的实验结果Fig.13 Experimental results of the proposed monitoring and tuning unit

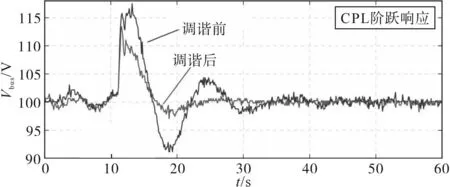
图14 调谐前、后母线电压调节器的电压阶跃响应实验结果Fig.14 Experimental results of the bus voltage step response before and after tuning the voltage regulator

4 结论

直流母线阻抗已被证明是衡量直流微电网稳定性和动态性能的指标。在本文中，母线阻抗用通用直流微电网DER变换器的电压（或下垂）环路增益表示。然后，在连续测量电压回路相位裕度的基础上，推导出一种简化的母线阻抗峰值估计方法。本文借用米德尔布鲁克的注入技术实现在线估计交叉频率和在DER转换器内的通用环路的相位裕度。在预估成功后，通过在线调整稳压器参数来抑制母线峰值阻抗，从而提高直流微电网的动态稳定性。为了验证估计的准确性，对母线阻抗和电压回路增益的频率响应进行了实验测量。实验测量的峰值母线阻抗和相位裕度与在线估计的匹配良好。此外，本文提出的母线阻尼方法消除了阻抗测量的需要，易于在数字控制器内实现，精度高，并且对母线上可能存在的其他频率分量可能产生的噪声和扰动具有鲁棒性。由于本文所提方法是针对单个直流微网设计的，因此，并不适用多直流微网互联场景，故后续将研究直流微网互联时的母线阻抗在线估计和阻尼方法。