基于残差生成器的分散补偿控制策略

周文，杨少波

（国网河北省电力有限公司电力科学研究院，河北 石家庄 050021）

近年来我国的社会经济水平飞速发展，高比例可再生能源伴随着电力电子装置开始大规模地接入到电网系统中[1-2]。直流微电网是可再生能源并网的关键桥梁，其通常由分布式能源、电力电子装置、储能装置、保护装置以及多种类型的负荷组成[3-4]。为了电网技术的发展，实现电力系统的智能化，直流微电网需要得到进一步推广[5]。而提高系统可靠性、解决电能质量问题是直流微电网研究的重点。

维持直流微电网系统稳定运行的关键是保持母线电压的恒定，由于靠近用户侧，受到负载投切的影响，直流母线电压容易发生突变[6]。同时分布式微源的投切和输出功率的随机性同样会造成直流母线电压波动。传统的控制策略可以保证正常情况下的母线电压稳定，但在电能质量问题发生时，母线电压无法维持稳定。

为了解决此问题，众多专家学者进行了相应研究。文献[7]提出了基于储能电池的协调控制策略，保持直流母线电压的稳定。文献[8]基于非线性扰动观测器提出了一种直流母线电压控制方法，增加系统的鲁棒性。文献[9]在文献[8]的基础上改进DC-DC双向变流器控制策略，从而解决了直流母线电压波动的问题。文献[10]基于残差生成器提出了一种新型的直流母线电压控制策略，实现了直流母线电压波动幅值的削弱。文献[11]基于直流分布式电网的弱耦合特点提出了一种基于鲁棒分散式的电压控制框架，抑制了变换器和本地负载接入/切除所产生的电压波动。文献[12]中提出了一种计及直流微电网扰动抑制的残差动态分散补偿控制策略，将本地负荷电流、线路电流稳态值与环流作为扰动进行补偿，但此方法需要添加多个电流信号采集器，增加了系统成本，不利于实际应用。

为保证直流微电网母线电压的稳定，在原变换器采用分散控制的基础上，本文提出了一种基于残差生成器的分散式补偿控制策略。在直流微电网Boost变换器I—V下垂控制基础上，针对负载投切和分布式微源输出功率波动造成的母线电压波动问题，利用模型匹配原理设计求解补偿控制器，通过基于残差生成器的分散式补偿控制策略对直流母线电压波动进行抑制，增强了直流微电网系统的抗干扰能力。

1 系统建模与下垂控制

1.1 Boost变换器建模

Boost变换器是常见的电力电子转换装置，在直流微电网中经常并联应用，并联系统如图1所示。其中，upcc为直流母线电压；Rpcc为公共负载；ipcc为公共负载电流；rline，i，rline，j分别为变换器 i和 j的线路电阻；Ri，Rj分别为变换器i和j的本地负载；Li，Lj分别为变换器i和j的电感；Ci，Cj分别为变换器i和j的电容；ri，rj分别为变换器i和j的电感寄生电阻；iL，i，iL，j分别为变换器 i和 j的电感电流；uc，i，uc，j分别为变换器 i和 j的电容电压；io，i，io，j分别为变换器 i和 j的输出电流；Ei，Ej分别为变换器i和j的稳定直流源电压；iij为变换器 i流向变换器 j的电流；iload，i，iload，j分别为变换器 i和 j的本地负载电流；ipcc，i，ipcc，j分别为流向Boost变换器i的公共负载电流。

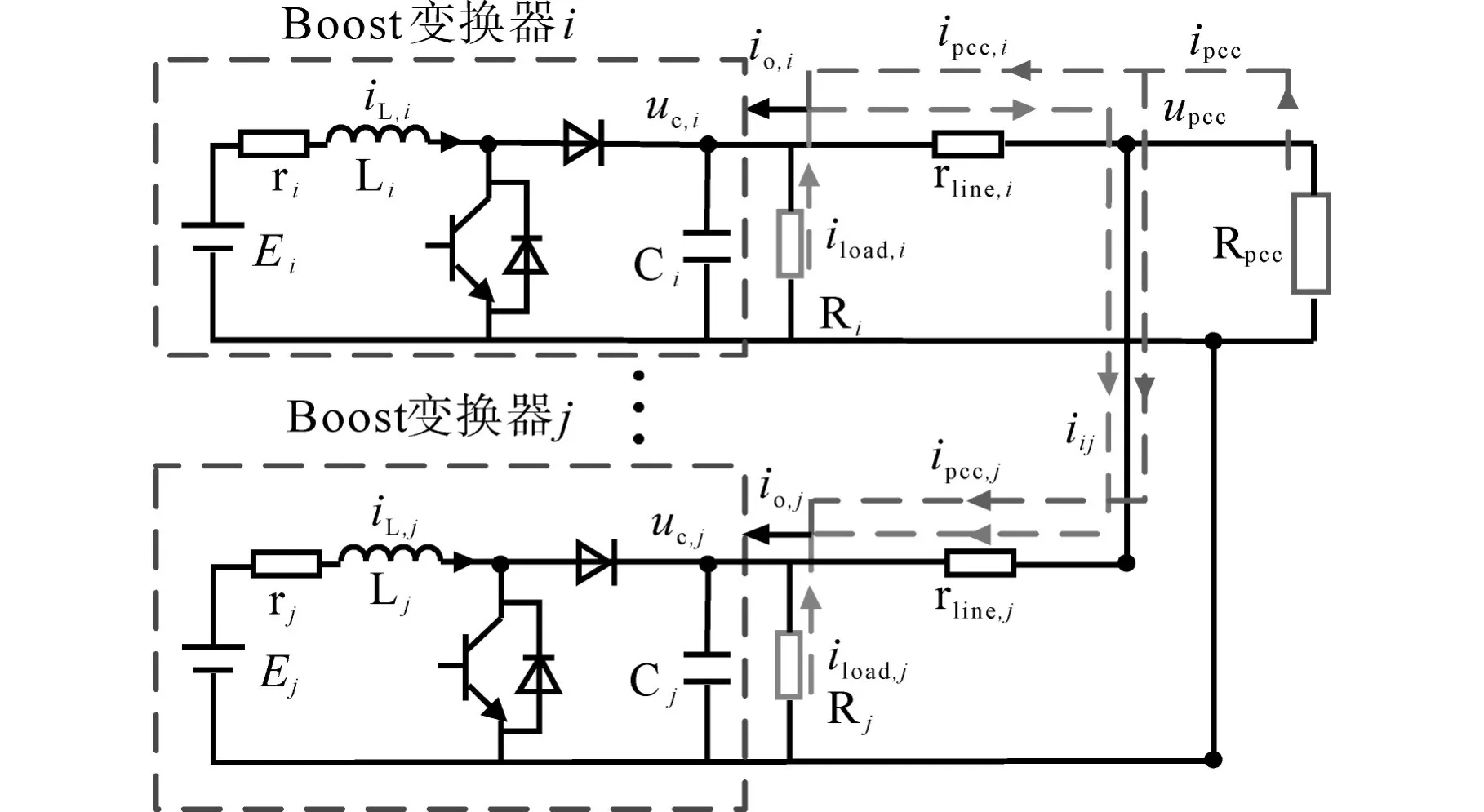
图1 Boost变换器并联系统Fig.1 Boost converter parallel system

根据图1得到Boost变换器i的微分方程为

式中：Di为Boost变换器i的开关占空比。

在考虑本地负载电流、公共负载电流和变换器之间电流的基础上，Boost变换器i的输出电流可表示为

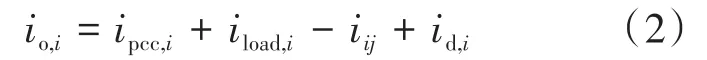
式中：id，i为变换器i的非基波扰动电流，其在理想状态下为0。

在式（1）中存在（1-Di）uc，i和（1-Di）iL，i两项非线性项，为得到Boost变换器的状态空间模型，定义稳定点的微分方程如下：

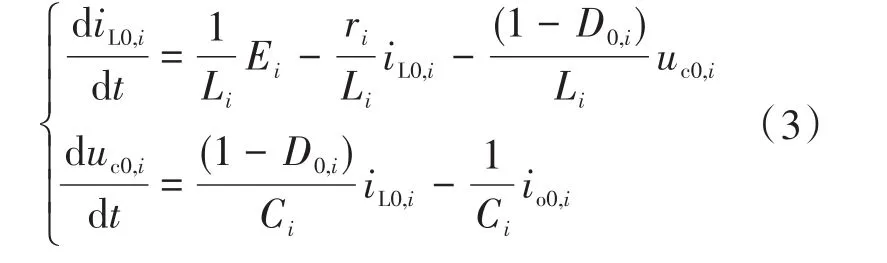
式中：D0，i为变换器 i的稳态点占空比；uc0，i，iL0，i分别为变换器i的稳态点电容电压和电感电流；io0，i为变换器i稳定点输出电流，其不包含扰动电流项 id，i。

当变换器为单极调制，载波幅值为1时，调制波uk，i=Di。结合式（1）和式（3）得到稳定点处的线性化状态空间方程：

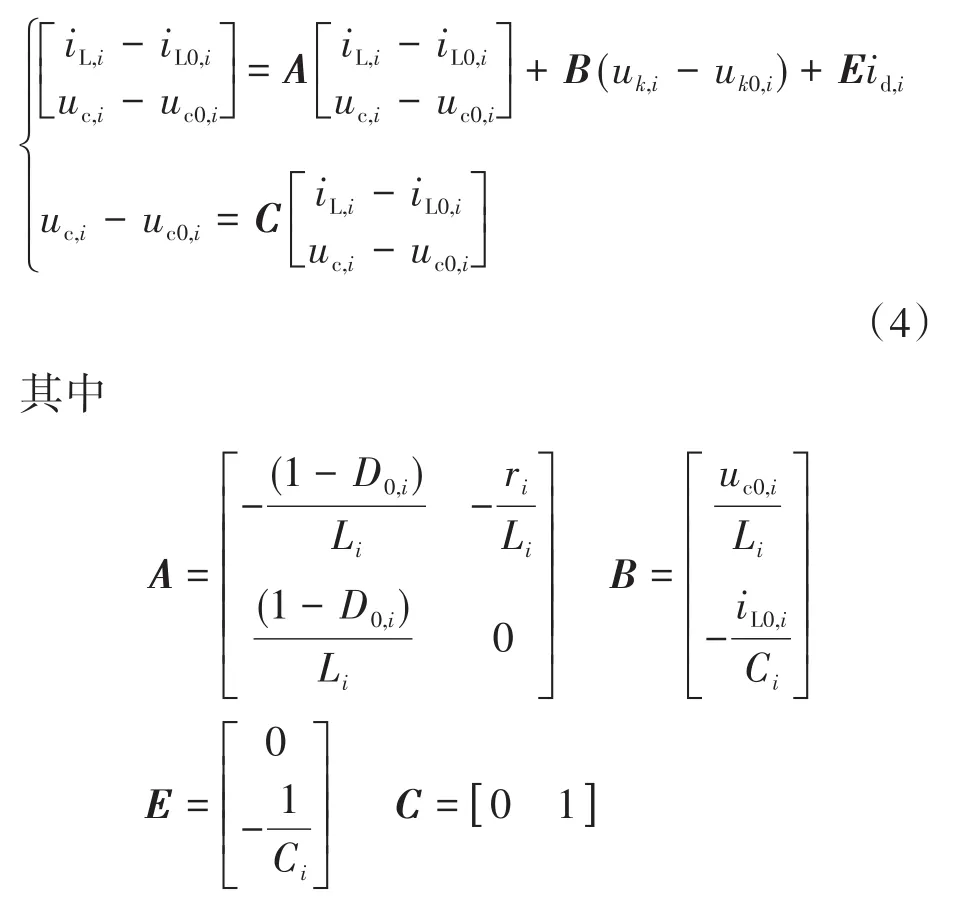
1.2 直流下垂控制与电压偏差补偿

为使变换器实现分散控制策略，完成负载电流均分，本文并联Boost变换器采用基于I—V特性曲线的下垂控制策略，其控制策略表达式为

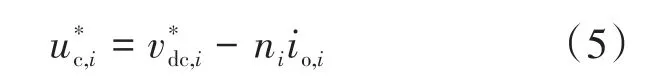
在采用I—V特性曲线情况下，两台变换器输出电流的关系为

式中：nj为Boost变换器j的下垂系数，也可称为虚拟电阻。

在传统的下垂控制中，虽然可以根据下垂系数对变换器输出电流按比例控制，但是下垂系数同时导致了输出电压的偏差，进而影响到母线电压的稳定性，因此需要设计电压偏差补偿控制，从而实现母线电压稳定，其表达式为[13]

2 分散式补偿控制结构

2.1 基于残差生成器的分散式补偿控制结构

根据式（4）得到系统的一般状态空间表达式为

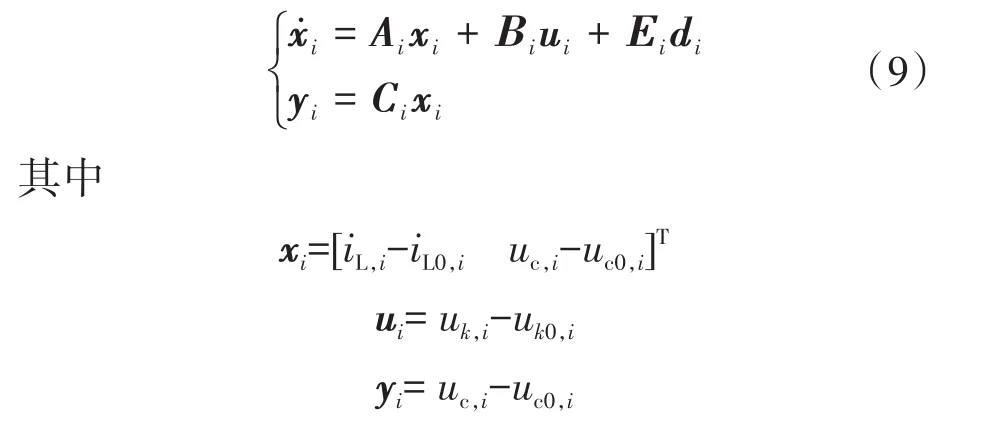
式中：xi为变换器i的状态量；ui为变换器i的输入量；di为变换器i的扰动输入量；yi为变换器i输出量；Ai，Bi，Ci，Ei为适当维数矩阵。

根据式（9）被控对象状态空间模型，采用极点配置设计观测器增益矩阵Li，从而得到状态观测器的状态空间方程：

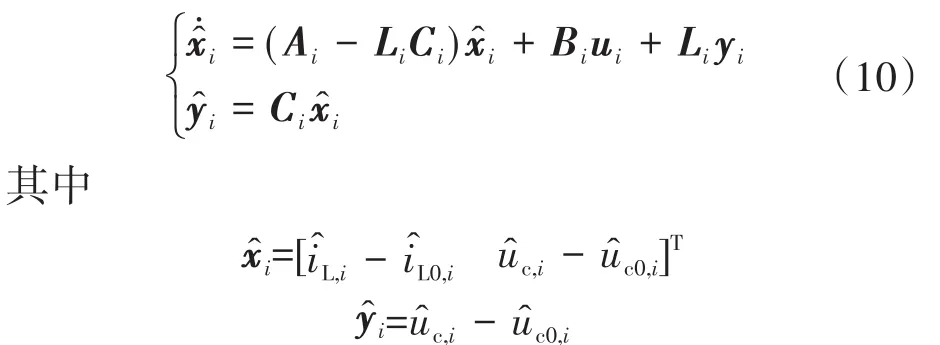
基于下垂控制的Boost变换器并联系统是典型的分散控制结构，在原控制器保证系统稳定时，针对扰动输入对系统稳定性的影响，文献[14]中提出了一种基于残差生成器的容错控制结构，如图2所示。

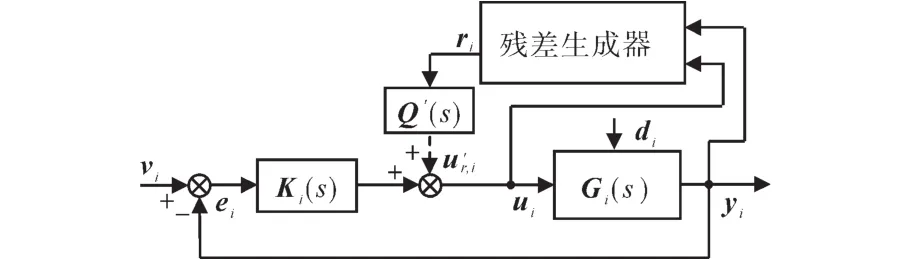
图2 基于残差生成器的补偿控制结构Fig.2 Compensation control structure based on the residual generator

在图2中，残差信息ri常被用来进行系统故障定位与诊断，以及扰动的检测与抑制。为得到系统的残差，根据式（9）和式（10）得到残差生成器的状态空间表达式为

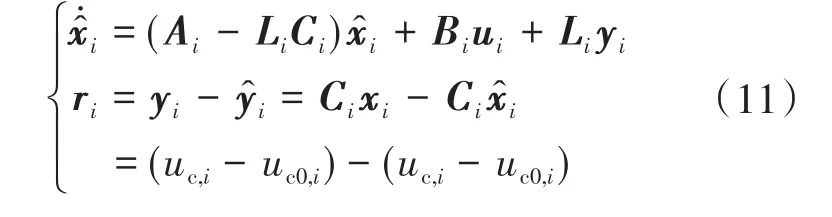
式中：ri为残差输出量。

残差信息能体现扰动和故障等因素对系统的影响程度，当系统不受扰动和故障影响时，ri=0；当系统受到扰动和故障影响时，ri≠0。

如图3所示，在Boost变换器采用下垂控制策略时，补偿控制器Q′（s）的补偿控制信号u'r,i对扰动di进行补偿，从而保证输出信号yi的稳定。然而，通过下垂控制中的电压电流双闭环结构会导致二次扰动的出现。u'r,i经过部分被控对象G1，i（s）后会通过反馈通道影响电流内环误差e1，i，造成二次扰动。为了避免补偿信号变为新的扰动信号，将补偿控制器Q′（s）进行位置变化，得到新的控制结构，其补偿控制器为Q（s）。

图3 基于残差生成器的改进补偿控制结构Fig.3 Improved compensation control structure based on the residual generator

2.2 补偿控制器求解

为方便采用模型匹配的方法求解补偿控制器Q（s），对图3中的控制结构进行转换，由式（9）和式（10）得到扰动残差生成器的状态空间表达式为

式中：xrd为状态量；drd为输入量；yrd为残差输出量。

基于式（12）可将图3中以控制信号ui和输出信号yi为输入的残差生成器转化为以扰动信号di为输入的扰动残差生成器，如图4所示。

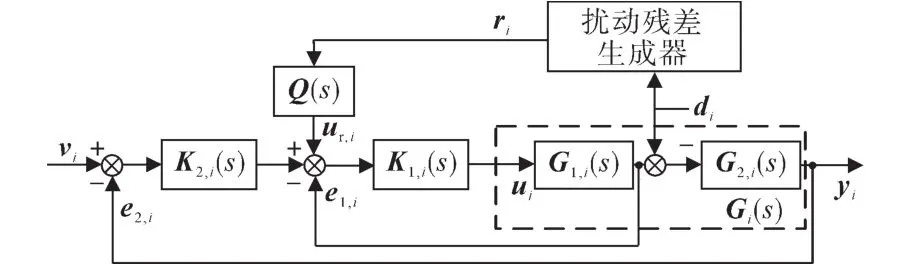
图4 基于扰动残差生成器的改进补偿控制结构Fig.4 Improved compensation control structure based on the disturbance residual generator

根据图4在没有给定输入的情况下，只考虑扰动信号di为系统输入时，得到系统的模型匹配结构，如图5所示。

图5 模型匹配结构Fig.5 Model matching structure

其中，Trd（s）为以扰动为输入残差为输出的扰动残差生成器，其状态空间表达式为式（11）。Tyd（s）为以扰动为输入的被控对象，其传递函数表达式为

Tp（s）为以补偿信号为输入的被控对象，其传递函数表达式为

根据图5模型匹配结构，在扰动di作为输入时，由于补偿控制器Q（s）的加入补偿了扰动信号di，使得输出zi趋近于0，消除了扰动对系统稳定的影响。Q（s）可通过下式进行求解[15]：

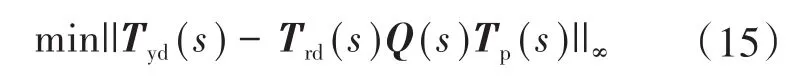
根据图5可以将模型匹配问题转化为鲁棒控制问题，如图6所示。其中，Trd（s），Tyd（s）和Tp（s）构成广义控制对象，Q（s）相当于鲁棒控制器，整个结构属于典型的鲁棒反馈控制结构。由文献[16]可知，Q（s）可采用线性矩阵不等式方法进行求解。

图6 鲁棒控制框架Fig.6 Robust control framework

为了方便在实际工程中的应用，也可用简便方法求解Q（s）。假设在理想情况下zi=0，根据式（15），将Trd（s）的状态空间表达转换为传递函数，得到Q（s）的求解公式为

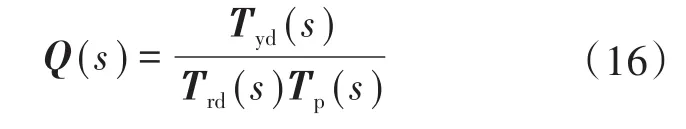
将基于残差生成器的动态补偿控制应用于Boost变换器系统中，得到如图7所示的整体控制结构。

图7 基于残差生成器的Boost变换器并联系统补偿控制Fig.7 Compensation control of parallel system of Boost converter based on residual generator

3 仿真实验

在PSCAD/EMTDC中搭建Boost变换器并联系统，设计公共负载投切和功率波动实验。在同时具有下垂控制和电压偏差补偿控制时，对比有无本文所提补偿控制的电压波形，验证控制算法的有效性。系统参数如表1所示。

表1 Boost变流器参数Tab.1 Boost converter parameters

3.1 公共负载投切实验

在并联Boost变换器并联系统中，直流母线上接入10 Ω负载作为系统的稳态负荷，同时使用20 Ω负载作为投切负荷。在负荷投切时，对比本文所提控制策略与传统直流下垂控制下的Boost变换器输出电压和母线电压，实验结果如图8～图10所示。

图8 无补偿控制时双Boost变换器输出电压（1）Fig.8 Double Boost converter output voltage（1）without compensation control

如图8所示，在公共负载投切时，距离公共负载较远的Boost变换器1输出电压突变幅值较小，减载时突增16.5 V，加载时突降15.2 V。距离公共负载较近的Boost变换器2输出电压突变幅值较大，减载时突增19.1 V，加载时突降18.3 V。

如图9所示，在加入本文所提补偿策略后，变换器输出电压突变幅值明显下降，距离公共负载较远的Boost变换器1输出电压减载时突增0.5 V，加载时突降0.8 V。距离公共负载较近的Boost变换器2输出电压减载时突增1.5 V，加载时突降3.2 V。

图9 补偿控制时双Boost变换器输出电压（1）Fig.9 Double Boost converter output voltage（1）with compensation control

如图10所示，在公共负载投切时，无补偿控制的母线电压突变幅值较大，减载时突增21.6 V，加载时突降19.2 V。在加入本文所提补偿策略后母线电压突变幅值明显降低，减载时突增4.3 V，加载时突降4.1 V，电压变化率分别为1.075%和1.025%，符合5%以内的国家标准。

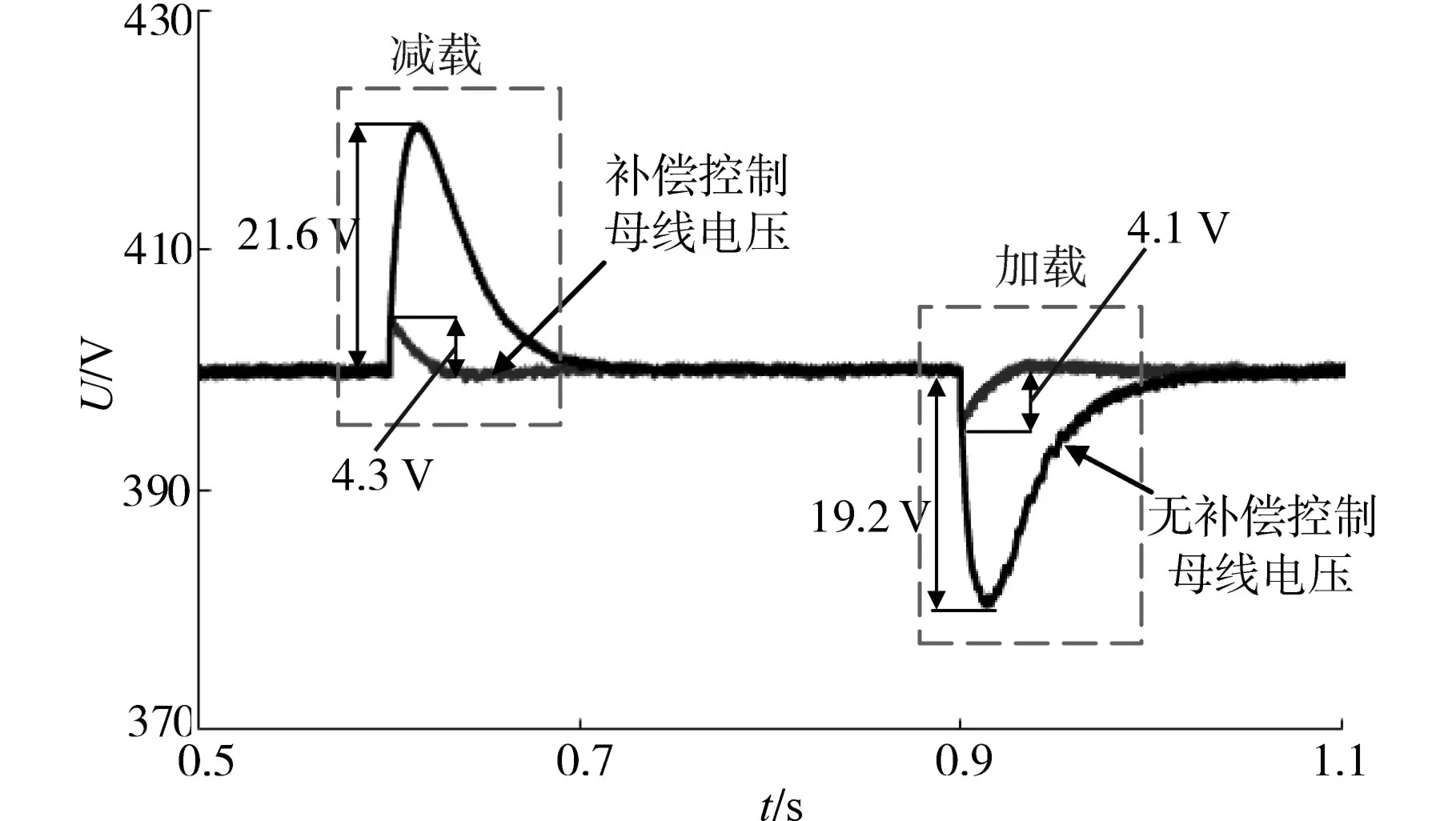
图10 公共负载投切直流母线电压对比Fig.10 DC bus voltage comparison for public load switching

3.2 功率波动实验

在并联Boost变换器并联系统中，直流母线上接入10 Ω负载作为系统的稳态负荷，同时在直流母线上并联受控直流源。通过受控电流源输出正弦电流，模拟分布式微源功率波动，本文所提控制策略与传统直流下垂控制下的Boost变换器输出电压和母线电压，实验结果如图11～图13所示。

图11 无补偿控制时双Boost变换器输出电压（2）Fig.11 Double Boost converter output voltage（2）without compensation control

如图11所示，在功率波动时，距离较远的Boost变换器1输出电压波动幅值差较小，为26.8 V。距离较近的Boost变换器2输出电压波动幅值差较大，为28.8 V。

如图12所示，在加入本文所提补偿策略后，变换器输出电压波动幅值差明显下降，距离较远的Boost变换器1输出电压波动幅值差为8.7 V。距离较近的Boost变换器2输出电压波动幅值差为6.4 V。

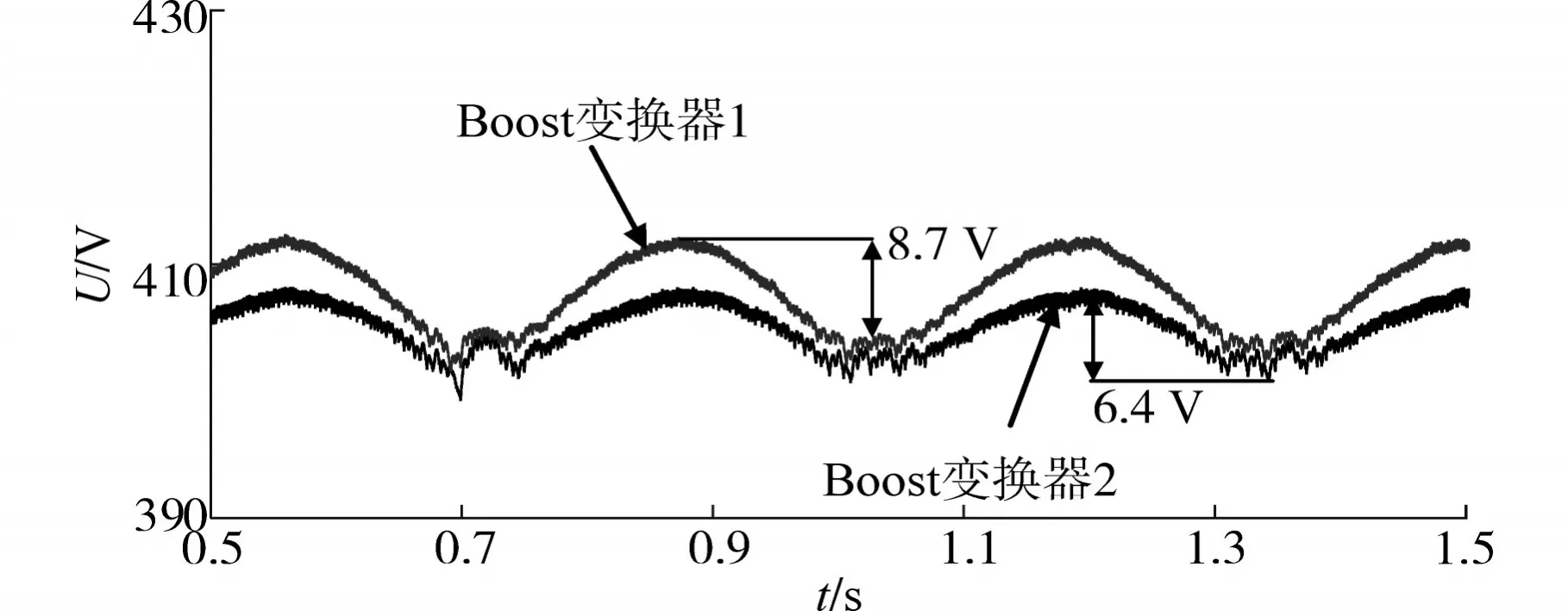
图12 补偿控制时双Boost变换器输出电压（2）Fig.12 Double Boost converter output voltage（2）with compensation control

如图13所示，在功率波动时，无补偿控制的母线电压波动较大，波动幅值差为34.4 V。在加入本文所提补偿策略后母线电压波动明显减弱，波动幅值差为4.5 V，电压变化率为1.125%，符合5%以内的国家标准。

图13 功率波动直流母线电压对比Fig.13 Power fluctuation DC bus voltage contrast

4 结论

本文针对直流微电网中负载投切和功率波动导致的母线电压失稳，提出了一种基于残差生成器的补偿控制结构。以Boost变换器的线性化模型为例，在I—V下垂控制与电压偏差补偿控制的基础上，设计残差生成器与补偿控制器，利用残差信号补偿电流扰动带来的母线电压波动问题，最后在PSCAD/EMTDC仿真平台上，验证了本文所提控制策略的有效性。