基于排列熵及PSOBP的混合配电网故障诊断*
2023-01-06齐沛锋丁煜飞夏寅宇汪缪凡
齐沛锋 韩 笑 丁煜飞 夏寅宇 汪缪凡
(南京工程学院 南京 211167)
1 引言
随着配电网网络结构变得越来越复杂,准确的识别故障类型并及时切除故障对于电力系统稳定性和可靠性有重要影响。城市的发展使得配电网络的结构也越来越复杂,为了减少占地面积,电缆线路被更多应用在城镇的配电系统中,由此形成了架空线-电缆线路混合的配电网络,这种线路由于连接点波阻抗不一致,行波会在连接点、线路末端进行多次的折反射,给继电保护系统带来了挑战。
目前常用的故障类型识别的方法多是基于工频量和暂态量,然后适用信号处理的方法提取特征向量。文献[1]用小波变换分解电压信号,计算电压信号的小波奇异熵,并结合改进的免疫网络进行故障分类。暂态量故障处理方法是先对采集的信号进行处理,进而对故障类型进行判别,可以免受工频因素的影响。文献[2]使用经验模态分解算法从暂态分量电流中提取直流电流,没有充分提取信号的特征。文献[3]使用小波工具箱对三相电流信号进行处理,分析暂态信号的变化特性来判定不同故障类型的故障相。但小波变换只是对固定频率的信号的进行处理,不能完整地反映信号的特性,而且小波基的选择不具有一定的标准,因此结果准确率不能够完全保证。排列熵是一种信号处理的常用方式,可以有效反映时间信号的复杂程度,已经广泛应用在机械故障诊断等领域[4~7],十分适合应用于故障发生后故障相的信号复杂度分析。
随着科学技术的不断发展,越来越多深度算法出现在了故障判别领域,其主要是先建立故障位置和某种故障参数的非线性关系,将多次测量的故障参数组成数据样本,在人工智能模型中进行训练和寻优,直到确定故障的位置。文献[8]使用故障录波器数据中的各类数据,构建故障判别体系,并在数据挖掘过程种使用粗神经网络进行大数据的分析,确定出线路的故障类型。文献[9]使用向量积对高压直流系统故障类型分类,能够准确识别6种故障类型,但是识别故障类型不够完整。文献[10]将故障电压信号经过EMD(经验模态分解)得到的矩阵输入到LS-SVM分类器中,但经验模态分解具有一定的端点效应和模态重叠,会对结果有一定的影响。文献[11]应用在三端直流输电网络中,将采集到的电压故障行波信号进行小波包分解得到不同频段的小波包能量作为样本参数,通过BP神经网络进行非线性拟合,经过多次迭代训练输出故障位置。文献[12]通过推到电压行波的衰减特性,得到线模电压和0模电压的模极大值和故障位置的关系,把不同小波尺度下的模量比值组成特征向量,解决了现有故障测距方法对行波波头难以检测的问题。
针对原来故障定位方案不适应架空线-电缆混合线路的问题,提出了一种数字信号处理和深度学习算法相结合的新型混合线路故障定位方法。先求取故障发生后一个周期内三相电压信号的排列熵的值,将训练集样本输入到模拟退火算法优化后的BP神经网络中,实现对故障相的精确识别。
2 新型配电系统故障分析及特征量提取
2.1 新型配电网系统结构
研究的电缆-架空线混合配电网系统模型如图1所示。额定频率50Hz,左侧为架空线路L1长度为50km,右侧为电缆线路L2长度为10km。在0.2s时,分别在距离左侧电源10km、20km、30km和40km处设置10种故障,持续时间为0.05s,采样频率为10kHz,每种故障设置不同的过渡电阻,过渡电阻为10Ω~100Ω。

图1 混合配电网短路故障示意图
2.2 故障特征的分析
单相接地故障时,故障相的电压明显降低,正常相电压有较小幅度的下降;相间故障时,故障的两相电压下降十分明显且下降一致,非故障相电压略微下降;三相故障时,电压均有很大程度的下降;两相接地故障时,故障相电压下降十分明显,非故障相电压基本不变。在左侧电源信号接收处采集故障发生后一段时间内的三相电压信号,并对其进行分析。
3 算法原理
3.1 排列熵
排列熵算法适用于一维信号的分析,可以为一维信号划分成信号矩阵,对分析突变信号和提取微弱信号有很好的效果,在机械震动故障识别领域已经有广泛的应用。对于暂态故障信号的突变特征,可用排列熵算法进行识别。
3.2 BP神经网络
BP神经网络主要分为三层网络和两条传播路径。BP神经网络的关键在于它会根据输出的结果和真实值的偏差,经过隐含层到输入层,不断更新各层的偏差的阈值,经过不断迭代后,使得误差限定在一定范围内,该网络的故障识别准确率较高,已经被大量应用在各个故障识别的领域中[13~15]。
3.3 模拟退火算法
模拟退火算法作为一种效果很好的随机搜索的算法,已经广泛被应用在图像识别和神经网络中[16~21]。它可以在参数寻优过程中,在一定的概率上找到准确率更高的解,可以提高模型的准确率。
4 线缆混合线路故障判别方法
线缆混合线路故障判别流程如图2所示,首先在混合线路的一端采集三相电压信号,然后共设置10种故障状态,每种故障状态有40组故障样本,每组故障样本分别求取其A,B,C三相电压在发生故障后一个周期内的排列熵,研究在不同的故障位置和过渡电阻的情况下,故障相和非故障相排列熵值的差别,说明该特征向量的可靠性。再从得到特征向量中随机抽取380组数据作为训练样本,其余的20组作为测试样本集。将训练样本输入到参数优化后的BP网络中进行训练,并验证该模型的可行性。
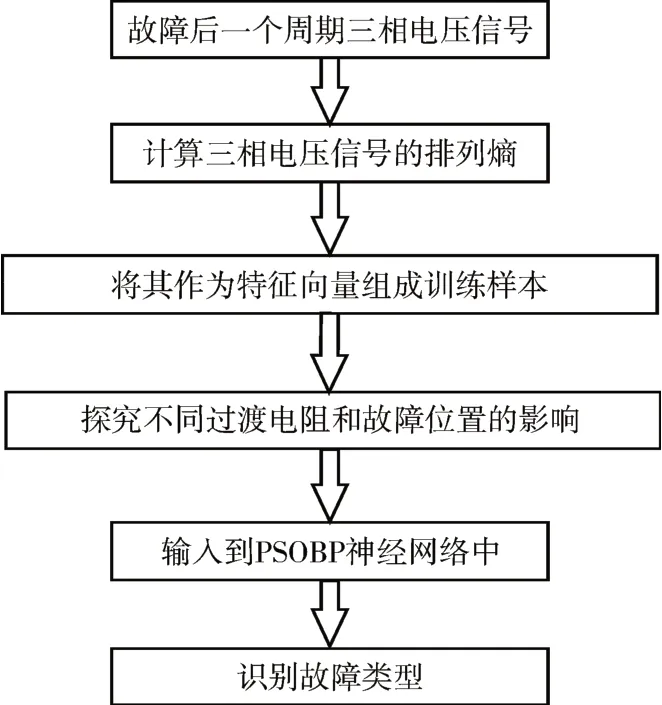
图2 线缆混合线路故障判别流程图
5 算法验证
5.1 建立故障类型识别系统
前面所述,通过仿真得到以下数据集,共400组,其中随机抽取380组数据作为数据样本,剩余20组数据作为测试样本。其中故障点位置分别设置在距离左侧电源10km~40km范围内,为探究过渡电阻对故障类型判别的影响,过渡电阻范围设置为10Ω~100Ω,以10Ω的层级递增。故障类型设置为两相短路、两相接地短路、单相接地和三相短路共10种故障类型,见表1。
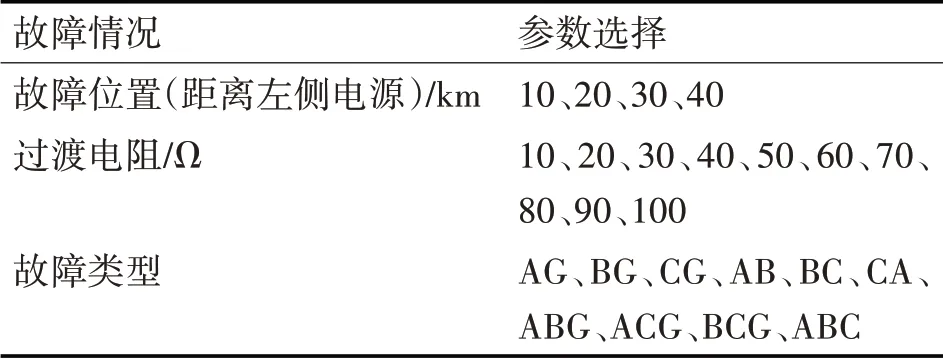
表1 训练样本参数取值
5.2 数据分析
5.2.1 不同故障位置对故障选相的影响
将相同过渡电阻,不同故障位置的数据样本输入到PSOBP模型中,取故障电阻为50Ω,故障位置为距离左侧电源从10km~40km,数据样本是故障发生后三相电压数据。下面对四种故障类型的数据进行分析,样本数据见表2。
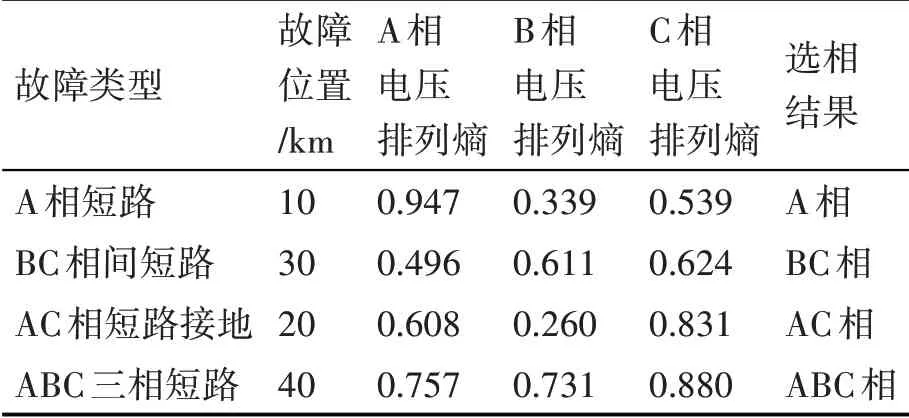
表2 不同故障位置对故障相识别的结果
通过上表可以明显看出,发生故障相的数据的排列熵值更大,故障发生在不同的位置时,故障相的排列熵一般在0.8~0.9,非故障相的排列熵一般在0.3~0.6的范围内,而排列熵是用来衡量时间序列的复杂度,也说明故障相的电压数据更加复杂。
5.2.2 不同过渡电阻对故障选相的影响
将相同故障位置,不同过渡电阻的样本输入到PSOBP模型中,取故障位置为距左侧电源10km,过渡电阻取值范围为10Ω~100Ω之间,数据样本是故障发生后一个周期内的三相电压数据。下面对四种故障类型的数据进行分析,样本数据见表3。
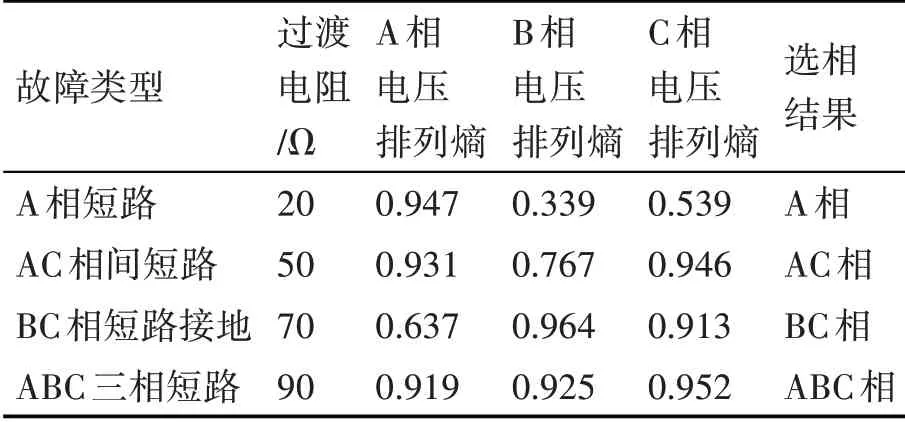
表3 不同过渡电阻对故障相识别的结果
从上面可以看出,发生在不同的过渡电阻时,尤其是在高阻抗发生三相接地的情况最为严重,此时三相的排列熵值都很大,可以反映信号的复杂程度。从表中还可以看出,故障相的排列熵的值都比较大,在0.9以上,非故障相的排列熵的值在0.4~0.7之间。
从以上两种情况,非故障相排列熵值一般在0.3~0.7之间,故障相排列熵一般在0.8~1之间,正常情况下排列熵值为0.441,介于非故障相排列熵值之间,可以看出在不同故障位置和不同过渡电阻的情况下,故障相和非故障相的差别。
5.2.3 PSO优化后的BP网络及算法比较
优化后的BP神经网络适应度函数如图3所示,将测试样本输入到优化后的神经为网络结果如图4所示。为验证该方法的准确性,将排列熵的值分别输入到BP神经网络,决策树和随机森林网络中,比较其识别故障的准确性;另外将故障分量能量系数输入到PSOBP神经网络中,通过表4中的准确率比较可知,在输入特征向量均为排列熵的情况下,PSOBP神经网络的准确率比决策树,BP神经网络和随机森林都要高;当输入特征向量分别为排列熵和能量分量系数时,但都经过PSOBP神经网络中,排列熵和PSOBP神经网络的组合要比能量分量系数的组合准确率高出4%,其准确率识别结果见表4。

图3 适应度曲线图
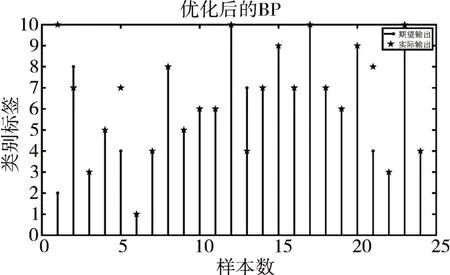
图4 PSO-BP分类结果

表4 不同算法的识别准确率比较
6 结语
提出了一种排列熵和BSOBP神经网络相结合的混合线路故障诊断新方法,以三相电压信号的排列熵作为输入样本,在不同过渡电阻和故障位置下的情况下,可以精准实现对故障的诊断。经过模拟退火优化后的BP神经网络,与常见的故障诊断方法相比,故障识别准确率大大提升。
