改进的神经网络算法在预测方法中研究与应用*
2023-01-06邬希可
邬希可
(华南理工大学工商管理学院 广州 510000)
1 引言
神经网络是深度学习的基础,是以人脑中的神经网络作为启发,由大量的神经元相互连接,模仿生物学神经网络结构和功能的数学模型和计算模型。神经网络包括多种算法,其中BP神经网络是目前应用最广泛的神经网络之一,主要是按照误差逆向传播算法训练的多层前馈网络,可以有效学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程,可以有效地应用于预测过程中。
分析目前专家学者对BP神经网络的研究可知,文献[1~4]将BP神经网络中的学习率调整为自适应的结构,以此加快网络的收敛速度,主要是在传统BP神经网络算法上对时变过程参数的神经元网络进行改进,但对算法的局部最小问题和预测效果方面考虑的较少。文献[5]提出最佳学习因子引入BP神经网络算法中,提升算法在执行过程中的收敛速度,达到减少网络训练步骤的目的,但是此种研究对算法执行中的极小点问题没有解决,而且改进较局限,并且在预测应用中效果不理想。文献
[6~7]利用极限学习机的方法增加结构型反馈网络,使得算法的学习速度加快,以致提升算法的预测效率,但是对预测精度考虑的较少,而且如果数据输入过多,仍然会造成算法执行过慢的现象。部分文献[8~10]针对BP神经网络算法的隐含层进行改进,改进隐含层选权重的过程,提升算法的执行效率,从而实现预测效率的提升。
综上所述,目前对神经网络算法中的BP神经网络算法研究较多,可利用BP神经网络算法实现预测的目的,但是目前对BP神经网络算法的改进有局限性,对网络参数的考虑较少,对算法预测的效率和精度的提升效果不强。
2 BP神经网络算法结构及流程
BP神经网络是由三层及以上的网络构成的,每层网络都含有许多的神经元,网络中的左侧和右侧神经元相连即可构成复杂的神经网络[11~13]。BP神经网络包括输入层、隐含层、输出层,原始的数据利用输入层输入,经过隐含层的处理,将结果传送到输出层,输出层再利用误差反传的方式对网络的参数权重进行调节,最终使得输入值和期望值相接近[14~15]。输出层再通过误差反传的方式调节不同参数的权重,进而使输入值更逼近期望值,实现不断对神经网络调节的目的,但是传统的BP神经网络算法隐含层权值的选取存在不完善的地方,会影响算法的预测效率和精确度。
BP神经网络算法主要为以下步骤:
Step1:确定模型参数;
Step2:确定模型的输入量和期望输出量;
Step3:训练网络,设定训练次数,计算各层的输入;
Step4:反向计算训练误差,修正权值和阈值,计算误差指标。
3 基于遗传算法的BP网络模型构建
3.1 模型构建思路
改进后的模型结合遗传算法和BP神经网络算法的优点,利用多层的前馈传播方式进行遗传搜索的表示方法,可以克服遗传算法和BP神经网络算法自身存在的缺陷,可以更好地利用BP神经网络的学习能力,对训练集数据集进行训练,提高检验数据集预测的准确率,同时也可以利用遗传算法的全局搜索能力强的优点,对神经网络的网络层、输入层神经节点、隐含层节点、传递函数等方面进行优化,使神经网络结构达到最优,实现预测准确率和效率的提高,模型构建思路如图1所示。
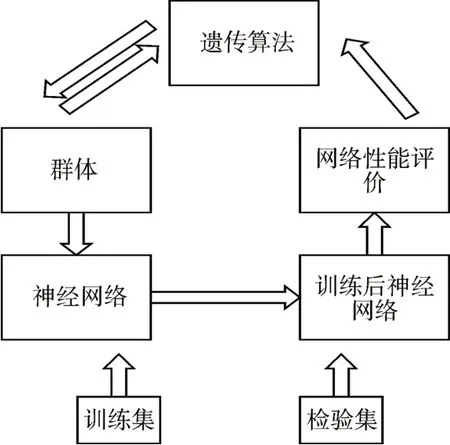
图1 模型构建思路
1)网络层数选取
神经网络中的网络层和节点数会对模型的预测结果产生重要的影响,层数选取过多会导致模型的计算压力增大,层数选取过少会导致预测结果不正确。因此,要选取合适的神经网络层数和节点数,这样不仅会提升改进后的BP神经网络算法的预测效率,也会提升改进后的BP神经网络算法的预测精度。
输入层是算法执行的起始环节,根据预测的目的,选取不同的变量对应不同的单元,即一个单元一个变量,同时为了提高算法预测的准确性,选取部分数据作为样本值,确定目标数据,根据数据比例选取输入层节点数。
隐含层节点数量的确定对算法的执行最为重要,根据映射定理,将节点与映射函数对应,无限节点可对应全部映射函数,对于有限节点来说,如果隐含层节点选取较少,会影响算法的预测准确率,使得训练时间较少,对预测规律的的学习程度不够,但是如果隐含层选取节点过多,又会影响算法的执行效率。所以,采用遗传算法优化隐含层的节点选取过程,利用二进制数值编码方式表示隐含层的神经元,最后再将神经元解码,解码为实数,用a表示神经元存在,b表示神经元不存在,也可以看作是隐含层神经元细胞数与二进制数是相同的。
2)传递函数
采用S型对数作为隐含层的传递函数,将数据进行归一化处理,输入向量与输出向量都要满足S型对数,式(1)代表隐含层的传递,式(2)代表隐含层的输出。
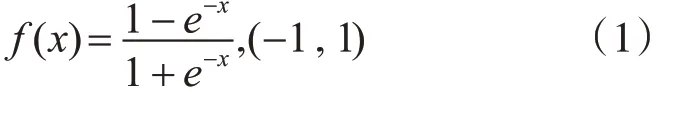
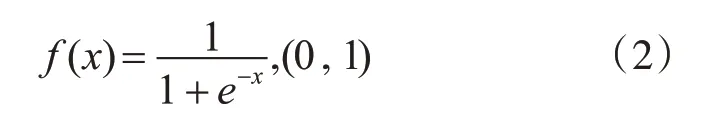
传递函数选取后,需对算法进行训练,此时利用遗传算法降低算法执行过程中的目标误差值,利用遗传算法蚁群最优个体与其它不同的个体进行交叉、变异的训练,在变异子代中找出算法中最优的个体,将此个体作为最优个体,执行下次训练,即算法寻找最优的过程,持续进行训练。
在式(3)中,P*代表最优群体,P代表当前最优个体。

在改进后的BP神经网络中,整体具有非线性映射关系,如式(4)所示。
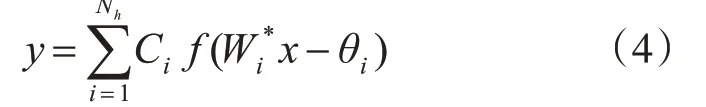
其中,(xj,tk)表示训练样本,激励函数为f,w为输入层和隐含层的连接权值,c表示隐含层输出权值,阈值为θ,ω=(W,C,θ)。
3.2 改进后算法流程
遗传算法和BP神经网络算法结合后,算法从确定初始的网络结构出发,利用遗传算法初始化种群数量,进行遗传优化,确定网络权重,并不断地调整权重。具体算法步骤如下:
Step1:确定网络结构;
Step2:初始化种群数量,进行遗传优化;
Step3:获取网络权重,计算误差;
Step4:调整网络权重;
Step5:输出结果。
4 实验结果及分析
实验数据选取某食品2015年1月-2019年12月价格数据组成数据集,共计1134组。在全部数据中,根据时间序列等方式筛选数据,将数据分成训练集和样本集,对比分析预测效果。其中,网络输入节点数为50,输出节点数1,学习速率设定0.1,算法迭代次数为6000。从算法的预测效率和预测精度两个方面分析传统的BP神经网络算法和改进后的BP神经网络算法。
1)预测效率
在实验过程中,利用相同数据量、相同数据结构的食品价格数据组,分别执行传统的算法和改进后的神经网络算法,采用计时的方式记录算法的执行时长,执行时间对比分析如表1、图2所示。

图2 执行时间对比
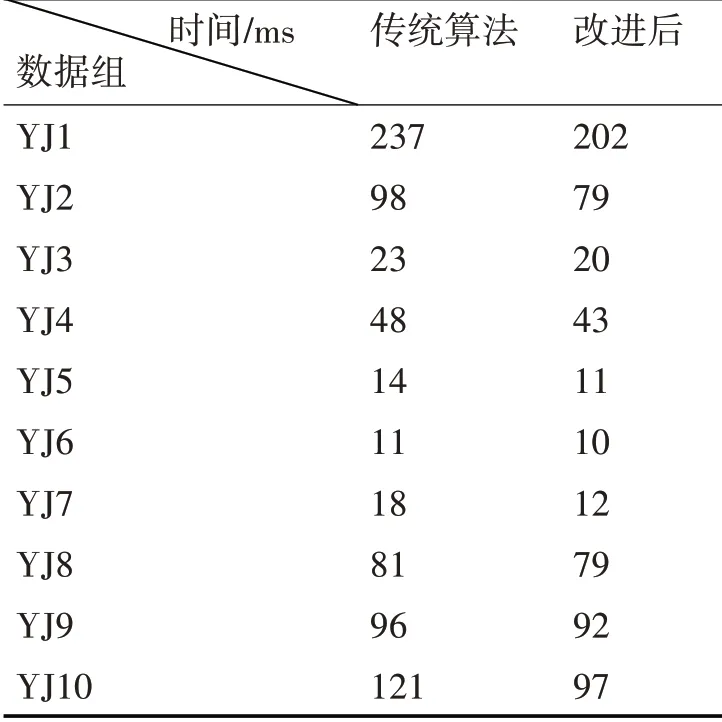
表1 执行时间对比分析
实验结果可知,结合遗传算法改进后的BP神经网络算法相比传统的BP神经网络算法在一定程度上可以节省算法的运行时间效率,可以加快算法的执行速度,提高预测的效率。
2)预测准确率
在实验过程中,对比分析算法的预测准确率要采用相同数据量、相同数据结构的食品价格数据组,实现数据对比分析的统一化,将数据组分为样本集和预测集两部分,分别执行传统算法和改进后的算法,将预测集数据与模型输出结果对比,分析算法的准确率,算法准确率对比分析如表2、图3所示。
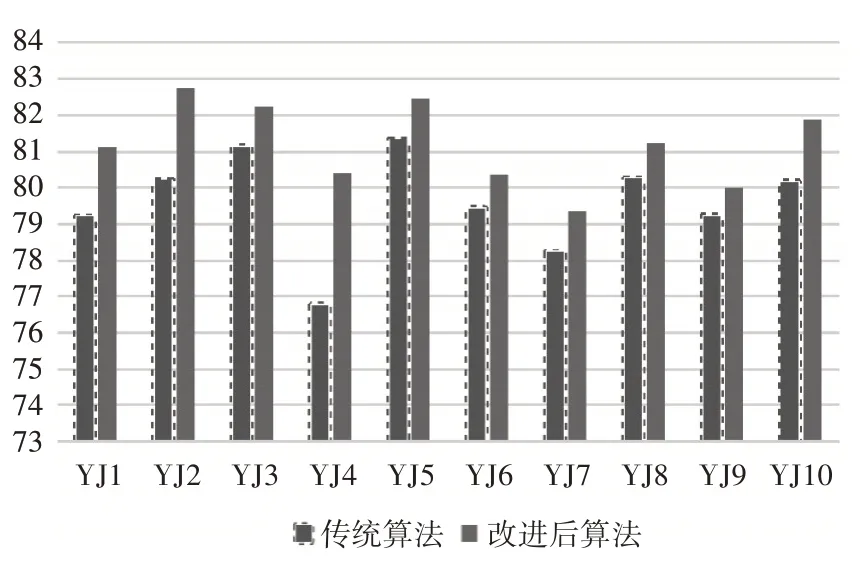
图3 算法准确率对比
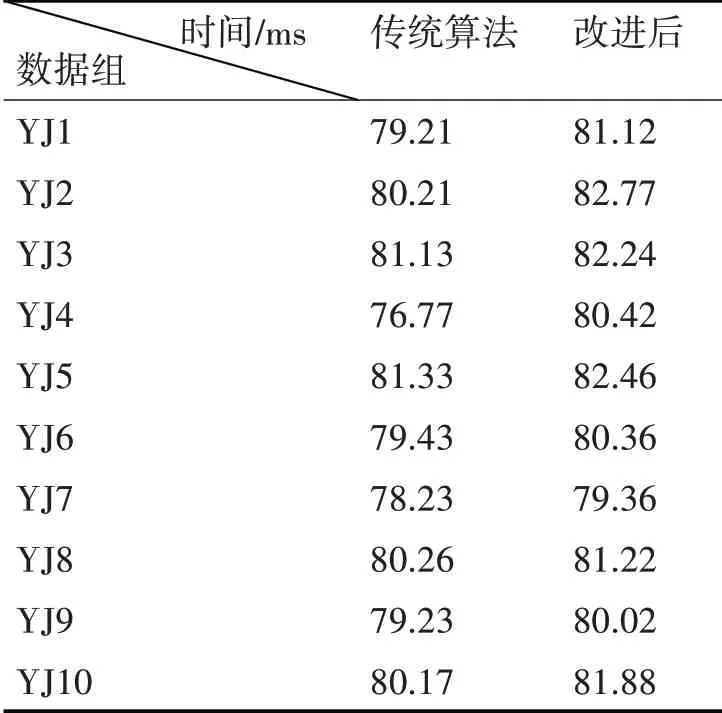
表2 算法准确率对比分析
实验结果可知,结合遗传算法改进后的BP神经网络算法相比传统的BP神经网络算法在一定程度上可以提高算法预测的准确率,使得算法在预测过程中的精确度更强,更利于神经网络算法在实际预测问题中的应用。
5 结语
本文通过对神经网络算法的分析,研究了神经网络算法中普遍用于预测的BP神经网络算法,分析传统BP神经网络算法的不足,利用遗传算法对BP神经网络进行改进,优化算法权重选取过程,提升算法的预测效率和预测精度。得到了如下结论:
1)基于遗传算法的BP神经网络算法与传统的BP神经网络算法相比,可以提高算法在预测过程中的执行时间,提高预测效率。
2)基于遗传算法的BP神经网络算法与传统的BP神经网络算法相比,可以提高算法在预测过程中的准确率,提高预测精度。
