基于PSO-GRNN的行人跌倒检测方法*

刘善良王晓原王瀚卿刘亚奇

（1.青岛科技大学机电工程学院 青岛 266000）（2.青岛科技大学智能绿色制造技术与装备协同创新中心 青岛 266000）

1 引言

随着社会和经济的发展，人口预期寿命延长，老年人数量增加，人口老龄化成为必然的趋势。老年人自身的安全防护意识不足，加之身体机能衰退，使得老年人成为跌倒行为的易发群体，跌倒是造成65岁以上老年人意外伤害和死亡的主要原因［1］。因此，跌倒的准确检测，及时的报警并救治可挽回老年人生命，避免老年人因跌倒死亡。

跌倒是指突发的、不自主的、非故意的身体位置改变，身体倒在地上或更低的平面［2］，如图1所示。在人体跌倒检测研究中，根据安装在系统中的传感器的类型，将跌倒检测方法分为基于视觉的跌倒检测方法［3～4］、基于环境的跌倒检测方法［5～6］和基于穿戴设备的跌倒检测方法［7～8］。基于穿戴设备的跌倒检测方法依靠传感器测量来区分跌倒和ADLs［9］，最常用的传感器有加速度计、陀螺仪、磁力仪和倾斜仪［10～11］。但目前已有的基于穿戴设备对跌倒行为辨识的确率不高。

本研究使用十轴姿态传感器采集行人跌倒和ADLs的腰部数据，选择加速度、角速度和高度作为特征参数，提出基于PSO-GRNN的跌倒检测方法有效提升辨识的准确率。通过Matlab对模型进行了验证，结果表明：基于PSO-GRNN的跌倒检测方法辨识精度较高，稳定性好。

2 数据采集及处理

本文使用十轴姿态传感器（JY901B）采集运动数据。将传感器佩戴于被测者腰部，采集被测者跌倒和ADLs行为的姿态数据。

2.1 实验设计

人体跌倒时，身体处于加速状态，加速度、角度、角速度和高度变化明显。本研究选择三轴加速度、三轴角速度、高度作为特征参数。腰部是人体力量的中心，且腰部的加速度计的跌倒检测精度更高［12］。因此，本研究以腰部为坐标原点，以正前方为Z轴正方向，根据右手法则，建立笛卡尔坐标系，如图2所示。传感器佩戴位置，如图3所示。

图3 实验设备佩戴图

将跌倒分为前侧、左侧、右侧、后侧跌倒；将ADLs分为类跌倒行为和正常行为，其中类跌倒行为包括跳跃、下蹲、上下楼梯等，这些行为在一定程度上影响跌倒检测；正常行为包括行走、跑、坐-躺、站-坐，这些行为与跌倒差异较大。

使用传感器采集行人跌倒和ADLs的三轴加速度（ax，ay，az）、三轴角速度（ωx，ωy，ωz）和高度（h）数据。招募40名大学生进行实验，并给与一定报酬。其中女性10人，160cm及以下5人。在地面放置4张90cm*200cm*1.5cm的瑜伽垫，参与者佩戴护膝，防止受伤。每位被测者重复20组各类型跌倒，10组各类型的ADLs。

2.2 数据处理

根据所采集的人体运动的三轴加速度、三轴角速度和高度，求解合加速度、合角速度和高度变化量，公式如下：

1）合加速度

2）合角速度

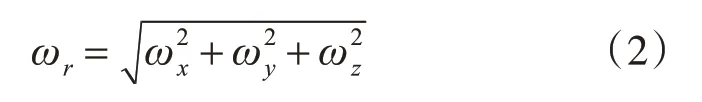
3）高度变化

在数据集中，4种跌倒和3种类跌倒行为各选择20个连续的数据点；6种正常行为各选择10个连续的数据点，组合形成人体不同动作数据特征图，如图4所示。

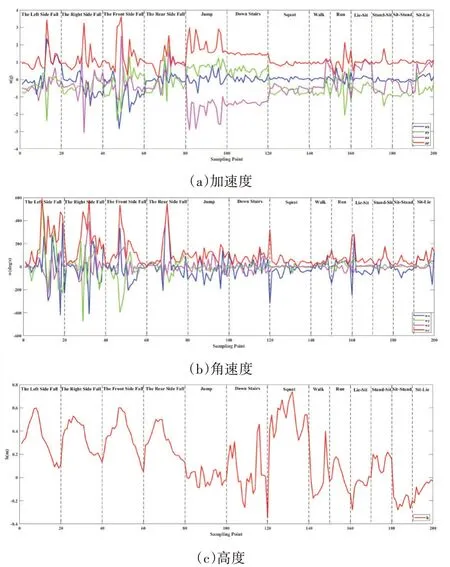
图4 人体不同动作数据特征

图4（a）为人体各运动的加速度变化图，图4（b）为人体各运动的角速度变化图，图4（c）为人体各运动的高度变化图。

在实验数据集中，选取200组特征数据点创建数据集。其中160组作为训练数据集XA，40组作为测试数据集XB，同时建立对应的标签数据YA、YB。训练集和测试集中各行为类型对应的数据个数，如表1所示。

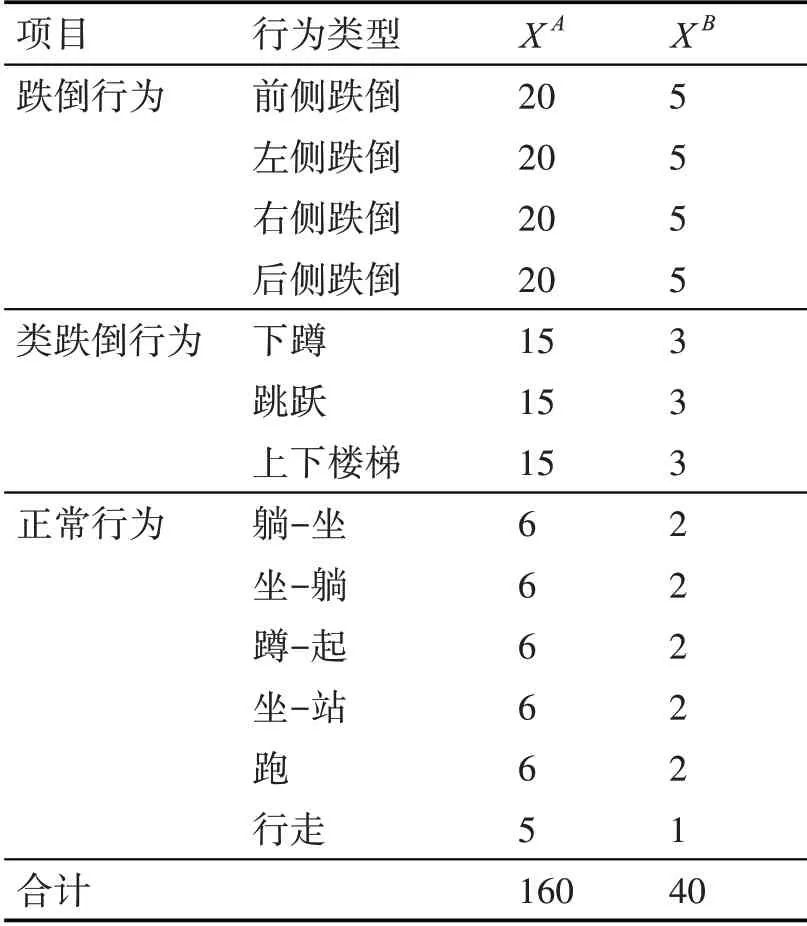
表1 各行为样本数量表

3 PSO-GRNN跌倒辨识模型的构建方法

3.1 GRNN原理

GRNN［13］由输入层、模式层、求和层和输出层构成，如图5所示。

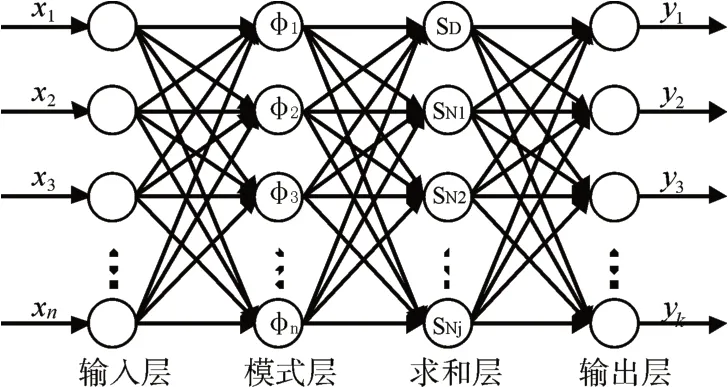
图5 GRNN网络结构图

1）输入层

选择合加速度ai、合角速度ωi和高度ℎi为特征参数，对应网络输入

2）模式层神经元传递函数

式中，σ为光滑因子。

3）求和层

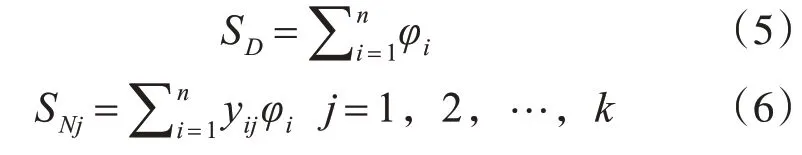
式中：yij为第i个输出Yi中的第j个元素。

4）输出层

3.2 PSO算法

PSO算法［14］通过粒子调整自己的位置来搜索最优解。粒子的最优解记为pbest，粒子群的最优解记为gbest。粒子的速度为vi，粒子的位置为zi，每个粒子根据下式更新自己的速度和位置。

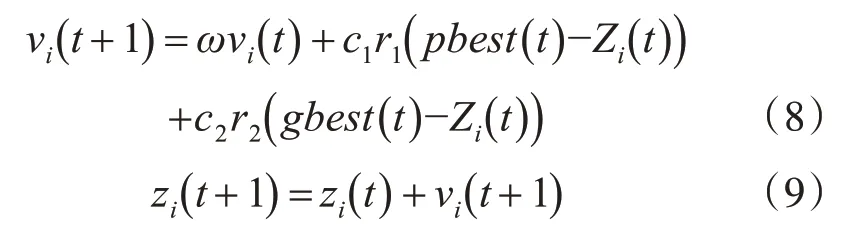
式中，vi(t+1)表示第i个粒子在t+1次迭代的速度，ω为惯性权重，c1和c2为加速度因子，r1和r2为[0,1]间的随机数。

3.3 PSO-GRNN模型

通过粒子群算法寻优，找到最优光滑因子，构建PSO-GRNN神经网络模型［15］。导入XA、XB和标签数据YA、YB，进行模型训练和测试，步骤如图6所示。

图6 PSO优化GRNN网络的基本框架图

1）初始化种群及粒子的速度和位置，设置粒子群算法的基本参数。

2）将粒子位置映射到GRNN网络中：以gbest为光滑因子spread，构建GRNN网络模型：net=newgrnn(P,T,spread)。P为神经网络的输入，T为神经网络的输出。

3）训练GRNN，并计算粒子所在位置的适应度值。适应度表示为输出值和实际值的均方根误差，计算公式如下：

式中：为中的第i组数据对应的标签，yA为网络实际输出。

4）更新pbest、gbest，若适应度优于之前的最优适应度，则更新pbest、gbest。

5）根据式（9）和式（10）对粒子的当前位置和速度进行更新和调整。

6）判断是否达到最大迭代次数，如果达到则保存最优GRNN模型，并进行模型的测试，如没有则返回2）。

4 模型验证与对比

本研究使用Matlab对构建的PSO-GRNN跌倒检测模型进行训练和验证。最后，选择支持向量机模型和BP神经网络模型进行对比实验。

4.1 PSO-GRNN模型的训练和测试

1）模型的训练

（1）设置PSO算法基本参数，如图7所示。将粒子位置映射到网络，并将XA及YA导入网络。为防止盲目搜索，将粒子位置和速度限制在

图7 模型参数设置图

（2）通过训练，在迭代至第121次时达到最优位置92.948；在迭代至第146次时达到最优适应度值0.0038。如图8所示。

图8 模型训练结果图

2）模型的测试

（1）将XB和YB导入网络，进行网络测试。重复20次测试，其中一组测试结果如图9所示，其中输出值为1表示行人跌倒；输出值为0表示行人未跌倒。图9中，第1和10组数据测试值与实际值差异较大，可确定为辨识错误；第25和36组数据的测试值与实际值存在可接受误差，故不属于辨识错误。

图9 训练结果图

经过测试，目标精度为0.005的情况下，平均正确率为0.95。

（2）为了验证粒子群参数对PSO-GRNN网络预测结果的影响，更改粒子Vmax、Vmin，c1、c2对跌倒行为进行预测，平均预测结果如表2所示。由表2可知，在PSO-GRNN跌倒检测的模型中，当粒子速度在[- 20,20]时，c1=c2=0.75时，跌倒检测的平均正确率最高，效果最好，误差最低。

表2 不同粒子群参数下的预测结果

（3）在除XA和XB外的实验数据中，提取前侧、右侧、左侧、后侧跌倒数据各50组，构建新测试数据集，导入训练好的模型中测试，结果如图10所示。

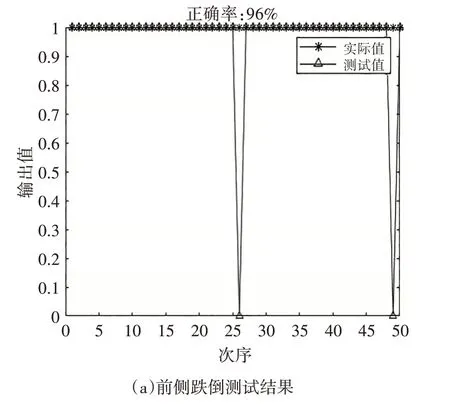
图10 各类型跌倒辨识的正确率

由图10可得，PSO-GRNN模型对各类跌倒的辨识正确率分别为前侧96%；右侧98%；后侧98%；左侧仅为92%。初步分析出现这种现象可能是，实验时率先进行的左侧跌倒，被测者在跌倒时可能有一些防备，导致跌倒的数据出现偏差。

4.2 对比实验

为验证PSO-GRNN的优越性，将XA、YA、XB、YB导入支持向量机（SVM）［16］和BP神经网络（BPNN）检测模型进行对比。

1）SVM跌倒检测模型

选择径向基函数作为核函数，经过多次训练和测试，结果如图11所示。由图可知，出现3组辨识错误，最终得到SVM对跌倒行为的检测正确率为92.5%。

图11 SVM模型跌倒测试结果

2）BPNN跌倒检测模型

选择拟牛顿法训练BPNN，最大训练次数为1000次，训练精度（goal）分别为10-1、10-2、10-3、10-4、10-5，学习率（lr）选择0.1、0.2，跌倒行为预测的正确率（RBP），如表3所示。

表3 BP神经网络预测效果

由表3可知，经过参数的调整优化，BPNN模型检测的准确率为92.25%，但学习速度慢，容易陷入局部极小值。

通过上述对比实验，相比于SVM和BPNN模型，PSO-GRNN模型寻优过程简单，精确率高，稳定性好。

5 结语

本文提出一种基于粒子群优化广义神经网络的跌倒检测方法。通过采集人体腰部的三轴加速度、三轴角速度和高度数据，分析行人跌倒的特征。构建PSO-GRNN跌倒检测模型，通过Matlab对模型进行训练和测试。结果表明：该模型能有效地识别出行人跌倒行为。在目标精度为0.005情况下，平均准确率能够达到了95%。未来工作可以对行人类型进行细致的划分，通过对不同类型的行人跌倒行为进行分析，可以更加深入研究行人跌倒的规律，进一步优化检测模型。