运动参数对光伏电池输出特性影响研究*

张亚飞 王天宇 陶俊鹏 彭乐乐 郑树彬

（上海工程技术大学城市轨道交通学院 上海 201620）

1 引言

太阳能作为一种清洁、零碳排放能源，其大规模推广与应用有助于实现碳达峰［1］和碳中和［2］目标。光伏电池是光伏发电技术的核心组件［3］，已广泛应用于海上光伏电站、无人机、交通运输等运动载体［4～5］上。然而，太阳能电池板表面接收到的光照强度会随载体运动状态改变而时刻发生变化，从而引起光伏电池输出特性的波动。因此，研究载体运动参数对光伏电池输出特性的影响具有重要意义。

国内外学界对载体运动状态下光伏电池输出特性研究较少。何啸等［6］建立海洋浮体模型分析海浪运动对光伏电池光照性能的影响，得到光伏电池在海浪影响下所接收到的太阳辐射能量，获取了海浪运动对浮体光伏发电中光伏电池的输出特性的影响，然而并未考虑海浪运动是如何影响光伏组件输出特性的；朱立宏等［7］利用光伏组件产生的功率模型并结合光伏电池转换效率模型［8］、组件表面温度模型［9］、太阳光辐射模型［10］等，研究了飞行速度、高度、时间及区域等飞行状态参数对光伏电池组件输出性能的影响，然而并未考虑飞行器姿态信息对算法本身的影响，使得在复杂运动条件下获得的动态输出特性精度较低。这些方法虽然能间接获取光伏电池在运动状态下输出特性，但均为明确给出运动参数与输出特性的之间影响关系。

针对以上问题，本文选取列车为运动载体，使用惯性测量单元采集列车运动参数；在光伏电池单二极管五参数模型基础上，利用电池板参数与光照强度及温度耦合关系建立运动状态下光伏电池输出模型；基于随机森林权重算法求出光伏电池最大功率点功率与各运动参数之间的权重。最后通过SIMPACK和Matlab/Simulink仿真软件搭建运动状态下光伏电池仿真模型。仿真结果表明，载体运动参数与最大功率之间存在耦合关系，且对光伏组件输出特性影响不可忽略。

2 运动状态下光伏电池输出特性模型

2.1 静止状态下光伏电池数学模型

光伏电池单二极管等效电路模型［11］如图1所示，包含一个光电流源、二极管D、串联电阻Rs和并联电阻Rsh。

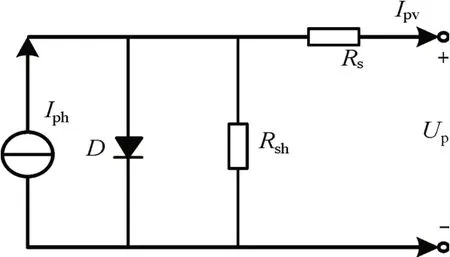
图1 光伏电池单二极管等效电路模型

根据单二极管等效电路，可得光伏组件的输出电流Ipv，其数学模型［12］可表示为

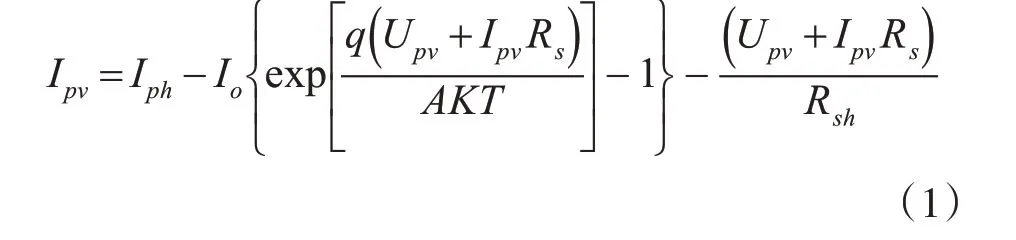
其中，Ipv为光伏电池输出电流，A；Iph为光伏电池光生电流，A；Io为二极管反向饱和电流，A；Upv为光伏电池输出电压，V；q为电子电荷，1.6×10-19C；K为玻尔兹曼常数，1.38×10-23J/K；A为二极管理想因子；T为绝对温度，K；Rs为等效串联电阻，Ω；Rsh为等效并联电阻，Ω。

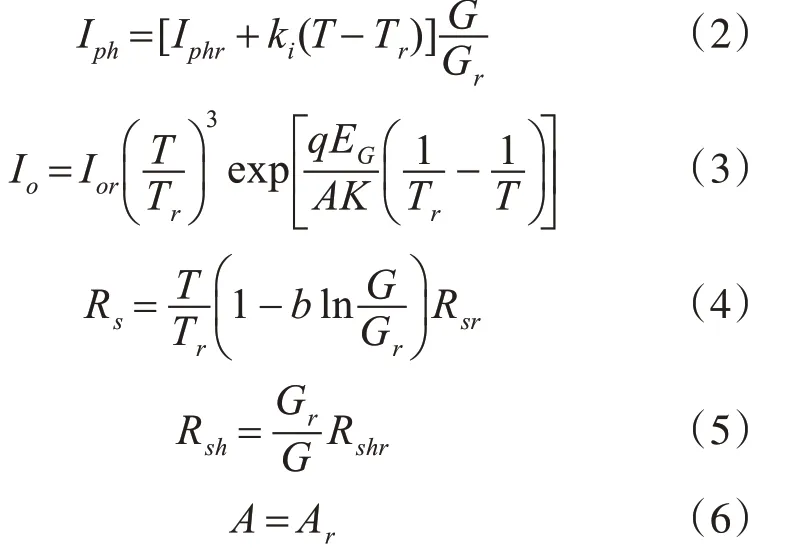
其中，Iphr为标准状况（T=25℃，G=1000 W/m2）下光伏电池光生电流，A；ki为短路电流温度系数；T为电池温度，℃；Tr为标准状况下温度值，25℃；G为光照强度，W/m2；Gr为标准情况下的光照强度，1000W/m2；Ior为标准状况下二极管反向饱和电流，A；EG为标准状况下光伏电池材料能带宽度，1.12eV。

2.2 运动状态下光伏电池输出模型

光伏电池安装在运动载体顶部，电池板表面接收到的光照强度会随载体运动时刻发生改变，从而影响光伏组件的输出特性，如图2所示。

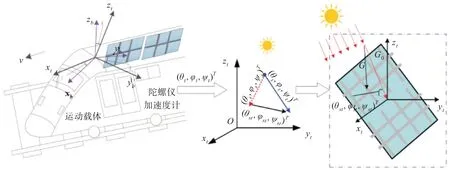
图2 载体运动状态下光照强度与角度变化图

其中，[θbφbψb]T为测量所得光伏电池与载体坐标系三轴夹角；[θtφtψt]T为光伏电池与地理坐标系三轴夹角；其中为姿态矩阵，用欧拉角表示如式（8）：

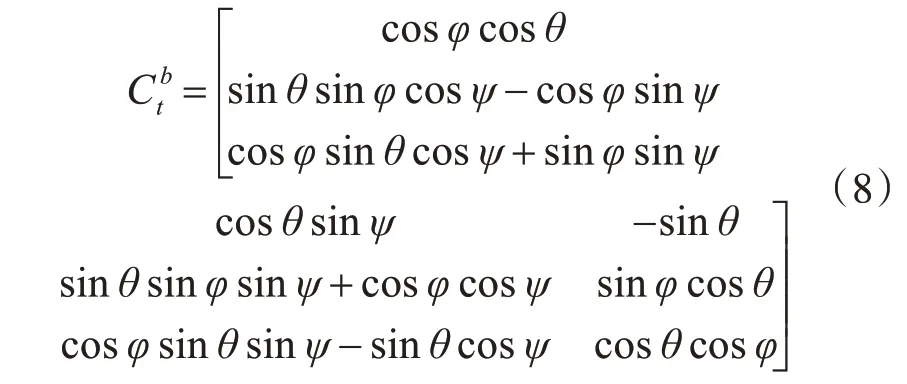
使任意辐射强度G0照射在电池板上，如图2所示，设光照强度与地面坐标系三轴初始夹角故光照强度与太阳能电池板的夹角如式（9），太阳能电池板表面接收的光照强度G大小如式（10）：

将式（10）带入到式（2）～式（6）可得到光伏电池板参数，再将此关系式代入式（1）可得载体当前运动状态下光伏电池输出特性模型。

3 基于随机森林运动参数影响分析

3.1 随机森林

随机森林算法［15］（RF）是一种基于统计学习理论的智能分类算法，其原理是利用Bootstrap抽样方法将K个样本集从原始样本集中有放回地抽取出来，并对K个样本集分别建立多个决策树组成一片随机森林，最后计算相应分类结果求平均，图3为随机森林算法基本结构。

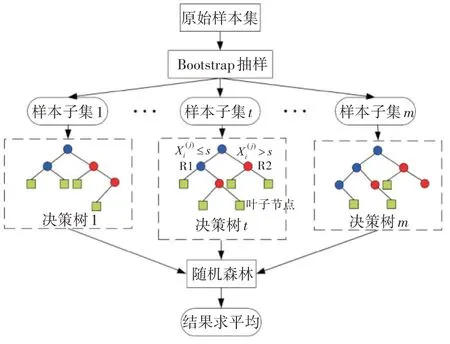
图3 随机森林算法基本结构

3.2 随机森林权重计算

随机森林算法的一个重要特征是通过计算输入变量的权重［16］来分析变量之间的重要性，为了解各运动参数与Pm的实际贡献情况，使用随机森林权重算法计算Pm与各运动参数之间的权重，设原始样本数据集为T=（y,x1,x2,…,xi），其中，xi表示自变量构成的多维输入量；y为因变量输入量，计算过程为

1）通过随机森林Bootstrap采样得到m个样本数据子集，对应得到m个OOBm数据集；

2）使用第t（t=1,2,…,m）个样本子集，训练决策树Ct，并计算第t个OOBm数据集的准确率

Lt；

3）无规则地改变第t个OOBm数据所有样本j（j=1,2,…,i）的数据顺序，并利用步骤2）中Ct重新计算第t个样本子集的OOBm准确率Lt,j；

4）则变量j(j=1,2,…,i)的权重计算公式如式（11）：

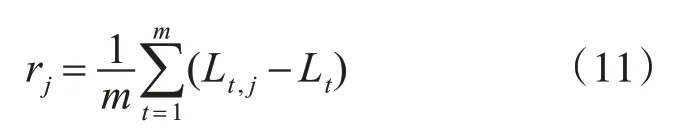
准确率计算公式如式（12），式中noob(k)为第k个OOBm袋外数据集的样本数量和为第k个OOBm袋外数据集中的第t个样本数据的真实值、扰动前预测值和扰动后预测值。

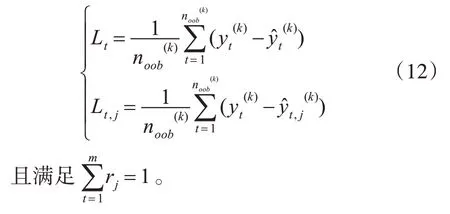
4 实验验证及结果分析

为了获取运行参数对光伏电池输出功率的影响大小，首先使用多体动力学软件SIMPACK构建车辆/轨道动力学模型［17］，在模型中加入德国轨道谱作为模型振动激励，进行仿真获取车辆运动状态下的角速度和加速度测量值。

根据式（1）～（6）将光伏电池数学模型转换为仿真模型，在Matlab/Simulink平台上搭建光伏电池仿真模型，将由式（7）计算所得地理坐标系下载体姿态角作为输入变量。选取型号为Solare msx-60型光伏组件作为仿真对象，在测试温度Tr为25℃，光照强度Gr为1000W/m2时，光伏组件的开路电压Voc为21.1V，短路电流Isc为3.8A，最大功率点电压Um为17.1V，最大功率点功率Pm为60W，模型初始参数如表1所示。

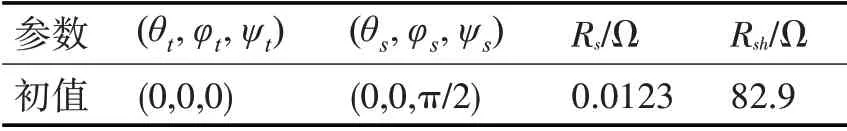
表1 运动状态下光伏电池仿真模型初始参数

表2 运动参数随机森林权重

表2结果显示Pm关于gx、gy、gz、wx、wy和wz的权重百分比分别为11.6%、3.7%、71.2%、8.2%、2.5%和2.8%。由该图又可以看出，gz的权重占比最大，达到71.2%。其余5个运动状态参数所占权重由高到低依次是gx、wx、gy、wz和wy。

采用控制变量的方法，依次剔除gx、gy、gz、wx、wy和wz并分别进行光伏电池仿真，对应所得Pm曲线如图4和图5。

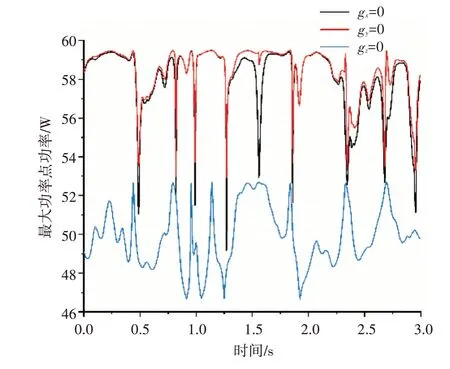
图4 剔除加速度所得最大功率点功率曲线

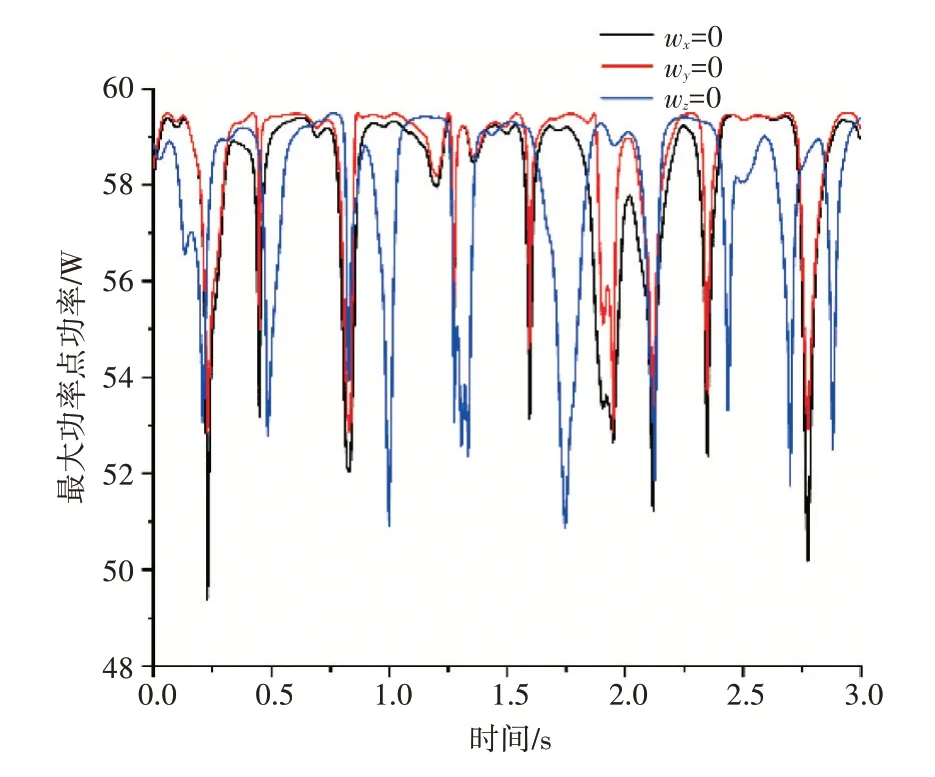
图5 剔除角速度所得最大功率点功率曲线

图4和图5为分别剔除gx、gy、gz、wx、wy和wz后的Pm曲线图，从图中可以看出当剔除gx、gy、wx、wy和wz时，Pm波动范围在0.009%～2.06%之间。当剔除gz时，Pm波动最大，最大波动率为21.288%，与权重分析结果一致，证明了权重分析方法的正确性。

5 结语

本文针对载体运动参数对光伏电池输出特性的影响进行研究，通过构建列车/轨道动力学模型以及运动状态下光伏电池仿真模型进行仿真获取载体运动参数以及光伏电池输出最大功率点功率，基于随机森林权重算法对各参数进行随机森林权重计算，采用控制变量的方法依次剔除运动参数并重新仿真分别获取对应最大功率点功率。结果表明剔除载体垂向加速度对光伏电池最大功率点功率影响最大，最大波动率为21.288%，在各运动参数中占主导。