锁相环对虚拟同步机惯量阻尼特性的影响机理研究

2023-01-06谢志文唐酿邱俊卿袁敞

电力电容器与无功补偿 2022年6期

谢志文，唐酿，2，邱俊卿，袁敞

（1.广东电网有限责任公司电力科学研究院，广州 510080：2.广东电科院能源技术有限责任公司，广州 510080；3.华北电力大学，北京 102206）

0 引言

由于环境污染和化石能源危机的日趋严重，新能源领域得到广泛的关注和发展。新能源通过逆变器并网时并未像传统旋转发电机设备一样为电网提供惯量和阻尼，随着新能源逆变并网的比例增大，会使电网频率稳定性变差。作为一种可能的解决方案，虚拟同步发电机（virtual synchronous generator，VSG）[1-5]能够在外特性上尽量模拟同步发电机的特性，可提高系统的频率稳定性[6]。1997 年，文献[7]定义了众多关于FACTS 的名词术语，其中包括“（SSG）static synchronous generator”，即使用非旋转设备模拟同步发电机。2007 年“virtual synchronous machine”的概念提出后[8]，国内外学者对虚拟同步机的相关话题展开了广泛讨论[9-14]，截至目前仍是研究热点。

在上述文献中，锁相环广泛地应用于虚拟同步机的控制系统，为逆变器提供电网相位信息，实现与电网的同步。然而有部分学者致力于锁相环的改进[15-22]，希望在保持锁相环性能的基础上，尽量削弱锁相环可能给逆变器特性带来的负面影响，但是锁相环所具有的动态特性仍会作用于虚拟同步机，改变其性能。例如文献[23]中，钟庆昌团队考虑锁相环“慢”的特性会影响虚拟同步机与电网同步的准确性，因而放弃了锁相环的使用。文献[24]也提出了类似的、不使用同步单元（锁相环）的单相虚拟同步发电机模型及控制策略。

但是另一方面，锁相环所具有的二阶特性类似于同步发电机的二阶模型，若应用合理，则可以与虚拟同步机协调控制，相辅相成。Younis 等人于2012 年提出在逆变器控制中考虑锁相环的影响，统一建立数学模型[25]，一定程度上消除了由于忽略锁相环动态带来的逆变器特性偏差。华中科技大学袁小明、胡家兵团队在2014～2016 年连续发表3 篇论文更加全面地论述了如何在模拟风机惯性控制中利用锁相环的二阶动态，并且比较了传统风机惯性控制与锁相环模拟惯性控制的优劣，采用锁相环模拟惯性实现了风机的惯性并网[26-28]。因此，锁相环能够为逆变并网系统提供惯量补充，与虚拟同步机有相似的作用，那么如果把锁相环和虚拟同步机的控制结合起来可能会有更好的控制效果。所以对于虚拟同步机来说，锁相环是一个值得深入探讨的话题。

本文考虑锁相环的动态，研究了锁相环对于虚拟同步机惯量、阻尼特性的影响机理。第1 节分析了具有代表性的三相Park 变换锁相环，然后对使用同步发电机二阶模型的虚拟同步机进行了重新建模。第2 节研究了锁相环对虚拟同步机惯量、阻尼特性影响的机理，将新模型与原模型对比，发现考虑锁相环动态的新模型能够更精确地描述当电网频率发生变化时，虚拟同步机功率的动、静态响应。并且，基于新模型的计算和仿真表明，锁相环等效增大了虚拟同步机的惯量，削弱了阻尼。论文进一步探讨了锁相环对于等效惯性时间常数和阻尼系数的定量影响。第3 节给出了相应的仿真结果，验证了考虑锁相环的虚拟同步机系统模型建立的准确性。

1 考虑锁相环的VSG系统模型

根据不同的研究角度可选择多类同步发电机模型[29]中的一种用于虚拟同步机控制。因为本文研究重点是虚拟同步发电机的惯量、阻尼特性，二阶模型可以满足要求，所以选择满足要求的二阶模型。基于所选的模型进行研究，有以下几点前提：

1）假设转子极对数为1。

2）不考虑同步发电机一次调频的影响。

3）系统频率发生改变时，没有其他扰动发生。

根据所选模型得到的虚拟同步机控制框图，见图1。图中：Udc是直流侧电容电压，文中不考虑其对系统的影响，认为其保持稳定；直流电压经三相逆变器变换后得到三相输出电压，用单相图表示；E∠δ为输出电压向量，E为A 相线电压有效值，δ为A 相线电压相位，三相电压互差120 度；L、R分别为滤波电感值和电阻值；Pe、Qe分别是虚拟同步机输出有功、无功功率；Ig是虚拟同步机并网电流；以电网电压U∠0°作为参考，U为A 相线电压有效值，0°为A 相线电压相位，三相电压互差120°；用锁相环得到电网电压相位、角频率，角频率ωg（或ωPLL）（不考虑锁相环动态时，ωg=ωPLL）用于有功-频率控制；Pref、Qref分别是有功、无功功率参考值，由控制器给定；E0是额定线电压有效值；ωref是额定频率50 Hz 对应的参考角频率；H是虚拟惯性时间常数（以下称惯性时间常数）；D是虚拟阻尼系数（以下称阻尼系数）；ω是虚拟同步机输出电压的角频率；s 是拉普拉斯算子；有功-频率控制、无功-电压控制分别输出参考电压的相角φ、相电压幅值E，经过正弦波发生器产生三相调制波电压，使用SPWM 调制与三角载波比较后得到逆变器的开关信号。其中，上标“*”均表示对应物理量的标幺值。

图1 虚拟同步机及其控制框图Fig.1 VSG and its control block diagram

1.1 忽略锁相环动态的VSG模型

虚拟同步发电机的二阶模型公式为[30]

参考文献[30]已给出不考虑锁相环动态，电网频率阶跃时，虚拟同步机输出有功功率与电网频率之间的传递函数为

式中，SE是同步功率[31]，其表达式为

式中：α=tg-1(ωL/R)为滤波电感阻抗角；为滤波电感阻抗；Sn=250 kVA 为虚拟同步机额定容量。由此，当电网频率阶跃变化时，虚拟同步机输出有功功率公式为[30]

式中，Δ 表示各物理量在稳态值附近的小扰动量。

1.2 考虑锁相环动态的VSG模型

上一节的虚拟同步机模型建立没有考虑锁相环动态对虚拟同步机的影响。但是实际工程中的锁相环多具有二阶动态响应特性，这会在电网频率发生变化时，体现在PLL 所提供的电网频率中，使默认ωg准确时得到的推导公式与实际工况产生偏差，减弱对于工程实践的指导意义。因此，本节会通过考虑锁相环动态对虚拟同步机模型进行修正，作为论文下一步分析的基础和依据。

考虑锁相环时，虚拟同步机的模型公式为

需要特别注意的是，式（1）所描述模型中的两个方程（转子运动方程和功角方程）中均含有电网频率ωg，当考虑锁相环的动态时，如式（5）所示，需要将转子运动方程中的电网角频率替换为锁相环得到的角频率ωPLL（ωPLL=GPLLωg,GPLL为锁相环传递函数），功角方程中的电网角频率则不需要改变。原因如下：

1）由图1 中的控制结构可知，转子运动方程中所使用的电网电压角频率由锁相环直接提供，所以此处应改成ωPLL。

2）功角方程中的ωg并不是由锁相环直接提供，而应该是真实的电网电压角频率，因为决定虚拟同步机输出功率的功角δ应该是虚拟同步机输出电压和真实电网电压相角的差值，其中已经包含了锁相环带来的动态特性的影响。

对式（5）求取小信号模型可得

本文的研究基于三相park 变换锁相环，其结构见图2。kpPLL、kiPLL分别是虚拟同步机锁相环PI调节器的比例、积分系数；锁相环输出频率与电网频率之间的传递函数为

图2 三相锁相环结构框图Fig.2 Structural block diagram of three-phase PLL

参考文献[32]对虚拟同步机输出功率的推导：

对式（8）中有功功率表达式求小信号模型可得

将式（7）代入式（6）后，联立式（6）、式（9）可得考虑锁相环动态的虚拟同步机输出功率和电网电压角频率之间的传递函数，如式（10）所示。

对比式（2）的传递函数，由于锁相环动态的引入，使得原本的二阶动态响应变成了四阶，从虚拟同步机惯量、阻尼特性上看，会与预设参数下期望的动态特性产生差异，对于所产生的影响将在之后的章节进行详细分析。

2 锁相环对VSG 惯量阻尼特性的影响机理研究

上文得到的传递函数式（2）、式（10）分别代表了虚拟同步机在不考虑/考虑锁相环动态两种情况下的响应特性，下文将在频域对比两种情况来研究锁相环对于虚拟同步机的特性会产生怎样的影响。

2.1 考虑锁相环动态的VSG模型

首先，对于锁相环动态的引入，可以在时域和频域两个角度进行定性分析。时域分析将在第3 章的仿真分析中给出。本节对不考虑/考虑锁相环的两种情况下，对具有相同阻尼、惯性参数的虚拟同步机的频率响应特性作对比，见图3。并且通过2.1.1、2.1.2 的讨论对锁相环给虚拟同步机系统带来的影响形成直观的定性结论，作为下节定量分析的基础。阻尼系数、惯性时间常数对虚拟同步机频率特性的影响见图4。

图3 考虑/不考虑PLL动态虚拟同步机频率特性Fig.3 Frequency characteristics of VSG with/without considering PLL

2.1.1 阻尼系数对虚拟同步机频率特性的影响

如图4（a）所示，根据传递函数式（2），绘制当虚拟同步机的虚拟惯性时间常数H=0.5 s，阻尼系数分别为D=10、20、30 时的三组频率特性曲线。当D增大时，幅频特性低频段和高频段基本不受影响，中频段转折频率不变，但转折频率对应的幅值随D增大而减小；相频特性曲线在转折频率处穿越180°，穿越的斜率随D增大而减小。对比图3，考虑锁相环动态时，转折频率对应的幅值变大，对应的相位穿越180°斜率变大，所以可以定性认为，锁相环动态的引入，等效减小了虚拟同步机的阻尼系数。

2.1.2 虚拟惯性时间常数对虚拟同步机频率特性的影响

如图4（b）所示，根据传递函数式（2），绘制当虚拟同步机虚拟惯性时间常数H=0.5、0.9、1.3 s，阻尼系数D=20 时的三组频率特性曲线。当H增大时，幅频特性和相频特性的高频段变化不明显，相频特性的低频段变化不大。但是幅频特性的低频段为三条平行线，受H影响较大。转折频率随着H的增大逐渐变小。对比图3，在锁相环的作用下，在幅频特性的低频段是一条幅值较高的平行线，并且转折频率相对变小，因此可以定性认为，锁相环的动态使得虚拟同步机的虚拟惯性时间常数等效增大。

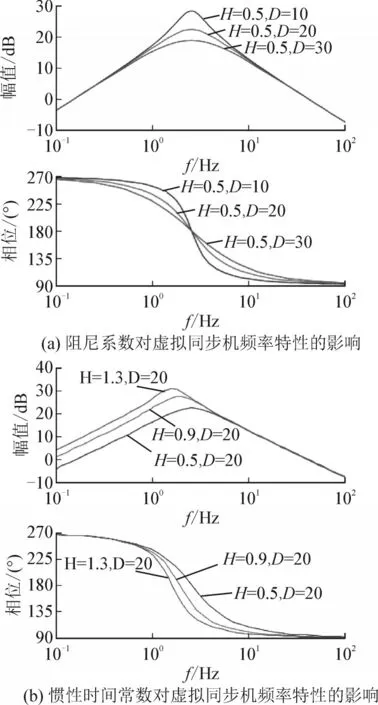
图4 阻尼系数、惯性时间常数对虚拟同步机频率特性的影响Fig.4 Influence of damping coefficient and inertia time constant frequency characteristic of on VSG

2.2 含锁相环VSG系统的等效惯量阻尼参数

上一节已经通过两组分析结果定性地给出了虚拟同步机在考虑锁相环动态的情况下，惯量、阻尼特性会受到怎样的影响。初步的结论是，保持预设虚拟惯性时间常数H和阻尼系数D不变的情况下，锁相环的加入会等效增大虚拟同步机的H、减小虚拟同步机的D，造成惯量增大，阻尼减小的现象。本节将通过理论分析检验并解释这一定性结论，得到锁相环加入后对H和D影响的量化分析结果。

本节根据式（2）和式（10）的传递函数分别计算了不考虑/考虑锁相环动态时的幅频特性和相频特性，通过数学分析，求解加入锁相环后系统的等效惯量和阻尼。首先，分别计算两种情况下的系统频率特性。假设传递函数写成复数形式为：A+jB，则有：

2.2.1 不考虑锁相环时系统频率特性计算

传递函数写成复数形式为

则频率特性公式为

对照图4（a）、4（b）可知，由于相频特性穿过180°时的转折频率对应的是幅频特性的最高点，此时，对应的情况是式（13）分子为零。由于分子与阻尼系数D无关，与H有关，所以当D变化时，转折频率始终不变，H越大，转折频率越小。幅频特性曲线在D变化时，仅有转折频率对应的峰值变化，而低频和高频都几乎重合，原因是幅频特性表达式根号下的分母在高频段、低频段分别由角频率的4 次方项和常数项主导；分子仅有一项，而且这3 项均不含有参数D，所以与D几乎无关。而在中频段，分母中的角频率2 次方项不可忽略，D越大，则幅值越小。在低频段，分母由常数项主导，不含H，分子的H2项决定了低频段幅频特性随H变化呈现出一组平行线。在高频段，分母由H项主导，其影响与分子抵消，所以高频段的幅频特性不受H参数的影响。

2.2.2 考虑锁相环动态时系统频率特性计算

传递函数写成复数形式的公式为

图5（a）、5（b）分别是考虑锁相环动态时，虚拟同步机阻尼、虚拟惯量参数对其频率特性的影响曲线，可以看到，与不考虑锁相环时各个频率段受H、D的影响类似。原因仍与各频段主导项是否含H、D有关。例如，低频段分子的主导项是角频率的平方项，含有H；分母是常数项，不含H，因此会随H变化呈现平行直线，但是都不含D，所以D变化时低频段基本不受影响；又如，在高频段，分子分母的主导项分别是角频率的6 次方和8 次方项，均不含D，并且H次数相同，效果抵消，所以H变化时高频段基本不受影响。

图5 锁相环动态时阻尼系数、惯性时间常数对频率特性的影响Fig.5 Influence of dynamic damping coefficient and inertia time constant of PLL on frequency characteristic

至此，仍是定性的结论，结合频率特性的表达式进行简单的数据分析，解释了H、D参数与频率特性之间的关系。根据自动控制原理的基本常识，系统的相频特性主要决定了系统的相位裕量，而由图3 可知，是否考虑锁相环动态，系统的相频特性在高频段基本重合，并且幅频特性过零点对应的相位也变化不大，因此锁相环对于相频特性（相位裕量）影响较小，对于幅频特性所决定的带宽、稳态误差等性能影响较大。因此，主要通过对幅频特性的分析来求解考虑锁相环时系统的等效惯量和阻尼。

首先，将2.2.1、2.2.2 两节的幅频特性表达式进行适当化简。系统的性能主要由低频段特性决定，因此，对式（15）进行低频段等效，得到其低频等效幅频特性如式（17）所示。

式（17）的等效并没有忽略分子中的角频率6 次方和4 次方项，因为这两项在低频段末段、低频段与中频段相接处已有较为明显的影响，为了更加准确地等效，在此不做忽略。

求解等效惯性时间常数和阻尼系数的方法是，令式（17）与式（12）相等，式（12）中代入考虑锁相环后的等效惯性时间常数Hx和等效阻尼系数Dx，式（17）中代入原本的虚拟同步机预设参数H0、D0，对应相等后，代入低频段（0～1 Hz）之间靠近中低频段边界频率的0.7 Hz 对应的角频率，求解Hx、Dx解集，将解集代入不考虑锁相环动态的式（2）绘制频率特性图，取其中一组能够与根据式（10）所绘制的、考虑锁相环动态时的频率特性图对应情况最好的一组作为最终的等效参数。例如，含锁相环的虚拟同步机运行参数为：H0=0.5；D0=20；kpPLL=10，kiPLL=100；R=0.5；L=2 mH；ωref=100 π，将其分别代入式（17）与式（12）求解方程，经过比较得到最好的一组等效参数为：Hx=0.77 s；Dx=9.88。

将Hx，Dx代入不考虑锁相环动态时的虚拟同步机模型中、H0，D0代入考虑锁相环动态的虚拟同步机模型中，绘制对比频率特性曲线见图6。

图6 频率特性对比图Fig.6 Comparison diagram of frequency characteristic

从图6 可以看到在全频率范围内，幅频特性的等效性较好，低频段的相似保证了稳态误差的一致性；高、低频段幅频特性过零点也较为接近，保证了带宽的一致，两种情况下动态响应速度较为接近；中频段的幅频特性高点以及对应的转折频率也基本相同。因此，可以认为此时求解得到的等效虚拟同步机运行参数，H0=0.77，D0=0.98 应用于不考虑锁相环的虚拟同步机模型，能够最为接近地等效于H0=0.5，D0=20 时考虑锁相环动态的VSG 模型。也就是说，加入锁相环之后，虚拟同步机的虚拟惯性时间常数相对于按照不考虑锁相环时所配置的期望数值增大了54%，阻尼系数减小了50.6%。

如此大范围的运行参数值变动会对虚拟同步机的运行特性造成很大的影响。当然，算例中所用的锁相环参数使得其二阶动态较为明显，因此影响较大。但是，实际工况中的锁相环根据性能要求会有不同的参数配置组合，因此锁相环对于虚拟同步机的特性影响是不可忽略的。

从另一角度看，锁相环所带来的等效特性可以加以利用，在不要求锁相速度的前提下，可以利用锁相环的“慢速”动态特性，改变虚拟同步机惯量、阻尼相关的选择范围。在原来的两个可调参数（D、H）的基础上，增加了一组锁相环的PI 参数（kpPLL、kiPLL）。

3 仿真验证

在PSCAD/EMTDC 中搭建的仿真系统参数见表1，拓扑见图7。本章主要验证考虑锁相环的VSG 系统建模的准确性以及锁相环对VSG 系统影响定性分析、定量分析的准确性。

表1 仿真系统参数Table 1 Parameters of simulation system

图7 仿真系统图Fig.7 Simulation system diagram

3.1 考虑锁相环动态的VSG模型验证

当虚拟同步机系统参数为H=0.5 s，D=20，kpPLL=10，kiPLL=100 时，将不考虑/考虑PLL 的时域阶跃响应理论分析曲线绘制在同一图中，见图8（a），两种情况下的理论分析存在较大差距。对应图3 所示的系统频率响应，时域仿真得到与频域分析一致的结果：由于会受到锁相环的影响，因此若在理论分析中忽略锁相环动态，实际表现的特性与预设惯量、阻尼参数下的期望特性不相符，存在较大差距。

经过第1 章对虚拟同步机系统进行重新建模之后，理论分析考虑了锁相环的动态，得到的时域阶跃响应与时域仿真的结果能够完全对应，见图8（b）。因此，本文所得到的考虑锁相环动态的模型能够准确描述含有锁相环的虚拟同步机系统的动态特性。

图8 PLL动态理论分析与时域仿真对照Fig.8 Comparison between dynamic theory analysis and time domain simulation of PLL

3.2 锁相环对VSG惯量阻尼特性的影响

第2 章2.1 节从频域的角度定性分析了锁相环对系统惯量阻尼特性的影响，本节将从时域仿真的角度分析，印证频域分析得到的结论。

不考虑/考虑PLL 时虚拟同步机时域阶跃仿真见图9。图9 给出了与图8（a）相对应的时域仿真结果，可以看到锁相环的动态会影响系统整体的动态性能，偏离预设参数下的期望特性。本节将使用与2.1 节类似的思路，将VSG 系统惯量、阻尼参数分别变化时，时域阶跃响应的变化趋势，与考虑锁相环动态后相对于不包含锁相环动态的系统时域阶跃响应的变化趋势进行了对比，得到了与2.1 节相同的结论。

图9 不考虑/考虑PLL时虚拟同步机时域阶跃仿真Fig.9 Time-domain step simulation of VSG without/with considering PLL

3.2.1 阻尼系数对虚拟同步机时域阶跃响应特性的影响

阻尼、惯性时间常数对虚拟同步机阶跃响应影响见图10。如图10（a）所示，电网频率阶跃时，H=0.5 s，D=10、20、30 虚拟同步机输出有功功率的3 条响应曲线。可以看到，随着D的增大，输出功率的峰值减小，并且达到稳态的时间变短，功率峰值对应的时刻有左移的趋势。对比图9，在锁相环影响下，虚拟同步机的输出功率峰值增加，稳定时间也同时变长，并且峰值也略有右移的趋势，定性来看，锁相环等效减小了阻尼系数。

图10 阻尼、惯性时间常数对虚拟同步机阶跃响应影响Fig.10 Influence of damping and inertia time constant on step response of VSG

3.2.2 惯性时间常数对虚拟同步机阶跃响应特性的影响

如图10（b）所示，电网频率阶跃时，H=0.5、0.9、1.3 s，D=20 虚拟同步机输出有功功率的3 条响应曲线。可以看到，随着H的增大，输出功率的峰值增大，并且达到稳态的时间变常，功率峰值对应的时刻有右移的趋势。对比图9，在锁相环影响下，虚拟同步机的输出功率峰值增加，稳定时间也同时变长，并且峰值也略有右移的趋势，定性来看，锁相环等效增大了虚拟惯性时间常数。