基于抗差状态估计的配电网运行状态诊断与分析
2023-01-06黄天敏
黄天敏
(广东电网有限责任公司韶关供电局,广东 韶关 512000)
0 引言
随着透明电网、泛在电力物联网等理念的发展,利用配用电大数据进行配电网的运行状态诊断成为智能配电网的主要趋势[1-2]。配电网运行状态诊断能够及时发现薄弱环节、给出诊断方案以降低运行风险,而当前存在配网数据冗余度不高、质量参差不齐等局限性问题。现有配网系统中量测数据源逐渐呈多元化,同步相量测量单元(phasor measurement unit,PMU)、高级量测体系(advanced measurement infrastructure,AMI)与传统的配网数据采集与监视控制系统(supervisory control and data acquisition,SCADA)共同构成配电网混合量测系统,为配电网的高级应用提供数据基础[3-4]。在配网量测数据冗余度提高的基础上,依托配电网状态估计[5-6](distribution state estimator,DSE)对配电网的运行状态进行诊断分析,能够为电网运行人员提供故障预警数据支持和风险预判技术支持。
近年来有关配电网诊断方法的文献多是聚焦于大数据、数据挖掘以及数据融合等新技术,文献[7]提出基于大数据的配电网诊断方法,构建基于大数据技术的配电网诊断平台软件,实现配电网诊断是以海量配网数据做决策支撑的。文献[8]对配电网历史数据及模型信息深入挖掘,建立设备状态诊断模型和评价体系,实现对设备故障评估和预警分析。文献[9]对多源异构数据进行分类组合与融合,建立诊断规则判断配电网的运行状态。文献[10]提出了基于多源数据信息融合的电力系统主网和配网故障智能诊断技术,大幅提高故障分析和处理的效率。对于配网诊断前一环节的运行状态评估方面,研究学者主要集中在权重计算方法上,文献[11]采用AHPDelphi 法确定各指标的权重因子,但该方法的主观性过强。文献[12]提出将改进AHP 和CRITIC 法所求的主、客观权重相结合。但数据质量问题往往直接影响到诊断和评估的结果,上述文献对此探讨不多。
为解决因数据缺失或错误信息导致配电网运行状态评估不准确的问题,近年来加权最小绝对值(weighted least absolute value,WLAV)抗差估计器引起了较多的关注,该方法能够保证多个量测量的残差为零,具有较好的抗差性[13-16]。将WLAV 抗差状态估计作为配电网运行状态诊断分析的数据基础,可保证计算出的配网运行状态指标的准确性。由于单一的数据源难以实现全网的可观测性,需要对多源量测数据进行融合处理以提高量测冗余度。目前不少学者在数据融合技术方面的应用研究已经取得一些成果[17],文献[3]针对智能配电网混合量测体系架构中的数据提出了一种统一信息模型,实现多源数据信息的融合。但不同数据的时标信息具有不同程度的差异,生数据难以直接用于DSE中。文献[18]提出了一种具有相量测量单元(PMU)信息的配电网络分布式状态估计,但未考虑AMI 量测仅对SCADA 和PMU 量测的数据进行融合。
为此,本文提出将抗差状态估计方法应用到配电网运行状态诊断分析中。通过将配电网混合量测系统的PMU、AMI 和SCADA 量测数据进行融合处理,建立改进WLAV 抗差状态估计模型进行配网状态估计,将估计结果用于“站-线-变-户”运行状态的指标计算,进而对配电网各层级的运行状态进行评估并给出诊断方案,最后通过仿真分析对本文所提方法的有效性进行了验证。
1 基于多源数据融合的配网状态估计
本文在对配电网进行状态估计前需对配网中的多源量测数据进行融合处理,提高量测冗余度以保证DSE 有充足的数据源。
1.1 多源数据融合方法
1.1.1 考虑量测时延的数据对齐
由于配网中PMU、AMI 和SCADA 这3 种不同类型的量测在数据精度、数据成分、时标信息和采集频率等方面各有差异,所以在进行数据融合处理时需要选择时标信息较为精确的数据源作为基准,然后将其余类型的数据与基准数据源进行数据对齐,以保证用于状态估计的数据是在同一时间断面下。考虑到PMU 装置是在GPS 时间基准下同步采样,且数据的测量精度为0.05 级,因此以PMU 数据为基准,AMI 和SCADA 数据分别与PMU 数据的时标进行对齐。
1)AMI 与PMU 数据对齐。
安装于用户侧或配变出口侧的AMI 在采集周期下的实时量测会出现不同程度的数据时延,因此不能直接利用AMI 的粗略时标与PMU 量测进行数据对齐。AMI 的采集周期TC=15 min,一天内的采集时刻为00:00、00:15、…、23:45,以有功功率为例,用于t时刻状态估计的负荷有功量测取值公式为
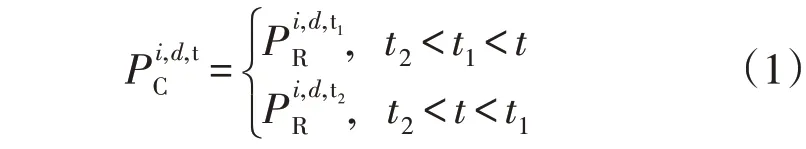
由于通信故障等因素会造成AMI 在t时刻读回的数据丢失,若t时刻无实时有功量测到达,则采用该时刻前1-2 次采集时标的有功量测值参与状态估计。
2)SCADA 与PMU 数据对齐。
由于SCADA 系统接收的远程终端单元(remote terminal unit,RTU)量测数据的时标信息是数据进入数据库的时间而非采集时间,因此,采用对传到主站的PMU 量测数据的时标向后设置一个延迟时间窗的方法,若在时间窗内接收到RTU 数据,则此数据的采样时刻与PMU 数据时刻一致。
设RTU 对应于PMU 采样时刻TA的数据到达主站的时间范围为τw,则量测时延τ服从[tmin,tmax]均匀分布时,τw在[TA+tmin,TA+tmax]上服从均匀分布。设RTU 量测时延的期望值为E(dx),则该量测x的取用时刻公式为

即从TA时刻起等待E(dx)时间后,再从数据库中取用量测x用于状态估计,同时量测的时延期望值被校正为0。
1.1.2 通过插值补全混合量测
在上一小节进行数据对齐的基础上,由于PMU、RTU 和AMI 的采集周期分别为10 ms、2~5 s、15min,即PMU 的量测数据更新速率快,而AMI 和RTU 的量测数据更新速率慢,在以PMU 数据的时间断面为基准的情况下,大量时间断面没有AMI 和RTU 的量测数据与之对应。因此,需要通过插值以补全AMI 和RTU 的量测数据,提高用于配电网状态估计的混合量测数据的冗余度。
根据已知每个采样周期下AMI 和RTU 量测数据的时间断面,采用线性内插法[19]补全每两个时间断面间的量测值可以保证融合后的数据精度。见图1,利用z1和z2可以补全z1和z2之间任意时刻的数据。
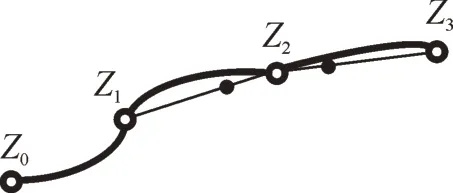
图1 内插法示意图Fig.1 Schematic diagram of interpolation
1.2 改进WLAV抗差状态估计模型
WLAV 抗差状态估计的估计准则是以残差的加权绝对值之和最小为目标,其模型公式为
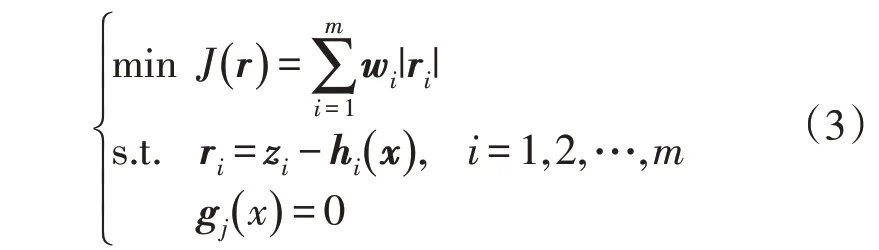
式中:w为权系数向量,一般取为第i个量测误差的方差;ri、zi、h(ix)分别为节点i的残差向量、量测向量、量测函数向量;g(jx)为节点j的零注入函数向量;x为状态量向量。
为消除目标函数中的绝对值量,添加正实数的松弛变量l、u,则WLAV 抗差估计模型化为
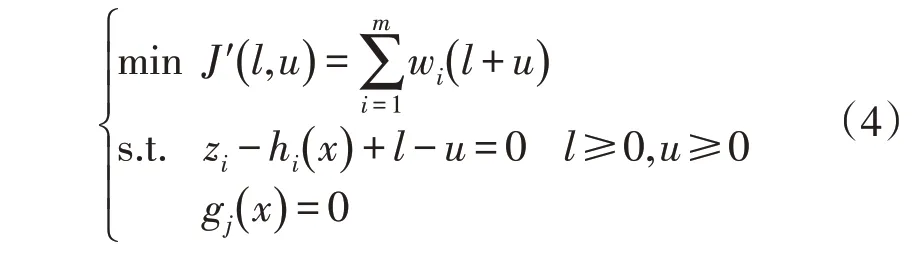
式中,l、u均为m维松弛变量。
引入多源数据融合的配电网混合量测数据后,可以在一定程度上解决WLAV 模型在杠杆点因收敛性不好而求解失败的问题,则改进WLAV 抗差状态估计模型公式为
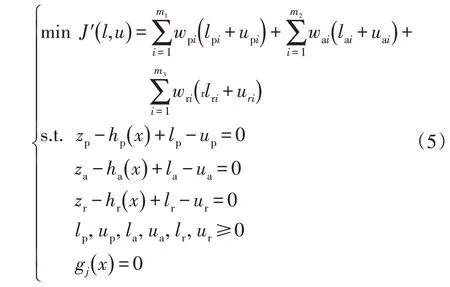
式中:m1、m2、m3分别为PMU、AMI、RTU 量测数据的个数;约束条件中包括节点电压约束、节点注入功率约束和支路功率约束。该模型是一个含有等式约束和不等式约束的非线性优化问题,采用非线性高阶内点法[20]进行求解。
2 站-线-变-户运行状态指标体系
本节通过采用上一小节中抗差状态估计的结果作为数据基础,分别构建变电站、馈线、配变和用户的指标,以反映配电网各层级的运行状态。
2.1 变电站指标
2.1.1 电压偏差离散系数
假设在单位时间内变电站第i条10 kV 母线的运行电压测量值共有n_U个,并将数据点编号记为j,记电压偏差的平均值为δUˉi、标准差为sδUi,则电压偏差的标准差与其平均值之比为变电站内10 kV母线的电压偏差离散系数公式为
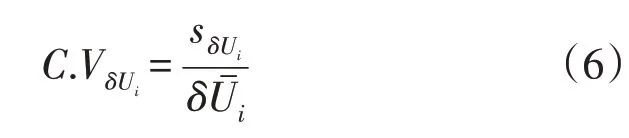
2.1.2 电压越限频次占比
假设在单位时间内变电站第i条10 kV 母线的运行电压测量值共有n_U个,并将数据点编号记为j,记合格电压的上限值为UH、下限值为UL,则电压估计值超过合格电压限值的次数nout与总测量次数n的比值百分比为变电站内10 kV 母线的电压越限频次占比公式为

式中nout根据分类函数来计算,公式为

类似地,可计算电压越上限频次占比和电压越下限频次占比公式为
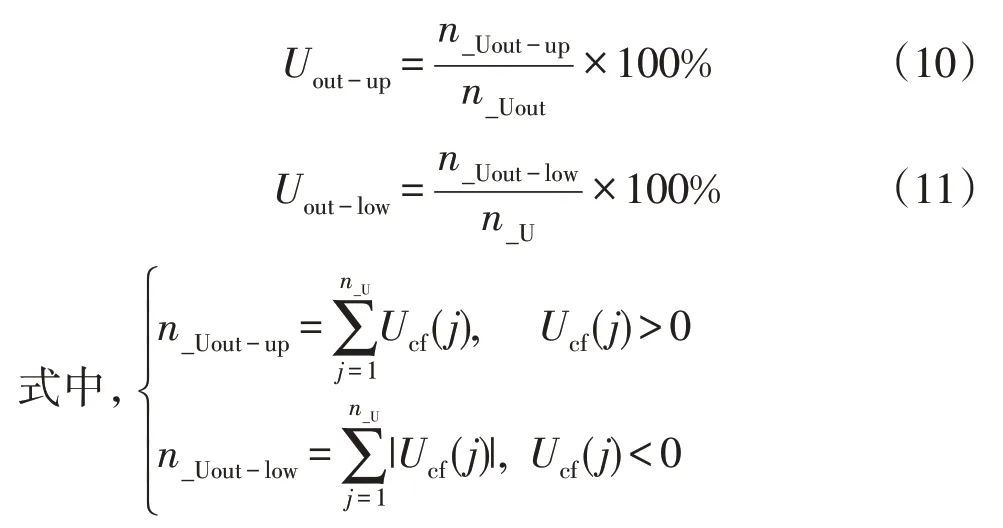
2.2 馈线指标
2.2.1 负载率分布情况占比
假设在单位时间内流过第i条支路的电流测量值共有n_I个,并将数据点编号记为j,记支路i的额定电流为IiN,则支路i的轻载率、重载率和过载率的统计次数分别与总测量数的百分比为负载率分布情况占比公式为
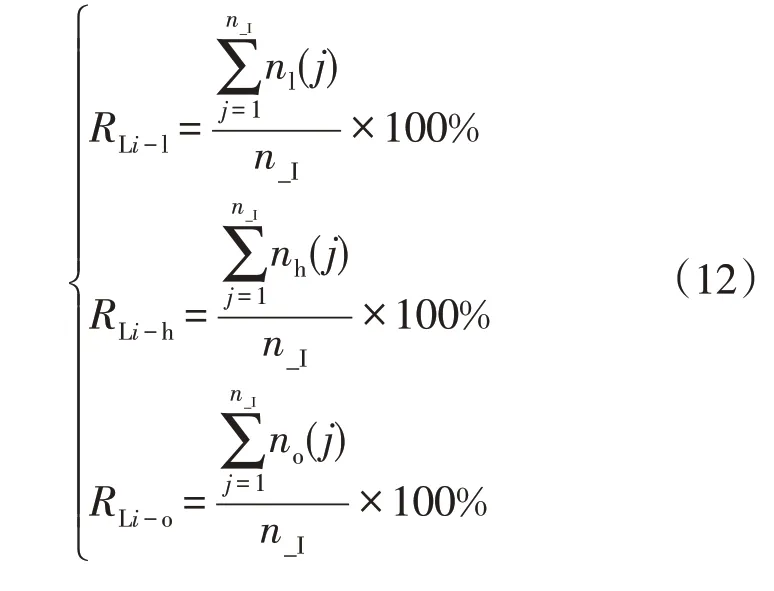
式中:nl(j)、nh(j)和no(j)是由0、1 元素组成的n维向量;对于流过支路i的电流估计值为Ies-i(j),则其负载率:若在[0,20%]区间内nl(j)取1 否则取0、若在[80%,100%]区间内nh(j)取1 否则取0、若>100%则no(j)取1 否则取0。
2.2.2 线损率分布频次占比
假设在较长时间尺度如24 h 内m条线路中流过第i条支路的有功功率测量次数为n_P,并将数据点编号记为j,记支路i首端传输的有功功率估计值为Pes-i、有功损耗为ΔPi,则重损耗支路的频次占比和非重损耗支路的频次占比为线损率分布频次占比公式为
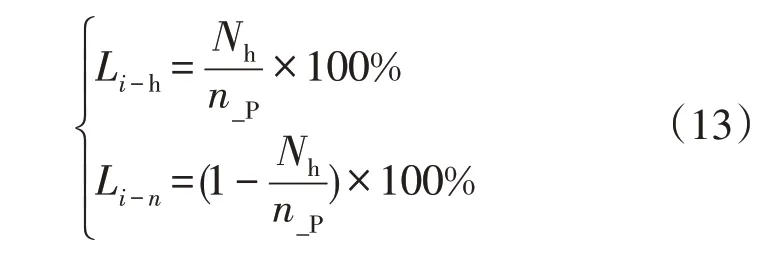
2.3 配变指标
2.3.1 三相不平衡度情况占比
假设在较长时间尺度如24 h 内m台配电变压器中第i台配变的三相电流测量次数为n_Ip,并将数据点编号记为j,记配变i的最大相电流为Ii-max、最小相电流为Ii-min,则轻微三相不平衡度的配变比例和严重三相不平衡度的配变比例为三相不平衡度情况占比公式为
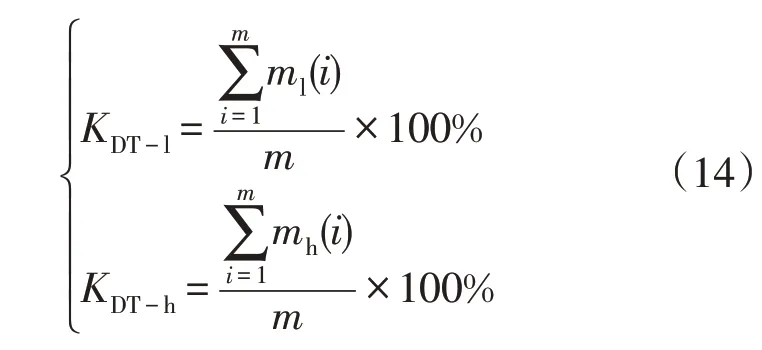
式中:ml(i)、mh(i)是由0、1 元素组成的m维向量,对于配变i的三相不平衡度若在[15%,50%)区间内且时间占比大于5%,则ml(i)取1 否则取0,若≥50% 且时间占比大于20%则mh(i)取1 否则取0。
2.3.2 功率因数合格情况占比
假设在较长时间尺度如24 h 内m台配电变压器中第i台配变的有功功率和无功功率测量次数均为n_P,并将数据点编号记为j,记配变i的有功功率估计值为Pes-i,无功功率估计值为Qes-i,则配电变压器i的合格功率因数、不合格功率因数的统计次数与测量次数的百分比为功率因数合格情况占比。
公式为

2.3.3 电压越限频次占比
根据2.1 节中变电站指标可类似地定义单位时间内配电变压器的电压越限频次占比公式为
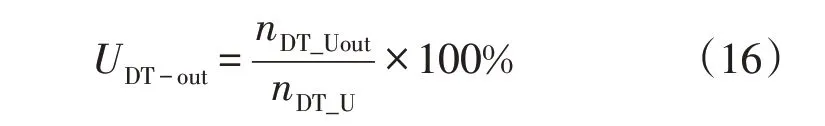
2.3.4 负载率分布情况占比
假设在单位时间内第i台配电变压器首端的有功功率和无功功率测量次数均为n_P,并将数据点编号记为j,记配电变压器i的额定容量为SiN,则配电变压器i的轻载率、重载率和过载率的统计次数分别与测量次数的百分比为负载率分布情况占比。
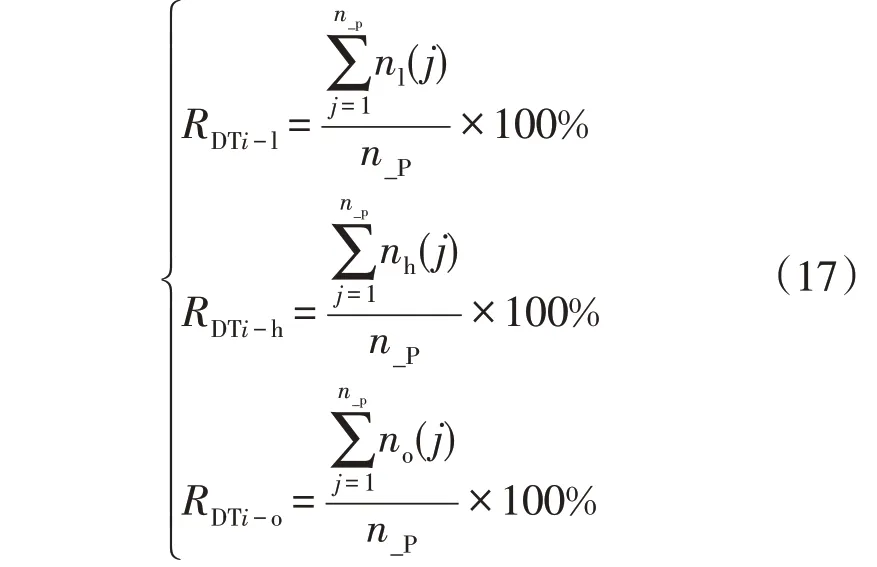
式中:nl(j)、nh(j)和no(j)是由0、1元素组成的n维向量,对于配变i的负载率若在[0,20%] 区间内,nl(j) 取1 否则取0、若在[80%,100%] 区间内,nh(j) 取1 否则取0、若大于100%,则no(j)取1 否则取0。
2.4 用户指标
2.4.1 电压偏差离散系数
根据2.1 节中变电站指标类似地可定义用户的电压偏差离散系数公式为

2.4.2 电压越限频次占比
根据2.1 节中变电站指标类似地可定义用户的电压越限频次占比公式为

本文所提的“站-线-变-户”运行状态指标体系是对不同层级考核的指标进行统计分析,变电站10 kV 母线的指标体现配电网整体的电压水平,馈线指标体现支路是否存在重载/重损情况,配变指标体现负荷水平,用户指标体现台区内用户用电感知最敏感的电压质量。根据该指标体系中不同层级指标的差异性,即可区分配电网不同的站、线、变、户特征。
3 配电网运行状态诊断分析
当前用于配电网诊断分析的数据基础是配电网的原始数据信息[21-28],由于未考虑数据质量问题,所反映的运行状态不准确进而影响诊断结果。因此,本文将抗差状态估计结果用于“站-线-变-户”运行状态指标计算,降低量测误差和坏数据对配电网运行状态诊断分析的影响。本节采用Delphi-CRITIC 法根据各层级的指标计算风险值,定量评估配电网的运行状态;以发现配电网运行的薄弱环节,进而给出各层级运行状态的诊断方案。
3.1 运行状态评估
采用风险分析矩阵法[21]将配电网各层级的运行风险等级划分为1-3,并与风险值区间、风险描述和状态安全级别一一对应,见表1。
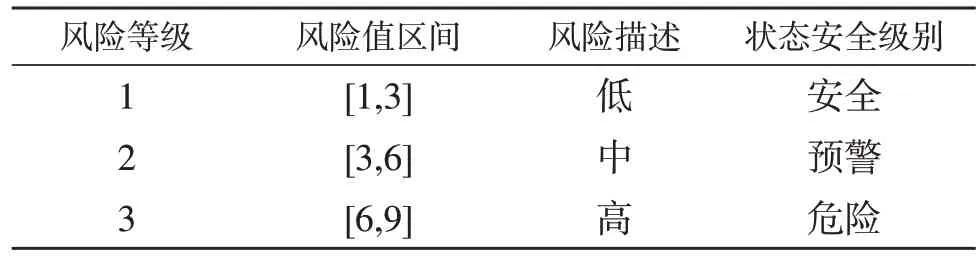
表1 配电网运行状态安全级别划分Table 1 Classification of security levels of operation state of distribution network
首先,应用Delphi 法即专家打分法,专家根据自身的实践经验和指标所反映的运行状态打出相应的分值,其打分范围与表1 中的风险值区间相同,将指标i的分值公式为
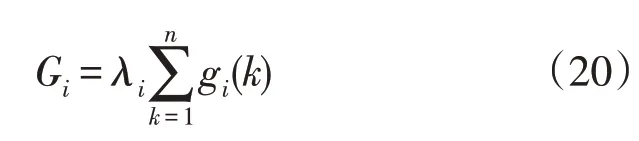
式中:λi为指标i的综合权重值;gi(k)为第k位专家对指标i打出的分值。
综合权重值由主观因子和客观因子共同确定,其中主观因子η根据文献[22]的量化依据计算得到;客观因子ξ的计算采用CRITIC 赋权法[12],该方法同时考虑了指标的变异性(即差异性)和冲突性对权重系数的影响。计算公式为

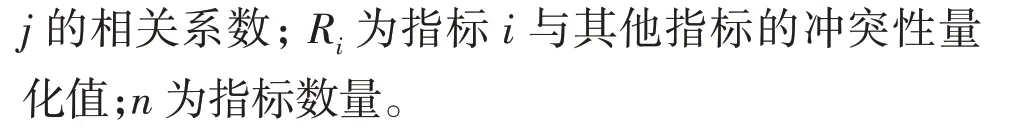
这里为使综合权重λi不偏重ηi和ξi中的任意一项,选用最小二乘法对主观因子和客观因子进行组合优化,目标函数和约束条件公式为
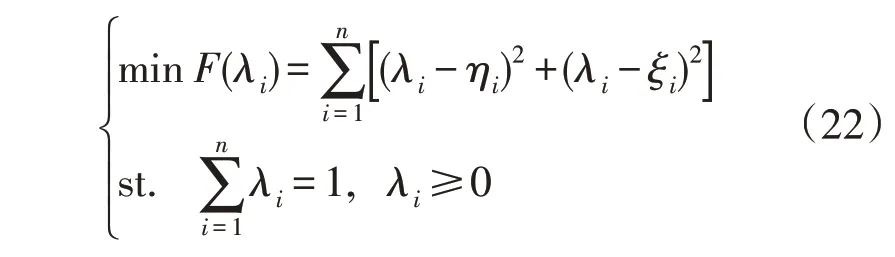
使用拉格朗日乘数法求解即可得到指标i的综合权重值。
3.2 诊断方案
若指标评估值大于阈值6(根据表1 中运行状态安全级别对应的风险值区间),则表征该层级的运行状态存在高运行风险,进而给出相应的诊断方案,见图2。
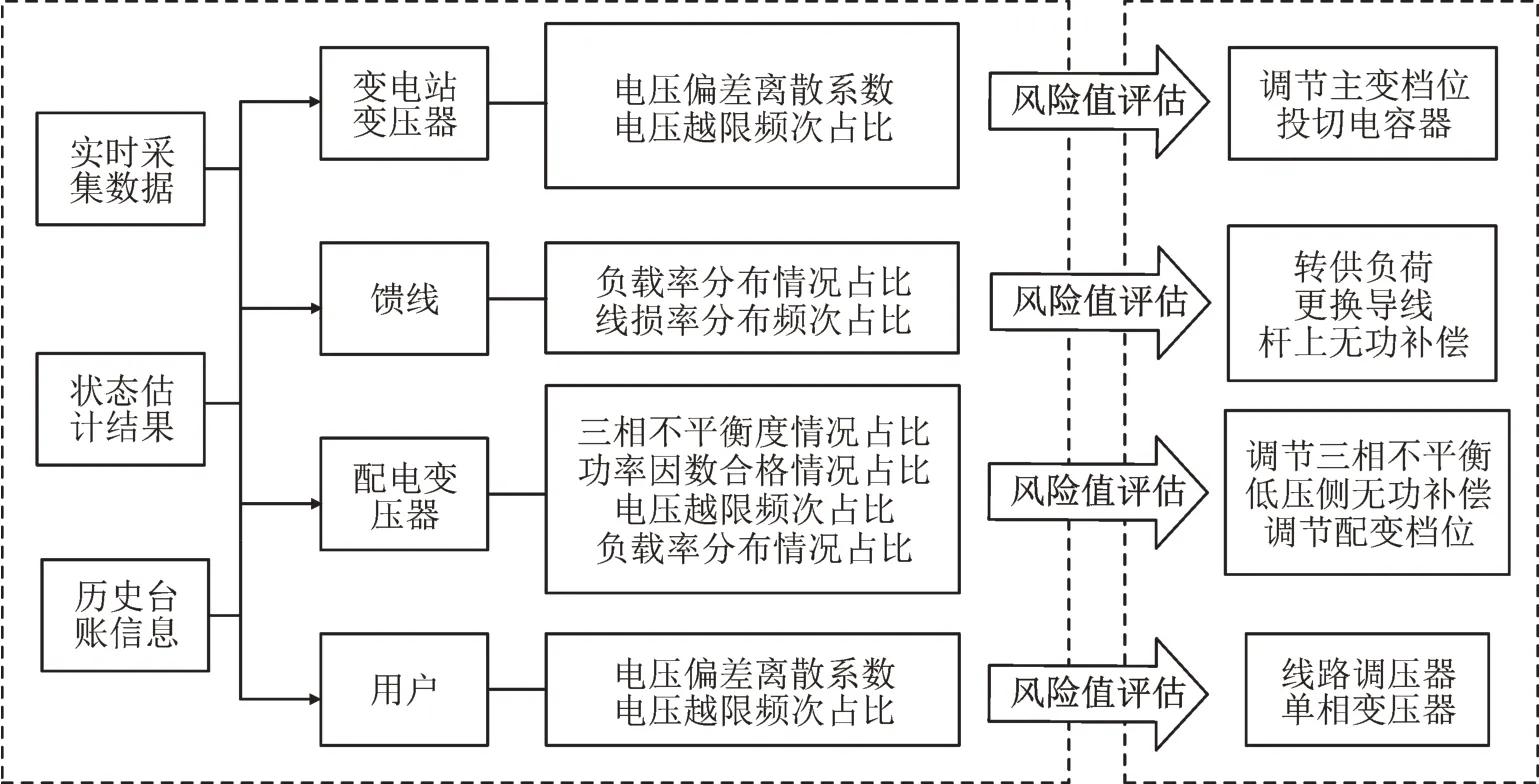
图2 配电网运行状态诊断方案Fig.2 Diagnosis plan for the operation state of distribution network
1)变电站指标风险评估:若变电站的指标表征变电站存在高运行风险,则给出调节变电站主变档位、投切母线并联电容器组的诊断方案。
2)馈线指标风险评估:若馈线的指标表征馈线存在高运行风险,则给出转供负荷、更换高损耗导线或投切杆上无功补偿的诊断方案。
3)配变指标风险评估:若配电变压器的指标表征配变存在高运行风险,则给出加装三相不平衡调节装置、投切配变低压侧无功补偿装置、调节配变档位或更换高损耗配变的诊断方案。
4)用户指标风险评估:若用户的指标表征用户用电存在高风险,则给出在低压线路加装单相变压器、串联线路调压器、更换截面偏小或老化的导线、更改迂回供电的路径、切割负荷到临近配变供电或在用户侧装设光伏或储能的诊断方案。
4 算例分析
为验证本文方法的有效性,在Matlab 中对广东某农村配电线路进行算例仿真分析,图3 所示为F16 线35 节点配电系统,其中位于线路末端的节点为分布式小水电。
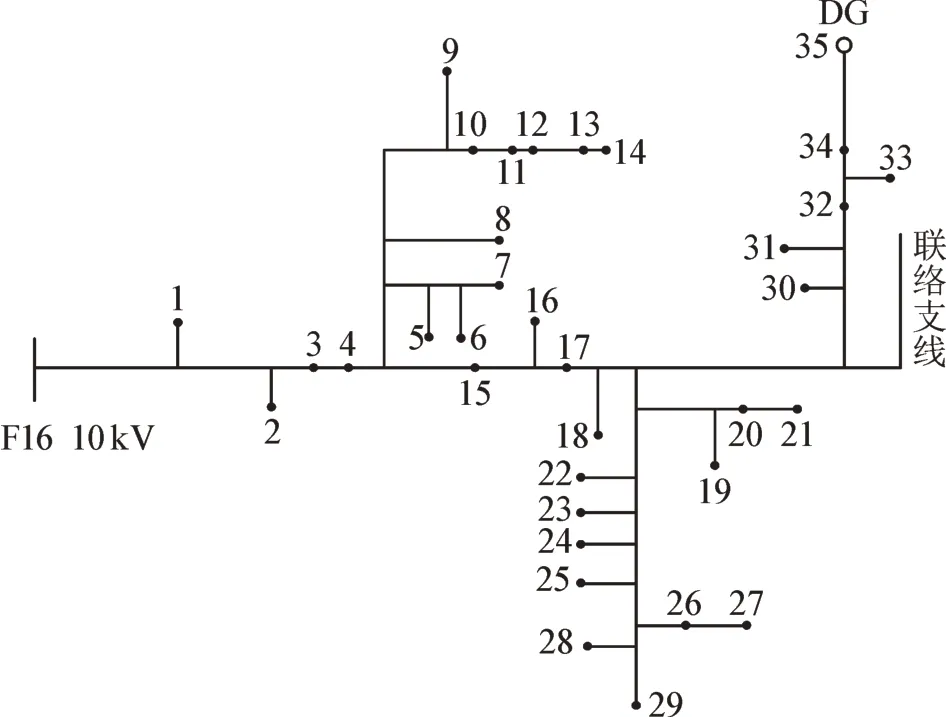
图3 F16线35节点配电系统Fig.3 Distribution system of F16 line 35 node
将收集的F16 线在2019 年8 月12 日的运行数据作为量测向量,由于节点6 在23:45、节点32在8:00 时间断面下的运行数据缺失为0,则为坏数据。将变电站首端母线的运行数据作为PMU 量测,
10 kV 馈线重要节点的运行数据作为RTU 量测,配变计量点的运行数据作为AMI 量测。采用本文方法进行多源数据融合后,代入改进WLAV 抗差状态估计模型,求解结果中电压估计值与电压运行数据(以节点5、17、32 为例)一天的曲线见图4。
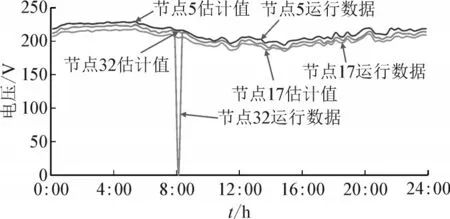
图4 抗差状态估计值与运行数据对比曲线Fig.4 Comparison curve of robustness state estimation value and operation data
可以看出,节点5 和17 的电压估计值与电压运行数据的曲线基本重合,而节点32 在8:00 的电压运行数据为0,电压估计值为214 V,即抗差状态估计可将坏数据异常值修正为正常值,有效提高数据质量。
在IEEE 14 节点系统上,通过对PMU、AMI 和RTU 的量测量总共设置7 个坏数据,对比分析本文方法与文献[17]中抗差状态估计方法的估计精度,见表2。
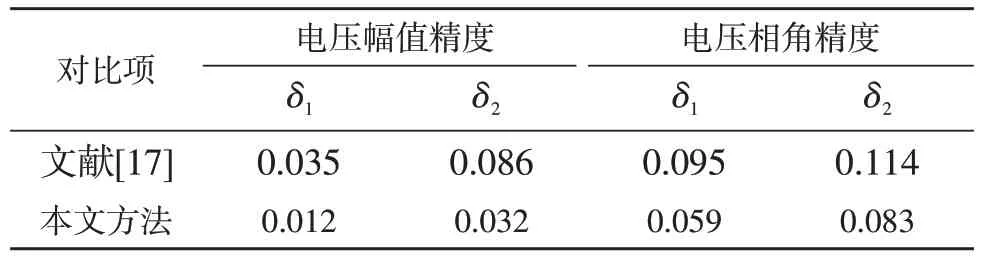
表2 抗差状态估计精度对比分析Table 2 Comparation and analysis of robust state estimation accuracy
其中,平均估计误差δ1衡量坏数据对估计精度的整体影响,最大估计误差δ2衡量坏数据对估计精度的局部影响。从表2 中可以看出,本文方法的估计精度优于文献[17]。
4.1 运行状态指标
根据估计结果计算“站-线-变-户”的运行状态指标,其中变电站首端10 kV 母线的电压偏差离散系数的变化趋势见图5,这里将电压偏差离散系数的限值设为0.05,若小于0.05 则电压偏差的离散程度正常,反之则电压偏差的离散程度明显。
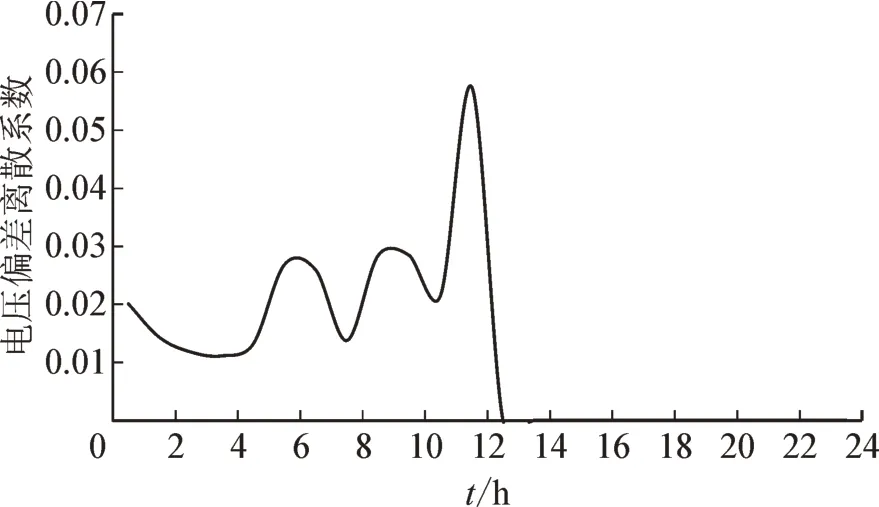
图5 变电站首端10 kV母线的电压偏差离散系数Fig.5 Voltage deviation dispersion coefficient of 10 kV bus at the head of the substation
F16 线各层级的运行状态指标所反映的运行状态如下:
1)变电站。电压偏差离散系数在11 时大于0.05,表明在该单位时间内电压偏差的离散程度明显(调压措施导致);电压越限频次占比为0,则首端母线电压均运行在合格范围内。
2)馈线。根据单线图中的线路型号划分共有74 条线路。负载率分布情况占比中,57 条线路处于全天轻载状态,5 条线路出现轻载运行的频次见表3,其余12 条线路全天正常运行,未出现重过载运行;线损率分布频次占比中,9 条线路出现高线损率的频次见表3,其余线路的线损率均低于设定限值。

表3 馈线运行状态指标Table 3 Operation state indicators of feeder
3)配变。F16 线有35 台配电变压器。三相不平衡度情况占比中,出现轻微三相不平衡的配变比例为88.57%,出现严重三相不平衡的配变比例为85.71%,即配变在不同时段的三相不平衡程度有所变化。
功率因数合格情况占比中,16 台配变的功率因数全天合格,其余19 台配变功率因数出现不合格的时间占比见图6,其中线路末端的小水电全天功率因数不合格。
电压越限频次占比中,仅2 台配变的电压越限频次为0,1 台配变的电压越上限频次为42.71%,其余32 台配变的电压越下限频次见图7,其中有3台配变的电压处于全天越下限,包括线路末端的小水电。
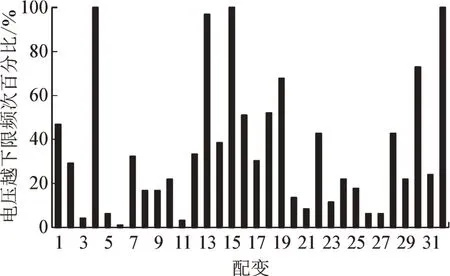
图7 配变电压越下限频次占比Fig.7 Frequency proportion of distribution transformer voltage exceeding the lower limit
负载率分布情况占比中,仅2 台配变的负载率处于最佳运行状态,13 台配变处于全天轻载状态,其余20 台配变出现轻载运行的频次见图8。
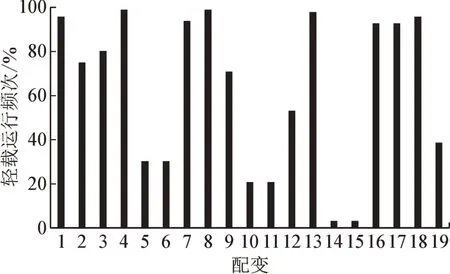
图8 配变出现轻载运行的频次Fig.8 Frequency of light load operation of distribution transformer
4)用户。由于低压台区内用户的电压监测点未全面覆盖,这里用配变首端的电压偏差离散系数来表示台区内用户的电压偏差离散程度,则34 台配变(除线路末端的小水电)电压偏差离散系数大于0.05 的频次即用户电压偏差的离散程度见图9;同样配变电压越限频次占比在一定程度上反映用户电压的越限情况。
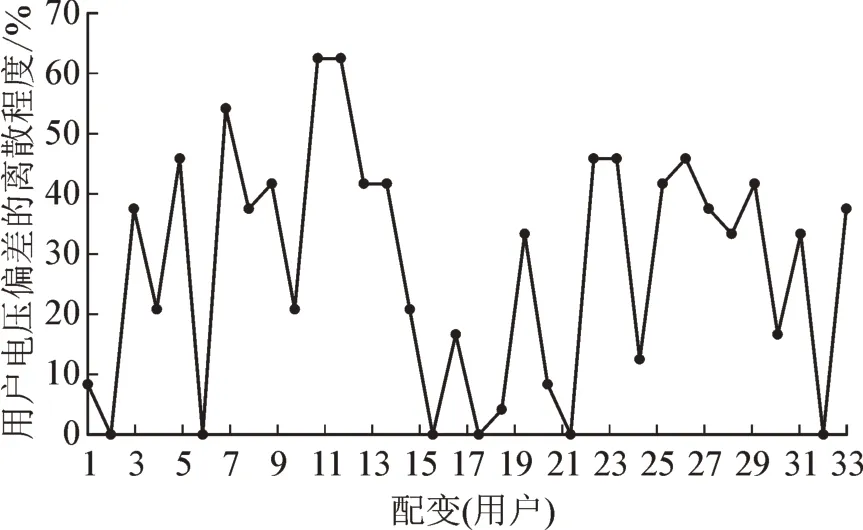
图9 用户电压偏差的离散程度Fig.9 Dispersion degree of user voltage deviation
4.2 运行状态诊断分析
由于本文构建的“站-线-变-户”运行状态指标体系着重于反映各层级的运行状态,现有文献的综合评估指标体系是评估配电网整体的运行状态。故根据前述Delphi-CRITIC 法确定的运行状态指标分值及状态安全级别见表4,将本文方法与文献[11]中AHP-Delphi 法的评估结果进行对比分析,见表5。
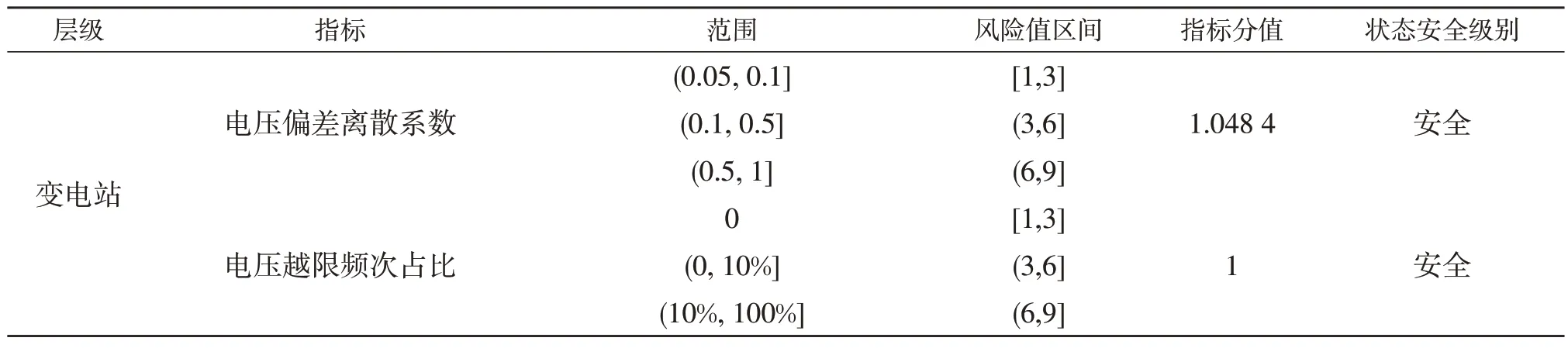
表4 运行状态指标分值Table 4 Indicator score of operation state
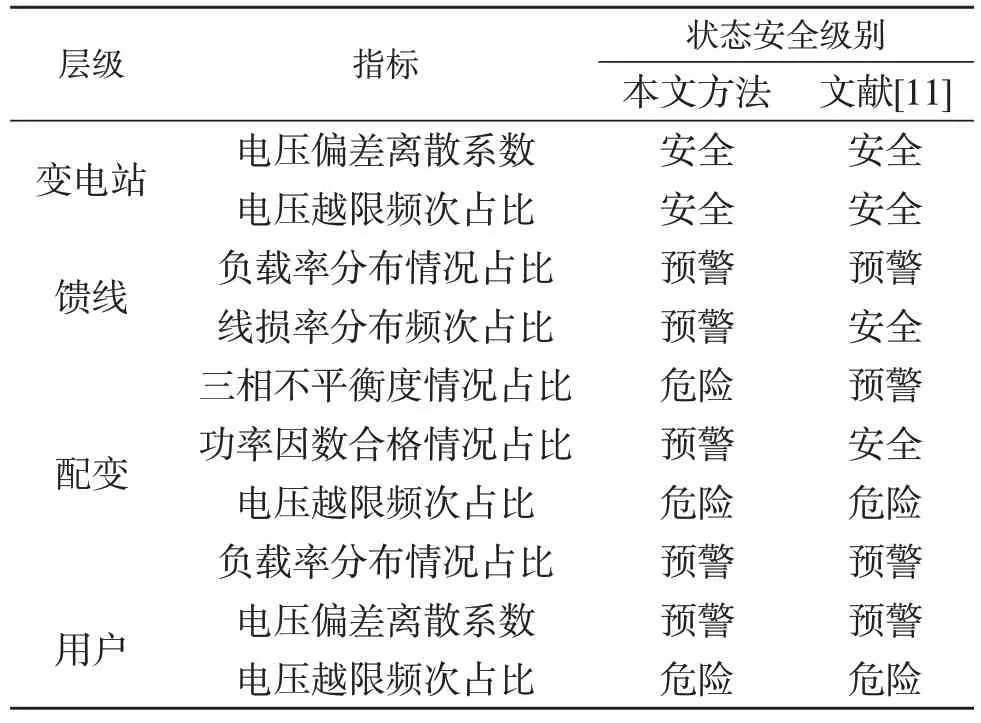
表5 F16线运行状态评估对比分析Table 5 Comparation and analysis of operation state evaluation of F16 line
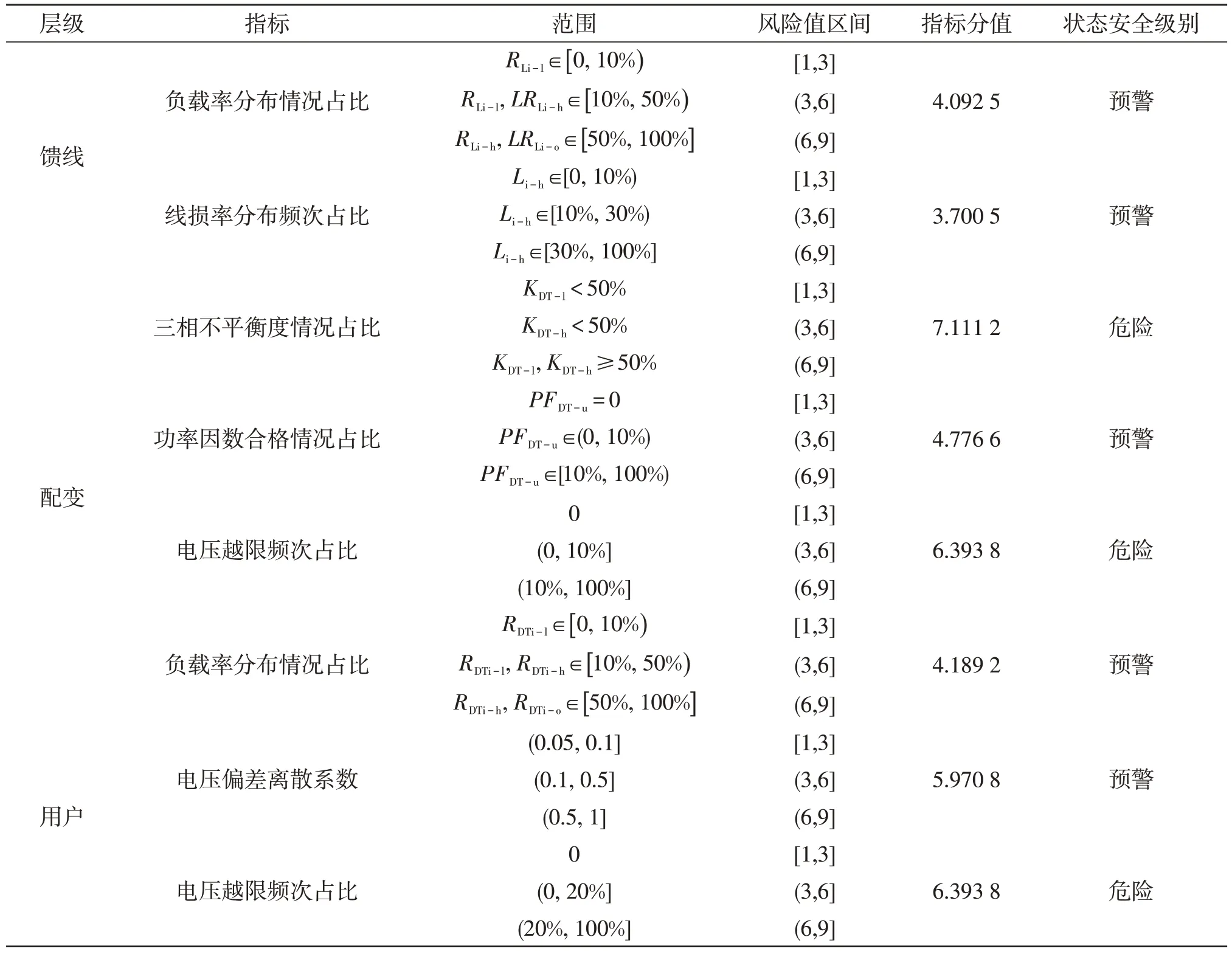
续表
可以看出文献[11]方法受主观影响导致不能准确评估馈线和配变的运行状态;本文方法评估出F16 线存在的运行风险主要存在配变及其低压用户层面,具体为:配变首端的三相不平衡及电压越下限问题突出,配变部分时段的功率因数不合格,配变普遍处于轻载运行状态;用户电压偏差的离散程度明显,且电压越下限严重。
进一步分析出现以上运行风险的原因:首先,农村配电网的供电半径偏长、负荷轻且分散;其次,中压主干线路缺乏大量容性无功;此外,小水电的输出功率小于并网点附近的负荷功率,造成线路末端电压更低。虽然变电站首端母线电压合格,但电压水平较低且沿线电压损耗较大,故配变及其台区内用户的电压普遍越下限。据此,给出各层级的诊断方案见表6。

表6 F16线各层级诊断方案Table 6 Diagnosis plan for each level of F16 line
此外,还可以利用接入中压馈线末端的小水电站调节励磁的能力来改善其并网点及其附近馈线区域的电压水平。
将本文方法与文献[10]的故障诊断方法进行对比分析,见表7。
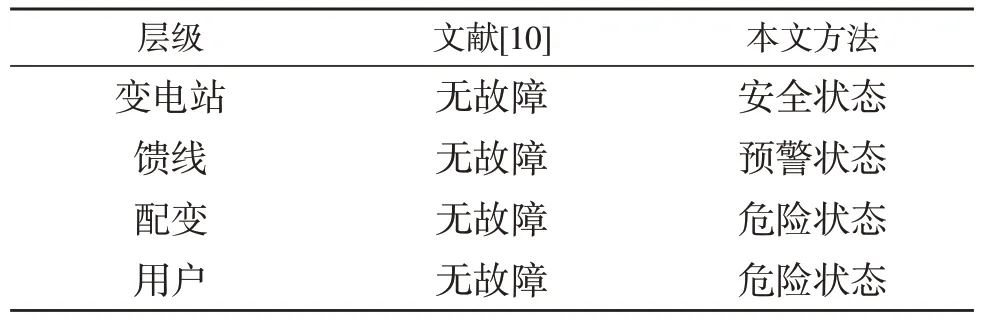
表7 故障诊断对比分析Table 7 Comparison and analysis of fault diagnosis
由于文献[10]是根据保护装置动作及故障记录索引进行配电网的故障诊断,仅适用于已发生的状态。对于F16 线存在运行风险的配电网,相较于文献[10]给出无故障的诊断结果,本文方法可以根据配电网各层级的运行状态安全级别给出相应的诊断方案,以降低故障发生的概率。
5 结语
1)本文将实际配电网的原始数据进行多源数据融合处理后用于抗差状态估计,解决了因通信导致数据缺失而影响运行状态指标准确性的问题。
2)本文采用Delphi-CRITIC 方法确定“站-线-变-户”运行状态指标的综合权重值,可以准确评估配电网各层级的运行状态,进而给出能够有效改善配变及用户电压质量的诊断方案达到降低运行风险的目的。
3)由于电压是影响用户用电感知的直接因素,如何在配电网运行状态诊断分析的基础上,利用“站-线-变-户”各层级的可调节资源解决不同场景下的电压问题是本文下一步的研究重点。
