短舱边界层的稳定性分析及转捩预测

2023-01-05牛萌浩韩宇峰苏彩虹孟晓轩

空气动力学学报 2022年6期

牛萌浩，文豪，韩宇峰，苏彩虹，*，孟晓轩

(1.天津大学机械工程学院，天津 300072；2.西北工业大学航空学院，西安 710072)

0 引言

准确预测边界层的转捩位置是飞行器设计中需要考虑的重要问题。由于湍流边界层表面摩阻显著高于层流边界层[1]，准确预测边界层的转捩位置才能准确计算飞行器的表面阻力。一般来说，民用涡扇发动机短舱阻力占飞机总阻力的5%左右[2]，随着发动机涵道比不断增大，短舱直径也随之增大，短舱表面阻力在全机阻力中所占的比重也明显增加。所以在短舱设计时，希望尽可能优化其外罩型面，使其表面边界层最大程度的层流化，以提升经济性[3-4]。因此，准确预测短舱表面边界层的转捩位置对于短舱的优化设计具有重要意义。

目前，可用于工程上的转捩预测方法可主要分为以下三类：（1）基于边界层当地参数关系式的预测方法，例如广泛采用的 Reθ/Me方法[5]；（2）以RANS为基础的转捩模型，如Langtry和Menter等[6-8]提出的γ-Reθt转捩模型；（3）以线性稳定性理论（linear stability theory,LST）为基础的eN方法[9-11]。前两种方法的最大优点是，可以非常方便地植入到CFD求解器中，计算效率高，因而应用广泛。然而，其主要的不足是缺乏对流动物理机制的考虑，需要通过大量实验数据校正模型中所包含的众多参数[12]。第三种方法基于线性稳定性理论，通过计算边界层中不稳定波在线性放大过程中幅值增长的倍数来预测转捩。由于考虑了转捩过程的基本机理，即边界层的不稳定性，eN方法被普遍认为是更准确、更可靠的转捩预测方法[12-17]。但是，由于该方法并不基于局部变量，计算量比前两种方法更大，而且对于复杂外形，在与多块网格并行计算的CFD求解器结合时存在一定的困难。

eN方法在与复杂CFD流场求解器结合时主要存在两个方面的困难[18]。一是，需要CFD求解器提供垂直于物面方向的物理量以确定线性稳定性控制方程（即Orr-Sommerfeld方程）的系数。而一般情况下，求解流场时很难保证法向网格垂直于物面。二是，在应用eN方法时，需要跟随扰动波的传播方向积分增长率。同样，网格线不可能刚好与扰动波传播方向重合。因此，其应用要比仅依赖于当地变量的转捩模式方法复杂得多。但鉴于转捩预测在短舱型面设计中的重要价值，为了获取准确、可靠的转捩预测结果，有些情况下在计算资源上的投资是值得的。

大部分关于短舱转捩的研究都是从自然层流化设计的角度开展，例如文献[19-22]，直接关注短舱转捩预测的工作非常少，有关层流短舱的实验结果也很少。Lin等[23]采用γ-Reθ模型对短舱表面边界层的转捩位置进行预测（马赫数范围为0.8～0.88，攻角从-2°～0°），发现短舱周向大部分区域与实验结果的比较是合理的。杜玺等[2]在德国ETW风洞开展了层流短舱实验，采用TSP方法测量转捩。实验观察到短舱表面存在明显的楔形层流区，猜测是风洞中灰尘杂质带来的影响。尽管无法明确给出转捩线沿短舱周向的分布，但总体来看，马赫数从0.8增加到0.87，短舱层流区面积明显增加；攻角从0°增加到4°，短舱下部（迎风区附近）层流区增加。孟晓轩等[24]分析了短舱转捩的影响因素，但缺乏对短舱边界层稳定性的细致分析。

本文基于线性稳定性理论细致分析短舱边界层的稳定性特征，给出短舱边界层中起主导作用的失稳机制，并采用eN方法给出转捩线的分布，分析攻角、巡航马赫数对转捩的影响规律。目的是为短舱优化设计及开展实验测试提供重要参考。

1 计算模型和流动条件

短舱表面流动状态主要与外罩型线有关，因此，可将短舱的进排气系统简化，且忽略安装构件的影响[25]，得到的通气短舱如图1所示。

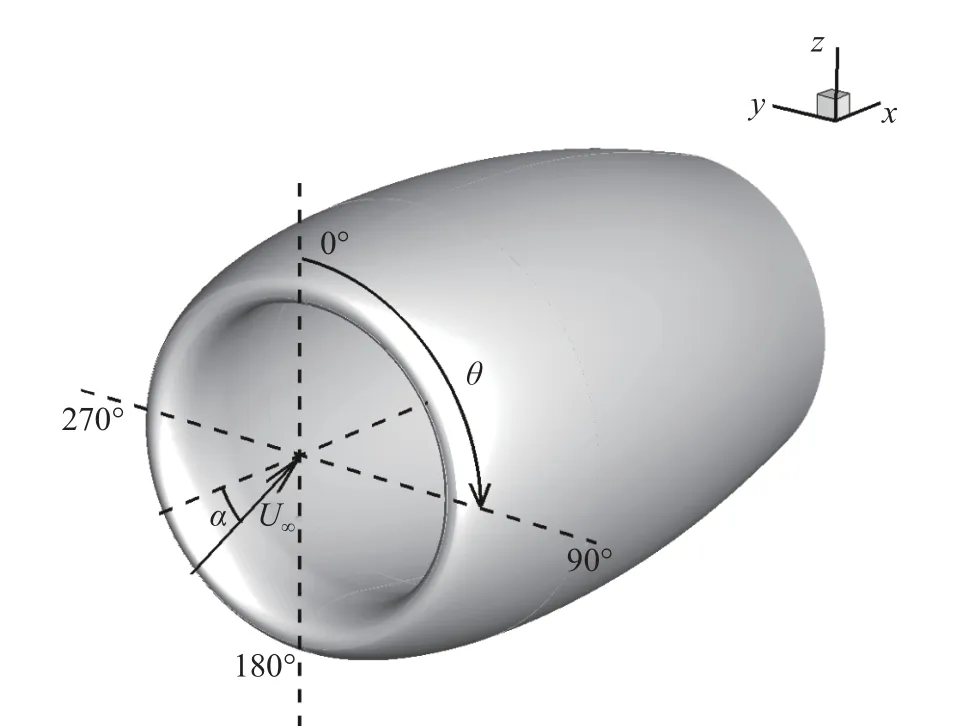
图1 短舱示意图（U∞位于x-z平面内）Fig.1 Schematic diagram of the nacelle (U∞liesin the x-z plane)

短舱的轴向长度为5.5 m，坐标原点位于短舱进气道的中心，x轴沿短舱轴线方向。标记短舱顶部为θ =0°（背风面），底部为θ = 180°（迎风面）。考虑巡航状态下的流动条件，飞行高度为11887 m，来流温度为216.65 K，壁面温度条件为绝热壁，飞行速度为250.8 m/s，以自由来流物理量定义的单位雷诺数为5.58×106/m，侧滑角为0°，来流攻角为5°，马赫数为0.85。在本文第4节中，我们还分析了攻角分别为1°和3°，马赫数分别为0.8和0.89的情况。

2 基于线性稳定性理论的e N方法

高空中的自然转捩是由边界层中不稳定波的持续增长和放大导致的。以线性稳定性理论为基础的eN方法本质上是基于一种模态竞争的思想，即所有可能的小扰动各自独立增长，最先达到预设转捩阈值的扰动就是触发转捩的关键扰动，而其对应的位置就是预测的转捩位置。

根据线性稳定性理论，小扰动可以写成如下的行进波形式：

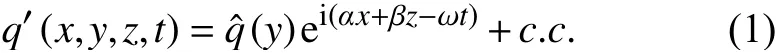
将式（1）代入线性化的N-S方程中，减去平均流满足的方程，得到所谓的Orr-Sommerfeld方程（O-S方程）。对于二维情况，β =0。已知物理量沿法向的分布，给定扰动频率ω，求解O-S方程的特征值问题可以得到不稳定波的波数αr和放大率-αi（αi＜0表示扰动波是增长的）以及特征函数。从扰动开始放大的位置即中性点开始，沿扰动传播方向（二维情况中扰动向下游传播），对不稳定波的放大率积分，可得扰动波的幅值为：

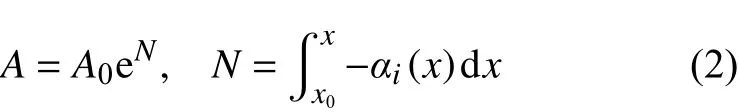
式中，x0为中性点的位置，A0为扰动在中性点处的初始幅值。

对于一般的三维边界层，扰动往往是三维的，采用O-S方程求解β（空间模式中β为复数）时，需要补充额外的条件。由于α、β满足一定的相容关系[26]，可取βi=0。Cebeci和Stewartson[27]通过研究一个波包的演化，采用最速下降法提出一个补充条件：

eN方法需要沿着扰动传播方向对增长率积分，计算幅值的放大倍数。扰动沿群速度Vg的方向传播：

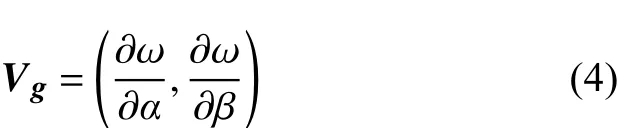
这需要计算时对每个频率在每个积分站位求解群速度方向，再求解O-S方程得到增长率，计算量非常大。一般认为，对于以流向流动为主的情况，扰动群速度方向与边界层外缘的势流方向很接近[28-30]。为了节省计算量，我们沿着无黏流线计算不稳定波的幅值增长。这样，N值由下式给出：

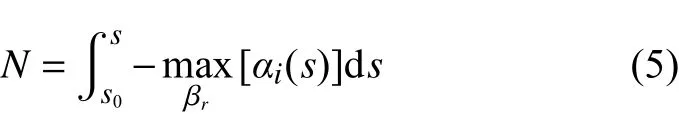
s为无黏流线上的积分站位。假设转捩判据为N = Ncri，不同频率的扰动达到转捩阈值Ncri的位置不同，其中最靠上游的就是预测的转捩位置。Ncri的具体取值需要依赖实验数据和经验确定。

稳定性方程的求解采用天津大学自主开发的SAYR程序，该程序采用四点四阶Malik格式离散O-S方程，采用Muller法求边界层不稳定模态的特征值。目前，该程序已成功应用于从亚声速到高超声速多种构型边界层的稳定性分析中，如后掠翼型[31-32]、超声速平板[33]、高超声速圆锥[34-36]以及组合体外形[37]等。

3 短舱表面边界层的转捩预测

3.1 计算基本流场

在短舱四周和内部构建结构网格，计算域入口和出口距短舱约为26～27个短舱长度。短舱表面的边界层内布置70个左右的网格点，总网格量约为5300万。借助CFD开源程序，利用加速收敛的多重网格技术，采用二阶精度的有限差分法求解RANS方程，得到短舱的基本流场。求解RANS方程时，采用Spalart-Allmaras（S-A）湍流模型，取固定转捩位置为x =3.7 m，此位置之前的流场为层流解，之后采用S-A湍流模式求解。

边界层中T-S波的稳定性受压力梯度的影响。通常情况下，顺压梯度使边界层更稳定；反之，逆压梯度使边界层更不稳定。图2给出了4个周向位置处压力系数沿x的变化。可以看出，在背风面θ = 0°处，只有很短的顺压区，逆压区长度较长，在x =1.6 m附近出现激波。在迎风面θ =180°处，顺压区相对较长，在x = 2.4 m处出现激波。侧面的情况介于两者之间。由于逆压梯度的存在，短舱表面会出现边界层分离。在分离区附近，边界层局部平行性假设不再成立，线性稳定性理论不再适用。因此，我们关注的主要是短舱前半部分，即边界层分离前的流场。

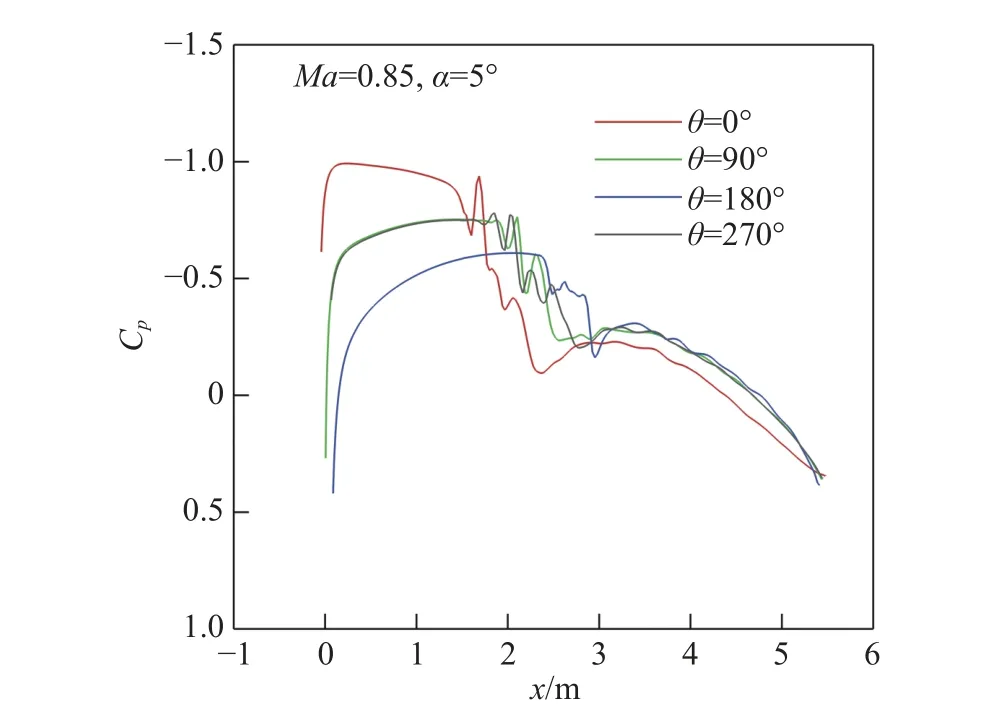
图2 压力系数沿x的分布Fig.2 Variation of the pressure coefficient along x

为了验证流场计算的可靠性，特别是从不同流向位置开始采用S-A模型计算对短舱上游流场的影响，我们将固定转捩位置选在短舱末端，即全场用层流求解，这时计算全部流场需要较长的时间才能收敛。选取激波前的位置，比较层流解和固定转捩位置的层流解加S-A湍流模型所得速度剖面，结果如图3所示。纵坐标η表示垂直于壁面的方向。速度用飞行速度进行无量纲化。可以看出，在激波出现前，边界层剖面是一致的。这表明，在短舱前部，即边界层分离前，固定转捩位置的湍流模式可以给出定常收敛的基本流场，可作为线性稳定性分析的基础。之后的其他工况均采用该方法进行基本流场计算。

为了验证边界层内的网格量是足够的，我们将边界层内的网格从70个增加到130个。图4给出了网格加密前后θ =0°和θ =180°子午面上不同流向位置速度剖面的对比。可以看出，结果吻合很好。这说明，边界层内的网格量是足够的。在之后其他工况的计算中，也采用相同的网格布置。

3.2 获取线性稳定性分析所需的边界层剖面

采用LST进行分析时，需要提供沿壁面法向方向的物理量及导数，以得到O-S方程的系数矩阵。但是，通常CFD的计算网格并不垂直于壁面，为此，需在垂直于壁面方向上重构网格，采用插值的方法得到新网格下的流场信息。

以图5（a）所示的壁面某一位置P(i,k)为例，说明从该点出发提取流场信息的步骤，具体方法可参考文献[38]。i、k分别表示贴体坐标系下的流向和展向指标，网格线单位矢量分别记为ai、ak。

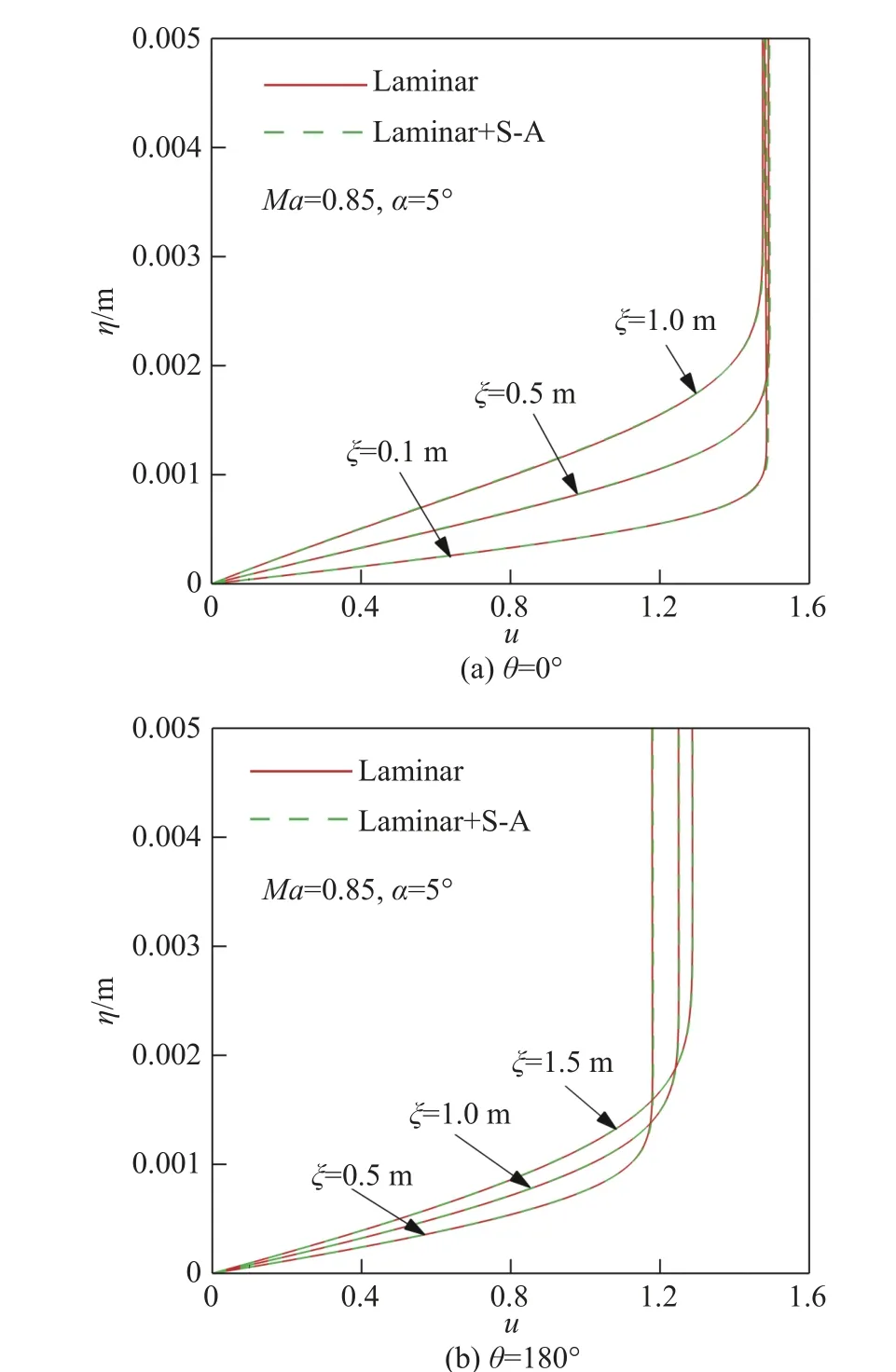
图3 不同计算方法所得流向速度剖面的比较Fig.3 Comparison of streamwise velocity profiles obtained by different methods

（1）求出P点沿壁面法向的单位矢量 aj=ak×ai；

（2）沿着aj方向，以指数型分布布置新网格点，并确保边界层内有足够的点；

（3）采用四点三阶Lagrange插值方法，得到新网格点上的各物理量；

（4）确定边界层外缘处的速度方向，即无黏流线的方向。从P点开始，沿流线方向在壁面网格上插值出下一个积分站位。重复上述步骤，依次向下游推进，最终可得到由无黏流线和壁面法向确定的曲面内的流场，即图5（b）所示新网格上的流场。

3.3 线性稳定性分析

短舱边界层中存在的不稳定模态有T-S波和横流涡，需要分析在转捩中起主导作用的模态。由于横流失稳主要发生在短舱侧面，我们在短舱侧面选取三条典型的流线，分别是从唇口处θ =50°、θ = 90°和θ =120°出发的流线，分别记为Line 1、Line 2和Line 3，如图6所示。在每条流线上选取一个离唇部不远的位置：Q1(0.501 m,-1.303 m,1.180 m)、Q2(0.506 m,-1.751 m,0.112 m)和Q3(0.506 m,-1.564 m,-0.793 m)。将Q1、Q2、Q3处的速度分别投影到无黏流线方向和垂直于流线方向上，得到势流方向的速度分量us和横流速度分量uc。图7（a、b）分别给出了us和uc沿法向的分布。可以发现，横流速度分量很小，不到边界层外缘速度的3%。

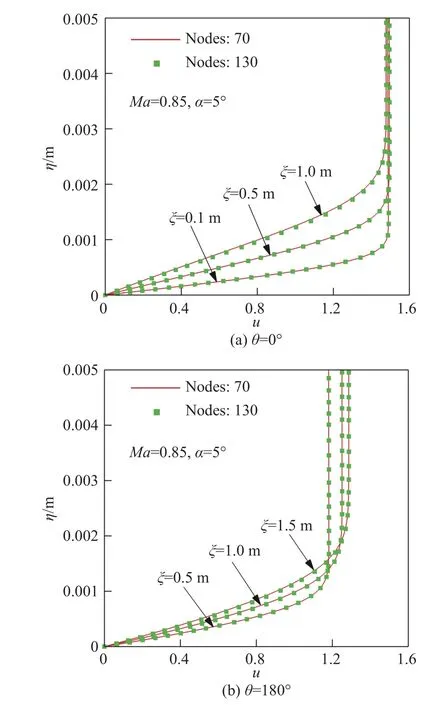
图4 加密前后流向速度剖面的比较（加密的工况只显示了部分网格点）Fig.4 Comparison of streamwise velocity profiles before and after the mesh refinement (only a part of the grid nodes is shown for the denser grid case)

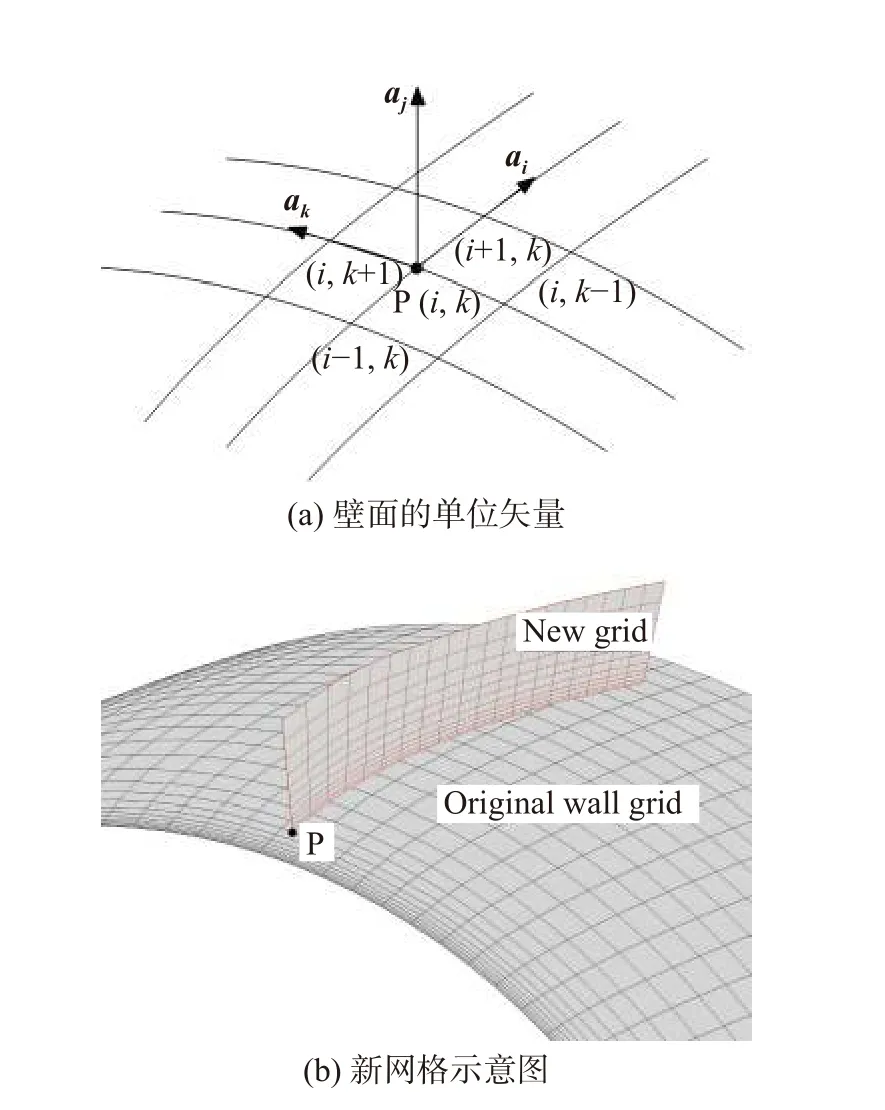
图5 用于线性稳定性分析的新网格Fig.5 New gridsused for the linear stability analysis

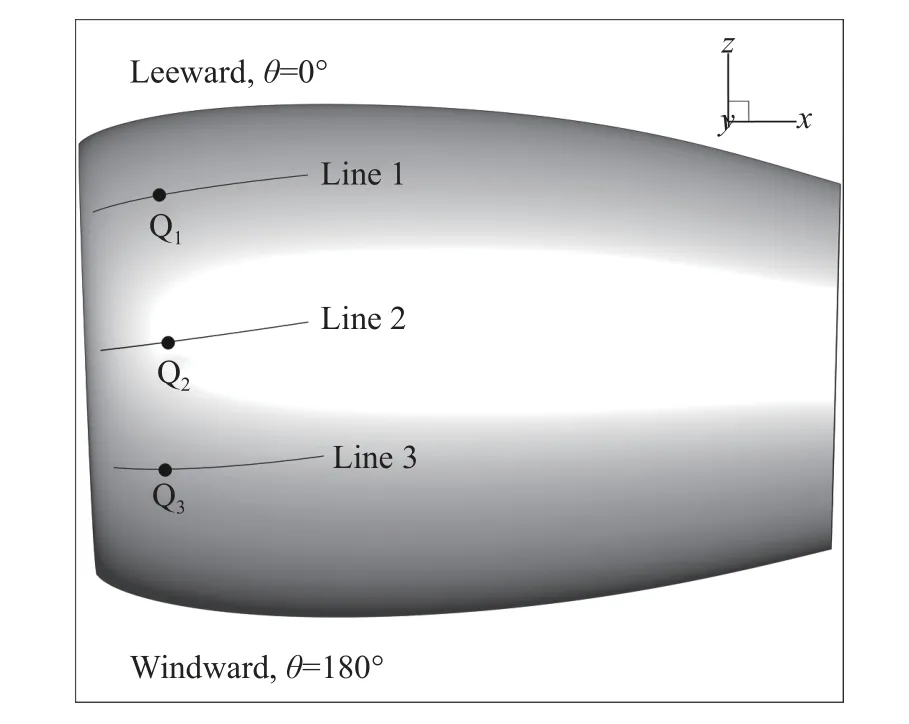
图6 短舱侧面流线Fig.6 Streamlineson the side of the nacelle

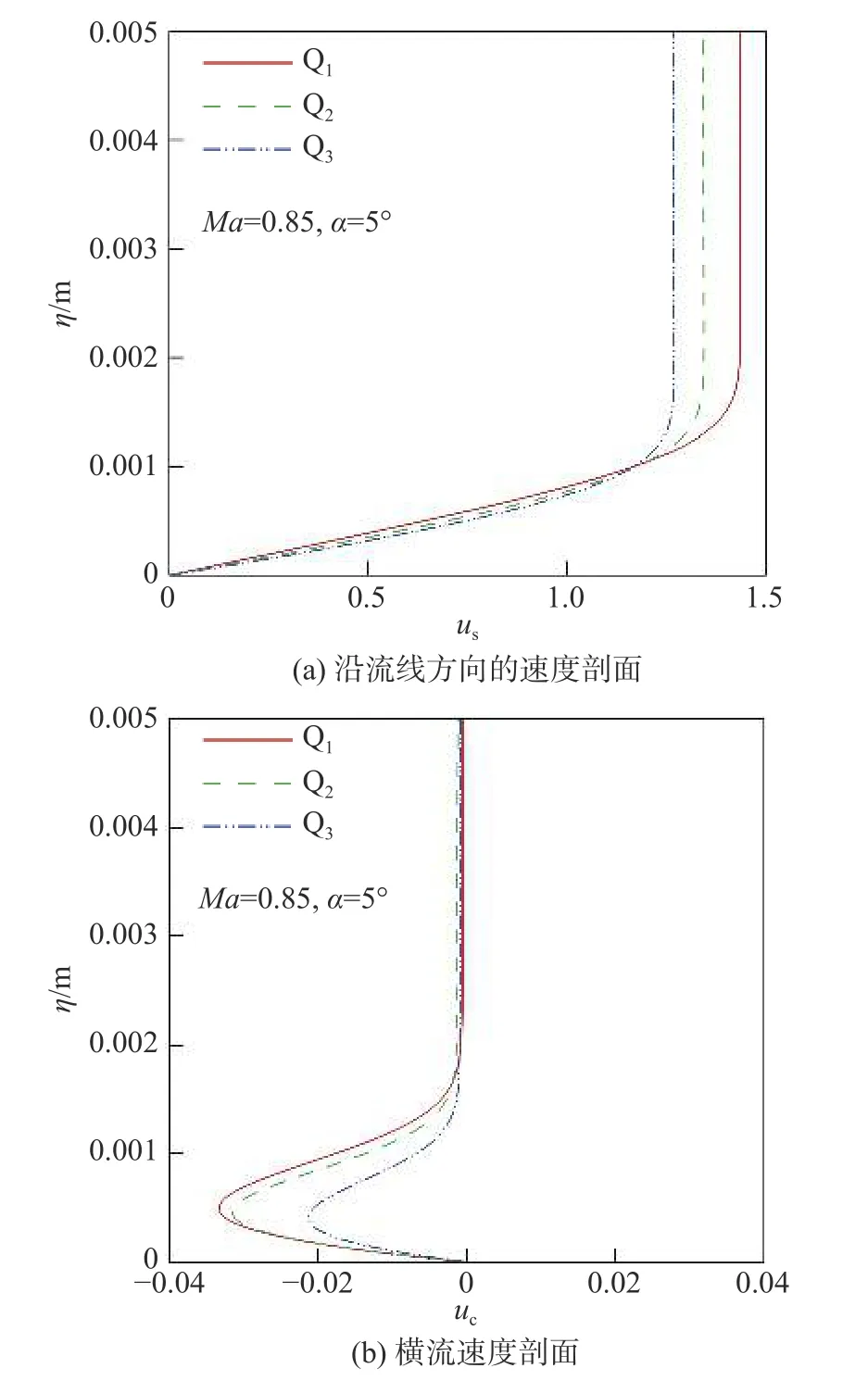
图7 速度剖面Fig.7 Velocity profiles

采用线性稳定性理论计算三条流线上的T-S波和定常横流涡（stationary vortex）的增长率。图8（a～c）分别给出了三条流线上不同频率的T-S波和定常横流涡（频率为0）的增长率沿流向的变化。可以发现，T-S波开始失稳的位置更靠前，且增长率显著大于定常横流涡。利用式（5），从中性点开始沿着无黏流线积分增长率得到N值曲线，结果如图9所示。可见，T-S波的N值显著大于定常横流涡的N值。因此，对于巡航状态下的小攻角情况，T-S波比横流的不稳定性更强，是转捩的主导模态。在之后的转捩预测中，我们只考虑T-S波失稳引起的转捩。

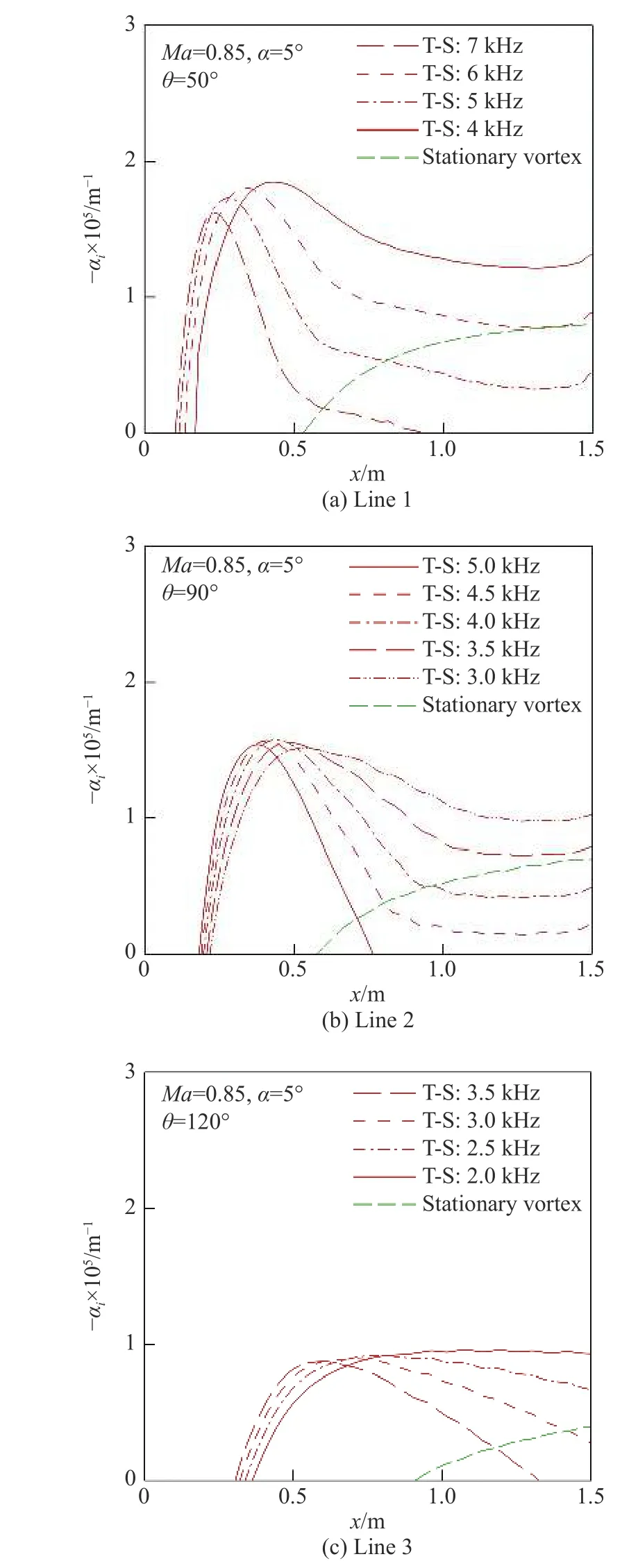
图8 定常横流涡与T-S波增长率的比较Fig.8 Comparison of growth ratesof the stationary crossflow vortex and the T-Swave

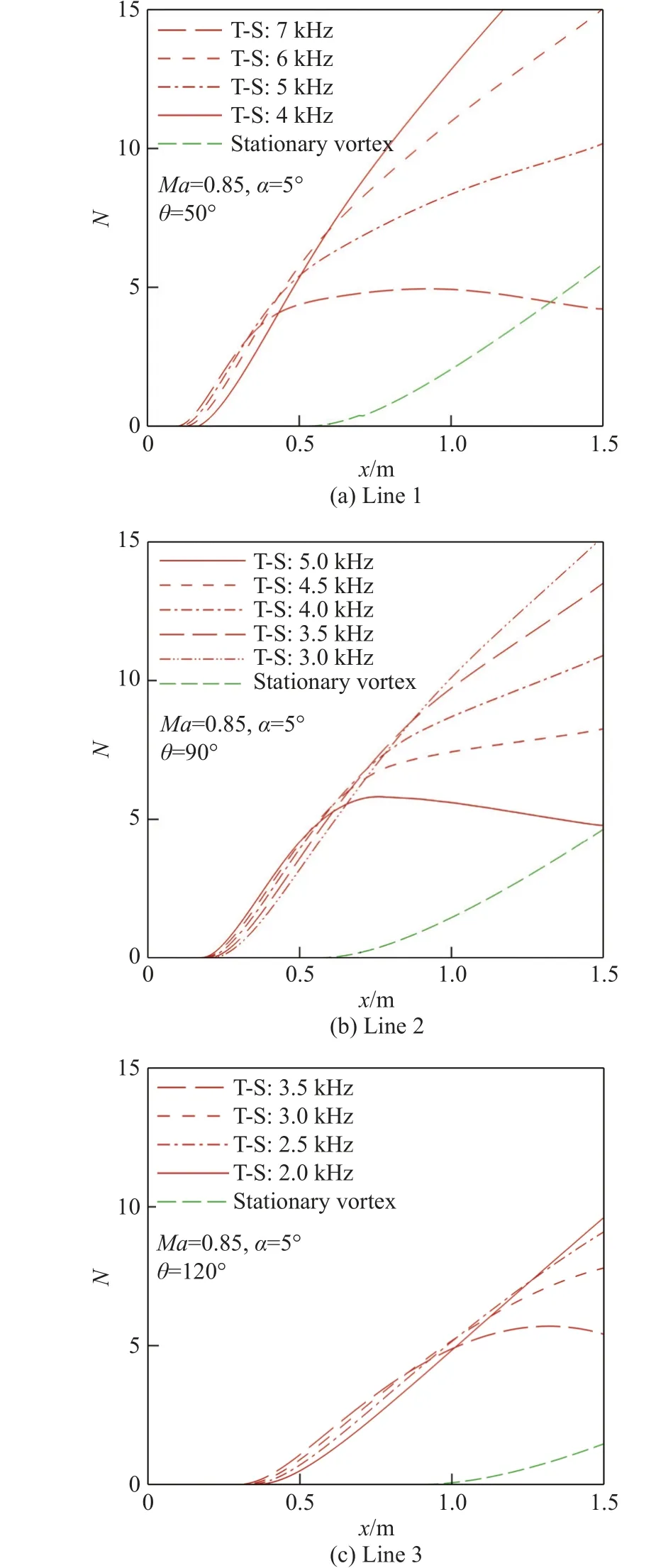
图9 定常横流涡和T-S波积分所得N值的比较Fig.9 Comparison of N factorsof the stationary crossflowvortex and the T-Swave

3.4 结合判据预测转捩位置

前面提到，eN方法中转捩判据的确定需要依赖实验和经验。但对于宽体客机的发动机短舱，雷诺数高达3×107左右，可获得的实验数据很少。并且，由于构型和流动条件与航空翼型显著不同，也无法直接借用翼型常用的转捩判据。例如，Mack[39]曾提出一个与来流湍流度有关的经验的转捩判据，即：

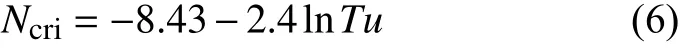
式中，Tu表示来流湍流度。Lin等曾将其用于自然层流化短舱的转捩预测中[23]。然而，由于目前并不清楚实验中湍流度的具体情况，无法给出可靠的Ncri。因此，本文暂时不讨论具体的转捩位置，仅给出不同判据下转捩线的分布。待获得进一步的实验数据后，可标定Ncri值，从而确定最终的转捩位置。

以从θ =90°处出发的流线为例，不同频率T-S波的N值曲线在图9（b）中给出。暂时将转捩阈值Ncri定为5～10的整数，可以得到不同频率T-S波达到转捩阈值对应的位置，如图10所示。对于某一Ncri，最靠上游的位置就是预测的转捩位置，其对应的频率就是该判据下触发转捩的关键频率。可见，随着Ncri增大，转捩位置靠后，关键频率降低。Ncri从5增加到10时，转捩位置从0.57 m推迟至0.99 m，关键频率从4.5 kHz降到2.9 kHz。

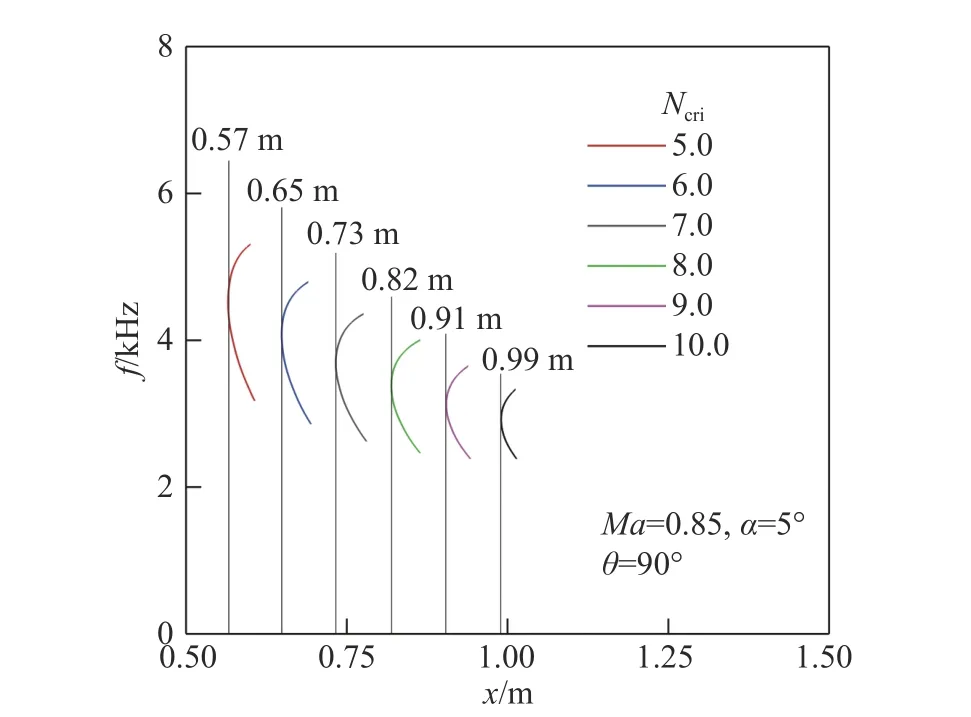
图10 不同频率T-S波对应的转捩位置Fig.10 Transition location for T-S waveswith different frequencies

至此，对于某一转捩阈值Ncri，我们得到了一个转捩点。由于无黏流线并不完全在θ =90°子午面内，因此得到的转捩点也会偏离该子午面。对短舱的其他周向位置都进行类似的分析，可以得到转捩线沿周向角度的分布，结果如图11（a）所示。图11（b）给出了转捩线在短舱上的分布。可见，在θ =0°～90°范围内，转捩位置变化不大，而在θ =90°～180°，即靠近迎风面处，转捩位置随周向角度增加明显后移。迎风面处转捩位置最靠后，而背风面转捩靠前。这与通常认识的小攻角对转捩的影响结果一致[23]。

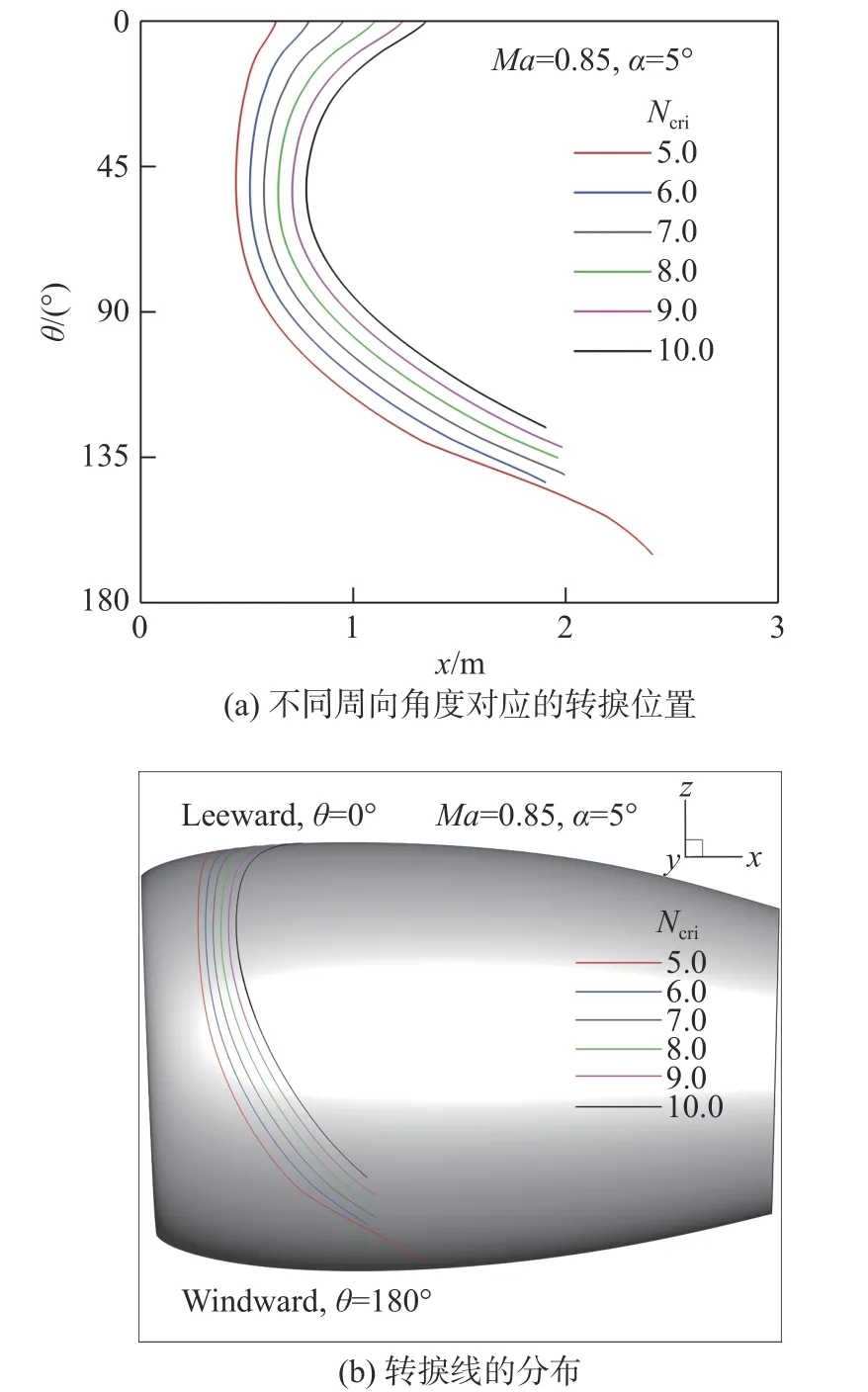
图11 短舱转捩预测结果Fig.11 Transition prediction result for the nacelle

从图11中注意到，当Ncri比较大时，转捩位置在迎风面附近存在空档。为了具体考察迎风面处的流动情况，图12（a）给出了θ =180°子午面上的流线分布。可见，边界层在x =2.4 m处开始分离，壁面附近出现分离泡。图12（b）给出了对应的壁面摩擦系数沿x方向的分布。Cf曲线与x轴的第一个交点代表分离开始的位置，第二个交点代表流动再附的位置，图13给出了不同频率T-S波的N值曲线。前面曾提到，在边界层分离附近，线性稳定性理论不再适用，因此，N值曲线在分离位置附近停止。从图中可以看出，转捩阈值Ncri大于5时，T-S波无法达到给定的转捩阈值。因此，图11（a、b）所示的转捩线在迎风面存在空档。

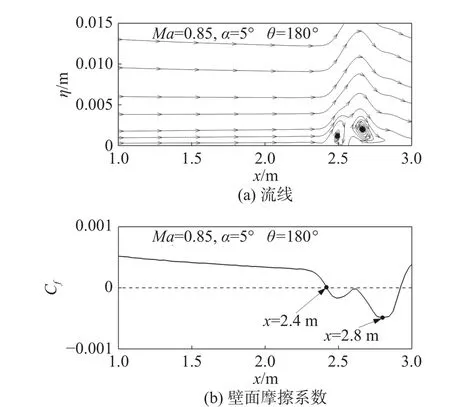
图12 迎风面处的流线和壁面摩擦系数沿x的分布Fig.12 Streamlines and skin friction distributions along x in the windward side

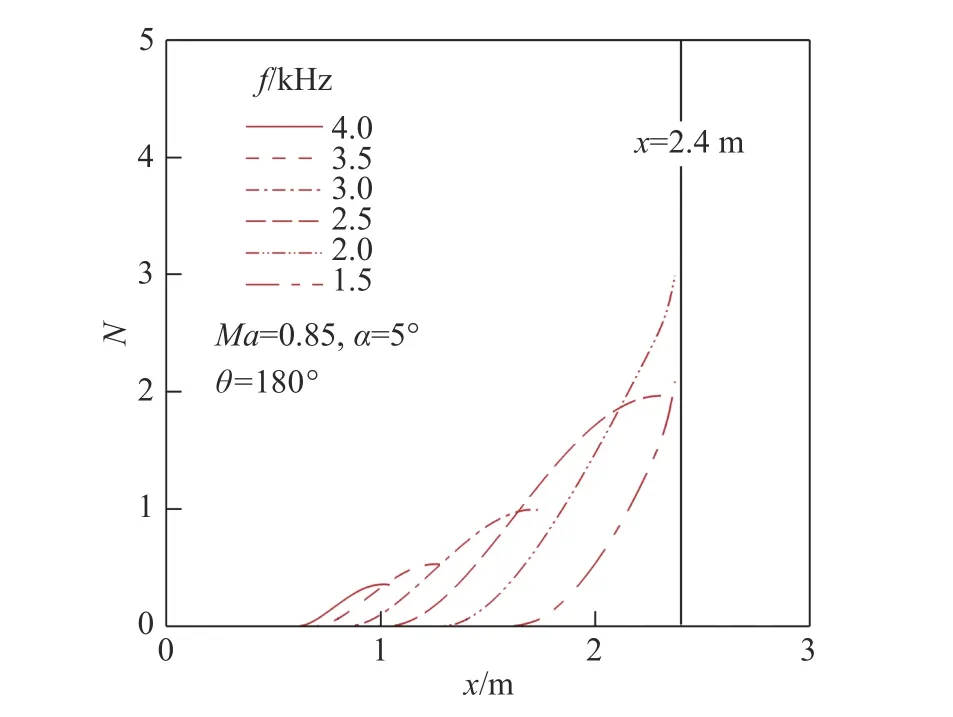
图13 迎风面不同频率T-S波的N值曲线Fig. 13 N factors of T-Swaves with different frequencies in the windward side

对于层流分离泡，通常认为Cf到达最小值的位置可作为转捩位置[40]，即图12（b）所示的x =2.8 m处。在高雷诺数下，流动分离会促使转捩快速发生，对于当前工况，也可近似地把分离发生的位置当作转捩位置。在本文之后的分析中，转捩线存在空档意味着eN方法无法给出转捩位置，实际情况中的转捩由边界层分离引起。

4 关键参数对短舱转捩的影响

4.1 攻角

对于巡航马赫数为0.85的情况，我们还计算了攻角分别为1°、3°的情况，并与前面分析的5°攻角的结果进行比较。

图14（a、b）分别给出了攻角为1°和3°转捩线在短舱上的分布情况。与图11（b）比较可见，随着攻角减小，短舱背风面和迎风面转捩位置的差别减小，除靠近迎风面的区域外，转捩线整体更靠近下游。此外，比较3°攻角和5°攻角的情况，可以发现，3°攻角下，转捩线更加分散。这意味着，转捩判据不确定性引起的转捩位置的误差更大。

图15（a、b）分别给出了Ncri= 5和Ncri= 8时不同攻角下转捩位置随周向角度的变化。可见，当Ncri= 5时，在靠近迎风面的θ = 150°～180°区域内，攻角越小，转捩位置越靠前；而在此之外的背风面和侧面区域，攻角减小使得转捩位置更加靠后。总的来看，攻角的存在使得迎风面附近的区域更加稳定，而背风面及侧面的区域更加不稳定。

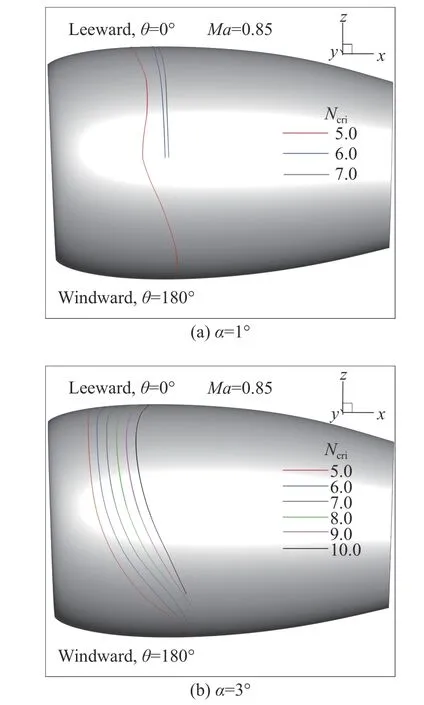
图14 不同攻角的转捩位置Fig.14 Transition locationsunder different anglesof attack

图15 不同攻角转捩位置的比较Fig.15 Comparison of transition locationsunder different anglesof attack

当Ncri= 8时，对比3°攻角和5°攻角的结果可以发现，攻角减小，背风面及侧面大部分区域转捩靠后。当然，还有一种可能是，需要根据实际情况调整转捩判据Ncri的取值。但Ncri取值不同并不影响定性的规律。对于1°攻角的工况，在周向θ =90°～180°范围内，在Ncri≥6条件下eN方法无法给出转捩发生的位置，转捩位置由边界层分离决定。图16（a、b）分别给出了攻角为1°和3°情况下，迎风面θ =180°子午面上的流线分布，可以看到下游均存在流动分离。

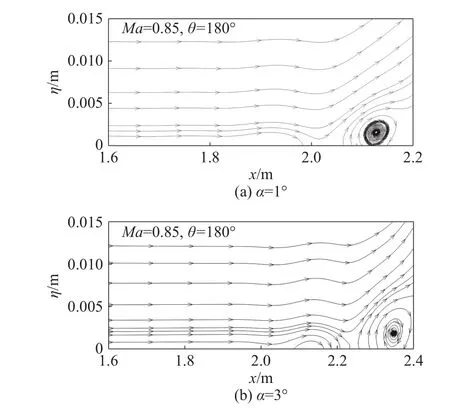
图16 迎风面处的流线分布Fig.16 Streamlinesin the windward side

为了具体说明不同攻角下T-S波的失稳情况，图17（a～c）分别给出了周向θ =45°处不同频率T-S波增长率的等值线图。可以发现，随着攻角减小，失稳区范围和增长率都明显减小。因此，减小攻角抑制了不稳定波的增长，流场变得稳定，转捩推迟发生。前面曾提到，文献[2]通过实验观察到，攻角从0°增加到4°，短舱下部层流区明显增加，与我们的结果是一致的。

4.2 马赫数

在来流攻角为5°时，我们还分析了马赫数分别为0.80和0.89的工况，并与之前分析的马赫数为0.85的工况进行比较，以考察巡航马赫数对转捩的影响。

图18（a、b）分别给出了马赫数为0.80、0.89的转捩预测结果。对比图11（b）可以发现，马赫数减小，转捩线整体更靠上游。并且，对于马赫数为0.8的情况，不同判据下的转捩线分布更为集中。图19（a、b）分别给出了Ncri= 5和Ncri= 8时不同马赫数下转捩位置随周向角度的变化。可见，马赫数增加使得所有子午面上的转捩位置均向下游移动。

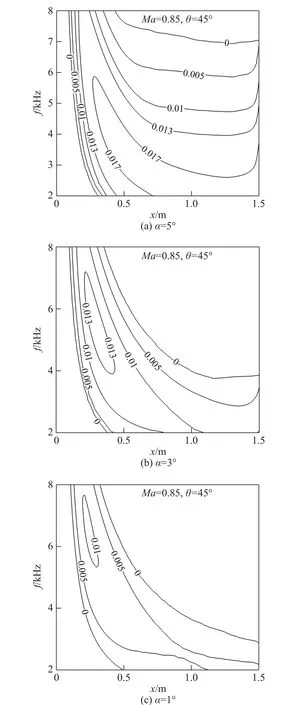
图17 不同攻角的增长率等值线图Fig.17 Growth rate contoursunder different anglesof attack

从图18（b）中可以看出，当马赫数为0.89时，eN方法无法给出迎风面附近区域的转捩位置。此时，转捩位置与边界层分离有关。图20给出了马赫数为0.89工况中θ =180°子午面上的流线分布，可以看出下游存在流动分离。还有一种可能是，转捩仍然是T-S波触发的，而我们选用的转捩判据阈值Ncri太大。这就需要根据实验测试的具体情况调整转捩判据的阈值。但是，不管判据的选择为何，马赫数对转捩位置影响的规律不会改变。

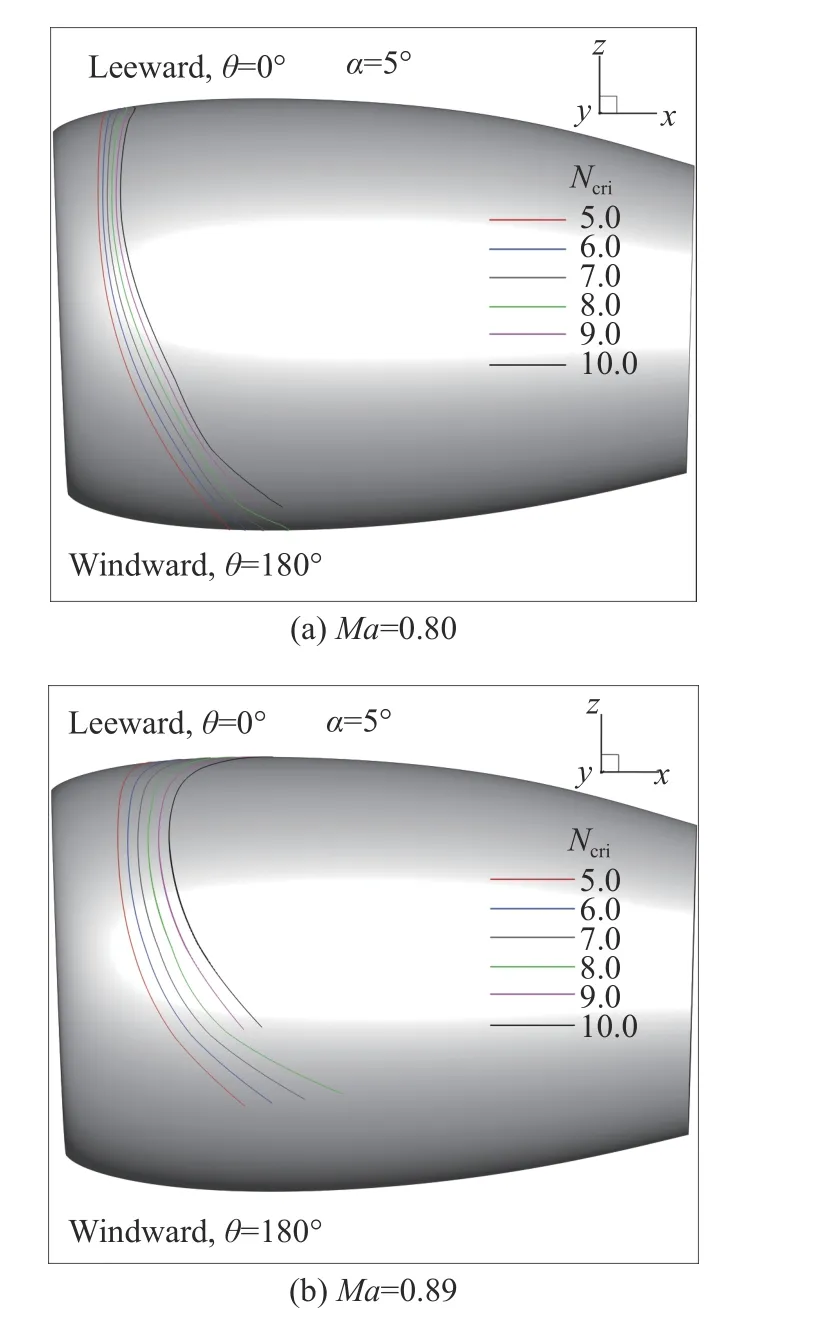
图18 不同马赫数的转捩位置Fig.18 Transition locationsunder different Mach numbers

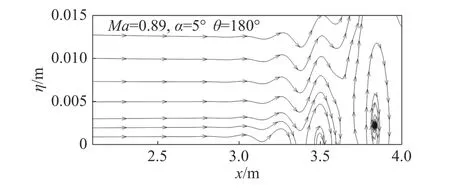
图20 迎风面处的流线Fig.20 Streamlines in the windward side

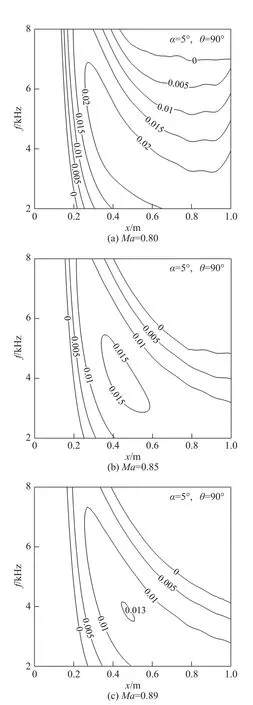
图21 不同马赫数的增长率等值线图Fig.21 Growth rate contours under different Mach numbers

类似地，以周向θ =90°为例，图21（a～c）分别给出了不同马赫数下T-S波增长率的等值线图。可见，随着马赫数的增大，T-S波开始失稳的位置更靠近下游，失稳区逐渐缩小，最大增长率也逐渐降低，流场更稳定，因此导致转捩推迟发生。前面曾提到，杜玺等的实验结果表明[2]，马赫数从0.8增加到0.87，短舱表面层流区明显增加，这与我们的结论是一致的。