基于shapelets时间序列的多源迁移学习滚动轴承故障诊断方法

李 可 燕 晗 顾杰斐 宿 磊 苏文胜 薛志钢

1.江南大学江苏省食品先进制造装备技术重点实验室，无锡，2141222.江南大学机械工程学院，无锡，2141223.江苏省特种设备安全检验监督研究院无锡分院，无锡，214071

0 引言

滚动轴承作为旋转机械的关键零部件，其运行状态的好坏关系着机械系统的稳定性。在机械设备长时间、高负荷的运转过程中，滚动轴承难免会发生故障，轻则影响设备性能，重则引发安全事故,因此，对滚动轴承开展故障诊断研究具有重要的意义[1-2]。

随着计算机运算能力的不断提高，基于深度学习(deep learning，DL)的故障诊断方法近年来得到了研究者的广泛关注[3]。基于深度学习的智能诊断模型具有强大的自适应非线性特征提取和表征能力[4]，无需依赖太多的先验知识和信号处理技术，较基于浅层学习的方法表现出更好的故障诊断能力[5]。INCE等[6]采用一维卷积神经网络实现了电机轴承的实时故障诊断，这种端到端的方式极大提高了故障诊断的效率。ZHANG等[7]将原始的时间信号作为深度神经网络的输入，实现了对滚动轴承故障的分类及相应损坏严重程度的精确判断。SHAO等[8]将一种深度卷积信念网络运用于高铁轴承的故障诊断，诊断准确率达到97%。但是，以上方法的实现需要大量的标记数据，而工程实际中的滚动轴承数据具有以下特点：①价值密度低，机械装备长期处于正常运行状态，轴承故障数据较少；②使用成本高，采集信号蕴含大量噪声，在不可频繁停机检查故障、人工标记数据费时费力的情况下，获取大量带标签数据的过程十分耗时且昂贵。如何在数据有限的条件下获得鲁棒性强的滚动轴承故障诊断模型是一个艰巨的挑战[9]。

迁移学习作为一种运用已有知识求解相似领域问题的方法，可以有效解决样本稀缺的问题，已成为目前故障诊断领域的研究热点。陈超等[10]提出了一种改进最小二乘支持向量机迁移学习方法，运用辅助数据弥补不同工况下滚动轴承可用数据不足的问题，轴承故障诊断精度最大能提高30%。HAN等[11]提出了一种深度对抗迁移网络诊断模型，引入对抗学习作为跨域正则化项，分别将不同载荷工况下的数据作为源域与目标域，通过迁移学习实现了小样本条件下滚动轴承故障的精确诊断。PANG等[12]利用跨域堆叠降噪自编码器实现了跨领域滚动轴承故障诊断。上述基于迁移学习的故障诊断方法证明了通过知识迁移提高滚动轴承故障诊断精度的可行性，但它们都是采用相同设备在不同工况下的试验数据来验证迁移效果的。如果源域与目标域的相关性不强，那么迁移学习有可能出现负迁移与次优解的问题。相比单源迁移学习，多源迁移学习不仅可以从多个源域中挖掘出更多的知识用于目标域的学习，还能通过发现与目标域更相似的源域来避免负迁移问题。ZHENG等[13]提出了一种基于多源域泛化的智能故障识别方法，有效降低了负迁移的风险；徐丹雅[14]提出了一种基于多源域自适应机械故障诊断方法，将多种工况下采集的数据融合为源域数据集，实现了新工况下的故障诊断。然而，以上方法局限于同一机械设备轴承的多工况故障诊断。SHI等[15]提出了一种基于多源域自适应的无监督迁移学习方法，从多个来源学习通用诊断知识并用于完成目标任务；FENG等[16]构建了一个GlobalNet来融合多源信息，实现了跨域故障诊断。但他们提出的方法适用于目标域样本数据充足的情况。针对小样本问题，SUN等[17]利用基于元学习的多源迁移学习实现了图片的准确识别，但如何基于多源迁移学习实现滚动轴承跨域故障诊断仍有待研究。

Shapelets是时间序列中最具辨别性的子序列[18]，通过提取轴承数据的shapelets来度量源域与目标域的相关性，可有效降低出现负迁移的可能性。本文提出一种基于shapelets的多源迁移学习滚动轴承故障诊断方法，该方法充分利用已有不同设备的轴承数据，通过多源迁移学习以训练无法获取充足数据、有强噪声干扰的其他设备的轴承故障诊断模型，有效提高了小样本与强噪声情况下滚动轴承故障诊断精度。该方法首先利用基于动态时间规整(dynamic time warping，DTW)的shapelets学习算法提取源域与目标域的判别结构，然后度量判别结构之间的相关性，优化源域网络并进行参数迁移，再自适应地设置域权重，实现对分类结果的聚合。最后通过滚动轴承实验验证本文方法的有效性。

1 基于DTW的shapelets提取

1.1 DTW距离

DTW是一种能够有效度量两个不等长时间序列之间相似性的算法，它基于动态规划的思想寻找两个时间序列间的最优弯曲路径，可实现不等长时间序列距离的计算。如图1所示，t和t′分别代表两个时间序列，i和j代表时间序列中第i与第j个点。累积距离Dti,t′j为当前格点欧氏距离d(ti,t′j)与可以到达该点的最小的邻近元素的累积距离之和：

Dti,t′j=d(ti,t′j)+min(Dti-1,t′j-1,Dti-1,t′j,Dti,t′j-1)

(1)

两个时间序列之间DTW距离的计算公式如下：

D(t,t′)=Dtq,t′q′

(2)

式中，q、q′分别为时间序列t和t′的长度。

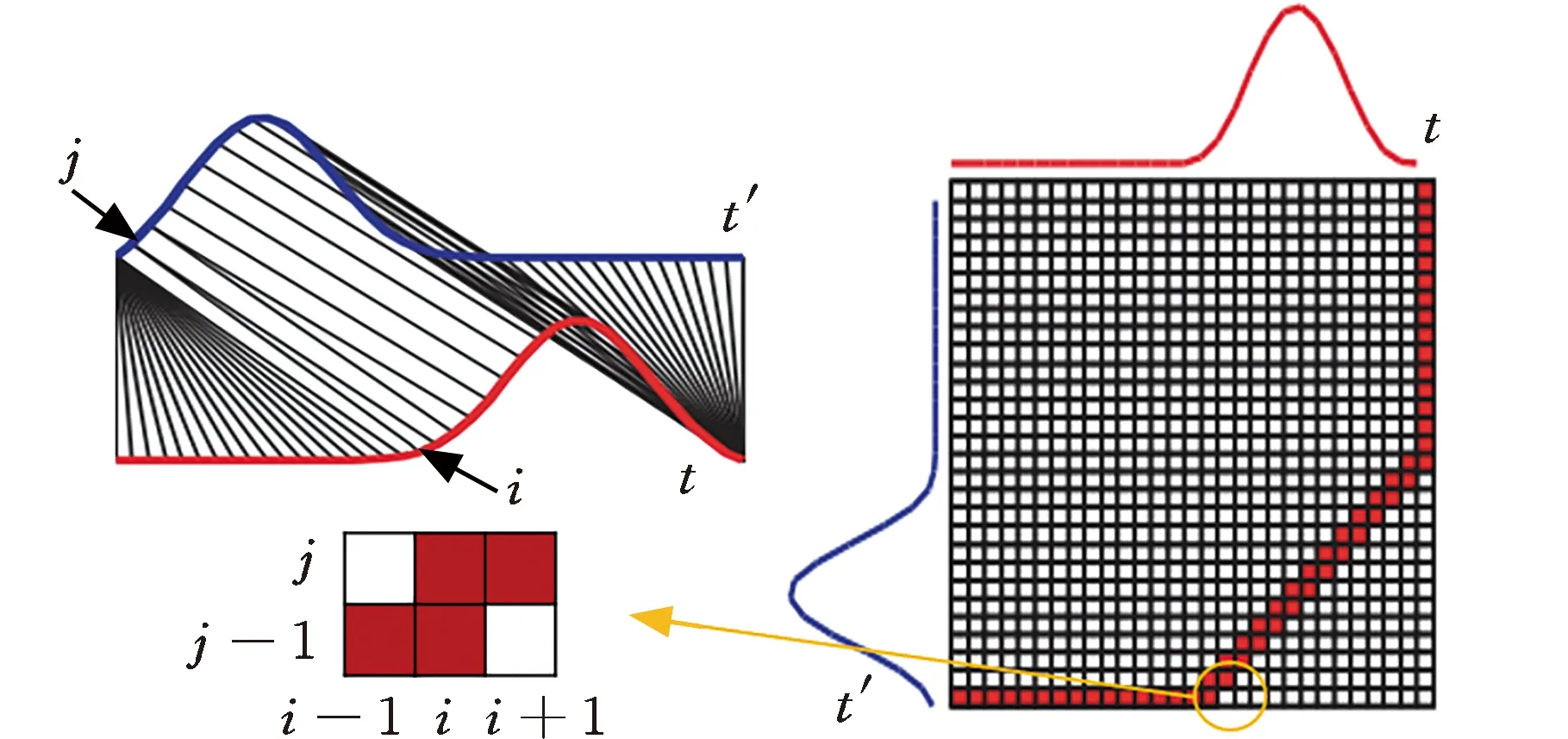
图1 DTW示意图

1.2 基于DTW的shapelets学习算法

滚动轴承振动信号具有信息冗余、噪声大、非线性等特点，度量轴承数据相关性的难度较大。本文提取轴承振动信号的shapelets作为判别结构以度量源域与目标域的相关性，从而降低计算的空间与时间复杂度，提高相关性算法的可靠性与准确度。

以T表示一个时间序列，具有M个样本的时间序列数据集可表示为T={T1,T2,…,TM}。以S表示一个shapelet，K表示要学习的shapelets的总数，则数据集的shapelets可表示为S={S1,S2,…,SK}。Shapelets学习算法[19](learning time-series shapelets，LTS)是一种基于随机梯度学习算法求解最佳shapelets的方法，该算法首先通过在第i个时间序列Ti上滑动一个长为L的窗口，以提取Ti中所有可能的片段；然后以Ti，p:p+L-1代表Ti上第p个长度为L的片段，第k条shapelet与子序列Ti，p:p+L-1之间的距离可以表示为

Di,k,p=D(Ti,p:p+L-1,Sk)

(3)

Ti和Sk之间的距离Mi,k定义为Ti的每个片段与Sk的DTW距离中的最小值：

(4)

式中，P为Ti中片段总数。

以这些最小距离作为特征，用随机梯度下降法学习逻辑回归分类模型以求取时间序列数据集的shapelets，其学习对象为

(5)

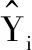
损失函数为

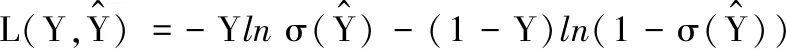
(6)

式中，σ为sigmoid激活函数；Y为类别标签。

目标函数为

(7)

式中，N为数据集的类别数；Ω为L2正则化项；λ为正则化系数；W为超平面参数。

可通过随机梯度下降算法更新S和W[19]。

LTS算法中需要计算模型损失函数的导数，然而式(4)是不可导的,因此，本文采用软最小化函数近似代替：

(8)

其中，参数α用来控制软最小化函数和最小化函数的接近程度，当α→-∞时软最小化函数近似等于最小化函数。

2 多源迁移学习网络

本文提出的多源迁移学习算法根据多个源域与目标域之间的相关性，有选择地将在源域上学习到的知识迁移到目标域上，从而避免学习到的模型被样本上潜在的对抗性分布误导。

2.1 源域网络预训练

选取一维全卷积网络[20](fully convolutional networks，FCN)作为多源迁移学习的网络结构，网络的输入为一个可变长度的时间序列，输出为数据集N个可能类的概率分布。为了从源域中提取更多能有效区分故障的特征，每个源域Qi都需要预训练特征提取器Fi和分类器Ci。Fi和Ci通过以下的交叉熵损失函数优化：

L(Fi,Ci)=

(9)

式中，E为数学期望；pi为数据Ti的分布；R为指示函数。

值得注意的是，在源域网络预训练阶段，不同源域之间的权重是不共享的。与共享特征提取器的网络相比，非共享特征提取网络可以有效避免领域偏移与类别偏移问题，将诊断结果进行聚合时可以更好地提高目标域的诊断能力。

在源域数据集上完成上述网络的训练之后，得到了等同源域数量U的全卷积网络。它们在结构上的唯一区别是最后一层的softmax分类器Ci，其结构取决于对应数据集中的类别数。

2.2 源域网络优化

将提取的各数据集的shapelets作为判别结构，降低了度量源域与目标域之间相关性的难度。在此基础上，可以进一步优化源域数据，剔除与目标域相关性不大的样本，并基于新的源域数据对预训练模型进行微调。

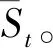
2.3 诊断结果聚合

诊断模型的最终目的是能够实现对目标信号Tt的准确分类。首先，对于训练后的源域网络，移除Ci并添加一个运用Glorot方法[22]初始化的C′i。然后运用目标域数据对整个源域网络微调更新，以获得更好的效果[23]。最后聚合各个源域分类器的结果获得最终的诊断结果：

(10)

(11)

3 实验验证

风机滚动轴承是风机中极易产生故障的零部件,在工程实际中，采集的风机轴承监测数据具有典型故障信息不足、标签匮乏、环境噪声大的特点，难以用于训练高精度智能诊断模型。本文搭建风机轴承故障诊断实验平台，模拟实际运行过程中轴承故障情况。实验设备如图2所示，加速度传感器型号为PCBMA352A60，输出带宽为5～60 000 Hz，灵敏度为10 mV/g。转速恒定为1000 r/min，采样频率为10 kHz，采样时间为2 s。如图2所示，通过线切割技术分别在轴承内圈、外圈、滚动体加工出0.3 mm×0.05 mm(宽×深)的微小伤痕以模拟轴承故障。

3.1 迁移诊断数据集

(a)实验平台

(b)故障轴承图2 实验平台及故障轴承

选用的滚动轴承数据集见表1。 数据集GA来自于德国帕德伯恩大学轴承数据中心。数据采自6203型滚动轴承，包括正常及损伤直径为0.25 mm的内圈故障和外圈故障共三种状态，采样频率设置为25 kHz，转速为12 000 r/min。数据集GB来自美国凯斯西储大学的轴承数据中心,数据采自SKF6205型滚动轴承，三种故障损伤均有0.1778、0.3556、0.5334 mm三种尺寸，共10类样本。采样频率设置为12 kHz，电机转速为1797 r/min。数据集GC源自多级齿轮传动试验台，该试验台主要由电动机、定轴齿轮箱、行星齿轮箱等组成。数据采自定轴齿轮箱的LDK UER204型滚动轴承。每种状态的样本在电动机转速为1200 r/min、空载下采集，故障损伤直径均为0.3 mm，采样频率为12 kHz。数据集GD源自实验室转子试验台，该试验台主要由电动机、飞轮、带传动负载等组成，数据采自ER-12K型滚动轴承。电动机转速为1450 r/min，采样频率为12 kHz。数据集GE源自本文的风机轴承故障诊断试验平台，共有1600个样本，每种状态的样本数为400。

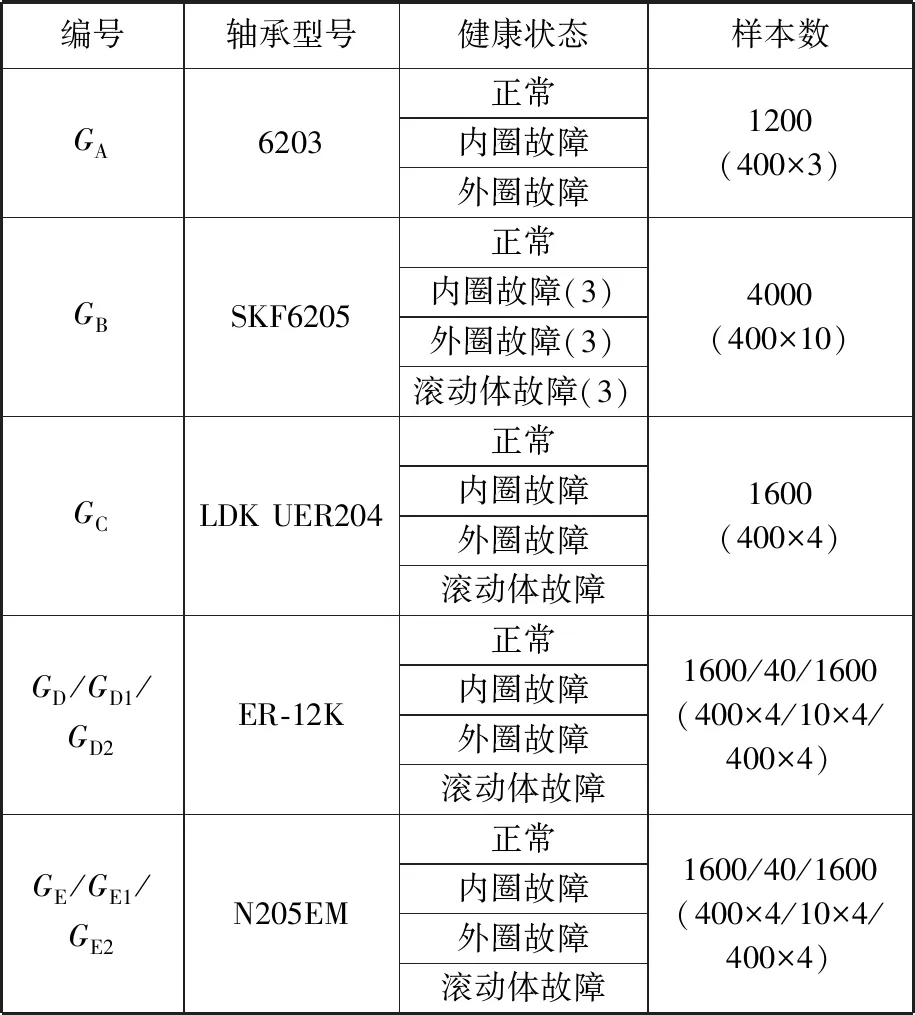
表1 滚动轴承数据集

从数据集GD中每类取10个样本，共计40个样本，构成小样本数据集GD1，用于验证本文方法在小样本情况下的诊断效果。同时，对数据集GD添加-20 dB的高斯白噪声构成强噪声数据集GD2，用于验证本文方法在强噪声情况下的诊断效果。针对数据集GE以同样的方式制作GE1、GE2数据集。

3.2 故障诊断结果

在诊断模型的训练过程中，本文方法的主要参数设置如下：shapelets的长度L设置为50，shapelets数量K设置为10，软最小化函数中的α设置为-100。

源域训练过程中FCN参数设置如下：Batch size为16，迭代次数为2000，选用Adam优化器自适应调整步长，学习率为0.001。目标域训练过程中迭代次数为50。

3.2.1多源与单源迁移效果对比分析

单源迁移效果如图3所示，图中四种颜色分别代表四种数据集，灰色为无迁移FCN网络迭代2000次训练诊断结果，将计算10次的试验平均值作为最终准确率。由图3与表2可以看出，在单源域迁移情况下，小样本数据集GD1和GE1的诊断准确率有所提高，但选择的源域不同，准确率的提高效果有极大差别。当源域为GC时，GD1的诊断准确率取得了较大的提高；当源域为GB时，GE1的诊断准确率取得了极大的提高。从数据集GD2和GE2的结果可以看出，采用不同的数据集作为源域进行迁移时，强噪声轴承数据的诊断结果存在较大差异。当源域为GA时，GE2出现了负迁移现象。当源域为GC时，GE2的迁移诊断效果达到了94.28%，为所有单源域迁移实验中效果最好的，但GE1的迁移诊断效果并不突出，仅有55.85%，离目标域为GE1的所有实验中准确率最高的86.70%有较大差距。同样的现象也出现在GA对GD1和GD2的迁移结果上。当源域为GE2的时候，GD1的诊断准确度有很大的提高，GD2的提高效果却不突出。说明源域网络迁移的知识是有区别的，有些针对强噪声目标域有优势，有些针对小样本目标域有优势。

图3 不同数据集单源迁移效果

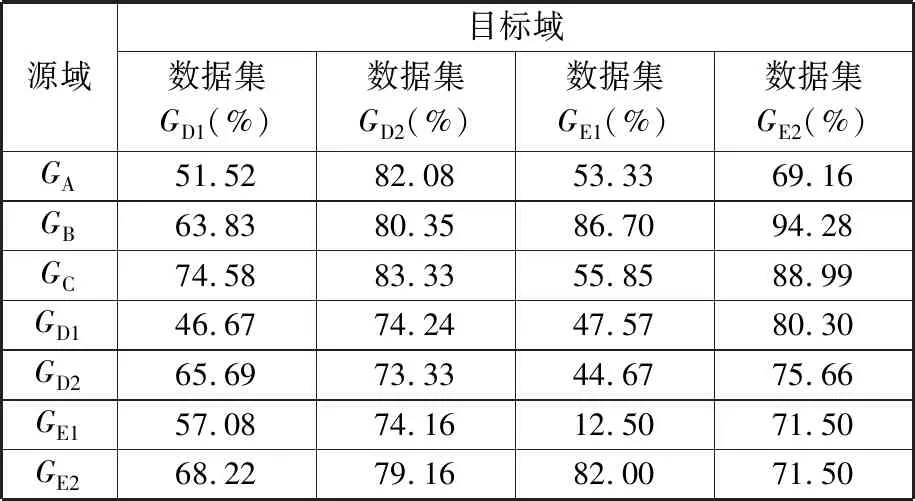
表2 单源域迁移平均准确率

由于单源迁移对故障诊断提升效果不稳定，因此通过多源迁移聚合诊断结果是有价值的。将本文所提出的方法与FCN、支持向量机[10](support vector machine，SVM)、迁移成分分析[24](transfer component analysis，TCA)、模型无关元学习[25](model-agnostic meta-learning，MAML)进行对比试验，FCN为本文迁移学习方法的基础网络，由输入层、128×8×1、256×5×1、128×3×1的三层卷积层，全局平均池化层与softmax分类层组成；SVM的核函数为高斯核函数，核函数参数σ=4，惩罚系数C=2；TCA中选择线性核函数映射，其权衡参数μ=1、γ=0.5，源域为GC；MAML模型中元学习率为0.005，任务学习率为0.05。MAML与本文方法实验中源域为GA、GB、GC，目标域分别为GD1、GD2、GE1、GE2。

如图4与表3所示，本文方法在小样本数据集GD1和GE1的故障诊断中，准确率相较于FCN、SVM、TCA与MAML有极大提高，体现了多源迁移诊断的优越性，证明了利用典型故障信息充足的实验室样本可以实现精确的小样本轴承故障诊断。在强噪声数据集GE2的诊断结果中，多源迁移通过域权重的自适应选择可以有效避免强噪声情况下的负迁移现象，如表3所示，诊断准确率可达97.29%，GD2效果虽不如GE2，但依然取得了95.76%的准确率。

图4 不同模型诊断准确率

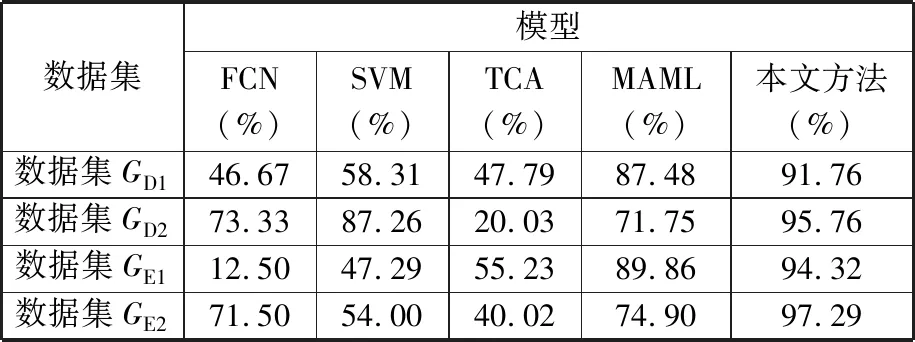
表3 不同模型故障诊断平均准确率

3.2.2shapelets效果验证

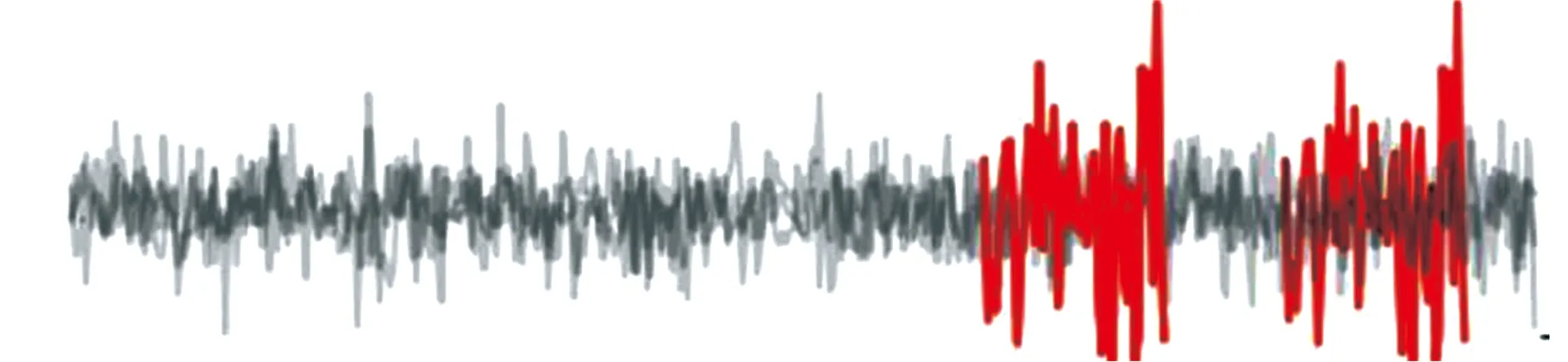
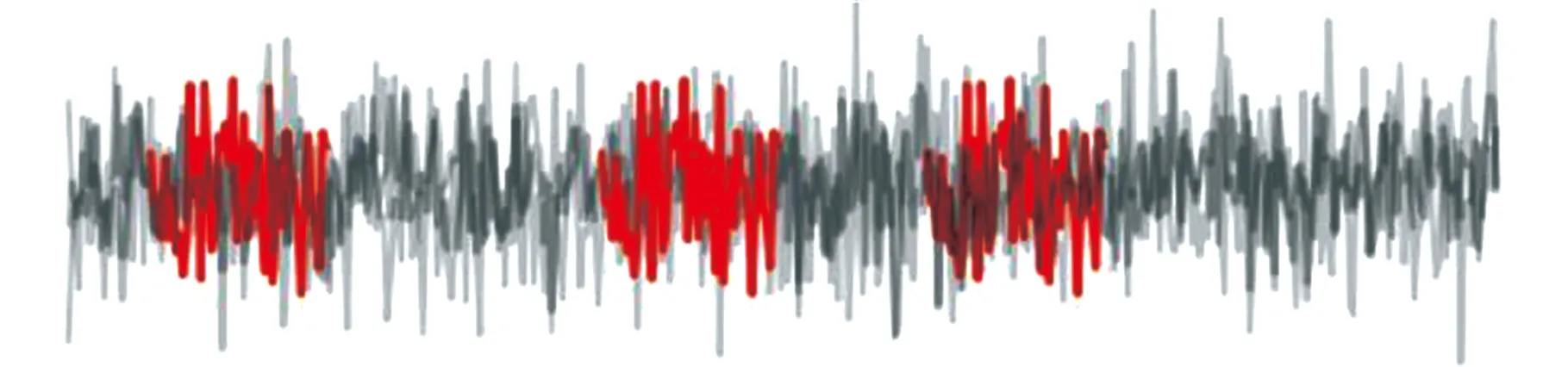
为了验证shapelets在判别源域与目标域相似性上的优势，对数据集shapelets进行可视化处理，结果如图5所示。图中灰色线条是7组数据集的内圈故障信号，红色部分为提取的shapelets。

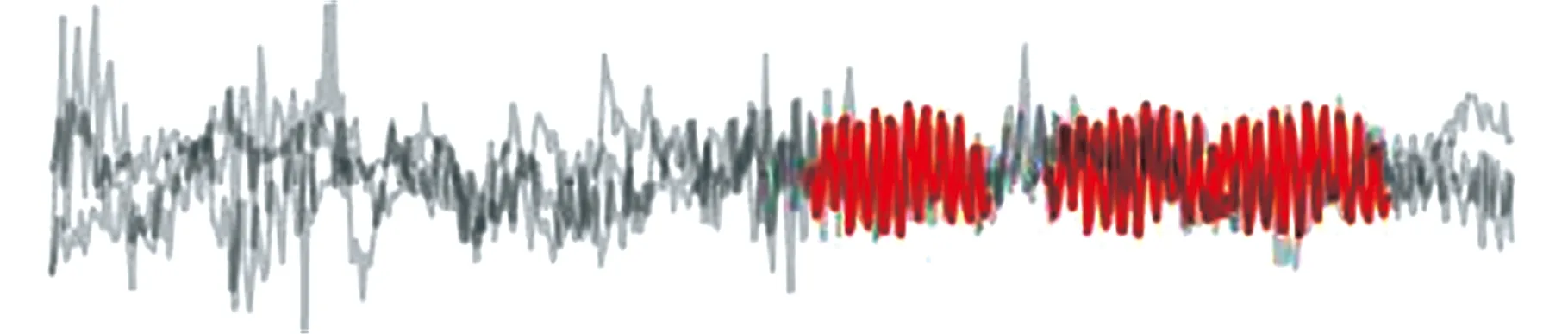
(a)数据集GA的shapelets

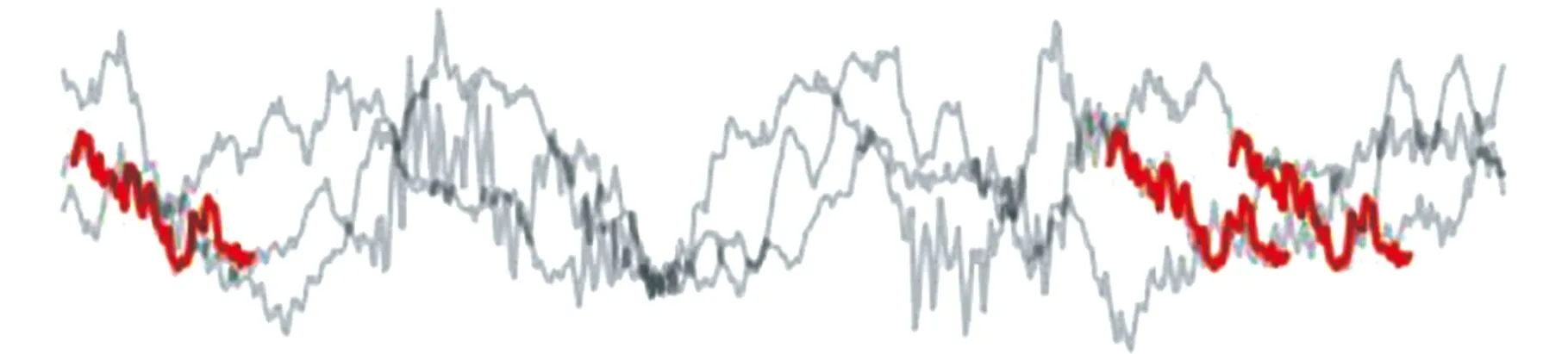
(b)数据集GB的shapelets

(c)数据集GC的shapelets

(d)数据集GD1的shapelets

(e)数据集GD2的shapelets

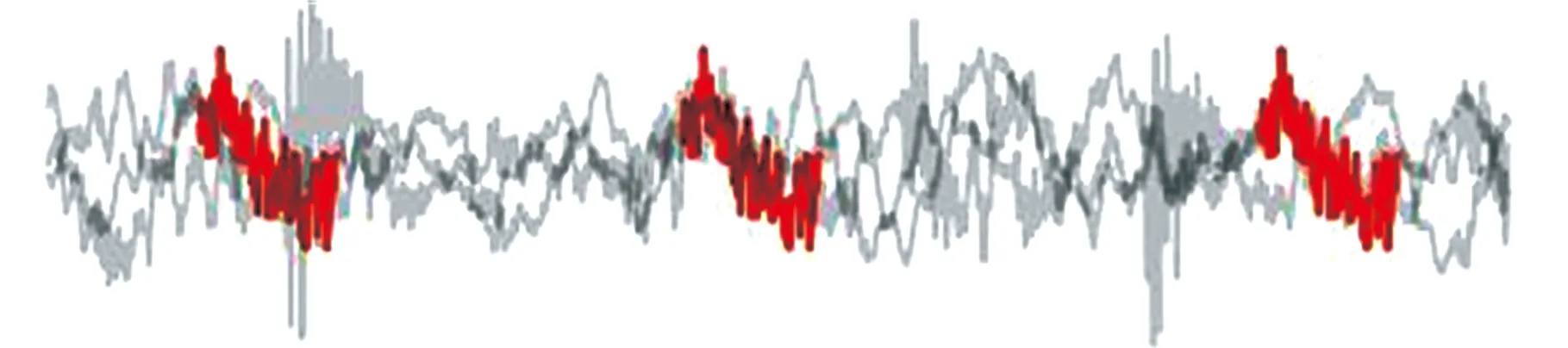
(f)数据集GE1的shapelets

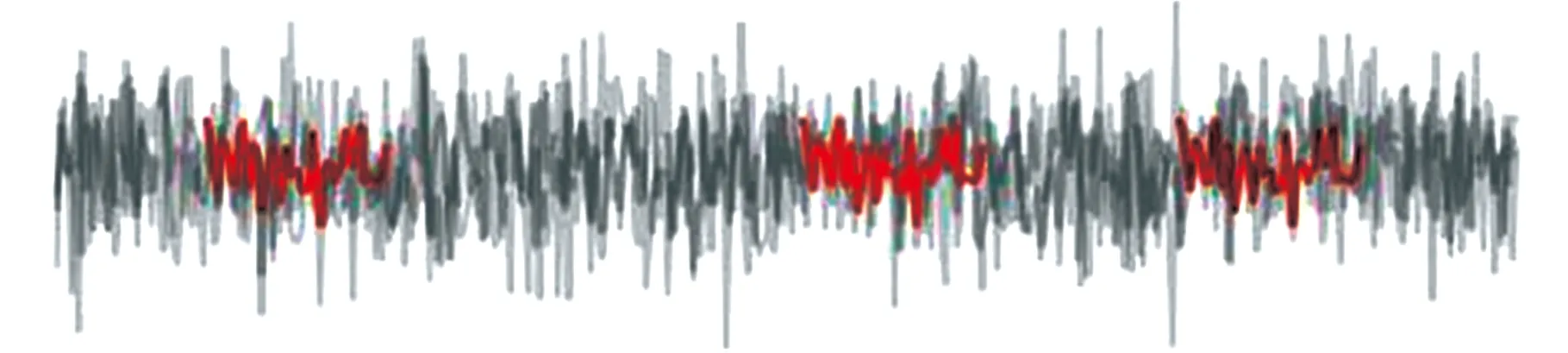
(g)数据集GE2的shapelets图5 shapelets样例

各数据集shapelets之间距离如表4所示。可以看出，单源域情况下对GE1迁移效果最好的数据集是GB，其shapelets与GE1也最接近，DTW距离为74.1，而提升效果最差的数据集GA距离为637.5。数据集GD2和GE2在有噪声干扰下，依然可以提取出有效应用于目标域与源域判别的shapelets，其中GE2与GE1的距离为137.1，是GE2的shapelets与其他数据集shapelets中最短的，而GD2与GD1的距离也接近最短值。

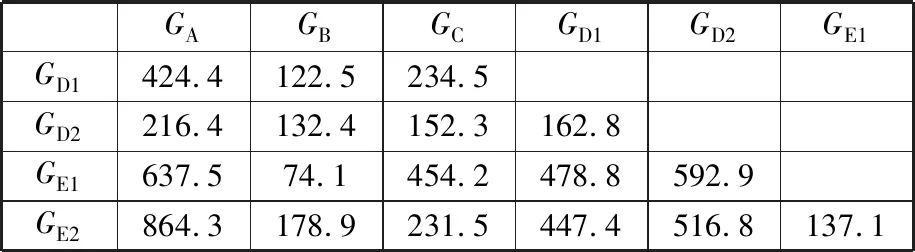
表4 各数据集shapelets之间距离

4 结论

(1)提出了一种基于shapelets的多源迁移学习方法，并将其应用于滚动轴承的故障诊断。该方法充分利用已有轴承数据，帮助训练无法获取充足数据、有强噪声干扰的其他设备的轴承故障诊断模型。

(2)所提出的基于shapelets的判别结构可以筛选源域中与目标域的近似样本，并利用这些样本对源域网络进行微调，有效提高源域网络的可迁移性能。通过设计权重机制实现了多源特征聚合分类，进一步降低了源域与目标域差异性的影响，相较于现有的多源故障诊断方法，有效解决了基于深度学习的故障诊断方法在样本不足情况下精度低的问题。

(3)将提出的方法分别用于转子试验台与模拟风机试验台轴承故障诊断，并与其他方法(全卷积网络、支持同量机、迁移成分分析、模型无关元学习)进行对比，结果表明，所提方法在小样本与高噪声情况下具有更好的滚动轴承故障诊断性能。