含弹簧阻尼装置空间机器人捕获卫星分数阶超扭滑模缓冲柔顺控制

朱 安,陈 力

(福州大学机械工程及自动化学院,福州 350116)

1 引言

太空中大量的失效卫星使空间轨道资源被极大浪费,因此使用空间机器人对失效卫星进行回收受到广泛关注[1-3]。与单臂空间机器人相比,双臂空间机器人具有大载荷、高灵活性等优点,是捕获操作研究的重点[4-6]。空间机器人捕获卫星的过程大致可分为观测、靠近、抓捕与镇定控制4个阶段。由于非合作卫星具有高速、旋转特性,在抓捕阶段其将与机器人末端执行器发生猛烈碰撞,由此产生的巨大冲击力易造成机器人关节损坏,冲击效应也会使镇定控制更具挑战,因此第3、第4 阶段直接关系到捕获操作的成功与否。

针对第3 阶段,Lin 等[7]针对冗余空间机器人捕获目标的碰撞问题,提出了一种由简化阻抗控制器和增广结构控制器组成的控制方案;Moosavian 等[8]为协调捕获操作中基座、臂杆及目标航天器等各个系统,提出了一种多阻抗控制律;陈钢等[9]利用碰撞过程中的冲量原理建立了碰撞动力学模型。然而在捕获非合作卫星时,若未在脆弱的关节处添加保护措施,关节容易被冲击载荷破坏。地面机械臂通常将串联弹性执行器(Series Elastic Actuator,SEA)添加到关节处,以防止末端执行器与外界环境碰撞造成关节破坏。

针对第4 阶段,Zhang 等[10]针对抓取大惯性非合作目标,提出了一种动量降低和动量再分配的协调控制方案;Wu 等[11]针对捕获快速翻滚目标,设计了一种分解运动导纳控制方法;Huang等[12]针对捕获卫星后反作用轮结构发生变化,提出了一种改进的SDRE(Sate-Dependent Riccati Equation)最优控制器。滑模控制结构简单、鲁棒性强,被广泛应用于各类系统的控制。但滑模控制也存在稳态误差大、响应速度慢、奇异和抖振等缺点。为了解决这些问题,终端滑模控制采用非线性曲面,保证了鲁棒性和快速收敛性[13-14],但抖振问题依然存在。超扭终端滑模可在保证高控制性能的同时,有效地消除抖振问题,近年来受到了广泛关注[15-16]。此外,基于分数阶的终端滑模控制,特别是速度、加速度等无法测量的系统中,可有效地提高系统快速收敛和轨迹跟踪性能,且稳态误差较小[17-18]。

综上所述,为在空间机器人捕获非合作卫星的过程中保护关节不受冲击破坏,本文在关节电机与机械臂之间添加一种弹簧阻尼装置(Spring Damper Device,SDD),相较于SEA,SDD既能利用弹簧实现冲击载荷的快速缓冲、卸载,又可通过阻尼器抑制柔性振动。另外,针对关节受空间限制未能安装速度、加速度传感器导致无法测量速度、加速度的问题,通过三阶观测器对速度、加速度进行重构;针对捕获后混合体系统的镇定控制,提出一种匹配SDD 的分数阶超扭滑模柔顺控制策略,并利用数值仿真对该策略进行验证。

2 SDD 模型结构与柔顺策略

2.1 SDD 模型结构

SDD 的结构如图1 所示,主要包含旋转阻尼器与扭转弹簧,且阻尼器嵌套在弹簧内部与弹簧同步运动。扭转弹簧用于传动与冲击能量的吸收,旋转阻尼器则提供阻尼力抑制柔性振动。图1 中Ksk、Dtk(k =1,2,···,6)分别为SDD 中弹簧刚度与阻尼系数,Dmk、DLk分别为电机、机械臂端的等效阻尼系数。

图1 SDD 结构Fig.1 Structure of the SDD

2.2 柔顺策略描述

由于SDD 是被动装置,捕获非合作卫星时,冲击效应将使混合体系统处于翻滚的状态,此时若未对电机添加约束,产生的瞬时冲击力矩很容易对关节造成损坏。为此,本文同时设置了电机的关闭与开启阈值,其中关闭阈值用于限制瞬时冲击力矩,开启阈值可防止电机频繁开关机。当检测到冲击力矩超过所设关机阈值后电机关闭,当SDD 将冲击力矩降低到开启阈值后电机将再次开启。

3 动力学模型

双臂空间机器人捕获卫星如图2 所示。图2中,O0、Os、Oi分别为载体质心、卫星质心、各关节铰中心,XOY为惯性参考坐标系,x0O0y0、xsOsys、xiOiyi分别为固定在载体质心、卫星质心、关节铰中心上的坐标系。

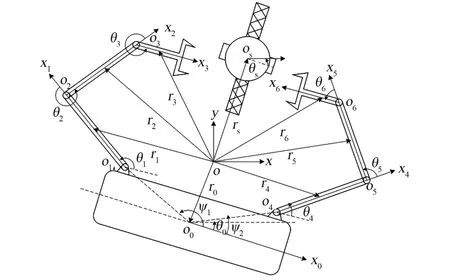
图2 配置SDD 的双臂空间机器人与被捕获卫星系统Fig.2 Dual-arm space robot with SDD and captured satellite system

参考文献[19],可得配置SDD 的双臂空间机器人捕获卫星后的闭链混合体系统动力学模型为式(1):

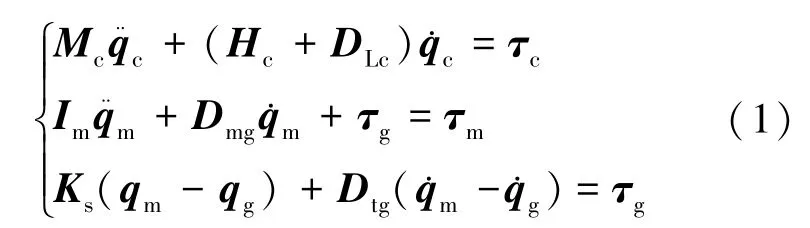
式中:Mc∈R4×4为惯量矩阵,∈R4×1分别为包含科氏力、离心力列向量,Im∈R6×6为电机转子转动惯量矩阵,DLc∈R4×4为左臂等效阻尼系数矩阵,Dmg∈R6×6为电机等效阻尼系数矩阵,Dtg∈R6×6为阻尼器的阻尼系数矩阵,Ks∈R6×6为弹簧刚度矩阵。qc= [θ0,θ1,θ2,θ3]T,qg=[θ1,θ2,···,θ6]T,qm=[θm1,θm2,···,θm6]T,τc= [τ0,τ1,τ2,τ3]T,τg= [τ1,τ2,···,τ6]T,τm= [τm1,τm2,···,τm6]T。

捕获目标卫星后混合体系统速度为式(2):

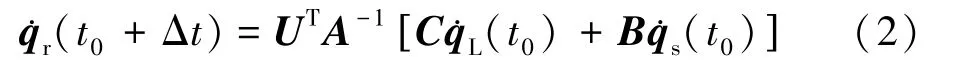
式中:qL= [x0,y0,qTc]T,qs= [xs,ys,θs]T,B∈R6×3,A、C∈R6×6为包含系统参数的矩阵。

碰撞冲击力为式(3):

式中:fp= (Jr)+Mr[(t0+Δt)-(t0)] ,Jr∈R6×9为机械臂抓手捕获点的运动雅克比矩阵,Δt为碰撞时长。

4 控制器设计

本文设计的分数阶超扭滑模柔顺策略既保持了传统滑模结构简单、对外界噪声干扰和参数摄动鲁棒性强的特点,同时也克服了稳态误差大、响应速度慢、奇异和抖振等缺点,可较好地实现对碰撞后失稳的混合体系统快速、高精度的镇定控制。

4.1 数阶微分与积分

函数f(t)的Riemann-Liouville(RL)分数阶微分与积分定义如式(4)、(5)所示[20]。

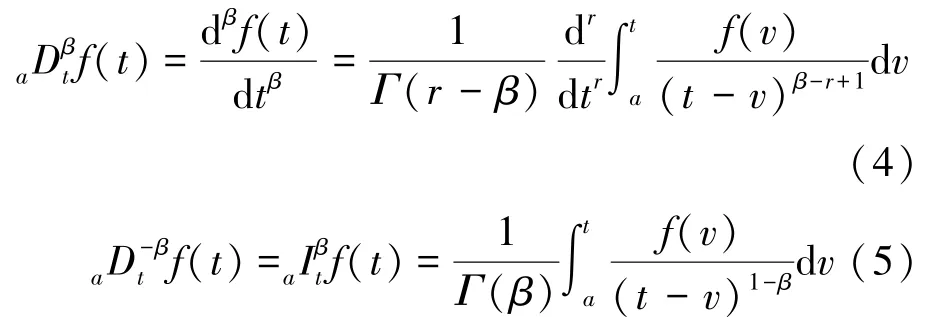
式中:r-1＜β ＜r,Dβ、Iβ分别表示分数阶微分与积分,Γ(·)为Euler-Gamma 函数,其表达式如式(6)所示。

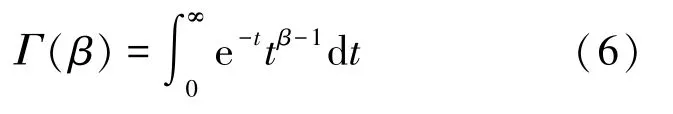
函数f(t)的分数阶微分的n阶导数为式(7)[20]:

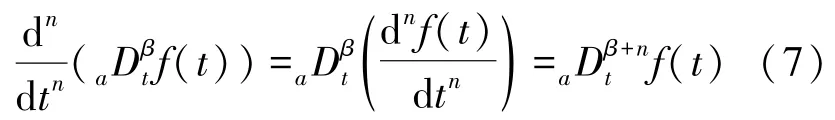
4.2 三阶观测器设计

通常出于体积、质量、蓄电池电压和成本等原因,空间机器人一般只装有位置反馈器,而未装有速度、加速度测量装置。因此,本文利用位置反馈对速度、加速度进行重构。

将混合体系统模型改写为式(8):

将速度、加速度重构为式(9)[21]:

假设1:观测误差与系统不确定项的和有界,如式(10)所示。

4.3 分数阶超扭滑模策略

设计如式(11)所示形式的分数阶超扭滑模面:

对式(11)求导可得式(12):

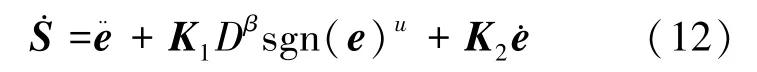
结合式(8)、(12)可得式(13):

基于式(1)、式(11),设计如式(14)所示形式的分数阶超扭滑模控制器:

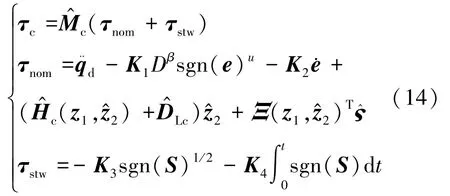
将式(14)带入式(13),且结合假设1 可得式(15):

为实现系统稳定,将ς的自适应率设计为式(16):

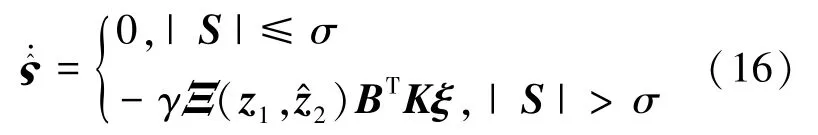
式中:σ＞0 为避免参数漂移的死区大小,γ＞0为增益系数,B= [1/ |S|1/2,01×7]T,ξ=[sgn(S)1/2,χ]T

设计如式(17)所示的Lyapunov 函数:

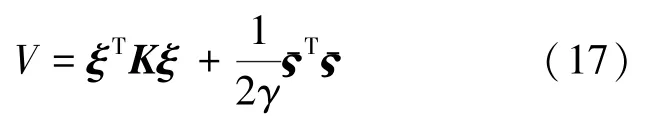
对ξ求导且代入式(15)可得式(18):

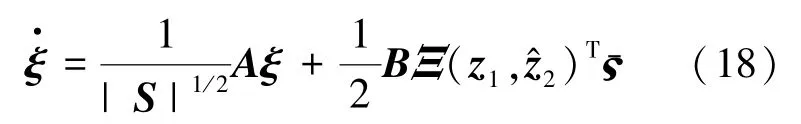
通过式(18)可得V的导数为式(19):

将式(16)带入式(19)可得式(20):

通过式(20)可知系统稳定。

5 数值仿真分析

5.1 第3 阶段SDD 抗冲击性能模拟

双臂空间机器人系统参数:m0= 200 kg,mi=10 kg(i =1,2,4,5),mj= 5 kg(j =3,6),Li= 2 m,Lj= 1 m,di= 1 m,dj= 0.5 m,I0= 128 kg·m2,Ii=15 kg·m2,Ij= 2 kg·m2,Imk= 0.05 kg·m2(k=1,2,…,6),ksk= 1000 N/rad,Dmk= 28.65 N·s/rad,Dtk= 1146 N·s/rad,DLk= 28.65 N·s/rad,ψ1=2.791 rad,ψ2= 0.349 rad。卫星参数:ms= 75 kg,ds= 0.5 m,Is= 9.5 kg·m2。空间机器人的初始位置为q= [10°,120°,- 60°,- 60°,60°,60°,60°]T。

为了验证SDD 在第3 阶段的抗冲击性能,在多组卫星速度下对关节受到的冲击力矩进行力学模拟,结果如表1 所示。卫星速度为= [xs,ys,θs]T,为沿x轴方向的线速度,为沿y轴方向的线速度,为绕z轴旋转的角速度。

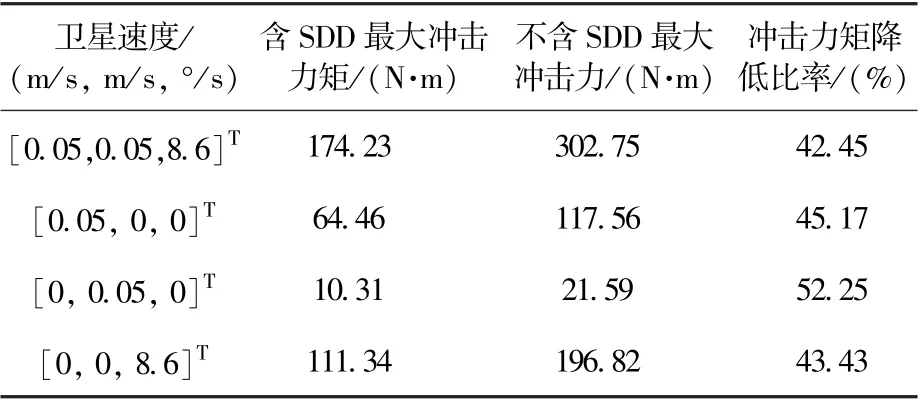
表1 不同卫星速度下SDD 抗冲击性能对比Table 1 Comparison of impact resistance of SDD at different satellite velocities

由表1 可得,在第3 阶段机器人捕获不同速度的卫星,SDD 均能起到较好的缓冲作用,且最大可将碰撞冲击力矩降低到52. 25%,因此认为SDD 在碰撞过程能很好保护关节。

5.2 第4 阶段柔顺策略性能模拟

系统控制参数:αn =2(n =1,2,3),β =0. 6,u =0. 8,σ =0. 01,γ =0. 1,K1=diag(50,50,50,50),K2= diag(40,40,40,40),K3= diag(10,10,10,10),K4= diag(10,10,10,10)。空间机器人的初始位置、速度与4. 1 相同,卫星速度q·s(0)= [0. 05,0. 05,8. 6]T,镇定控制过程中混合体系统的期望状态qd= [10,120,- 60,- 60,60,60,60]T。假设电机在发生碰撞1. 5 s 后开机。通过式(1)、(2)可计算出电机开机时混合体系统的位置q= [10. 44,120. 48,- 63. 57,- 52. 21,62. 82,52. 73,68. 94]T,仿真时间为15 s。

假设电机负载时关节能承受的冲击力矩为170 N·m ,为了充分地保护关节,设置关机力矩阈值FC= 150 N·m ,开机力矩阈值FO=20 N·m。

仿真结果如图3～图7 所示。图3 为镇定控制过程中电机的开关机信号(1 表示开机,0 表示关机),图4 为关节所受瞬时冲击力矩变化,图5为载体姿态角跟踪轨迹,图6 为左臂3 个关节角跟踪轨迹,图7 为右臂3 个关节角跟踪轨迹。

图3 电机开关机信号Fig.3 Switch signal of joint motor

图4 关节所受冲击力矩Fig.4 Impact torque on joints

图5 载体姿态角轨迹Fig.5 Trajectory of the base attitude

图6 左臂关节角轨迹Fig.6 Trajectory of left arm joint angles

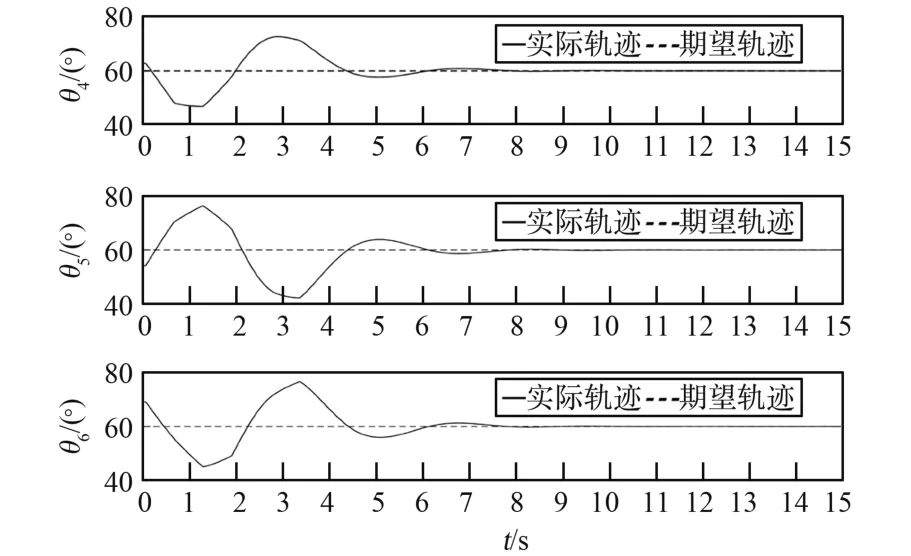
图7 右臂关节角轨迹Fig.7 Trajectory of right arm joint angles

结合图3、图4 可知,所提柔顺策略在电机循环4 次关停后将瞬时冲击力矩卸载,之后电机开始稳定输出,且整个控制过程均未出现瞬时冲击力矩超出关机阈值的情况。从图5～图7 可知,所提柔顺策略可实现失稳混合体系统的快速收敛,且具有较高的控制精度。

6 结论

1)在末端执行器与目标卫星发生剧烈碰撞时,所设计的SDD 可很好地降低关节所受冲击力矩,使空间机器人具备捕获高速、旋转卫星的能力。

2)配合SDD 设计的柔顺策略可在镇定控制过程中将关节所受瞬时冲击力矩限制在安全范围内,保护关节不受瞬时冲击载荷的破坏,有利于实现捕获操作过程的柔顺化。

3)分数阶超扭滑模控制可通过位置反馈对速度、加速度进行重构,解决了空间机器人无法测量速度、加速度信号的问题;所提算法鲁棒性强,收敛速度快,控制精度高,对混合体系统镇定控制具有一定的优势。