多优先级多车种动态应急交通网络反流策略研究

刘正，李新刚

(1.郑州航空工业管理学院，a.管理工程学院，b.航空经济发展河南省协同创新中心，郑州 450046；2.北京交通大学，a.交通运输学院，b.综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044)

0 引言

危化品爆炸泄漏和火灾爆炸等局部突发事件频发，一直困扰着社会安全。紧急转移受灾区域内人员至安全区域，同时，快速运输救灾资源至受灾区域是处置突发事件，保障受灾人员生命健康和财产安全的重要措施。道路作为重要的交通基础设施，应急区域路网的交通供给能力是有限的，承载着包括疏散车辆和救援车辆在内的不同优先级的多车种交通运行，有必要解决局部突发事件下多优先级多车种动态应急交通网络协调优化问题，平衡疏散和救援效果，满足激增的疏散和救援交通需求，具有重要的理论意义和实用价值。

突发事件下多优先级多车种在路网上交通运行优化研究方面，CHIU等[1]和杨兆升等[2]提出了多优先级疏散和救援交通组合优化的单目标数学规划模型，解决应急疏散和救援车辆在路网上同步动态交通分配的决策问题，但该模型以疏散和救援人员加权行程时间最短为目标，难以根据多车种之间的优先级差异保障救援车辆优先占用道路资源。XIE等[3]采用静态行程时间确定疏散交通运行过程中的应急交通路线，探讨了基于预留应急交通路线的区域疏散交通运行优化问题，但缺少考虑预留的路线应该随着路网交通状态(例如车辆密度)的动态变化而变化。KIMMS 等[4]以最小化不同危险水平道路上承载的疏散车辆数为优化目标，建立单目标混合整数线性规划模型，探讨了疏散和救援交通在路网上动态运行的组合优化问题，并通过设计分阶段优化方法确定疏散和救援交通运行优化方案，但无法保障救援交通优化效果。CUI等[5]以最小化疏散成本、救援成本、车流同时占用道路资源的冲突成本及车道反流成本这4项指标的加权值为目标，提出了最小费用流模型，优化疏散和救援交通在共享路网上的分配方案，但无法体现应急交通状态动态变化，无法保障救援车辆优先占用路网资源。LIU等[6]基于分阶段优化方法建立面向救援优先的多优先级疏散和救援交通运行优化的混合整数线性规划模型，研究了调整救援交通入口开放方案对疏散和救援交通优化效果的影响，但未控制不同优先级车种在交叉口的冲突转向对车辆通过交叉口的影响，路网资源未充分提供给应急车辆通行。LIU 等[7]和刘家林等[8]建立了大型和小型疏散车辆的车道分配与车队配置协调优化模型，解决多模式疏散交通协调优化问题，但未考虑优先通行的救援车辆及其对疏散交通的影响。

突发事件下多优先级多车种在路网上交通运行时，交通管制措施能够影响车辆在路网上的时空分布，有效利用稀缺的路网资源。突发事件下多优先级多车种交通管制研究方面，常用的措施包括交叉口转向控制和道路反流等。XIE等[9]建立疏散交通网络优化的双层规划模型，采用禁忌搜索算法和拉格朗日松弛算法求解，探讨了道路反流和交叉口冲突转向消除措施的协调优化问题。ZHENG等[10]基于系统最优原理研究疏散交通网络优化问题时，根据获取的疏散交通运行优化方案，采用交通仿真方式识别路网存在的瓶颈，利用道路反流和交叉口信号控制措施消除识别的瓶颈，返回优化模型重新优化疏散交通运行方案，直到疏散路网不存在瓶颈或者疏散效果没有进一步改善。HUA 等[11]研究了道路反流和交叉口冲突转向消除措施协调的疏散交通网络优化问题。YUAN 等[12]通过建立疏散交通管理优化问题的双层规划模型，研究了交叉口信号控制和冲突转向消除措施的协调优化问题。文献[9-12]探讨了车辆之间无优先权差异的单车种交通管制问题，缺少研究多优先级多车种在路网上通行的交通管制问题，未分析优先通行车辆的交通管制如何影响低优先级车辆交通运行，以协调优化整体的应急交通管理效果。相比于文献[9-12]，杨兆升等[2]研究了应急疏散和救援车辆在路网上通行时的交叉口应急控制和道路反流措施，但缺少考虑优先通行的救援车辆的反流策略如何影响低优先级疏散车辆的通行，无法平衡疏散和救援交通优化效果。

综上，对于局部突发事件下多优先级多车种动态应急交通网络协调优化问题，学者多从多车种角度进行研究，对多车种之间的优先级差异考虑不足。本文考虑优先通行车辆的反流策略占用让行车辆的道路时空资源，松弛路段传输模型，建立局部突发事件下多优先级多车种动态应急交通网络协调优化的多目标混合整数线性规划模型(Multiobjective Mixed Integer Linear Programming for Multi-Priority Multi-Class Dynamic Emergency Traffic Network, MPCDETN-MMILP)，设计分阶段求解算法，验证具体算例，分析救援车辆逆行路段数对疏散和救援交通的影响，实现疏散和救援效果的协调优化。

1 问题描述与建模

1.1 多优先级多车种动态应急交通网络协调优化问题

危化品爆炸泄漏和火灾爆炸等局部突发事件下，路网的交通供给能力是有限的，转移受灾人员的疏散车辆与运输救援资源的救援车辆同时在路网上运行时，两者具有相反的交通流向和不同的优先通行权：疏散车辆从受灾区域流向外部安全区域，救援车辆从外部救援场站(例如消防站和医院等)流向受灾区域；疏散车辆和救援车辆的交通路线冲突时，救援车辆享有优先通行权，疏散车辆应该等待或者绕行以避让救援车辆。在此情形下，多优先级多车种在动态应急交通网络上通行，采取道路反流策略提高救援交通流向的交通供给能力时，势必会影响疏散交通流向的道路通行能力。那么，局部突发事件下多优先级多车种动态应急交通网络应该如何实现协调优化，更好地平衡疏散和救援效果。

1.2 MPCDETN-MMILP模型

1.2.1 符号说明

(1)集合符号及其含义

Ω为动态交通仿真更新的时间步集合，Ω={1 ,2,…,T}；ψ为具有优先级差异的多车种集合，ψ={1 ,2} ；L为应急交通网络的所有路段集合；为路段i的下游相邻路段集合，i∈L,∈L；为路段i的上游相邻路段集合，i∈L,∈L；L·为疏散过程中，救援车辆占用的所有路段集合，L·⊆L；Λ(i,j)为疏散过程中，与救援车辆从路段i转向路段j冲突的交叉口转向集合，i∈L,j∈；Γ(i,j)为交叉口处，与从路段i转向路段j冲突的转向集合，i∈L,j∈；LP为 配 对 路 段 集 合，LP={i,n|i,n∈L} ，其中，路段i与路段n为连接相同的交叉口但交通流向相反的路段。

(2)参数符号及其含义

T为动态交通仿真的时间步总数，T= |Ω|；ℓ为动态交通仿真的时间步长(s)；α为不同优先级的各车种索引，α∈ψ，即α=1 表示救援交通，α=2表示疏散交通；li为路段i的长度(m)，i∈L；τi为交通自由流速度为vi时，车辆通过路段i所需的时间步数，τi=li viℓ，i∈L；ιi为路段i在交通拥堵状态下，拥堵交通的激波以速度wi从路段下游端传播到路段上游端时所需的时间步数，ιi=li wiℓ，i∈L；Qi为路段i的道路通行能力，i∈L；为路段i的交通阻塞密度，i∈L；Ed为疏散交通需求，表示从受灾区域内转移受灾人员的疏散车辆数；Rd为救援交通需求，表示从外部救援场站调用的到达受灾区域以处置突发事件的救援车辆数。

(3)决策变量及其含义

yi为0-1 变量，决策各路段反流策略，i∈L，yi=1 表示救援车辆在路段i上逆向行驶，yi=0 表示救援车辆在路段i上按正常方向行驶；为0-1变量，决策交叉口冲突转向，i∈L,j∈,α∈ψ，=0 表示禁止特定车种α从路段i转向路段j，=1 表示允许特定车种α从路段i转向路段j；计算第t个时间步内，从外部救援场站通过路段i进入应急交通网络的救援车辆数，t∈Ω,i∈L；计算第t个时间步内，从路段i离开受灾区域的疏散车辆数，t∈Ω,i∈L；计算第t个时间步内，从路段i进入受灾区域的救援车辆数，t∈Ω,i∈L；计算第t个时间步内，从应急交通网络通过路段i进入安全区域的疏散车辆数，t∈Ω,i∈L；为道路交通流量，计算第t个时间步内，从路段i转向路 段j的 疏 散 或 救 援 车 辆 数，t∈Ω,i∈L,j∈,α∈ψ；为道路交通状态，计算第t个时间步初，路段i上承载的疏散或救援车辆数，t∈Ω,i∈L,α∈ψ；和为累计交通流量，分别为截止第t个时间步末，累计流入和流出路段i的疏散或救援车辆数，t∈Ω,i∈L,α∈ψ。

1.2.2 目标函数

局部突发事件下，疏散车辆应该尽快将受灾人员从受灾区域转移至外部安全区域，以获得救助；救援车辆应该迅速到达受灾区域以处置突发事件，因此，构成MPCDETN-MMILP 模型的两个优化目标为

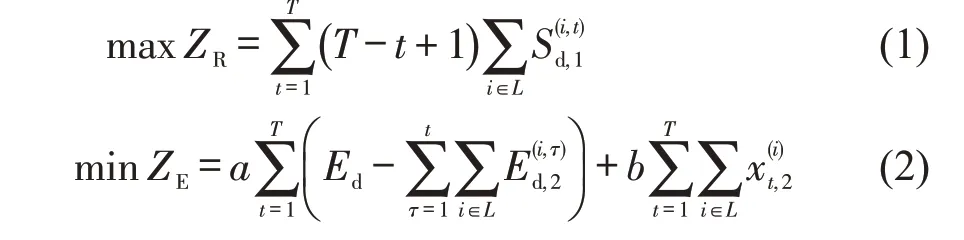
式(1)以时间为权重，以救援车辆尽快到达受灾区域为目标优化救援效果；式(2)以最小化滞留在受灾区域和应急交通网络上的疏散车辆数，使受灾人员尽快转移至安全区域为目标优化疏散效果，由以a和b为系数的两项构成：第1 项计算不同时间点滞留在受灾区域内的疏散车辆数，第2项计算不同时间点滞留在应急交通网络上的疏散车辆数。在式(2)中，a≥b表明，受灾人员更倾向于离开受灾区域，进入周围道路以远离灾害的威胁；a＜b表明，受灾人员更倾向于停留在受灾区域就地避险，直到进入应急交通路网能够提高疏散效果。

1.2.3 约束条件

求解式(1)和式(2)确定的局部突发事件下多优先级多车种动态应急交通网络协调优化问题，需满足如下约束式。

(1)动态网络交通流加载约束

疏散车辆通过应急交通网络从受灾区域到达安全区域，救援车辆通过应急交通网络从外部救援场站到达受灾区域，随着时间的推移，形成了多优先级多车种动态网络交通流，表现为道路交通量和交通状态是时变的，可采用广泛使用的路段传输模型[13-14]进行仿真，即

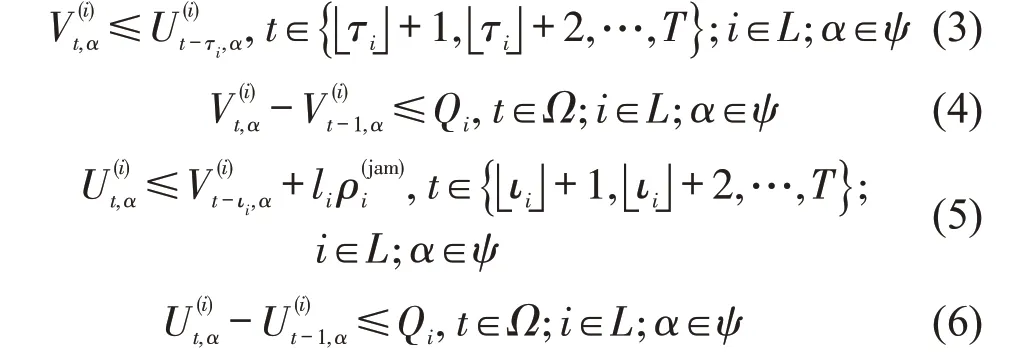
在任意时间步t(t∈Ω)内，进入和离开任意路段i(i∈L)的各车种车辆数应该满足约束为

式(7)和式(8)中，时间步t(t∈Ω)的取值范围为正整数，而截至任意时间步t+δ(t∈Ω,δ∈[0,1] )，累计进入和离开任意路段i(i∈L)的各车种车辆数可用线性插值法[6]计算，即

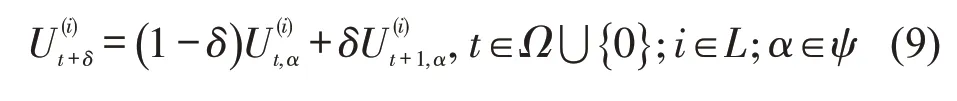
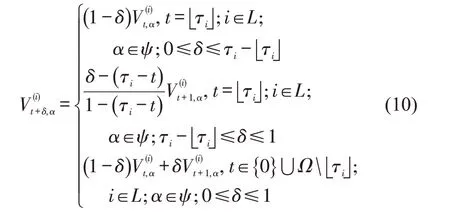
在任意时刻，任意路段上承载的车辆数应满足交通流量守恒条件：对于任意路段i(i∈L)，第t+1(t∈Ω)个时间步初承载的车辆数等于第t个时间步初承载的车辆数加上第t个时间步内进入该路段的车辆数，再减去第t个时间步内离开该路段的车辆数，即

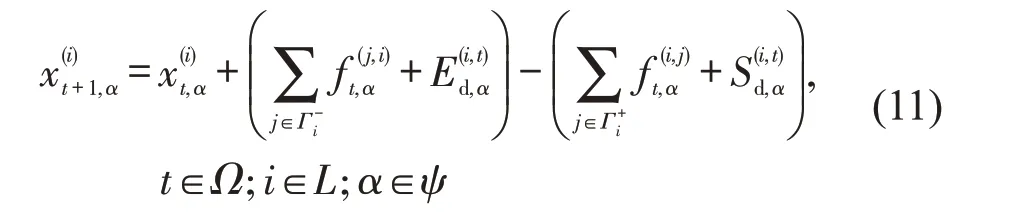
疏散和救援车辆在应急交通网络上通行时，应满足交通发生与吸引平衡条件：离开受灾区域的所有疏散车辆全部到达安全区域，从外部救援场站调用的救援车辆全部到达受灾区域，即

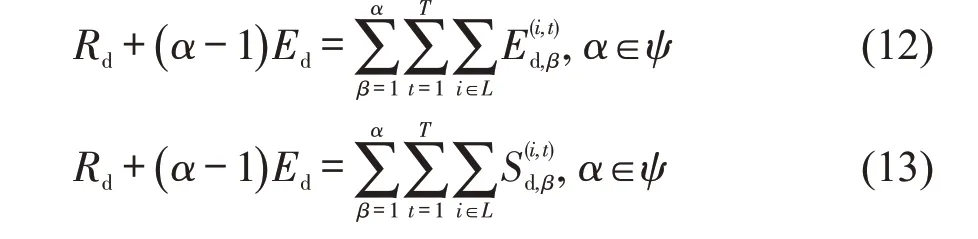
在多优先级多车种动态交通网络上，疏散车辆应该让行救援车辆直到救援车辆通过，即

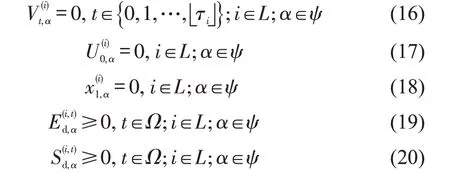
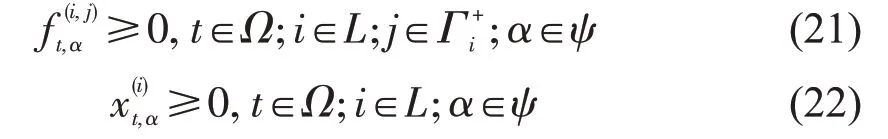
(2)交叉口冲突转向消除约束

十字形交叉口的冲突转向如图1所示。

图1 交叉口冲突转向Fig.1 Conflict turns at intersection

以从路段i到路段j的转向(i,j)与转向(r,n)存在冲突为例，采用交叉口冲突转向消除措施消除该冲突为

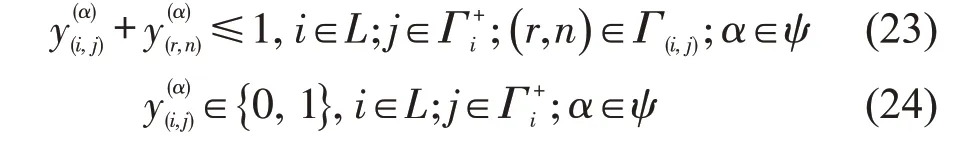
引入无穷大的数M，交叉口冲突转向消除与交通流量之间的量化关系为

(3)救援交通反流策略约束

道路反流表示将道路的正常交通方向调整为逆向通行，以提高相反方向的交通供给能力。以图1所示的配对路段i和n为例，道路反流策略为

以救援交通为例，如果反流策略在路段i的配对路段n被使用，则道路反流与交通流量约束为

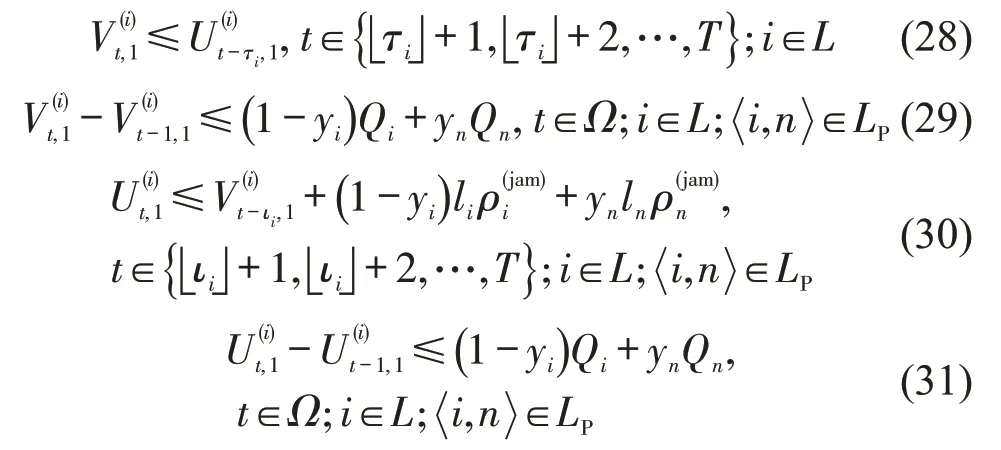
在式(26)～式(31)中，存在yi=0 和yn=1 且-＜Qi,i,n∈LP,满足约束的情况，意味着以MPCDETN-MMILP模型的最优解作为救援交通优化方案，当路段i被规划为按正常交通方向通行，路段i的配对路段n被规划为按反流方向逆行时，会出现不符合实际的情况占用疏散过程的道路通行能力，进入路段i的正常交通方向与配对路段n的逆行方向的救援车辆数低于路段i的道路通行能力。因此，作为救援交通反流路段的流量约束，表明路段i的配对路段n被规划为逆行路段时，在路段i的正常交通方向须有超过路段i的道路通行能力的救援车辆数(路段i的救援交通需求超过其交通供给能力)，即

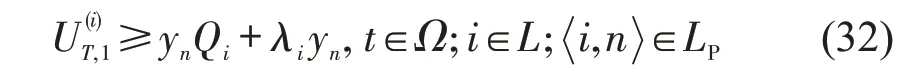
式中：对于任意路段i，λi∈N+均为给定的已知值。

在救援车辆优先通行情形下，救援交通使用逆行路段必然会占用疏散交通流向的道路通行能力。因此，有必要限制救援车辆占用的逆行路段数，以协调优化疏散和救援效果。救援交通逆行路段数约束为

式中：z为自然数，z∈N；z*为救援交通优化取得最优目标函数值时对应的逆行路段数限制。

考虑到救援车辆在路网上逆行会占用正常通行方向的道路，如果救援车辆在路段上i正常通行，在路段i的配对路段n上逆行(即yi=0 且yn=1，i,n∈LP)，则应该禁止疏散车辆在路网n的正常交通方向通行，直到救援车辆通过，即

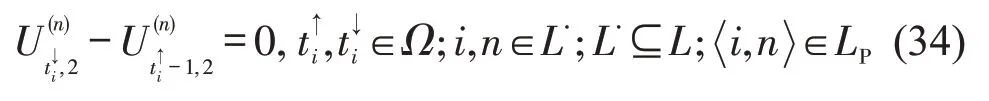
2 分阶段求解算法

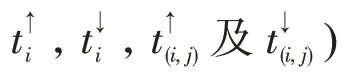
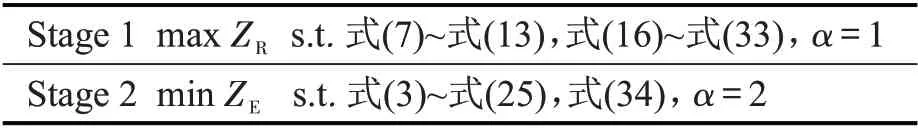
表1 MPCDETN-MMILP模型分解Table 1 MPCDETN-MMILP decomposition

求解MPCDETN-MMILP模型的分阶段优化方法流程为：

Step 1 不考虑救援车辆在多优先级多车种动态应急交通网络上可选的逆行路段数限制，调用Cplex求解器求解以式(1)为优化目标，约束为式(7)～式(13)、式(16)～式(32)的单目标混合整数线性规划模型，获取式(1)最优解对应的救援车辆占用的逆行路段数z*。

Step 2 以数值z*为式(33)中救援车辆可选的逆行路段数z的上界，以1为步长，逐渐减小救援车辆可选的逆行路段数z。

Step 3 判断数值z是否大于或者等于0。如果z≥0 成立，将z代入式(33)。采用分阶段优化方法求解表1所示的MPCDETN-MMILP模型的分解模型Stage 1 和Stage 2；如 果z≥0 不 成 立，跳到Step 7。

Step 4 调用Cplex 求解器求解以式(1)为优化目标，约束为式(7)～式(13)、式(16)～式(33)的单目标混合整数线性规划模型，求解救援车辆在多优先级多车种动态应急交通网上的优化问题，获取救援车辆占用的路段i(i∈L·)及时间[]；获取救援车辆占用的交叉口转向(i,j)及时间[] 。

Step 5 以Step 4 获取的救援车辆占用的路段和交叉口转向数据为输入，建立式(14)、式(15)及式(34)，禁止疏散车辆进入救援车辆占用的路段，禁止疏散车辆在交叉口的转向与救援车辆转向冲突，直到救援车辆通过。

Step 6 调用Cplex 求解器求解以式(2)为优化目标，约束为式(3)～式(25)和式(34)的单目标混合整数线性规划模型，求解疏散车辆在多优先级多车种动态应急交通网上通行的优化问题。返回Step 2。

Step 7 根据Step 4 ～Step 6获得的MPCDETNMMILP 模型的分阶段优化最优解，获取救援车辆选择不同的逆行路段数量时，疏散车辆和救援车辆在路网上的交通流量、交通密度及道路逆行方案。

求解算法如图2所示。

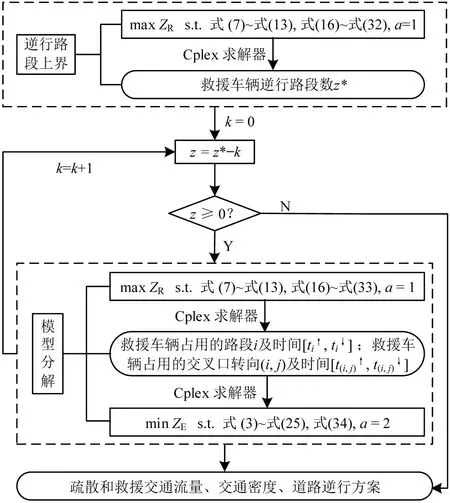
图2 MPCDETN-MMILP模型的分阶段求解算法Fig.2 Stage-based algorithm solving MPCDETN-MMILP model

3 算例分析

3.1 场景描述

为验证MPCDETN-MMILP模型与分阶段优化方法解决局部突发事件下多优先级多车种动态应急交通网络协调优化问题，平衡疏散和救援交通优化效果，本文选取研究动态交通网络配流具有代表性的Nguyen-Dupuis 路网[8]进行算例验证。Nguyen-Dupuis 路网由13 个交叉口节点和38 条路段构成，其中，路段1、路段2、路段9～路段16、路段27～路段32、路段37和路段38的长度均为200 m；路段3～路段6、路段19～路段26、路段35 和路段36的长度均为400 m；路段17、路段18、路段33 和路段34的长度均为500 m；路段7 和路段8 长度均为900 m；每条路段有2 个车道，道路通行能力为2160辆·车道-1·h-1，自由流速度为72 km·h-1，交通拥堵状态下的反向激波速度为18 km·h-1，交通堵塞密度为150辆·车道-1·km-1。虚拟路段无道路通行能力和交通阻抗限制。假设灾害导致的受灾区域位于节点1，4附近，安全区域与救援场站位于节点2，3 附近；受灾区域内的受灾人员借助540辆疏散车辆从节点1，4离开，从节点2，3进入安全区域；救援车辆从位于节点2，3附近的救援场站出发，从节点1，4 进入受灾区域，调用的救援车辆数为120辆，180辆；疏散和救援车辆在路网上运行的仿真总时长为600 s，路网交通状态更新的时间步长为10 s。路网如图3所示。

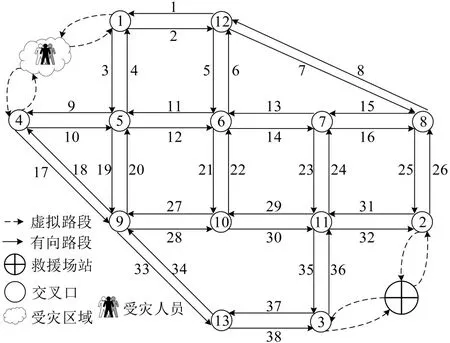
图3 Nguyen-Dupuis路网Fig.3 Nguyen-Dupuis traffic network

3.2 结果分析

3.2.1 多优先级多车种应急交通优化效果分析

选择分阶段优化方法求解MPCDETN-MMILP模型获得的最优目标函数值分析多优先级多车种应急交通优化效果。式(1)对应的最优目标函数值用来量化救援交通优化效果，该数值越大表示救援车辆更能迅速地到达受灾区域，对受灾区域的救援效果越好；式(2)对应的最优目标函数值用来量化疏散交通优化效果，该数值越小表示滞留在受灾区域和路网上的疏散车辆数越少，对受灾人员的疏散效果越好，其中，设定a=2，b=1 模拟受灾人员离开受灾区域和进入周围路网比滞留在受灾区域更安全。设置不同的救援交通逆行路段数限制，MPCDETN-MMILP模型获得最优解时救援车辆使用的逆行路段数如表2所示。

表2 救援交通逆行路段数表2 Number of contraflow links for rescue traffic

设置不同的救援交通逆行路段数限制时，MPCDETN-MMILP 模型的最优目标函数值如图4所示。

由图4可知，随着救援车辆使用的逆行路段数增加，救援交通优化的最优目标函数值逐渐增加，但这种变化趋势逐渐变缓，直到使用的逆行路段数增加至10 条时，最优目标函数值保持不变，表明：(1)救援车辆在路网上使用的最优逆行路段数存在上限。超过上限数量时，设置更多的逆行路段未必能使救援车辆更加迅速地到达受灾区域。在本算例中，该上限值在救援交通需求为120 辆车和180辆车时均为10。(2)增加救援车辆使用的逆行路段数未必能一直显著地提高救援车辆到达受灾区域的效率。

保障救援车辆在多优先级多车种动态应急交通网络上优先通行时，救援车辆使用逆行路段会明显延误受灾人员从受灾区域到达安全区域，降低疏散交通优化效果。如图4(a)所示，如果救援车辆无逆行路段使用(z=0)，疏散交通优化的最优目标函数值为9798；如果救援车辆使用逆行路段(z＞0)，疏散交通优化的最优目标函数值的最小值为10572(z=2)，最大值为11229(z=4)，超过数值9798 的比例分别7.9%和14.6%。此外，增加救援车辆使用的逆行路段数时，与救援交通优化不同，疏散交通优化的最优目标函数值整体上呈现增加的趋势，但这种趋势是波动式的，意味着调整救援交通逆行路段数也可以降低救援车辆优先通行对疏散交通的影响。

图4 疏散和救援交通优化的最优目标函数值Fig.4 Optimal objective function values in evacuation and rescue traffic optimization

以图4(a)为例，当救援车辆使用的逆行路段数从0条增加至10条时，救援交通优化的最优目标函数值从6318 增加至最大值6426，增加比例约为1.7%；疏散交通优化的最优目标函数值从9798 增加至11049，增加比例约为12.8%，意味着救援车辆使用逆行路段使救援交通优化效果提高1.7%时，会导致疏散交通优化效果下降约12.8%，是1.7%的7.5倍，显然，对疏散和救援交通优化效果的改善并不平衡。如果将救援车辆使用的逆行路段数从10条调整至3条，救援交通优化的最优目标函数值约增加1.0%，救援交通优化效果约降低0.7%，而疏散交通优化的最优目标函数值约降低8.4%，疏散交通优化效果约提高4.4%。因此，保障救援车辆在路网上优先通行时，调整救援交通逆行路段数能够平衡疏散和救援交通优化效果。

3.2.2 救援交通逆行路段选择情况分析

进一步分析不同的救援交通逆行路段数限制下，救援车辆对逆行路段的选择情况。设置不同的救援交通逆行路段数限制，MPCDETN-MMILP 模型获得救援交通优化的最优目标函数值时，救援车辆使用的逆行路段的编号如表3所示。

表3 救援交通逆行路段Table 3 Contraflow links for rescue traffic

由表3可知，当救援交通逆行路段数为1条时，救援车辆选择连接受灾区域且可构成最短径路(长度为1200 m)的路段17作为逆行路段，保障受灾区域入口有更多的交通供给能力提供给从周围路段汇集到此的救援车辆，使救援车辆迅速进入受灾区域；当救援交通逆行路段数为2 条时，连接外部救援场站，且可构成最短径路的路段25 也作为逆行路段，以提高连接救援场站的道路通行能力，使救援车辆尽快离开救援场站。随着救援车辆能够使用的逆行路段数增加，除了连接受灾区域和救援场站的更多路段(路段10，17，25，32和38)被规划为救援交通逆行路段外，中间路段(路段28，30 和33 等)也被规划为救援交通逆行路段，以匹配连接受灾区域和救援场站的道路的通行能力，提高救援车辆在路网上的通行效率。

设置不同的救援交通逆行路段数限制时，表3中的各逆行路段出现的次数统计如图5所示。

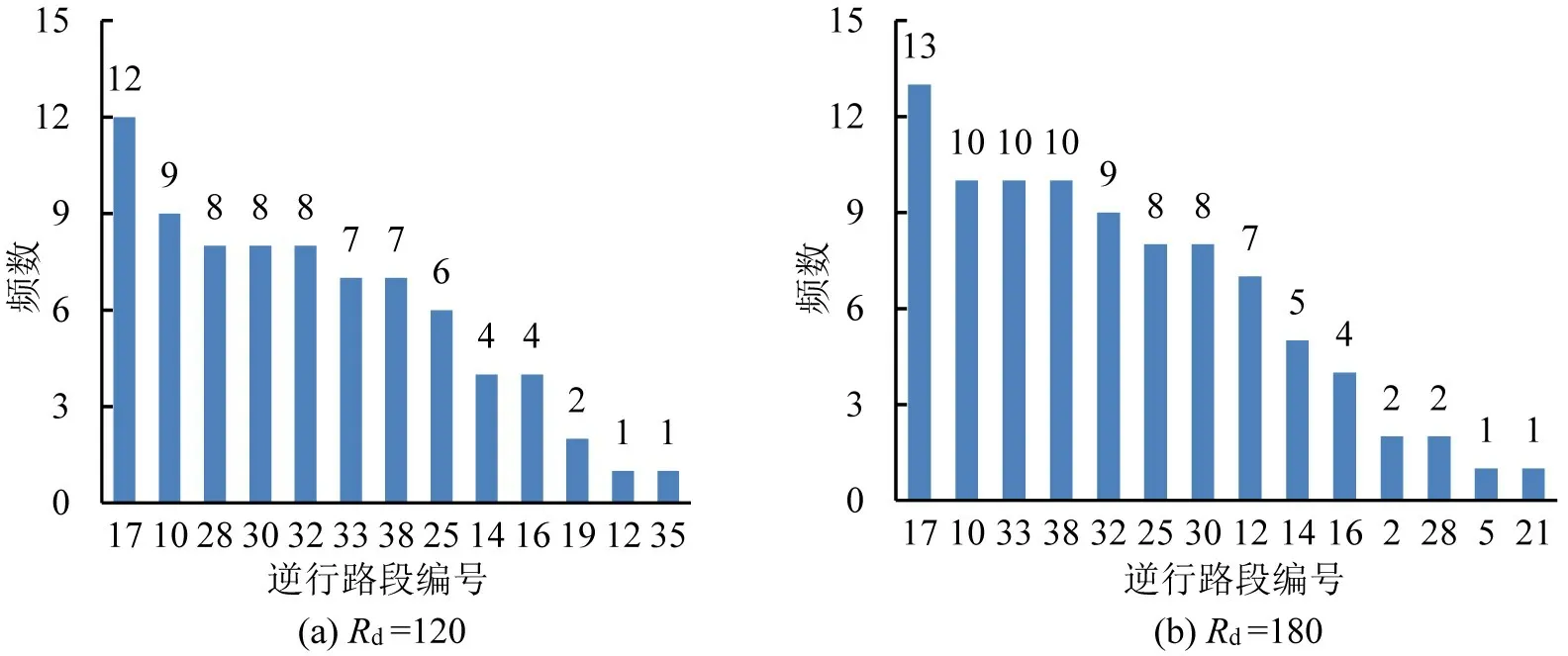
图5 救援车辆占用逆行路段的频数Fig.5 Frequency of contraflow links occupied by rescue vehicles

由图5 可知，首先，构成救援场站至受灾区域的最短径路，且连接受灾区域的路段10 和路段17出现的次数最多，表明在规划局部突发事件下的救援交通逆行路段时，可优先将连接受灾区域且能够构成最短径路的路段设置为逆行路段，以保障救援车辆从路网上迅速进入受灾区域。其次，连接救援场站且能够构成最短径路的路段32 和路段38，与中间路段且位于最短径路的路段30和路段33等出现次数最多，表明局部突发事件下，在满足救援交通逆行路段数限制条件下，也可将构成最短径路、连接救援场站的路段以及中间路段设置为救援交通逆行路段。

3.2.3 多优先级多车种动态交通分配分析

以救援交通需求为120辆车，救援交通逆行路段数为0 条和3 条为例，分析救援交通逆行路段数的设置对疏散和救援车辆在路网上动态交通分配结果的影响如图6 所示。在图6 中，箭头表示道路交通方向，路段上有3个数字：第1个数字表示未设置救援交通逆行路段时，求解MPCDETN-MMILP模型分配到各路段的交通量；第2个数字表示设置3条救援交通逆行路段时，求解MPCDETN-MMILP模型分配到各路段的交通量；第3个数字表示承载路段编号。

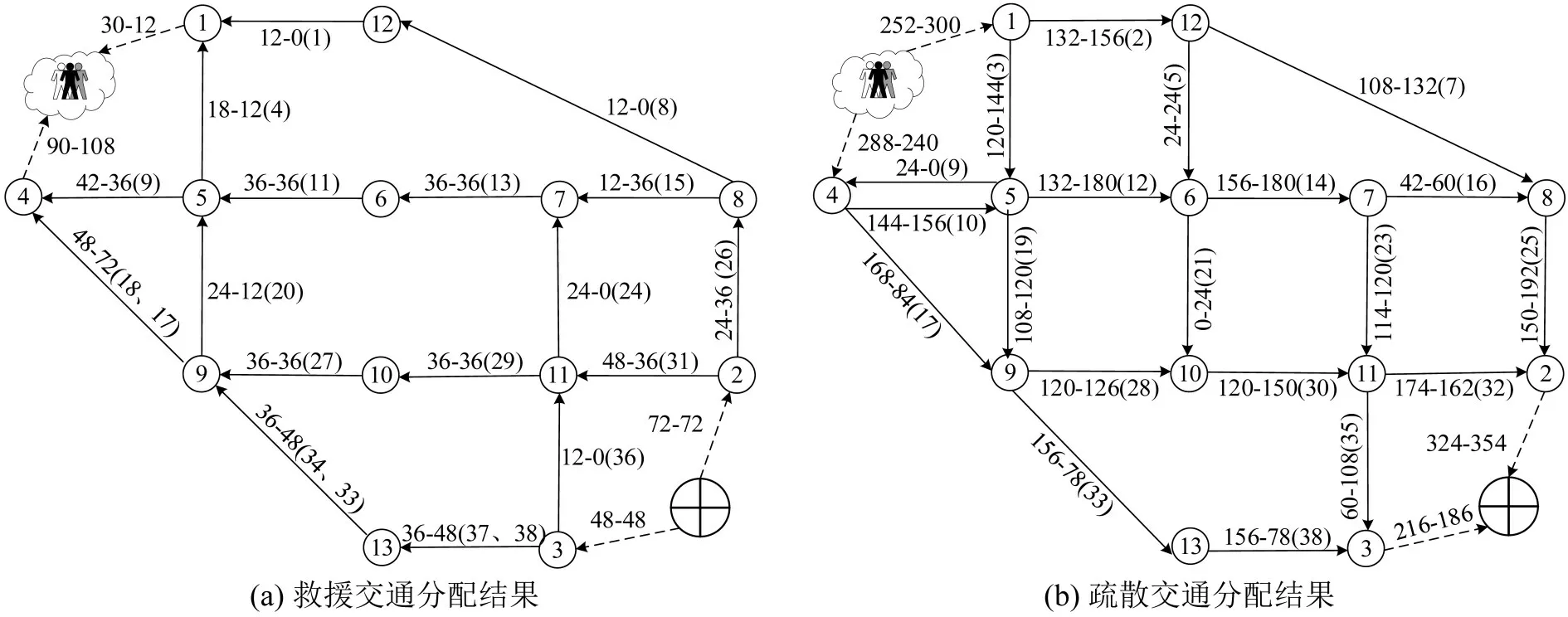
图6 多优先级多车种动态应急交通分配结果Fig.6 Multi-priority multi-class dynamic emergency traffic assignment results

如图6所示，在面向救援优先的疏散和救援动态交通网络上，给优先通行的救援车辆设置逆行路段提高交通供给能力时，会影响救援车辆在路网上的动态交通分配结果(图6(a))，而救援交通分配结果的变化会改变疏散车辆在路网上的动态交通分配结果(图6(b))。例如在图6(a)中，未设置救援交通逆行路段时，路径(以节点序列表示)：救援场站→2→8→12→1→受灾区域，救援场站→3→11→10→9→5→4→受灾区域，救援场站→3→13→9→4→受灾区域分别被分配了12，12，36辆救援车辆；设置3条救援交通逆行路段时，上述路径分别被分配了0，0，48辆救援车辆。显然，使用逆行路段17，33和38以增加救援交通方向最短径路(救援场站→3→13→9→4→受灾区域)的交通供给能力后，减少了使用非最短径路的救援车辆数，改变了救援车辆在路网上的动态交通分配结果。

从受灾区域至安全区域的最短路段序列径路17→33→38被规划为救援交通逆行路段时，疏散车辆由于让行救援车辆，会被禁止通行。在图6(b)中，设置救援交通逆行路段时，通过路径17→33→38 的疏散车辆数为84 辆，降至未设置救援交通逆行路段时分配的疏散交通流量的1/2，而未分配到最短径路17→33→38 的疏散车辆会被分配到其他更长的径路上，例如，节点序列路径：受灾区域→1→12→8→2→安全区域。因此，设置救援交通逆行路段使更多的救援车辆分配到较短的径路，会占用疏散交通方向的道路供给能力，进而影响疏散车辆在路网上动态交通分配结果，使更多的疏散车辆选择较长的径路。表明，在局部突发事件下多优先级多车种动态应急交通网络上采用反流策略时，有必要考虑优先通行的救援车辆的逆行路段数对疏散交通分配的影响，这种影响可通过本文提出的MPCDETN-MMILP模型与分阶段优化方法优化与规划。

4 结论

基于本文提出的解决局部突发事件下多优先级多车种动态应急交通网络协调优化问题的MPCDETN-MMILP 模型与分阶段优化方法，算例验证得到的主要结论如下：

(1)随着救援交通逆行路段数增加，救援车辆到达受灾区域的速度的增加趋势逐渐变缓；而让行的疏散车辆在受灾区域和路网上转移受灾人员的速度总体上呈现下降趋势，这种趋势是波动式的。优化救援交通逆行路段数能够降低救援交通优先通行对受灾人员疏散效率的干扰。

(2)救援车辆逆行路段数及对救援车辆迅速到达受灾区域的提升存在上限，会持续影响受灾人员在受灾区域和路网上的疏散效率。在本算例中，能够提升救援交通优化效果的逆行路段数上限为10 条。超过10 条后，救援交通优化的最优目标函数值保持不变，疏散交通优化的最优目标函数值仍会改变，意味着规划更多的逆行路段未必能使救援车辆更迅速地到达受灾区域，但能够改变受灾人员的疏散效果。

(3)保障救援车辆在路网上优先通行时，限制救援交通逆行路段数能够平衡疏散与救援交通优化效果。在本算例中，将逆行路段数由10 条调整为3 条时，救援车辆到达受灾区域的效率约降低0.7%，而疏散车辆转移受灾人员的疏散效率约提高4.4%。

(4)在救援车辆逆行路段数限制下，为使救援车辆能够迅速到达受灾区域，可优先将连接受灾区域且能构成最短径路的路段规划为逆行路段，然后，是连接救援场站且能构成最短径路的路段，最后，是能构成最短经路、匹配受灾区域与救援场站交通供给能力的中间路段。

(5)设置救援交通逆行路段会使更多的救援车辆分配到最短径路，占用疏散交通方向的道路供给能力，进而导致更多的疏散车辆转移到较长的径路。