基于有限穿越可视图的进场航班流量波动特性研究

张勰，肖恩媛，刘宏志，赵嶷飞，王梦琦

(1.中国民航大学，空中交通管理学院，天津 300300；2.中国民航科学技术研究院，民航发展规划研究院，北京 100028)

0 引言

掌握空中交通流量涨落波动特性对于优化空域资源配置、提升运行效率、保障飞行安全能够发挥先导性、基础性、关键性作用。研究空中交通流波动动态态势有助于理解整个空域交通系统的运作原理与演化机制，同时是设计有效空中交通流量管理措施与控制策略的基础，也为空中交通流量演变建模仿真与预测提供一种新的思路。

针对交通流特性方面的研究，Mayara Condé Rocha Murça等[1]提出数据分析框架，实现高保真地描述空中交通流。Sidiropoulos 等[2]提出一种框架用于分布式鲁棒优化方法的研究，探究多机场终端区空域空中交通流的运行模式。2014—2016年，张洪海等[3-4]分别采用建模仿真工具等方法研究终端区空中交通流量、密度和速度参数之间的动态演化关系。随后，张洪海等[5]提出相应TOD(Transitoriented Development, TOD)模式下的进场交通流优化模型，结果表明，该模型能够有效化解终端区潜在的航路冲突，并且能够保持交通流安全高效地运行。针对交通流特性方面的研究，大多数研究从非线性特性出发，或仅基于单一的时间尺度，仅在静态层面反映交通流的真实特性，很少从时空层面考虑交通流的动态特性。

针对时间序列内在特征方面的研究，王超等[6]研究了一种基于改进加权一阶局域法的混沌交通流量时间序列预测模型。Weinreich 等[7]采用小波分解方法开展预测计算，进而研究预测对于时间序列在不同时间尺度上所表现出来的依赖性。张弦等[8]提出一种基于嵌入维数自适应最小二乘法支持向量机的预测方法，实验表明，该方法适用于航空发动机状态时间序列的预测。随后，张弦等[9]提出一种基于支持向量机经验模态分解的预测方法，结果表明，该方法能够实现对故障率的准确预测。针对时间序列分析，当前的空中交通时间序列主要关注空中交通运行过程预测和因果分析，缺乏空中交通系统运行动态的分析研究。

针对空中交通流波动特性的研究，刘宏志等[10]将复杂网络理论引入到时间序列的应用当中，使用Motif理论提取波动模式，结果发现，时间序列中存在显著的波动模式以及这些波动模式之间的转换循环。围绕机场空中交通流量时间序列的复杂性问题，张勰等[11]在引入多个粗粒化的过程中，提出一 种 改 进 的 MMPE(Multivariate Multiscale Permutation Entropy,MMPE)方法，有助于深入了解空中交通系统的演化机制，从而揭示时间序列多尺度复杂性的剧烈波动。随后，刘宏志[12]从交通流波动动态演化、波动多尺度分形特征和多尺度复杂性的角度探讨流量短期及长期的演变规律。针对空中交通流波动特性的研究成果较少，且当前研究仅使用较为简单和直观的方法进行实验，未考虑实验结果的真实性和普适性。

为从时间维度考察空中交通的动态演化，本文面向3个时间粒度，采用有限穿越可视图方法将进场航班流量时间序列映射成复杂网络，分别从网络整体统计特性和网络局部结构模式两个视角开展研究，为从多粒度多维度刻画流量时间序列的波动特性提供分析方法和理论工具。

1 航班流量时间序列

按照中国民航空管流量管理运行规则[13]。扇区流量统计方法，分别基于2018 年12 月1 日当日以及2018 年12 月1 日～31 日整月天津机场进场航班流量数据(6:30-23:50)，采用5，10，20 min 时间间隔统计3个时间粒度的航班流量时间序列，长度分别为208、104 和52，如图1 所示。航班当日流量时间序列为

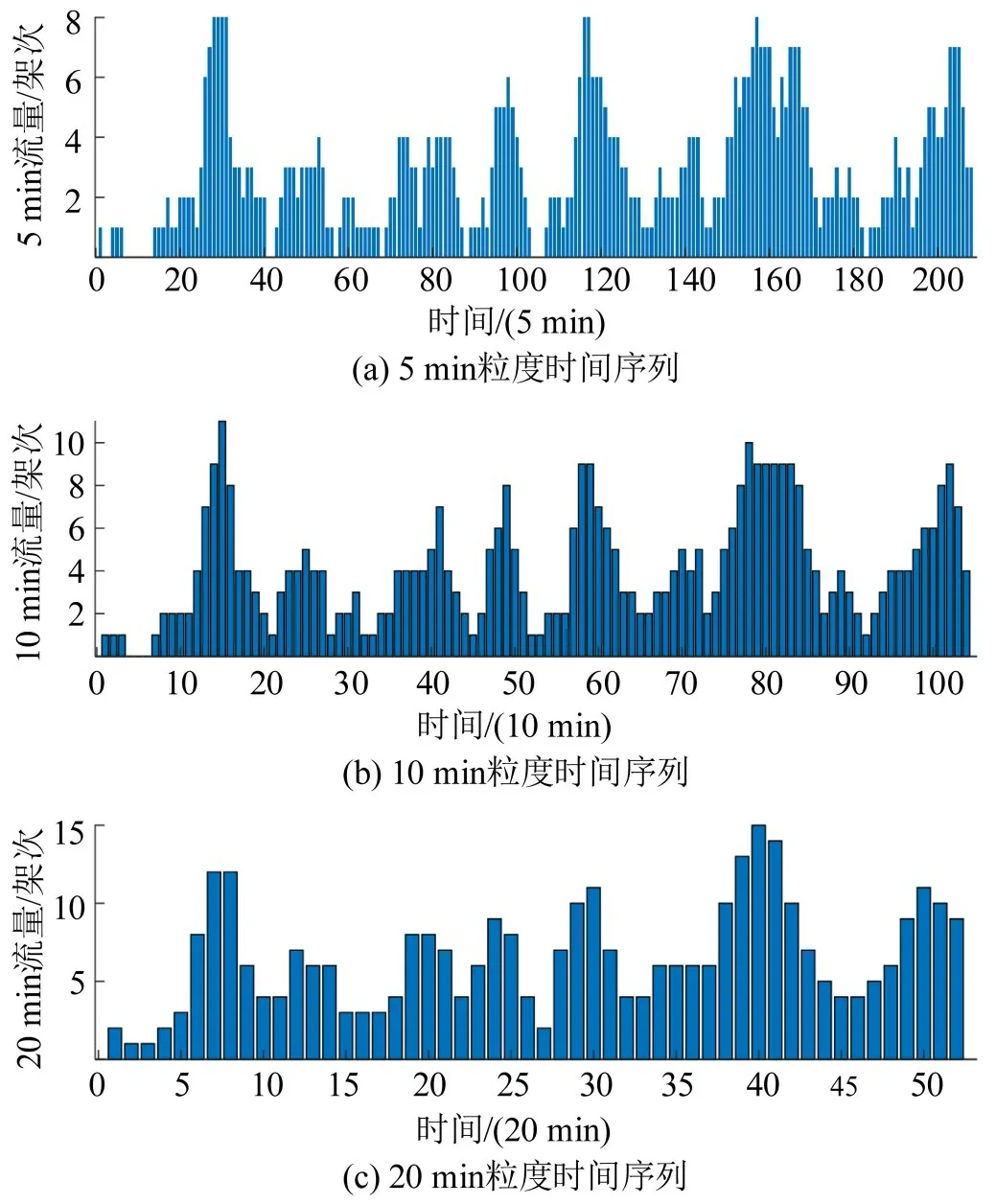
图1 天津滨海国际机场进场航班流量时间序列Fig.1 Arrival flight flow volume time series of ZBTJ

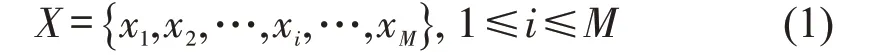
式中：xi为第i个时段内终端区进场流量；M为时间序列长度。

2 面向整体特征的流量波动统计特性分析

2.1 有限穿越可视图

随着复杂网络的快速发展以及获得的丰硕成果给时间序列分析提供了崭新的视角，将复杂网络方法与时间序列分析相结合也为进一步研究实验对象的动力学特征提供了新的思路。在时间序列映射为复杂网络的诸多方法中，可视图方法以方便与直观等特点多次被使用，可视图方法无需人为添加参数，且映射之后的节点与时间序列存在一一对应关系，同时复杂网络分析的实验结果可以直接用于分析时间序列的真实属性和特征，因而可视图方法用于分析时间序列特性非常实用与高效。

可视图(Visibility Graph, VG)和水平视图(Horizontal Visibility Graph,HVG)都能有效地刻画空中交通流时间序列波动特性[10]，在此基础上，有限穿越可视图方法[14](Limited Penetrable Visibility Graph,LPVG)显示出独特的优势，近些年被广泛应用于各个领域。周婷婷等[14]对3 种可视图网络(可视图、水平可视图、有限穿越可视图)考察时间序列建网方法对周期、分形、混沌以及添加噪声信号后的适应能力。Liu等[15]采用有限穿越可视图和相空间方法将EEG(Electroencephalogram)序列映射成网络，研究AD(阿尔茨海默病)大脑潜在的混沌系统动态学。Ming Z.等[16]对有限穿越可视图进行抗噪测试，结果证明，有限穿越可视图具备优于传统可视图的抗噪能力。Ren等[17]将有限穿越可视图与序模体方法结合，结果证明，有限穿越可视图序模体方法有良好的鲁棒性，并且提出可以应用于挖掘水包油两相流超声波传感器信号中包含的不同流信息。

有限穿越可视图定义了穿越距离N。若时间序列中两节点连线截断的数目d(即被其他节点截断的个数)满足d≤N，则两个节点可连通[18]。这表明，当两个节点之间的连接视线被截断的次数不超过有限次数N时，两个节点之间是存在有效可穿越可视线的。当N=1 时，有限穿越可视图样例如图2所示，图中，实线是合格的有限穿越可视线，虚线是不合格的情况(d≥2)。

图2 LPVG示意图Fig.2 Schematic of limited penetrable visibility graph

参数N的设置能够有效地减少噪声对时间序列可视线的影响，具有比VG 和HVG 更好鲁棒性[14,16]。同时，LPVG 也提高了可视图的整体相关性，改善了网络节点的聚类效果，对时间序列的波动适应性更强。因此，本文采用有限穿越可视图方法分析进场航班流量时间序列波动特性。

针对有限穿越可视图N值的设置情况，N越大，允许穿越的节点数量就越多，时间序列节点之间的整体关联性就会越强，但是选择过大会相对弱化相邻节点的关联性。

航班流量时间序列采用有限穿越可视图方法进行建网，再构造序模体，对序模体转移概率进行实验数据分析，VG序模体转移概率方差为0.07967以及LPVG(N=1～3)的3 组方差(0.04980、0.05189和0.07147)，4 种情形可视图序模体方差最小值为LPVG的N=1 情况，且能够低于其他3组网络平均0.01790。

因此，本文采用N=1，即只允许穿越一个节点，不仅能在合理提升整体节点关联性的同时最大程度上保留可视图局部结构的原貌，同时能够满足构造有限穿越序模体时局部波动能处于一个稳定状态。

2.2 流量时间序列的整体统计特性

3个时间粒度流量时间序列映射得到LPVG 1，LPVG 2，LPVG 3，如图3 所示，其统计特性如表1所示。

表1 LPVG网络统计特征Table 1 Network statistic characteristics of resulting LPVGs

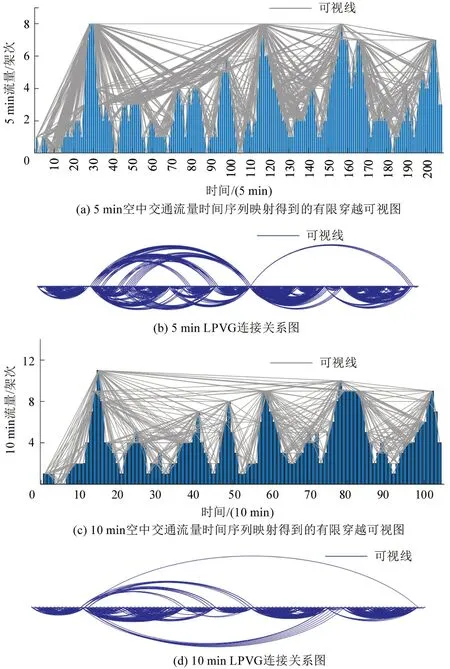
图3 空中交通流量时间序列映射得到的有限穿越可视图Fig.3 Limited penetrable visibility graphs mapped from flight flow volume time series

理论研究表明，可视线密度的变化反映了航班流量的波动，这是因为航班流量的增减起伏导致可视线连接关系的变化，从而引起相应节点可视线密度的改变。而k-core 算法利用节点的度刻画单个节点的连接关系，旨在利用core值大小刻画航班流量波动强弱。

综上，可用k阶核量化流量的波动强度，其算法定义为：对于图G=(V,L)，V为节点，L为连边，定义n= |V|,m= |L|，W为节点集合，则定义子图H=(W,L|W)当且仅当∀D_V≥k(D表示节点度)，V∈H，且H是一个具有这样属性的最大子网络时，称H为节点集合W诱导的一个k阶核。各节点所属核的阶数为其所能参与的最高的k阶。该算法能够得到节点度不小于k的最大子网络。

根据该算法得到各个聚类簇如图4所示，相应的统计结果如表2～表4所示。

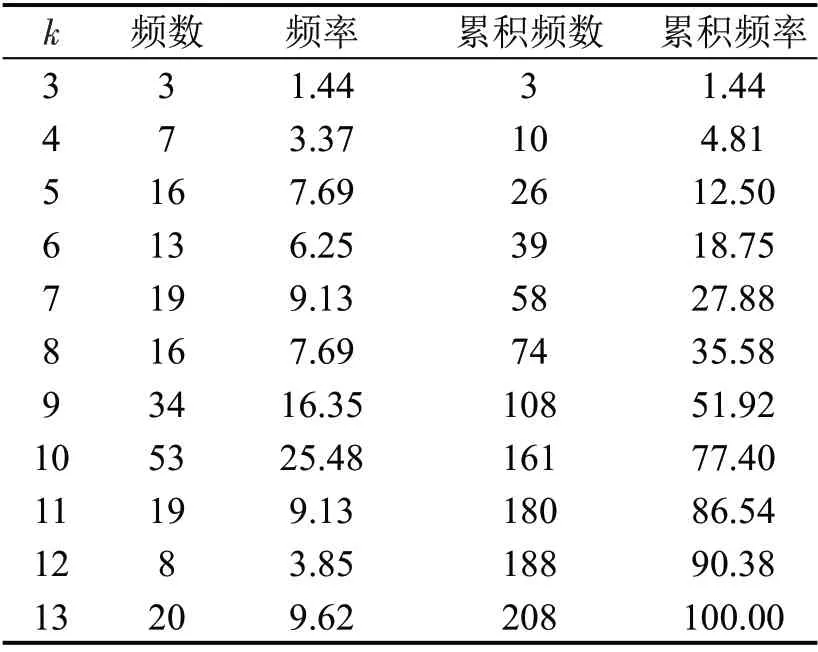
表2 LPVG 1统计特性Table 2 Statistic characteristics of LPVG 1

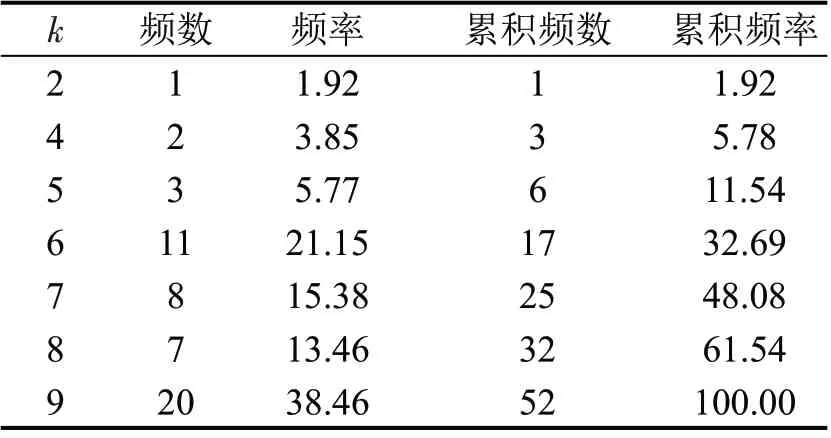
表4 LPVG 3统计特性Table 4 Statistic characteristics of LPVG 3

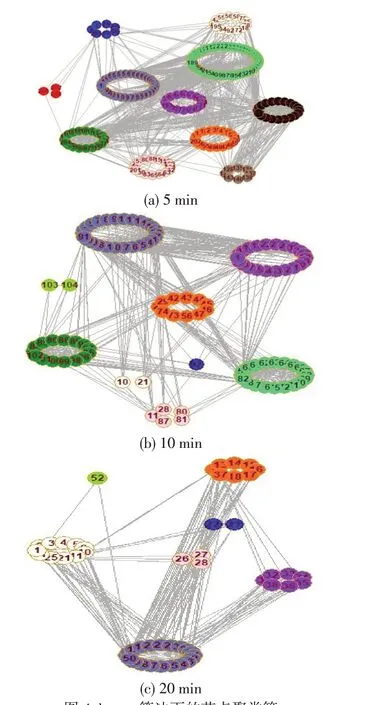
图4 k-core算法下的节点聚类簇Fig.4 Clusters of nodes with k-core

表3 LPVG 2统计特性Table 3 Statistic characteristics of LPVG 2

可视线密度刻画航班流量波动强度，图4和表2～表4 说明，k-core 算法下随着时间粒度变大和可视线密度降低，核阶数种类变少、最高频数核阶数数值变小，同时聚类簇数量变少导致能够反映的波动区域也随之变少。因此，k-core算法对于有限穿越可视图网络可视线密度的变化尤为敏感，该算法对于利用有限穿越可视图方法建网刻画时间序列波动特性具有良好的适应性。

图5给出当日各时段所对应节点的k阶核数变化趋势图。k阶核趋势随着时间粒度变大而变得平缓，峰值变小，所表征的流量波动强度随之减弱。基于上文仅针对一日流量数据，为了得到更精确的天津机场进场航班流量时间序列整体波动态势，其分析计算步骤如下。

图5 当日k 阶核变化趋势Fig.5 Trend of k-core on that day

(1)统计2018年12月1日～31日相同时段航班流量数据并采用LPVG 连接关系，利用k-core 算法得出相应阶数。

(2)一个月的节点阶数为

(3)一个月的流量平均值为

(4)绘制计算结果如图6所示。

图6 时间序列整体波动态势Fig.6 Overall fluctuation trend of time series

随着时间的变化，时间序列流量柱呈现高低起伏态势，这种变化趋势通过可视图可视线可以有效且准确地表征。流量柱高低起伏越大，即流量柱在一定时间范围内高度变化幅度较大，此时节点拥有的可视线数量也在不断变化，因此用节点可视线密度来表征这种时间序列波动的情形。

综上所述，波动的一般描述性定义为：在一定的时间段内随着时间的变化，流量柱呈现高低起伏的变化态势，并且这类变化可以用可视图可视线密度有效且准确地表征，我们称这类变化为波动。

利用复杂网络k-core 方法计算分析可视线密度进而表征时间序列波动强度，本文统计2018 年12月1日～31日相同时间段节点k-core平均数值，随后针对得到的3 种时间粒度1 个月的实验结果，分别按照5，10，20 min步长求取一个60 min内所有节点k-core 总和最大的时段，按照k-core 总和排序可以得到以下结果。

①5 min时间粒度对应k-core总和最大的区域为15:25-16:25，其次为16:25-17:25，最后为16:30-17:30，如图6(a)虚线连接部分；

②10 min 时间粒度对应k-core 总和最大的区域为16:50-17:50，其次为17:00-18:00，最后为17:10-18:10，如图6(b)虚线连接部分)；

③20 min 时间粒度对应k-core 总和最大的区域为14:10-15:10，其次为15:30-16:30，最后并列为16:30-17:30和16:50-17:50，如图6(c)虚线连接部分。

综上，用复杂网络k-core方法计算分析可视线密度进而表征时间序列波动强度，k-core 数值越大，则表征的时间序列波动强度越强。因此，强波动时段的判定标准为：利用k-core算法计算分析流量时间序列节点可视线密度，节点k-core数值最大的区域能够刻画该时间序列的强波动时段。

纳入标准：①身体健康，无全身性疾病；②无代谢性骨疾病、无放化疗病史；③无未治愈的牙周炎；④缺牙时间≥3个月；⑤吸烟≤10支/d；⑥牙槽骨条件满足种植要求，术中无须植骨；⑦能保持口腔卫生，依从性好，知情同意。

根据上述3种时间粒度k-core总和排序得出的6个时段，其3种时间粒度公共时段为16:50-17:30，即天津滨海国际机场进场航班流量强波动时段为16:50-17:30。

通过结合实际运行场景，流量值持续较大或者持续较小的时段会导致时间序列节点的可视线连接数量过少，因为节点周围没有过高或者过低的节点与之相连，从而实验结果为该时段航班流量波动强度较弱。反之，航班流量数值变化较大，存在短时内航班流量数值出现较大的差异时，可视线数量多，可视线密度大，该时段的航班流量波动较强。通过可视线连接关系及k-core 数值变化刻画航班流量时间序列节点的波动特性，利用波动特性为实际运行中进场航班流量削峰填谷管理策略提供一种全新的思路。

3 基于局部结构的流量波动动态演化分析

Shen-Orr S. S.等[19]提出模体(motif)概念，Iacovacci等[18]受其启发提出序模体概念，在此基础上，Ren 等[17]提出有限穿越可视图序模体。在有限穿越可视图节点按时间顺序排列的情况下，构造一个滑动窗口，依序滑动，在每个窗口中得到的网络子结构(即子网络)就是一个有限穿越可视图序模体。

通过LPVG 映射得到的3 个可视图网络，使用有限穿越可视图序模体(简称序模体)考察可视图的局部结构模式。由于本文中可穿越数N=1，故时间序列两节点之间只相隔一个节点的可视线必定存在，这表明要刻画波动模式的差异需要4节点以上长度的序模体。

3.1 频繁序模体类型

图7 列出了流量时间序列当中出现的各长度序模体的不同类型，4、5 和6 节点序模体出现的类型总数分别为2 种、6 种和34 种。图7 中，仅列举4节点和5 节点可能存在的流量柱连接关系的示意图。图7 当中4、5 和6 节点序模体，节点对应于流量波动研究的指标是时间序列的流量柱，在流量波动研究当中流量柱是具有高度的“柱子”，如图7中柱状图所示，图中横坐标表示时间轴，纵坐标表示流量值，在序模体的研究中流量柱被看作是大小相同的节点，这是为了更好地刻画不同连接关系的序模体类型，便于研究分析网络局部结构的流量波动动态演化规律。

对照图7 连接关系进行分析。按照有限穿越可视图规则以及N=1 设置可以分析得出，节点依次排列对应现实场景航班流量随时间而起伏变化，序模体中存在的连接线对应有限穿越可视图当中的可视线，当两个节点存在可视线则说明两节点存在以下两种可能。

图7 流量时间序列中出现的序模体类型Fig.7 Sequential motif types presented in flow time series

①两个节点可见，分为相邻可见和不相邻可见，此时必然存在可视线，如图8实线。

②两个节点不可见，但是中间障碍物数量为1(满足N=1条件)，此时也存在可视线，如图9实线。

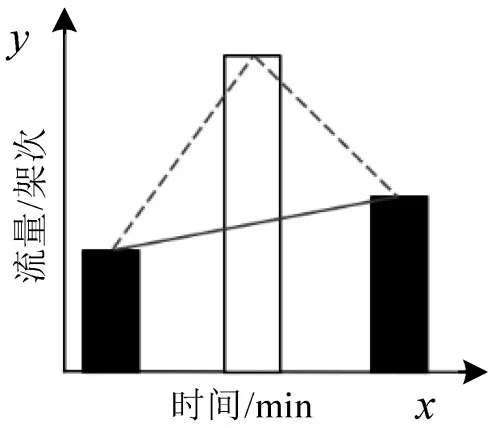
图9 两个节点不可见示意图Fig.9 Schematic diagram of two nodes invisible

当存在可视线时，对应于空管实践场景如下。

①针对第1 种可能，两个节点可见必然存在相邻可见关系或是不相邻可见关系，如图8(a)所示。这两种情形对航班流量管理研究者而言，只要存在两种可见关系其中任意一种，可以通过调整连接线两端的节点航班流量数值达到对进场航班流量的精准调控，从而避免拥挤和资源浪费。

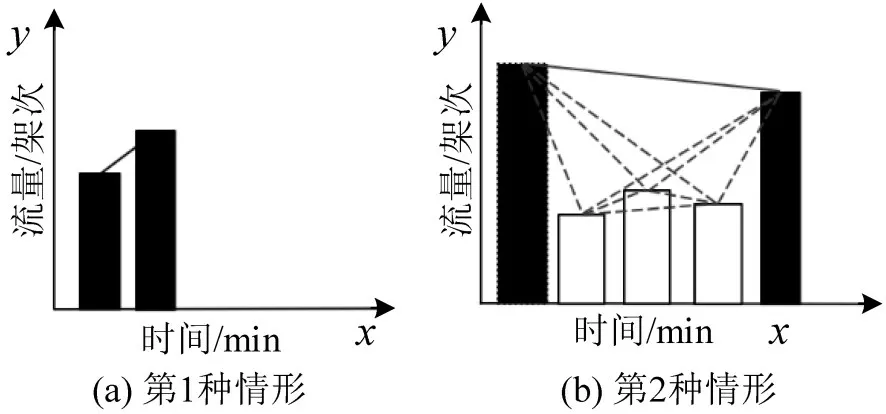
图8 两个节点可见示意图Fig.8 Schematic diagram of two nodes visible

②针对第2种可能，两个节点不可见，但是中间障碍物数量为1的情形，可以作为第一种可能的备选调控方案。当直接可见节点的航班流量面临调整遇到棘手问题，如调整数值达到上限等情况，可以采取第2 种备选方案，即第2 种可能。利用有限穿越可视图N=1 的缓冲限制达到对现实场景航班流量精准调控的目的。

3.2 流量波动模式的动态转换

波动模式动态转换图步骤如下。

(1)将流量时间序列中每一个时间点上的空中交通流量视为一个节点，节点之间的连接关系由有限穿越可视图中的可视线准则确定。

(2)分别按照4、5、6节点宽度设置滑动窗口，移动步长为1，当滑动窗口移动经过所有节点，则得到时间序列中出现的所有序模体。

(3)将不同序模体类型作为波动模式动态转化图中的不同节点，按照滑动窗口的移动所体现的类型转换关系，绘制不同序模体类型之间的转换方向，即波动模式动态转化图中相应节点之间的有向边，当滑动窗口完成在整个时间序列上的移动后，即可得到空中交通流量波动模式动态转化图。

通过上文对波动的概念阐述，流量柱的可视线密度变化能够直接表达流量时间序列的波动情况，但是对于序模体而言，原文旨在从网络局部角度来探察波动演化特性，利用序模体不同类型的动态转移刻画流量波动演化规律，其过程为：流量柱看作节点→探察序模体类型(可视线连接关系)→考察序模体转移概率(不同连接关系的变化)→序模体转换概率图(连接关系变化图)。

综上，序模体的不同类型能够对应流量柱的起伏变化情况，流量柱的起伏变化必然与可视线密度的大小变化相关联，可视线密度的变化能够引起流量时间序列的波动变化，探察序模体类型的转移能够有效刻画航班进场流量时间序列的波动转移模式。

3个时间粒度的波动模式动态转化图如图10～图12 所示。图中，节点大小和数字代表序模体的不同类型，节点大小与度成正比，包括本节点的出度与来自图中其他节点的入度，也包括该节点本身上的自环。自环就是系统状态从同一种模式转换到同一种模式，即在同一个节点上的转换，动态演变模式是没有变化的。本质上，在自环前后，系统状态并没有发生变化，是系统状态的保持。线条宽度代表转移的频次(同一序模体之间的对比)，即线条越宽序模体之间的转移频次越多。由于4 节点的序模体只有两种类型且两种类型之间转移次数几乎相同，这里仅绘制5 min 时间粒度4 节点序模体转换图。

图10 5 min粒度的LPVG中4节点模体序转换图Fig.10 4-node sequential motif transitions in resulting LPVG(5 min)

图12 6节点序模体转换图Fig.12 6-node sequential motif transitions in resulting LPVGs

表5 为在不同单位尺度下每种模式的统计特征，包括每种类型出现次数和转移次数的均值(μ)和标准差(σ)。表5 中，同一时间粒度的不同序模体之间，序模体长度越大转移次数越少，转换类型总数变多，μ和σ越小。不同时间粒度的相同长度序模体之间，转换次数会越少，类型总数不变，μ和σ越小。

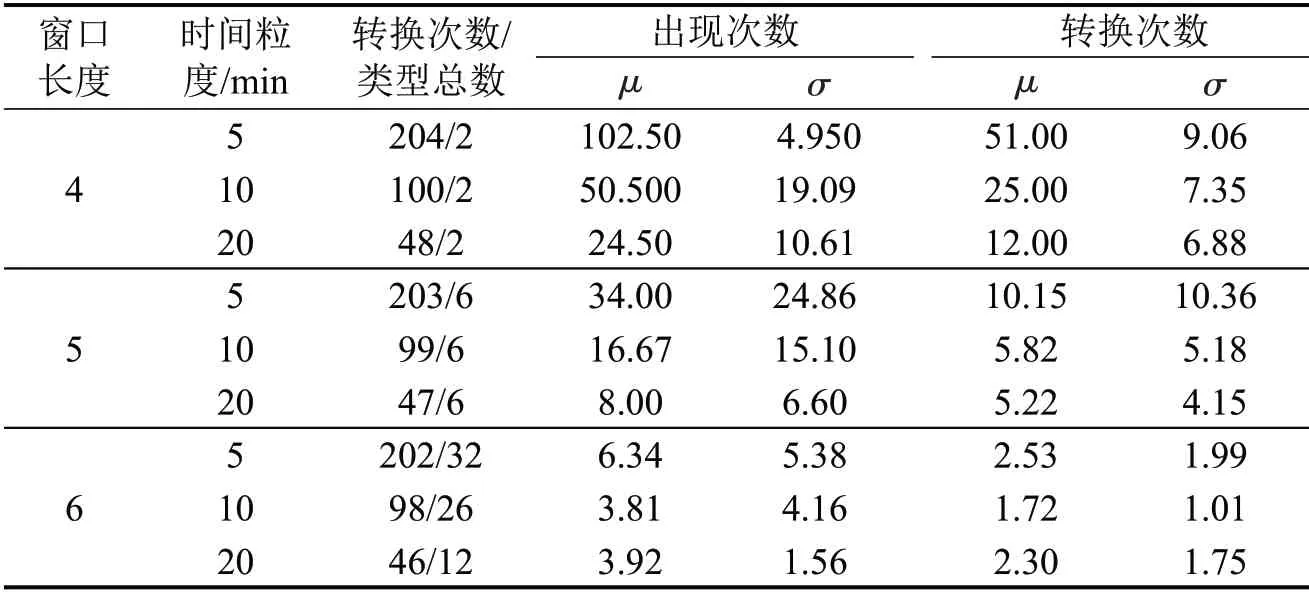
表5 序模体动态演化的统计特征Table 5 Statistical characteristics of sequential motifs dynamic evolutions

通过将序模体看作节点，将不同类型之间的转换映射成网络，有效地刻画了空中交通流量序模体的动态演变。图11和图12中不同宽度连边构成的序模体转换环路，也为空中交通流量序模体模式的预测提供了有效途径。每一种转移环路可以通过图中箭头表达，连边的宽度表示转移的次数。基于此，可以得到序模体转移矩阵。表6～表9列举4节点和5节点不同尺度下的序模体转移矩阵。表6中(2,1)位置值为44，代表全天流量中序模体类型从01转移到02转换了44次。

图11 5节点序模体转换图Fig.11 5-node sequential motif transitions in resulting LPVGs

表6 LPVG 4节点波动模式转移矩阵Table 6 Transition matrix of LPVG 4-node fluctuation patterns

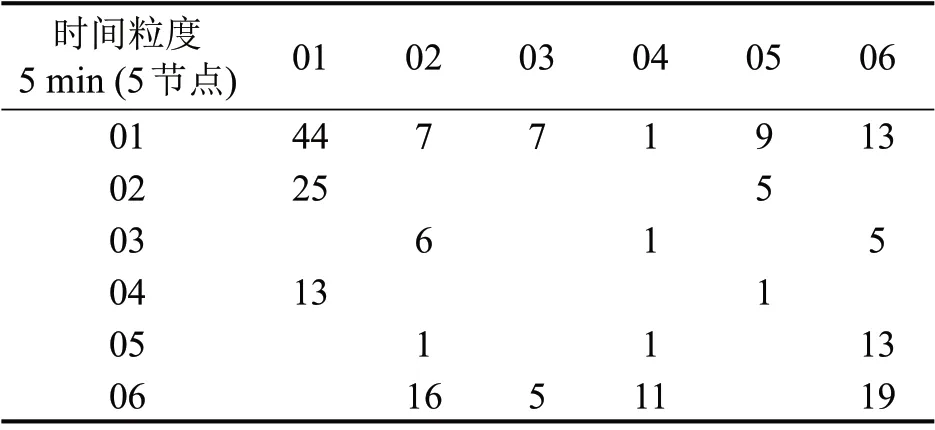
表7 5 min时间粒度LPVG 5节点波动模式转移矩阵Table 7 Transition matrix of LPVG 5-node fluctuation patterns with 5-minute time granularity

表8 10 min时间粒度LPVG 5节点波动模式转移矩阵Table 8 Transition matrix of LPVG 5-node fluctuation patterns with 10-minute time granularity

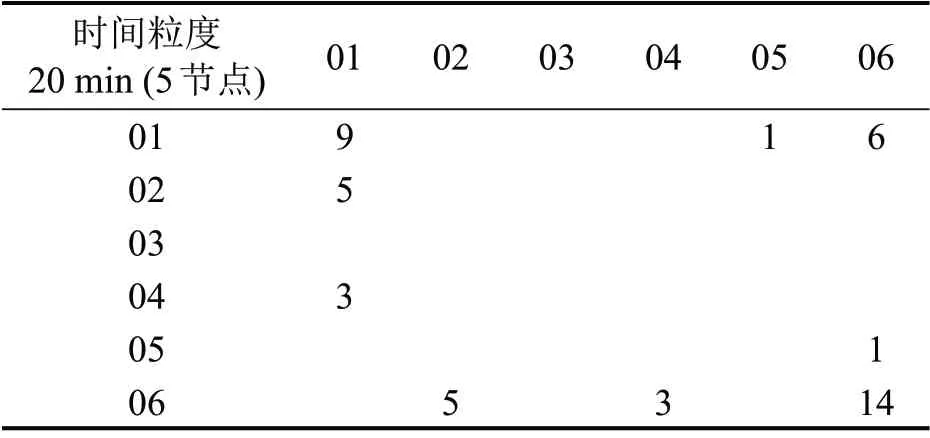
表9 20 min时间粒度LPVG 5节点波动模式转移矩阵Table 9 Transition matrix of LPVG 5-node fluctuation patterns with 20-minute time granularity

5 节点粒度的时间序列中，4 节点序模体模式01 向模式02 转换了44 次，转移概率为44/204=0.22。针对转移概率，分别对4，5，6 节点序模体绘制矩阵图，如图13～图15所示，通过深浅变化(颜色越深频率越高)可以明显观察到各种类型序模体之间的转移频率。

图13 4节点序模体矩阵图Fig.13 4-node sequential motif matrix diagram

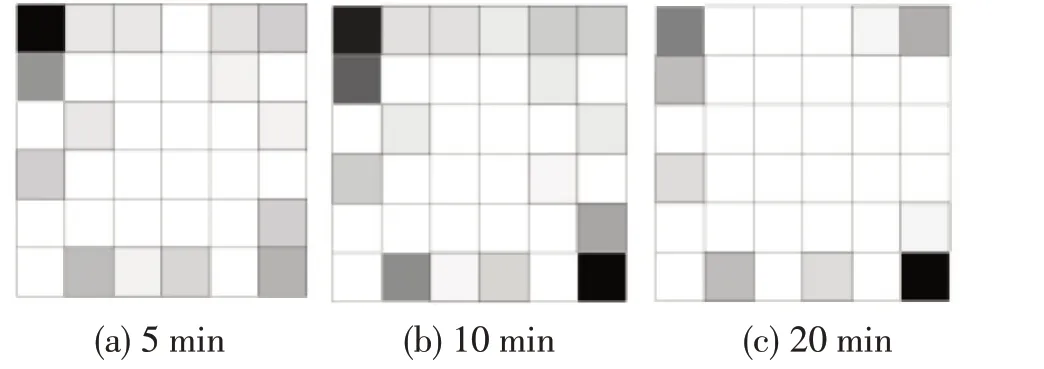
图14 5节点序模体矩阵图Fig.14 5-node sequential motif matrix diagram

图15 6节点序模体矩阵图Fig.15 6-node sequential motif matrix diagram

序模体矩阵图对角线上的数字是节点的自环数。图13 中颜色的深浅程度表明4 节点的类型1向类型2转移与类型2向类型1转移概率没有明显的差异，这说明4节点序模体转移矩阵刻画能力十分有限，推荐使用更长的序模体。5 节点和6 节点序模体转换概率如图16和图17所示。

图16 LPVG 5节点序模体转换概率图Fig.16 Transition probability graphs of 5-node sequential motifs in LPVGs

图17 LPVG 6节点序模体转换概率图Fig.17 Transition probability graphs of 6-node sequential motifs in LPVGs

在5 节点序模体矩阵图中，除去对角线自环，以下为序模体主要转移模式(转移概率大于0.10)。

(1)5 min为类型2—类型1(0.12)；

(2)10 min 为类型2—类型1(0.13)，类型6—类型2(0.10)；

(3)20 min 为类型1—类型6(0.13)，类型2—类型1(0.11)，类型6—类型2(0.11)。

对于6 节点，除去对角线自环，以下为序模体主要转移模式(转移概率大于0.03)。

(1)5 min为类型1—类型2(0.04)；

(2)10 min为类型1—类型2(0.05)，类型13—类型34(0.04)，类型14—类型1(0.04)，类型34—类型26(0.04)；

(3)20 min 为类型1—类型2(0.04)，类型2—类型10(0.04)，类型2—类型11(0.09)，类型10—类型34(0.04)，类型11—类型34(0.07)，类型14—类型2(0.07)，类型15—类型1(0.04)，类型25—类型14(0.09)，类型28—类型15(0.07)，类型34—类型25(0.09)。

5 节点序模体共有6 种，不同时间粒度下主要转移模式(转移概率大于0.10)一共有6 种。6 节点序模体共有34 种，不同时间颗粒下主要转移模式(转移概率大于0.03)一共有15 种。5 节点和6 节点能够通过序模体表现出空中交通流动态转移模式，但对于6 节点而言，由于序模体转移类型过多，且主要转移模式次数过少，导致序模体类型转移的识别不够明显，转换概率过低。而5 节点能够在6 种序模体类型下表现出良好的识别能力，有效刻画空中交通流波动动态转移模式。

根据以上序模体之间的转换关系研究可知，序模体越长，可以得到的模体种类越丰富，但序模体过长在空中交通混沌特性的影响下对于预测没有意义。因此，在研究空中交通流波动特性中，推荐使用5节点序模体。本文空中航班流量5节点序模体转移概率最高的转换模式为类型2—类型1，3种时间颗粒的转移概率分别为0.12(12.315%)、0.13(13.131%)和0.11(10.648%)。

序模体方法得到的不同序模体类型可以有效刻画空中交通流量的波动模式，同时根据序模体出现的顺序和频次抽取得到空中交通流量波动动态演化轨迹，如图16和图17所示，在图中可以非常清晰地看到由于不同宽度连边构成的模式转移环路，在实际运行中，探究进场航班流量波动模式的动态转换，有助于实际场景下流量管理方法的有效实施，同时为流量波动模式的预测提供了有效途径。

4 结论

本文得到主要结论如下：

(1)将k-core 算法与有限穿越可视图建网方法相结合探究航班流量时间序列波动特性得出，可视线密集程度与k阶核数值呈正相关，航班流量时间序列k阶核数值越大波动强度越大，天津机场进场航班流量数据的强波动时段为16:50-17:30。这表明，网络节点所属核阶数可以有效刻画流量的波动强度，能够从网络整体结构反映航班流量波动动态特性，为航班流量建模仿真与预测提供一种新的思路和方法。

(2)序模体过长在空中交通混沌特性的影响下对预测没有意义，针对航班流量波动动态演变的研究，5节点长度的序模体具有良好的适应能力，在3种不同时间粒度下转换形式为类型2—类型1，转移方向按照航班流量时间序列从左往右，转换次数为25、13 和5，转移概率为12.315%、13.131%和10.638%。有限穿越可视图序模体能有效表征多元序模体转换的动态演化规律，也表明，波动模式演化图具有潜在的应用价值，为波动模式的预测提供了有效工具。