基于非均匀发车间隔的大小交路时刻表优化模型

张海，吕苗苗*，倪少权

(西南交通大学，a.交通运输与物流学院；b.综合交通运输智能化国家地方联合工程实验室；c.综合交通大数据应用技术国家工程实验室，成都 610031)

0 引言

随着城市轨道交通线网形成，客流需求不断增大。高峰时段断面客流过于饱和，个别车站特别是换乘站因客流量过大存在车门多次开闭的情况，导致本趟列车及后续列车晚点，晚点列车会进一步加剧乘客在站台的集聚，构成潜在的安全隐患，给乘务部门造成较大压力。如何精细化适配列车运力与乘客需求、提高乘客出行体验是城市轨道交通急需解决的问题。

城市轨道交通自动售检票系统为基于客流需求的列车时刻表优化提供了数据支持。史峰等[1]提出基于时刻表的客流分配方法，在乘客服务水平限制条件下实现OD时变需求与列车时刻表耦合，以车底数最少为目标优化城轨列车运行计划。冉昕晨等[2]基于地铁客流空间分布，结合各区段列车负载率和列车运动方程，建立以静能耗最小为目标的列车时刻表优化模型，并设计二分法和粒子群算法对模型进行求解。李晓娟等[3]以增加铁路企业收益及精确匹配乘客出行需求为目标，基于既有列车运行图建立双层协同优化模型，实现基于定制化列车的运行图优化方案。宿帅等[4]提出疫情期间以降低列车满载率为优化目标的双层规划优化模型，在车辆资源有限的前提下基于客流需求优化列车运行图，并用CPLEX软件求解模型。NIU等[5]提出基于乘客时变需求及列车跳停场景的时刻表优化方法，以最小化乘客等待时间为目标函数建立混合整数非线性规划模型，并用GAMS 软件对问题进行求解。ZHU等[6]充分考虑乘客需求，以降低乘客等待时间和旅行时间为优化目标，提出城市轨道交通列车时刻表优化双层规划模型，并用遗传算法求解。SHI 等[7]以最小化乘客等待时间为目标函数，建立整数线性规划模型，通过优化列车时刻表及客流量控制策略，减少站台乘客集聚、提高服务水平，并设计启发式算法求解模型。WANG 等[8]考虑换乘站内乘客走行时间，基于时变客流对相邻线路时刻表进行协同优化，以降低总能耗及乘客旅行时间。XIE等[9]建立基于乘客需求的时刻表及停站方案协同优化混合整数规划模型，以降低列车能耗、增强运行图的鲁棒性，并设计并列选择遗传算法对模型进行求解。YANG 等[10]建立非等间隔时刻表优化模型，对乘客出行时间和能耗值进行协同优化。

基于城市功能布局、居民职住分离现状及轨道交通线路客流分担比例，多数线路客流呈现明显的早晚高峰特性。现行列车时刻表通常为不同时段的等间隔时刻表，早晚高峰时段采用较小的开行间隔。既有基于乘客需求的时刻表研究对象大多为相应时段的等间隔时刻表，部分文献对非等间隔时刻表进行了研究，但没有考虑到列车发车间隔不均衡对乘客的影响。城市轨道交通车站客流密度函数非均匀分布，等间隔时刻表不利于运力与客流需求的精确匹配，而非等间隔时刻表列车发车间隔不均衡性过大又会对乘客体验产生不利影响。本文以乘客平均旅行时间及列车发车间隔平均偏离值为协同优化目标，建立高峰时段基于非均匀发车间隔的大小交路时刻表优化模型，以最大限度地满足客流需求、提高乘客体验。

1 问题描述

考虑如图1 所示双线轨道交通线路，上、下行共设置2I个站台，站台F为小交路折返站台，列车在首站进行站前折返，在尾站及小交路折返站进行站后折返。列车集合为K；车站集合为Z；运营时段集合为T；k为列车标识；i,r,j为车站标识。

图1 轨道交通线路示意图Fig.1 Schematic of track layout of an urban rail transit line

开行大、小交路情况下，由于上、下行方向列车建模无本质差别，本文考虑下行方向车流，上行方向车流可按同样的方法进行推算。令Kl、Ks分别为大交路列车与小交路列车集合；Zl、Zs分别为下行方向大交路与小交路列车途经车站集合、Zn为下行方向大交路与小交路非共线区段集合，即Zl={1,2,…,I},Zs={1,2,…,F},Zn={F+1,F+2,…,I}。

传统等间隔时刻表中列车在车站的停站时间固定。固定的停站时间对客流量较小的车站而言，空耗了运力；对客流量较大的车站而言，其往往不能满足上、下客需求甚至造成列车晚点。本文将列车停站时间与上、下车乘客数量相关联，构建高峰时段基于非均匀发车间隔的大小交路列车时刻表优化模型，以更精确地匹配乘客需求、提高列车运行效率。考虑到列车发车间隔不均衡对乘客体验的负面影响，模型对乘客平均旅行时间及发车间隔平均偏离值进行协同优化。

根据城市轨道交通线路实际运营情况，对本文模型做如下合理性假定：

(1)所有运营列车车型、编组数相同。列车在每站都停车，不存在区间及站间越行场景。

(2)所有乘客在折返站台下车后，列车开始进行折返作业。

(3)到站乘客采用“先到先服务”原则。乘客不能乘坐当前列车时，需在站台等待下一次列车。

(4)本文研究对象为给定车次数及大小交路开行比例下的时刻表优化问题，研究时段内列车平均发车间隔及大小交路列车开行比例为一既定值。

2 非等间隔列车时刻表优化模型构建

2.1 模型变量

本模型的决策变量为hk,i及，前者为第k次列车追踪列车(k+)与其在车站i的发车间隔；后者为第k次列车在区间[i,i+1]的运行时间；中间变量为车次k在车站i的停站时间。

设定运营组织上开行2∶1 大、小交路，始发站(第1站)以3列列车为一个组合(前2列为大交路列车，第3 列为小交路列车)滚动发车。由于大、小交路列车运行区段及所服务车站不完全一致，追踪列车k+的车次号(发车序号)与车次k并不总是相邻。车次号为3n+1 及3n+2 的列车(n∈N)属于大交路列车，车次号为3n(n∈N+)的列车属于小交路列车。hk,i计算式及列车k+的车次号为

2.2 约束条件

(1)列车停站时间、运行时间及发车间隔约束

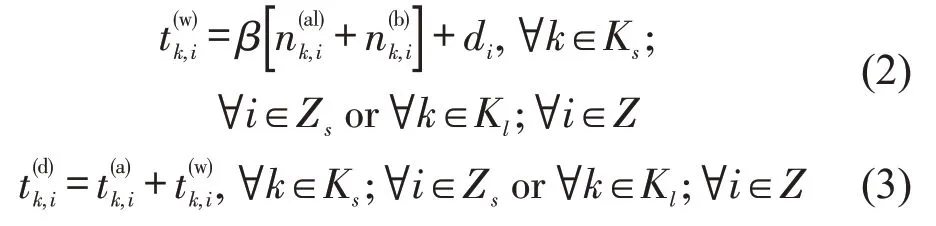
式(2)为列车停站时间约束，列车在车站的停站时间正比于该站上、下车乘客数。式(3)表示车次k驶离车站i的时间为车次k到达车站i的时间加上其在车站i的停站时间。

式中：Tstart为首次列车从首站发出时刻；Q为研究时段内发出的总车次数；Have为列车平均发车间隔；Tend为最后一次列车最晚发车时间。

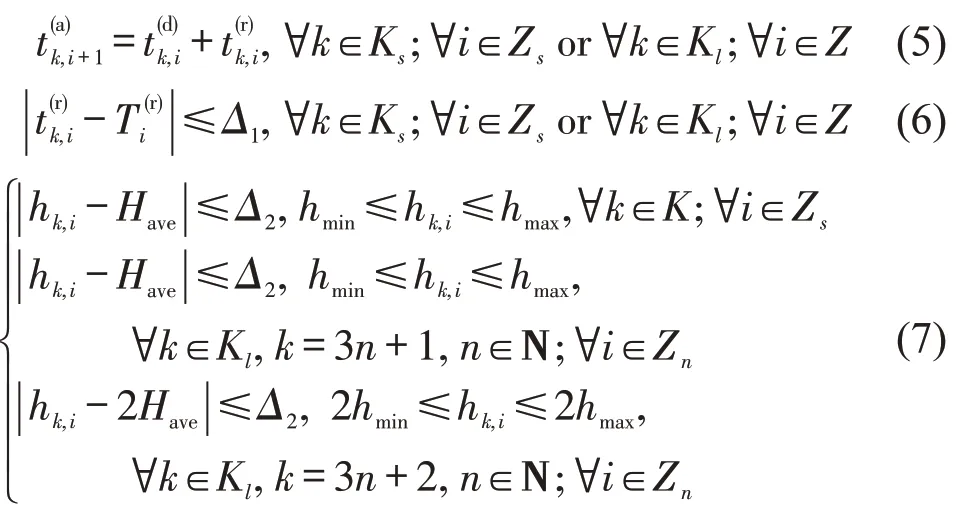
式(5)表示车次k到达车站i+1 的时刻为车次k离开车站i的时刻加上其在区间[i,i+1]的运行时间。式(6)为列车区间运行时间偏离约束。式(7)为列车发车间隔约束，优化后列车发车间隔值应在相应限定范围，且相较于等间隔发车间隔偏离值应在Δ2内。

(2)大、小交路列车相关约束

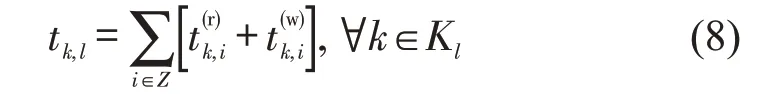
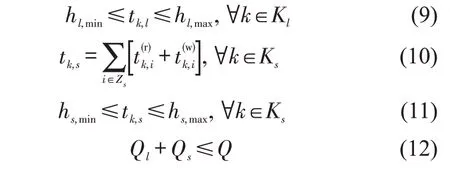
式中：tk,l为大交路列车下行总运行时间；hl,min、hl,max分别为大交路列车下行最短、最长运行时间；tk,s为小交路列车下行总运行时间；hs,min、hs,max分别为小交路列车下行最短、最长运行时间；Ql为大交路投入车次数；Qs为小交路投入车次数；Q为总车次数。式(12)为列车车次数约束。

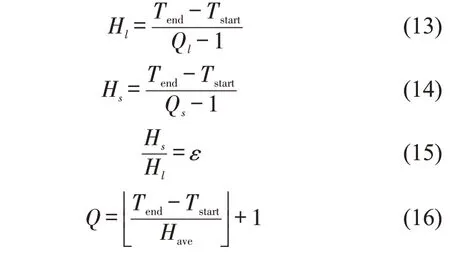
式中：Hl为大交路列车平均发车间隔；Hs为小交路列车平均发车间隔；ε为大、小交路列车开行比例。式(13)～式(16)为发车间隔相关联等式，其中，式(16)为总车次数计算式，既定研究时段及平均发车间隔下，列车总车次数为一定值。

(3)列车载客量及负载率相关约束

列车驶离车站时载客量与其到达车站时载客量及车站上、下车乘客数有关。

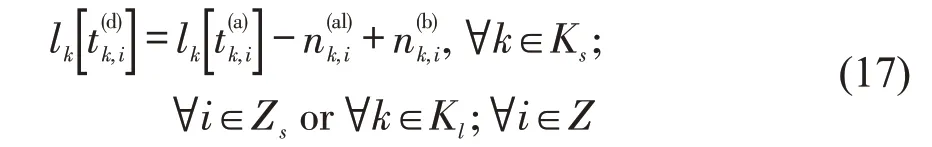
式中：lk[] 为车次k驶离车站i时载客量；lk[为车次k到达车站i时的载客量；为车次k在车站i下车乘客数；为车次k在车站i上车乘客数。

大、小交路列车路径下，根据乘客OD 情况，可将客流细分为3类。

第1 类：OD 起讫点均在小交路区段内(O,D∈Zs)的乘客可乘坐大、小交路列车，乘客无乘坐偏好，选择乘坐当前到站列车。

第2 类：如当前到站列车为大交路列车，跨交路乘客{O∈Zs(≠F),D∈Zn} 均选择乘坐；若当前到站列车为小交路列车，部分跨交路乘客选择乘坐，其须在小交路折返站F下车并换乘后续大交路列车，其余跨交路乘客选择乘坐后续大交路列车。令车站i目的地为j的跨交路乘客选择乘坐小交路列车比例为pi,j{i∈Zs(≠F),j∈Zn} ，其余(1 -pi,j)比例乘客选择乘坐后续大交路列车。

第3 类：起讫点均在大交路非共线车站{O∈(Zn∪F),D∈Zn} 的乘客，只能乘坐大交路列车。

基于上述3 种客流类型，车次k在车站i上车乘客数及车次k在车站i下车乘客数需根据列车类型及所服务车站分别进行计算。在客流饱和情况下，由于列车载客量限制，站台仅有一部分乘客能够登乘当前列车，其他乘客需等待下一次列车。

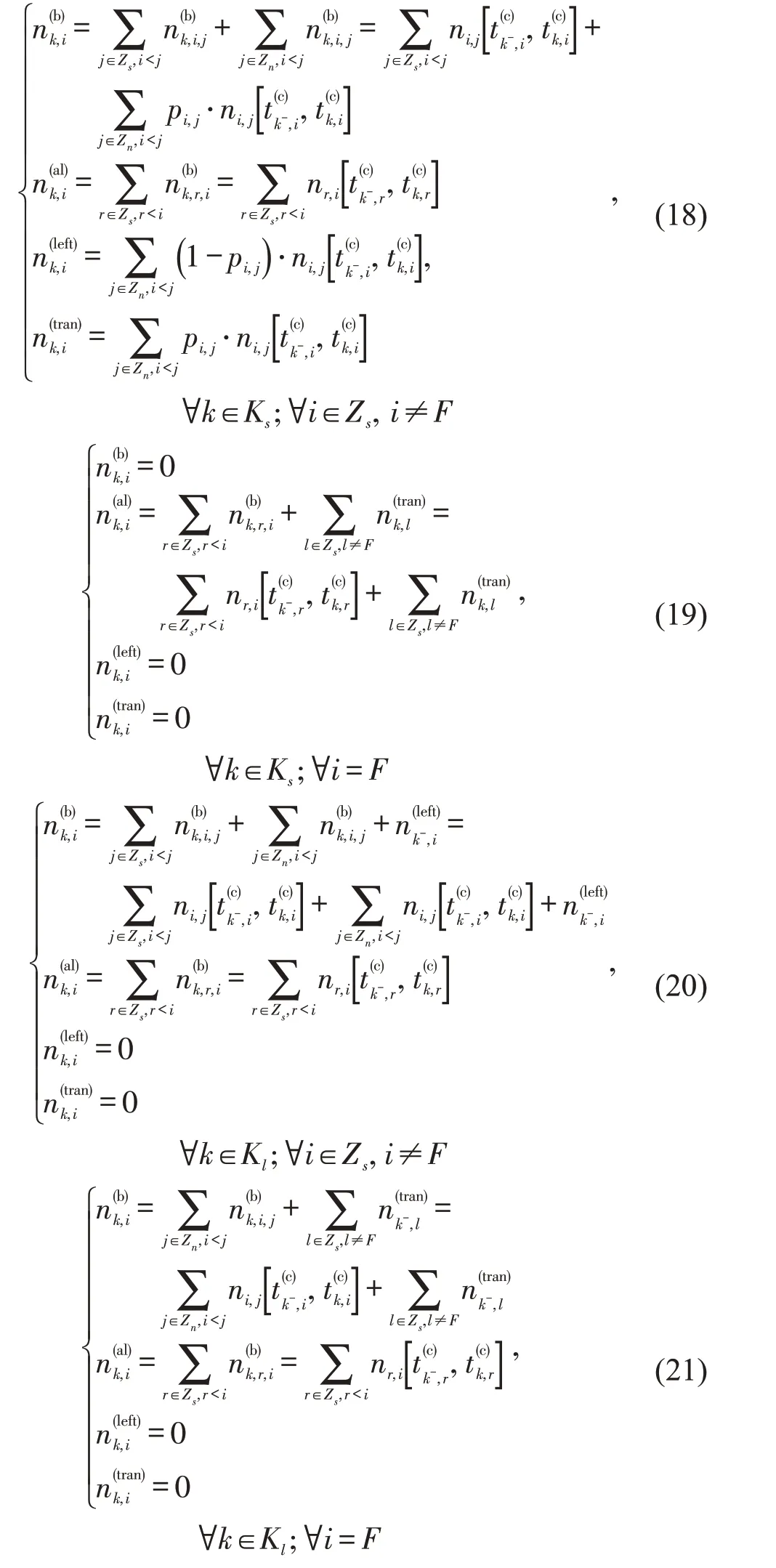
ni,j[] 计算式为

式中：τi,j(t)为t时刻以车站i为起点、车站j为终点的乘客到达率。

式中：lk(t)为车次k在t时刻的载客量，t∈T；δmax为列车最大载客系数；ck为列车额定载客量；为[t,t+1]时间段内车站i分配到车次k的到站乘客数。

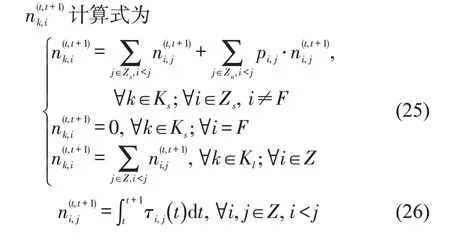
车次k驶离车站i时，滞留站台乘客数为

列车最大负载率约束为

式中：δk,i为列车k在区间[i,i+1]的负载率。

2.3 目标函数

协同优化目标为乘客平均旅行时间与列车发车间隔平均偏离值。目标函数为

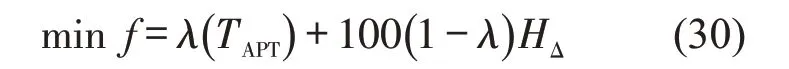
式中：λ为权重系数；TAPT为乘客平均旅行时间；HΔ为列车发车间隔平均偏离值。

乘客平均旅行时间由乘客平均等待时间TAWT及乘客随车平均旅行时间TATT组成，即

式中：TWT为乘客总等待时间；TTT为乘客随车总旅行时间；Ntotal为研究时段内列车总载客数。

乘客总等待时间TWT由登程当前列车乘客的等待时间TWT1及滞留站台乘客的等待时间TWT2组成，即

TWT1及TWT2分别为

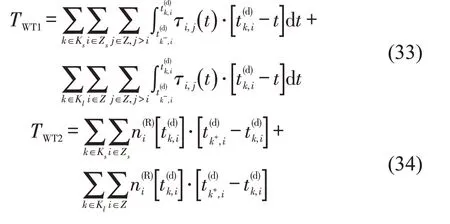
乘客随车总旅行时间及列车总载客数分别为

列车发车间隔平均偏离值HΔ为

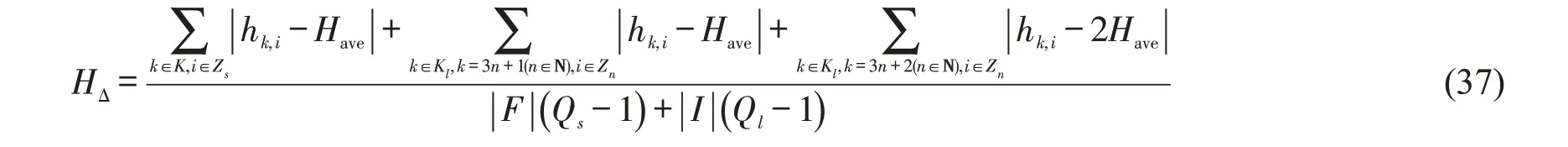
式中：|F|、|I|分别为站台F、站台I对应的编号值。

2.4 模型求解

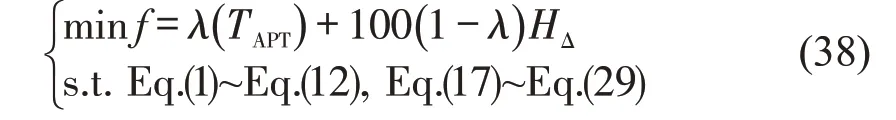
本文所构建高峰时段基于非均匀发车间隔的大小交路时刻表优化模型为利用计算机仿真程序将客流量按照列车时刻表加载至每一列计划列车，并通过模拟退火算法进行迭代，不断逼近目标函数最小值，实现客流需求与列车运行计划的耦合。

3 案例分析

该模型本质为大规模组合优化问题，模拟退火算法是求解大规模组合问题的有效算法，能够在理想时间内求得满意解。本文设计模拟退火启发式算法求解模型，每一组解对应一组列车时刻表。将目前高峰时段列车开行方案及时刻表作为初始解，

3.1 基础数据及参数

某城市轨道交通线路全长41.57 km，共设23座车站。上、下行共设置46个站台，站台16为小交路折返站台。运营列车为6节编组B型车。早高峰时段为7:30-9:00。全线各区段客流量不均衡程度大，开行比例为2∶1(ε=2)的大、小交路。列车及模型相关参数设置如表1所示。

表1 相关参数设置Table 1 Parameter setting

本线路客流在空间分布上呈现明显的潮汐现象。第7、8、9站为全线客流量最为集中的车站，早高峰时段大量通勤乘客从居住地前往市中心区，导致下行方向断面客流从第1 站到第9 站不断增加，从第10站开始逐渐减小。高峰时段全线大部分车站存在客流量最大的峰值时刻点，第7、8、9站峰值时刻点分别为8:22、8:29、8:27。峰值点之前客流量随时间增加而递增，峰值时间点之后客流量随时间增加而递减。如图2所示，优化前开行等间隔列车情况下，08:35-08:40期间第7、8、9站站台滞留乘客分别达到284，295，227 人；列车在第7、8、9 站最大满载率均为1.2，处于最大载客量状态，乘客须滞留站台等待下一趟列车。

图2 优化前站台未上车乘客数Fig.2 Number of passengers not getting on train under current timetable

3.2 结果分析

在Inter(R) Core(TM) i3-9100 CPU 3.60 GHz 处理器、8.00 GB 内存、Windows10 64 位操作系统个人计算机上，采用Matlab R2019b 编程。在初始温度为600，终止温度为1，温度衰减系数0.9，马尔科夫链长度为1000 的设置下，目标函数取得最小值minf=λ(TAPT)+100(1 -λ)HΔ=1075.72 s。此时乘客平均旅行时间TAPT为886.2 s(比优化前减少45.3 s，优化比例为4.9%)，其中，乘客平均等待时间TAWT为71.1 s，乘客随车平均旅行时间TATT为815.1 s(每个站平均停站时间减少1.2 s，每个区间运行时间平均减少3.7 s)。列车发车间隔平均偏离值HΔ为13.6 s。

图3 为优化后高峰时段下行方向列车从首站到第9站的局部运行线。从图中可以看出，早高峰时段7:30-9:00 共开行46 次列车(平均发车间隔为120 s)。早高峰中间时段列车开行间隔较小，早高峰初期及后期列车开行间隔较大。具体地，从图4(优化前后列车在首站的发车间隔)及表2(优化后列车首站发车时刻表)可知，优化前后早高峰时段均发出46 次列车。优化前开行120 s 等间隔列车。优化后，7:30:00-7:53:49 共发出12 次列车，发车间隔由152 s 逐渐加密至110 s，平均发车间隔为130 s；7:53:50-8:31:37 共发出21 次列车，发车间隔均为108 s；8:31:38-9:00:00 时段共发出13 列列车，发车间隔由109 s逐渐加密至161 s，平均发车间隔为131 s。

表2 优化后列车首站发车时刻表Table 2 Train departure time at departure station under optimized timetable

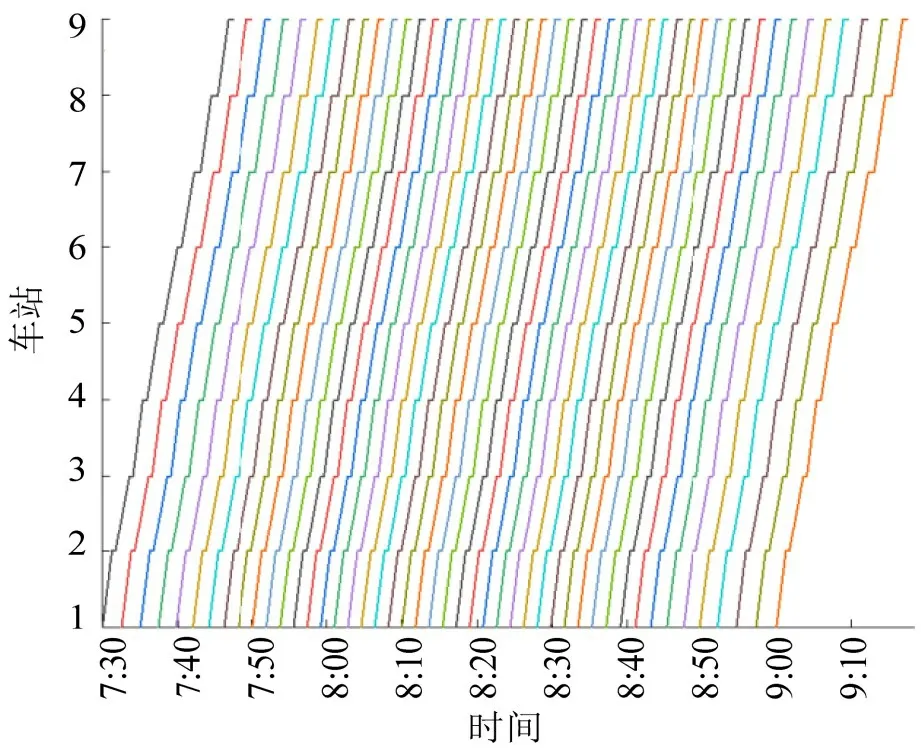
图3 优化后局部运行线(下行方向从首站到第9站)Fig.3 Part of optimized train timetable(running from station 1 to station 9 of down direction)

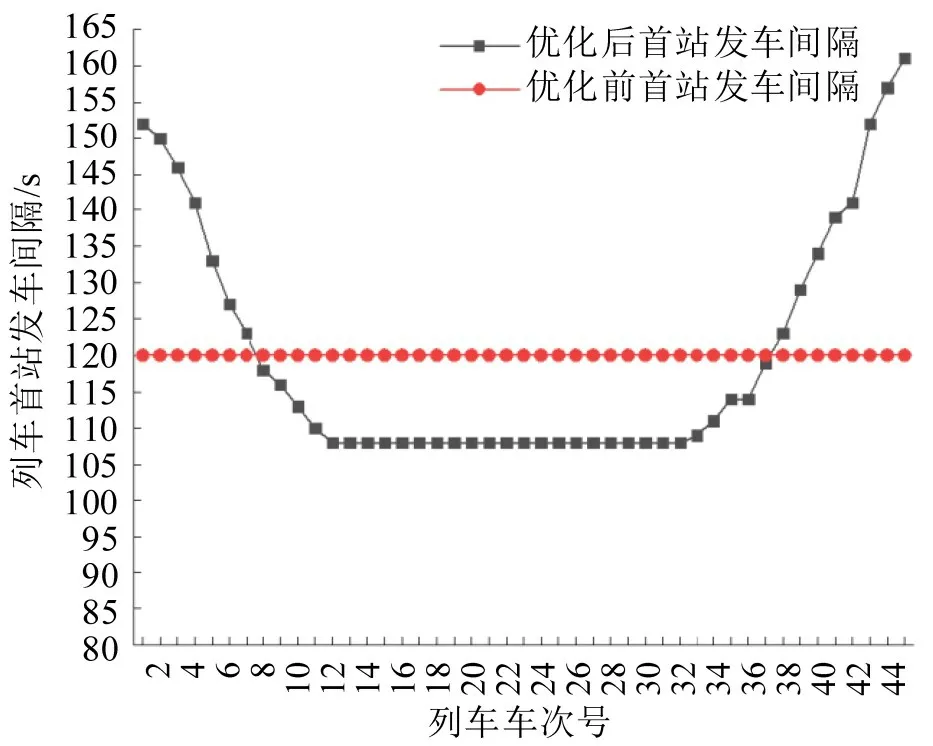
图4 优化前后列车在首站的发车间隔Fig.4 Train departure interval at station 1 under optimized and current timetables

列车从首站发出后，经过约12，14，17 min分别到达第7、8、9站。由此可推算出：优化后上述时间段(7:53:50-8:31:37)从首站发出的高频次列车可有效服务于第7、8、9 站高峰客流。得益于优化时刻表增大了车站客流高峰时段发车频率，优化后高峰时段所有乘客均能登乘当前列车，站台均无滞留乘客。从图5可知：优化后列车在各个车站的最大满载率较优化前均有所降低，降低幅度为1.8%～8.5%。列车在第7、8、9 站最大满载率分别降低至1.109、1.098、1.102，优化幅度分别为7.6%、8.5%、8.2%；优化后乘客在各个车站的平均等待时间均有所减少，减少幅度为0.4%～13.1%。减少幅度最大的为第7、8、9站，分别为11.7%、13.1%、11.9%。

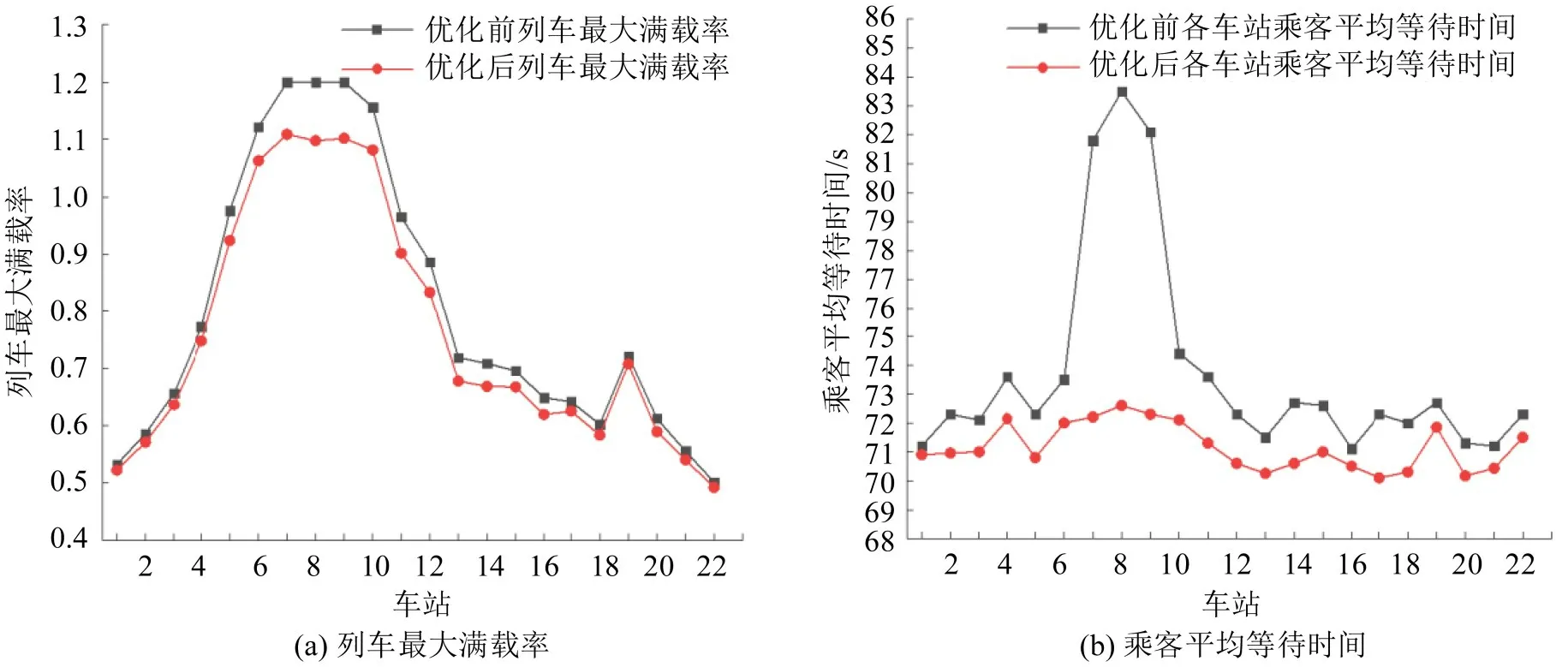
图5 优化前后各车站列车最大满载率及乘客平均等待时间Fig.5 Maximum train loading rate and average waiting times of passengers under optimized and current timetables

由表3可知，优化后列车在各车站的平均停站时间除第7、8 站外均有所减少，优化比例为1.8%～7.3%。列车在第7、8 站停站时间较优化前略有增加，这是因为第7、8 站为客流量较大的换乘车站，既有停站时间不能满足上、下车客流需求，故优化后增加了停站时间以精确匹配上、下车客流量。优化后，列车在各个车站总停站时间较优化前减少了26 s，对减少乘客旅行时间具有一定的优化效果。

表3 优化前后列车平均停站时间Table 3 Average train dwell times under optimized and current timetables

由上述数据及分析可知，优化后的运行线在不增加列车开行次数的前提下，增大了车站高峰时段发车频率并实现了运力的精准投放，对乘客旅行时间、乘客等待时间及列车负载率等起到了较好的优化效果。

3.3 灵敏度分析

(1)目标函数权重系数λ对模型的影响

设置不同权重系数λ，分析其对模型的影响，结果如图6所示。λ从0.0逐渐增至1.0的过程中，乘客平均旅行时间不断减小，列车发车间隔平均偏离值不断增大，体现了目标函数对乘客平均旅行时间及列车发车间隔平均偏离值的协同优化。值得一提的是，λ从0.6 增至1.0 的过程中，乘客平均旅行时间降幅明显变缓，且列车发车间隔平均偏离值较大(λ=0.7 时达到19.6 s)，故3.2节中λ取值为0.6。

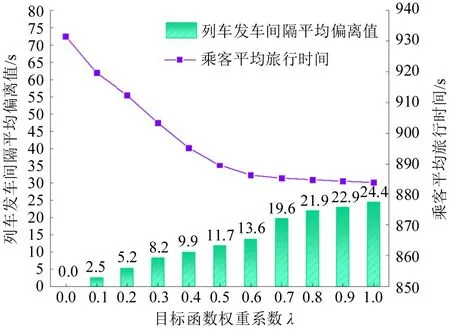
图6 不同目标函数权重系数下乘客平均旅行时间及列车发车间隔平均偏离值Fig.6 Average travel times of passengers and deviation values of train departure interval under different weights

图7 展示了不同权重系数下各车站乘客平均等待时间。当λ从0.0逐渐增大到1.0，各车站乘客平均等待时间均不断减小，结果与预期相符。特别地，当λ=0.0 时，所对应时刻表为等间隔时刻表。

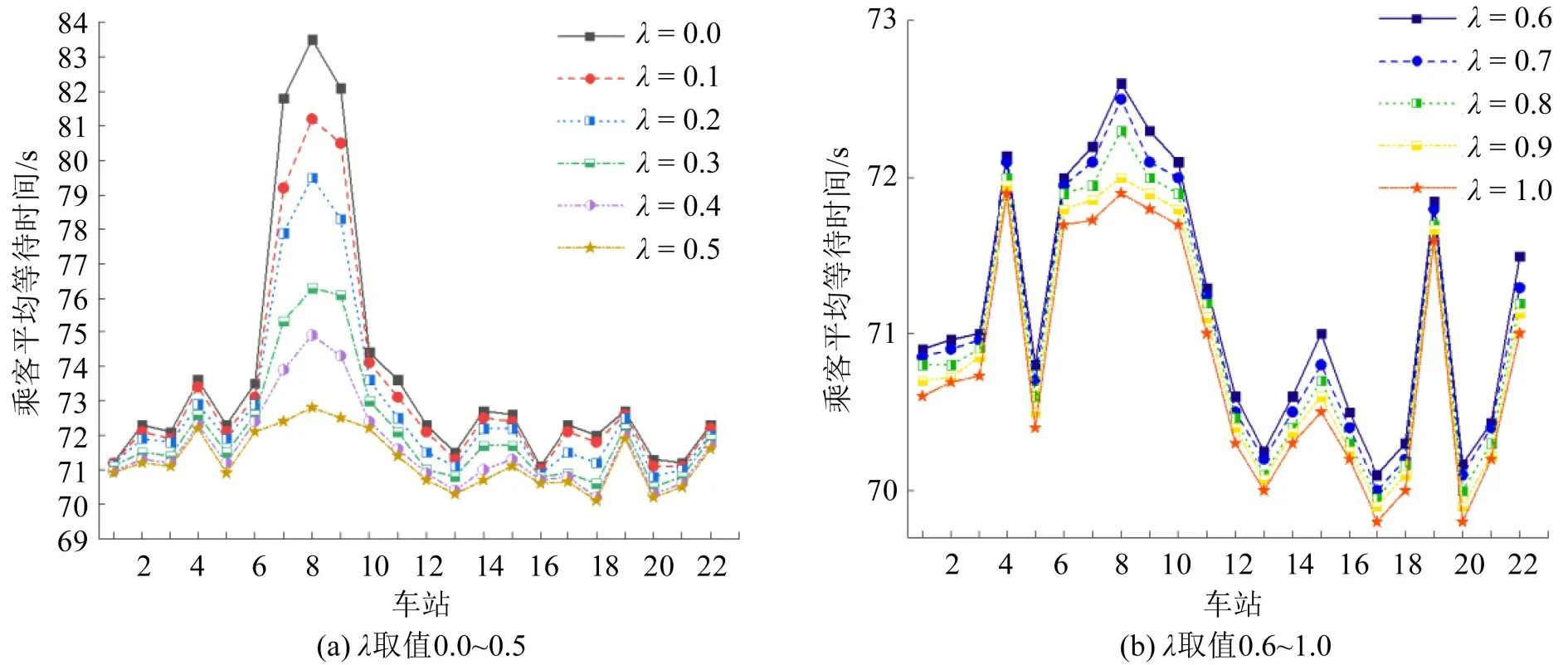
图7 不同目标函数权重系数下各车站乘客平均等待时间(λ=0.0～1.0)Fig.7 Average waiting times of passengers at each station under different weights (λ=0.0～1.0)

图8 展示了不同权重系数下各车站发车间隔平均偏离值。当λ从0.1逐渐增大到1.0，各车站发车间隔平均偏离值均不断增大，结果与预期相符。当λ=0.0 时，发车间隔平均偏离值为0。

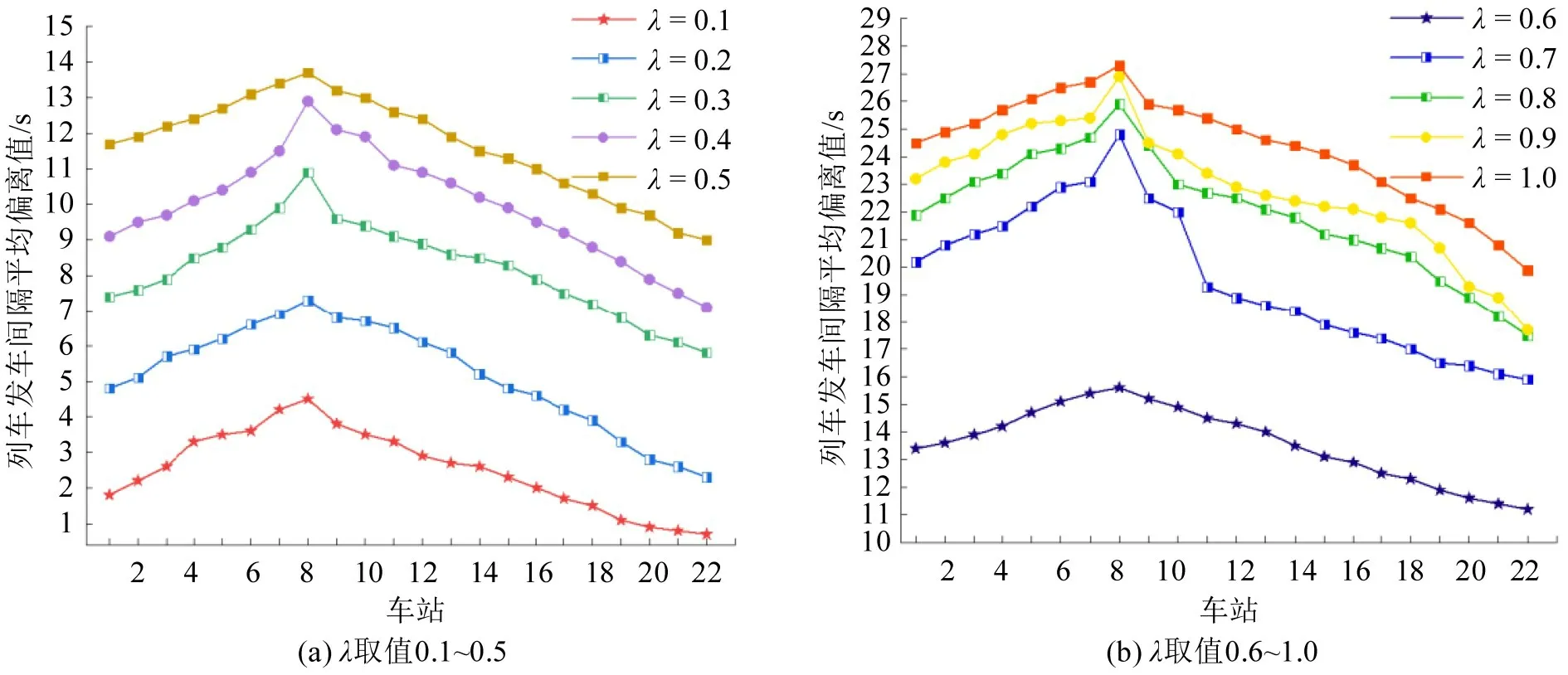
图8 不同目标函数权重系数下各车站列车发车间隔平均偏离值(λ=0.1～1.0)Fig.8 Average deviation values of train departure interval at each station under different weights (λ=0.1～1.0)

(2)平均发车间隔Have对模型的影响

平均发车间隔对模型相关输出的影响如表4所示。由表4 可知：随着列车平均发车间隔由120 s 逐渐加密至111 s，优化后投入车次数由46次增至49 次，运力不断加大；列车最大满载率、发车间隔平均偏离值及乘客平均旅行时间均不断减少。

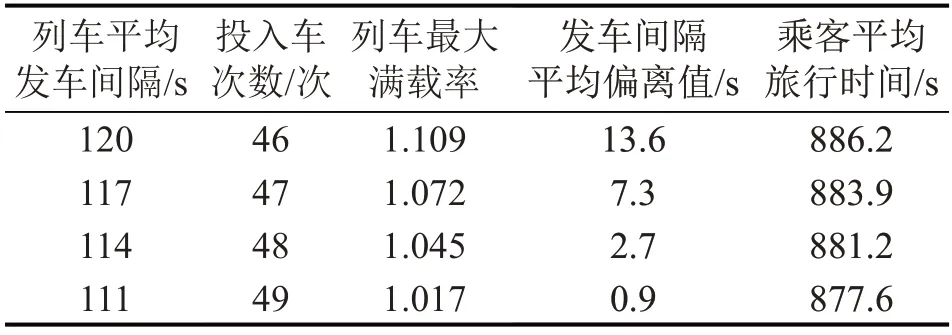
表4 平均发车间隔对模型相关输出的影响Table 4 Influence of average departure interval on related model outputs

以上灵敏度分析表明，本模型具有良好的可用性及稳定性。

4 结论

本文建立了高峰时段基于非均匀发车间隔的大小交路列车时刻表优化模型，对乘客平均旅行时间及列车发车间隔平均偏离值进行协同优化。优化后乘客平均旅行时间比优化前减少45.3 s，优化比例为4.9%；列车发车间隔平均偏离值为13.6 s。案例分析结果表明：

(1)优化后列车运力与客流需求更加匹配，有效降低了乘客平均等待时间。乘客在各个车站的平均等待时间减少幅度为0.4%～13.1%，减少幅度最大的为第7、8、9站，分别为11.7%、13.1%、11.9%。

(2)优化后有效降低了站台滞留乘客数及列车最大满载率。优化后所有车站站台均无滞留乘客，体现了列车运输能力较好地匹配了客流需求；列车在各个车站的最大满载率较优化前均有所降低，降低幅度为1.8%～8.5%。第7、8、9站最大满载率由优化前均为1.2 分别降低为1.109、1.098、1.102，从而可降低安全风险，减轻运营部门压力。

(3)相较于既有等间隔时刻表列车在车站停站时间为一固定值，优化模型中将列车在各个车站的停站时间与其上、下车乘客数量相关联。优化后，除全线客流量较大的第7、8站外，列车在其他车站的停站时间均有所减少，减少幅度为1.8%～7.3%，对优化乘客旅行时间有一定的作用。

(4)灵敏度分析讨论了目标函数权重系数及平均发车间隔对模型的影响，证明本文模型具有良好的可用性及稳定性，能够为城市轨道交通时刻表优化提供参考。