考虑多时间尺度特征的城市轨道交通短时客流量预测模型

张文娟，杨皓哲，张彬，李秀杰

(同济大学，机械与能源工程学院，上海 201804)

0 引言

近年来，智能交通系统已经成为增强交通系统性能、提高乘客出行安全以及为乘客提供更多出行选择的有力支撑[1]。随着我国智能交通系统和大数据技术的发展，城市轨道交通AFC 系统积累了海量蕴藏客流变化规律的原始数据，通过智能算法等方法对其进行深度挖掘，可以准确预测未来客流量，有助于车站的组织运营与应急响应，具有重要的现实意义和研究价值。

长期以来，数理统计模型广泛应用于城市轨道交通客流预测问题，经典的统计方法包括自回归积分移动平均(Autoregressive Integrated Moving Average,ARIMA)模型、逻辑回归模型及卡尔曼滤波器等。例如，赵鹏等[2]在分析客流变化规律的基础上，构建季节ARIMA 模型预测出站客流。JIAO等[3]提出3种基于修正的卡尔曼滤波器的客流预测模型，并证明了3种模型预测效果的准确性与稳定性。

随着交通大数据的发展与应用，基于机器学习模型的城市轨道交通客流预测研究取得了丰硕成果。机器学习方法包括贝叶斯网络、K最近邻算法(K-Nearest-Neighbor, KNN)、支持向量回归及神经网络等，例如，郇宁等[4]提出一种改进模式匹配方法的KNN算法，用于客流量滚动实时预测。LI等[5]提出一种新的动态径向基函数神经网络用于出站客流预测，该网络创新性地集成了进出站客流量、列车时刻表与客流控制系数。相较于传统的线性模型，机器学习模型通过分析和挖掘大量历史数据，能够较好地应对客流变化的随机性和非线性规律，具有较为显著的优势。

作为机器学习的分支，深度学习模型基于层次更深和结构更复杂的神经网络，能够较为准确地拟合输入与输出数据之间的强非线性关系。近年来，得益于海量的交通数据和高性能计算技术，基于深度学习的城市轨道交通客流预测研究成果颇多。例如，LIU 等[6]提出一种基于长短期记忆(Long-Short Term Memory,LSTM)神经网络的客流预测模型，称为DeepPF，该模型具有高度的灵活性和可扩展性。YANG等[7]提出一种将小波分析和LSTM神经网络结合的进站客流预测模型，将进站客流通过小波分析分解后输入LSTM 神经网络。许多研究融合了两种及以上单一深度学习模型，结合不同模型各自的优势，提高预测精度。例如，ZHANG 等[8]提出一种融合残差网络、图卷积网络与LSTM的混合模型，称为ResLSTM，实现了城市轨道交通全网规模进出站客流预测。赵建立等[9]构建一种基于卷积神经网络和残差网络的混合模型，用于多站点进出站客流预测。

Transformer是一种新兴的深度学习模型[10]，自2017 年在自然语言处理领域提出以来获得了广泛关注，该模型采用完全基于注意力机制的特殊结构，解决了循环神经网络无法对信息并行计算和缺乏对序列数据周期性建模等缺陷。目前，有学者将其引入客流预测中，并取得了突出表现。例如，LIN等[11]构建基于Transformer 的城市轨道交通客流预测模型，并与包括回归模型、Boosting 模型及深度学习模型等在内的10 个基线模型进行对比，结果表明，基于Transformer的模型拥有最佳的预测性能。

上述研究对城市轨道交通短时客流预测均有重要的参考价值，但也存在一定的改进空间。大部分模型没有考虑客流变化的周期性规律，导致时间特征挖掘不够充分，从而影响预测精度。另外，一些模型虽然能够满足预测的准确率要求，但是，由于模型复杂度过高，导致计算效率较低，且难以满足较小时间粒度预测的实际需求，忽略了模型的高效性和实用性。针对上述问题，本文提出一种结合GRU 神经网络和Transformer 的混合深度学习模型，利用两者处理序列数据的独特优势，充分挖掘长时间跨度客流数据的连续依赖性和周期依赖性。此外，模型采用子模块并联的网络结构，具有较高的计算效率，适用于城市轨道交通各类型车站，具备较好的普适性。

1 问题描述与特征建模

1.1问题描述

本文重点研究城市轨道交通单个车站的短时客流量预测问题，利用AFC 系统历史刷卡数据来同时预测站点未来的进站量与出站量，即对于预测目标时间步t，将过去连续T个时间步的客流数据输入预测模型，预测下一时间步客流量。Xt=()T∈ℝ2为t时间步真实客流量，其中，,分别为真实进站量与出站量。Yt=()T∈ℝ2表示t时间步预测客流量，其中，,分别为预测进站量与出站量。综上，本文界定的城市轨道交通客流量预测问题为

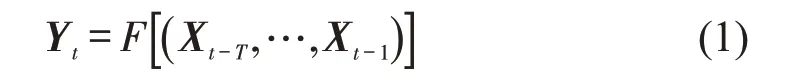
式中：F(·) 为映射函数；(Xt-T,…,Xt-1) ∈ℝ2×T为历史客流矩阵。

1.2 多时间尺度特征建模

为了充分挖掘客流时间序列数据中隐含的连续性和周期性信息，本文对历史客流数据的周周期依赖性、日周期依赖性以及相邻时段依赖性这3种时间特性分别进行建模。假设将每日总时长等间隔划分为k个时间步，对于某预测目标时间步t，以3 种时间尺度分别沿时间轴截取时间片段Pweek，Pday，Pnear，并分别用变量w、d、n表示各时间片段所包含时间步的数量大小。Xweek，Xday，Xnear为各时间片段所对应的历史客流量矩阵，将作为模型的各个输入分量。为更好地展示建模过程，现假设t代表2021年7月15日(周四)8:00-8:05，客流特征矩阵建模过程如下。

(1)周周期时间片段客流矩阵Xweek

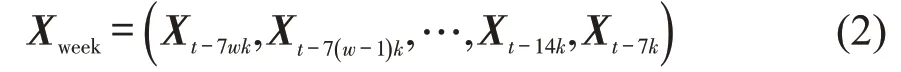
如式(2)所示，该周期下客流量矩阵由时间步t的前w周每周同一时间步客流量组成，例如，当w=2 时，其对应时间片段Pweek在时间轴上的位置如图1所示。

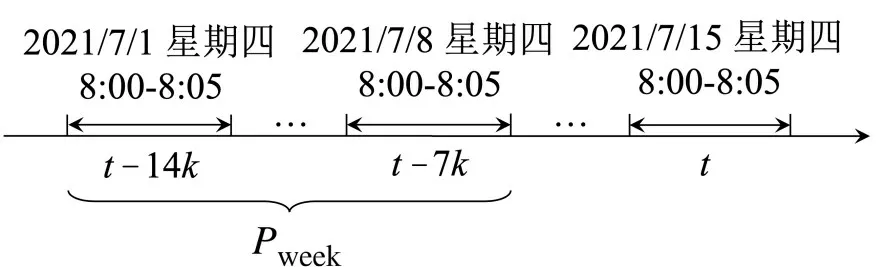
图1 周周期时间片段Fig.1 Weekly periodic time segment

(2)日周期时间片段客流Xday

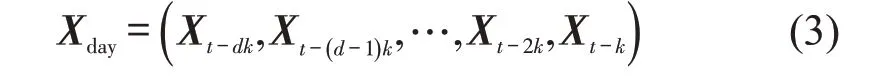
如式(3)所示，该周期下客流量矩阵由时间步t的前d天每天同一时间步客流量组成，例如，当d=2 时，其对应的时间片段Pday在时间轴上的位置如图2所示。

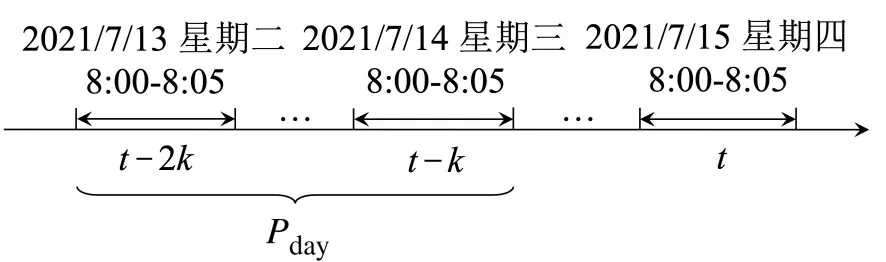
图2 日周期时间片段Fig.2 Daily periodic time segment

(3)相邻时间片段客流Xnear

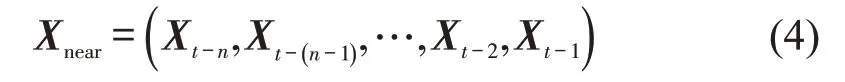
如式(4)所示，该周期下客流量矩阵由时间步t之前的连续n个时间步客流量组成，例如，当n=6时，其对应的时间片段Pnear在时间轴上的位置如图3所示。

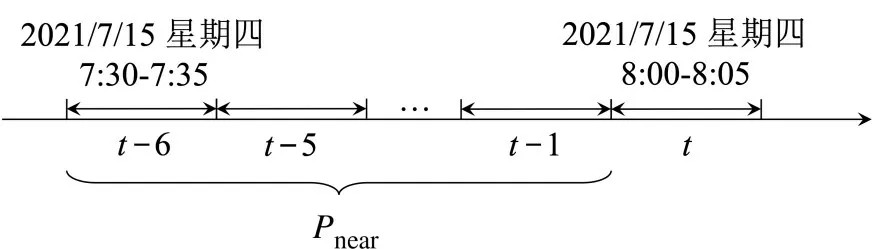
图3 相邻时间片段Fig.3 Recent time segment

综上所述，对于预测目标时间步t，将Xweek，Xday，Xnear这3个矩阵进行合并，得到最终的模型输入客流矩阵Xpast=(Xweek,Xday,Xnear)∈ℝ2×(w+d+n)。用Xpast代替式(1)中的历史客流矩阵(Xt-T,…,Xt-1) ，则式(1)转化为

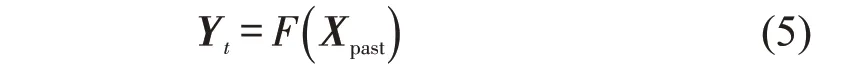
2 混合深度学习模型构建

本文提出一种融合多时间尺度时序特征的混合深度学习模型，即GRU-Transformer模型，该模型主要包含两个模块：(1)Attention-GRU 模块，该模块将GRU 与Attention 机制结合；(2) Conv-Transformer模块，该模块由多层以一维卷积神经网络(CNN1D)改进的Transformer 编码层组成。具体结构如图4所示。

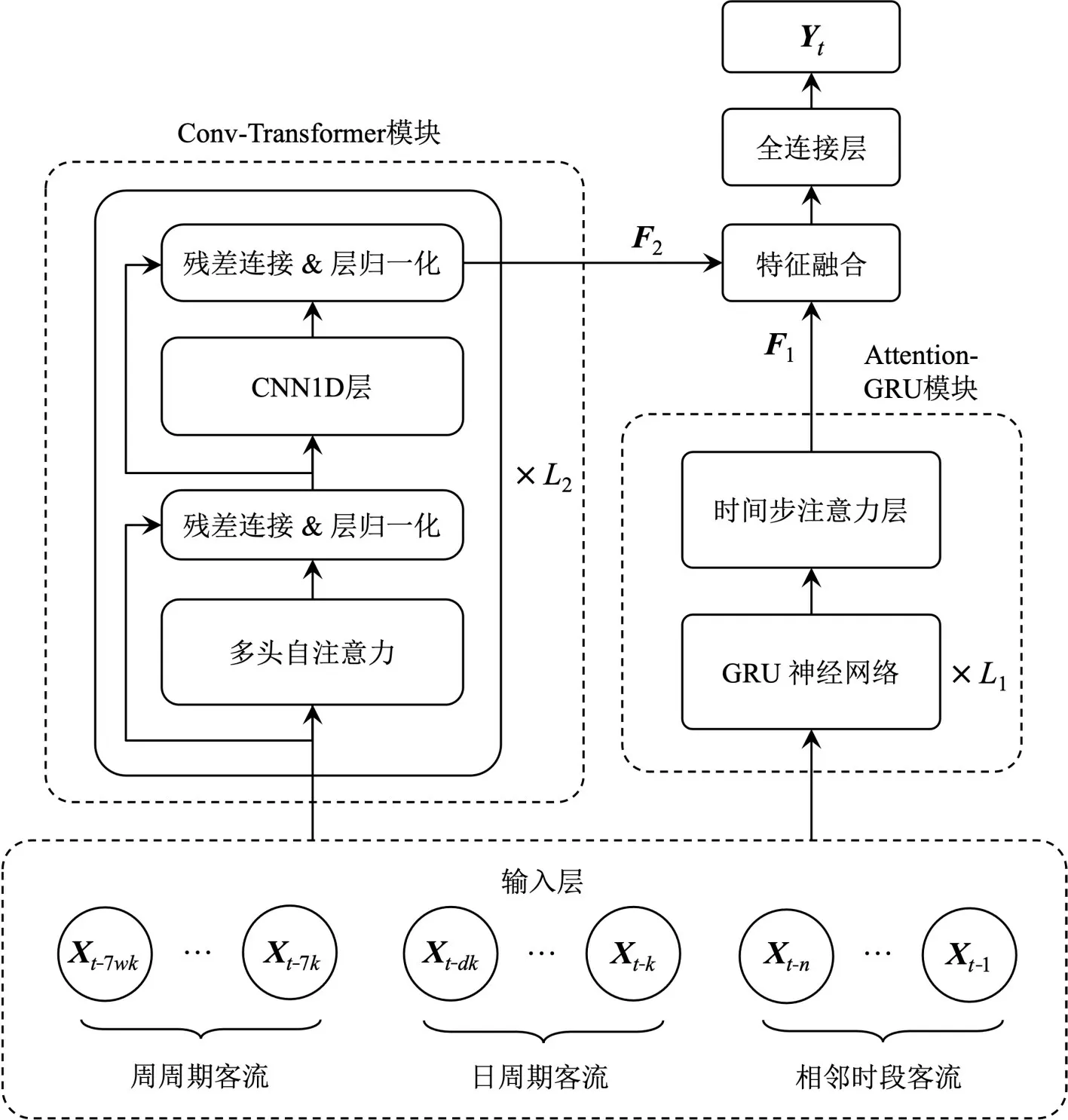
图4 GRU-Transformer模型结构Fig.4 Framework of GRU-Transformer model

2.1 Attention-GRU模块

针对RNN 无法处理长序列依赖关系的缺陷，Hochreiter 等[12]提出了LSTM 神经网络，通过输入门、输出门和遗忘门对序列数据进行长期记忆，有效解决了RNN容易出现的梯度消失和梯度爆炸问题，然而LSTM 单元内部结构较为复杂，导致模型训练需要花费很长时间。Cho 等[13]于2014 年提出了LSTM的变体GRU，其结构相较于LSTM更为简单，需要训练的参数更少且能够保持与LSTM相近的预测效果，因此，本文使用GRU神经网络学习客流的连续性特征，其单元结构如图5所示。

GRU 单元通过重置门rm和更新门zm对客流信息进行读取、记忆和参数更新。如图5 所示，xm为m时间步的输入客流量，hm-1为m-1 时间步GRU 单元输出的隐藏层状态向量，即上一GRU 单元学习并传递下来的客流特征信息。xm和hm-1输入当前GRU 单元后，通过计算获取重置门rm和更新门zm两个门控状态，rm用来控制舍弃与保留前一时间步客流状态信息的程度；zm用来控制前一时间步客流状态信息保存到当前状态中的量，zm的值越大，说明当前时间步客流状态信息保留得越多，前一时间步客流状态信息保留得越少。GRU单元最终输出当前隐藏层状态向量hm，并传递至下一时间步。计算式归纳为

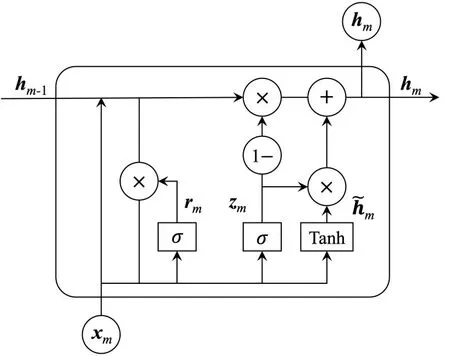
图5 GRU单元结构Fig.5 GRU unit structure

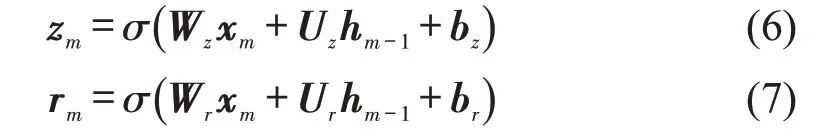
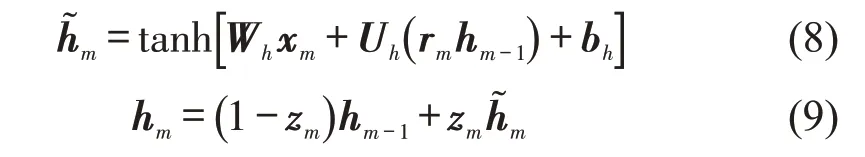
式中：σ(·)为sigmoid 激活函数，其输出范围为[0,1]；h͂m为候选隐藏状态；tanh(·)为双曲线正切激活函数；Wz,Wr,Wh,Uz,Ur,Uh为权重矩阵；bz,br,bh为偏置项。

Attention-GRU模块中GRU网络层数为L1，每一层GRU 网络均由一系列结构相同的GRU 单元串联组成。GRU 单元隐藏神经元数量均设置为32，每一层GRU 层所包含GRU 单元个数均与Xpast列数(w+d+n)相等，因此，GRU 网络的输出为32×(w+d+n)矩阵，该矩阵表示GRU 网络学习客流连续性特征的结果。

为了拟合各时间步客流量对模型预测影响程度的大小并提升预测精度，本文采用注意力机制为GRU网络输出的每一步隐藏层状态分配注意力权重。模型首先计算每个时间步输出隐藏层状态的注意力权重大小，然后，进行Softmax归一化将各注意力权重均缩放至[0,1]，得到每个时间步注意力得分，注意力得分值越大表示该时间步客流量对模型预测的贡献度越大。最后，将各注意力得分与对应的GRU 层输出隐藏层信息进行加权求和，输出客流连续性特征F1。由于时间步注意力层仅进行权重分配而不改变输入矩阵尺寸大小，因此，F1仍为32×(w+d+n)矩阵，计算式归纳为

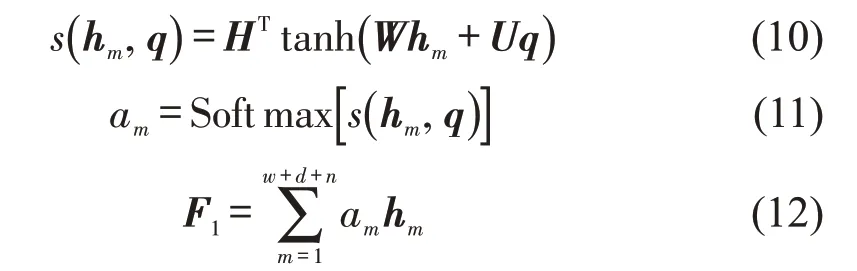
式中：m=1,2,…,(w+d+n)；q为查询向量；s(hm,q)为第m步客流量的注意力权重，表示hm与q的相似程度；H,W,U为训练参数；am为第m个时间步的注意力得分。

2.2 Conv-Transformer模块

Transformer模型的核心是多头自注意力机制，其采用位置编码的方式获取输入序列的位置信息，用于捕捉输入序列位置关系。由于客流预测中输入数据与输出数据在时间轴上是连续的，两者不存在语义模型中的位置对应关系，因此原始Transformer 模型的位置编码方法不适用于客流预测。针对此问题，本文不采用位置编码操作，而是将前文介绍的Attention-GRU 模块与Transformer并联，以弥补Transformer 在拟合数据连续性方面的缺陷。同时，本文采用Transformer 原始模型中编码器部分，利用多头自注意力机制和CNN1D 充分挖掘客流数据的周期性特征。

2.2.1 多头自注意力机制

自注意力机制是一种缩放点积注意力(Scaled dot-product Attention)，通过查询向量(Q)与键向量(K)-值向量(V)对之间的交互实现信息的动态聚合[14]。本文中，自注意力机制通过Q、K和V计算输入客流矩阵Xpast中每个时间步客流量与其余时间步客流量之间的相关性，即拟合客流周期性特征。具体计算步骤如下。

Step 1 输入客流矩阵Xpast分别与尺寸大小相同的3个权重矩阵WQ、WK、WV进行矩阵相乘操作得到Q、K、V矩阵，三者均为Xpast的线性变换，因此，均可作为Xpast的代表矩阵用于计算Xpast对自身的注意力权重，其计算过程示意图如图6所示。

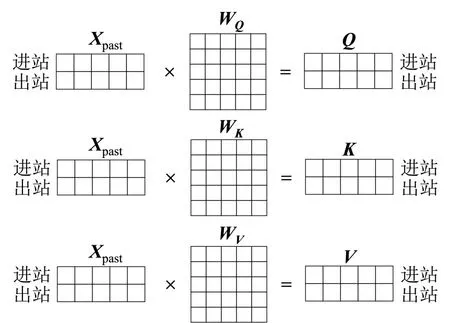
图6 自注意力机制Fig.6 Self attention mechanism

Step 2 将Q转置后与K进行矩阵相乘，计算Q中每一时间步与其余各时间步(即K中每一个列向量)客流向量之间的相似度。然后，将所得矩阵各值除以客流向量维度l的1/2次方进行缩放。最后，进行Softmax函数处理将权值归一化，得到Q、K之间的相似度矩阵S∈ℝ(w+d+n)×(w+d+n)。如图7 所示，S中第u(u=1,2,…,(w+d+n))行表示第u个时间步客流量与其余各时间步(包括自身)客流量的关联度大小，各权值均为正数，且和为1。

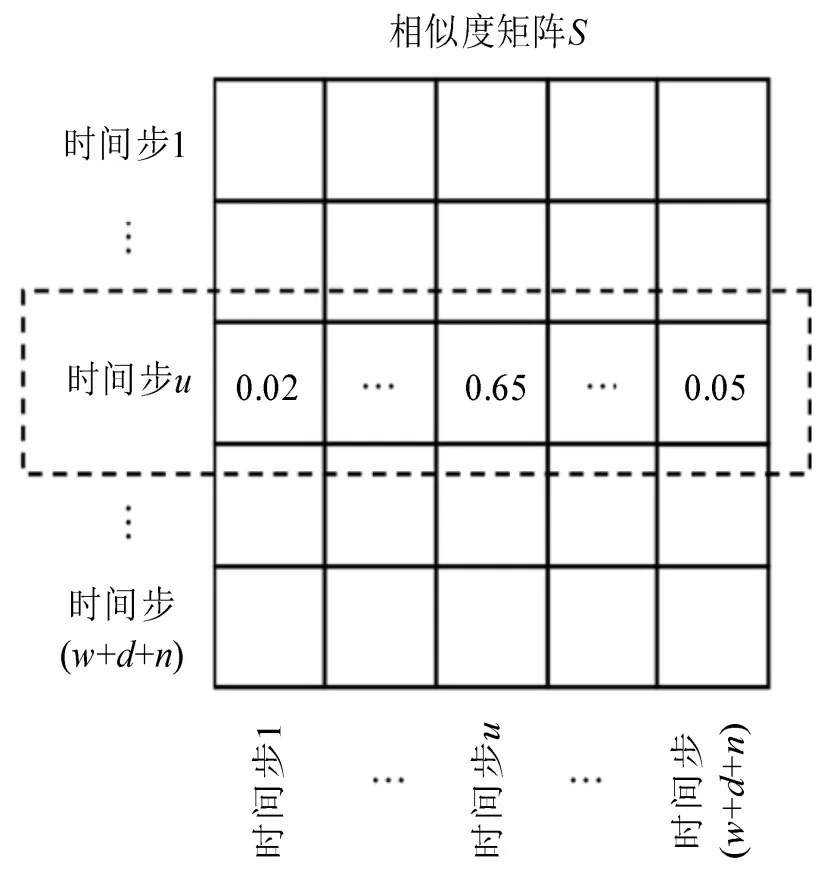
图7 相似度矩阵Fig.7 Similarity matrix

Step 3 将V与ST进行矩阵相乘，得到自注意力机制输出Z(Xpast)∈ℝ2×(w+d+n)。相较于Xpast，Z(Xpast)中每一时间步客流信息都通过加权和的方式融合了其余各个时间步客流信息，即拟合了各时间步之间的周期关联性。自注意力机制计算公式归纳为

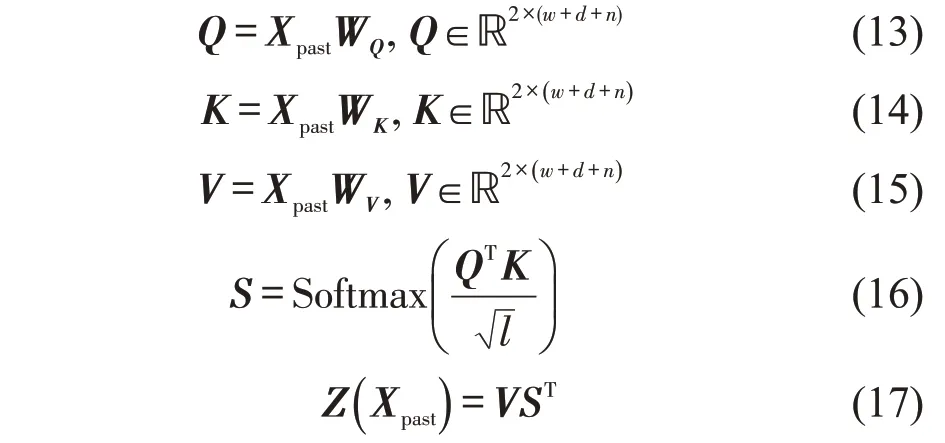
为使模型在不同的表示子空间里学习相关信息[15]，从而充分挖掘客流周期性特征，本文采用多头自注意力机制，其过程如图8 所示。本文设置p个自注意力头并行计算，然后，将每个自注意力头的输出横向拼接，得到一个2×[(w+d+n)×p] 矩阵，将其与映射矩阵WO∈ℝ[(w+d+n)×p]×(w+d+n)相乘得到多头自注意力机制输出ZM(Xpast)∈ℝ2×(w+d+n)。WO的作用是将所有客流周期性信息进行聚合，并将输出转换为与输入矩阵尺寸大小相同的2×(w+d+n)矩阵，使得ZM(Xpast)融合了所有注意力头的输出信息。计算式为

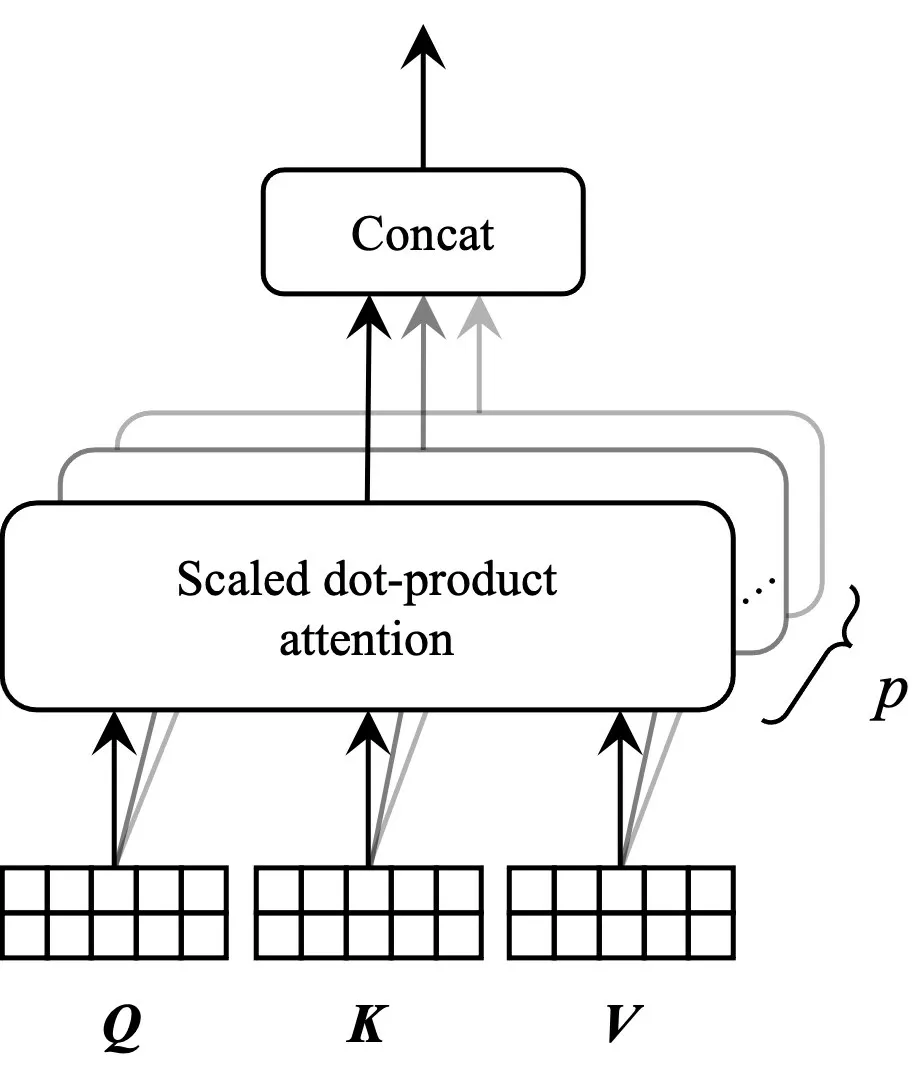
图8 多头自注意力机制Fig.8 Multi-head self-attention mechanism

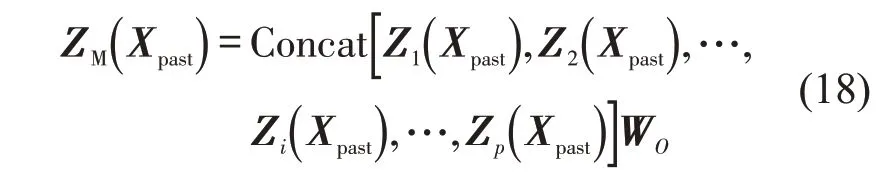
式中：Concat(·) 为矩阵拼接函数；Zi(Xpast)为第i个自注意力头的输出。

2.2.2 Conv-Transformer层

CNN1D 常用于处理文本与时间序列数据，本文将原始Transformer 模型中的前馈层改进为CNN1D，加强Transformer 对时间序列信息的挖掘能力。为保证计算过程中每一个子层的输入与输出矩阵尺寸大小均相同，CNN1D 层输入Xc应为2×(w+d+n)矩阵。由于Xc的行数为2，因此，将卷积核大小设为2×2，同时将卷积核滑动步长设为1。CNN1D层操作如图9 所示，其计算步骤如下。

图9 CNN1D处理序列数据示意图Fig.9 Schematic diagram of CNN1D processing sequence data

Step 1 为了使CNN1D 层输出仍为2×(w+d+n)矩阵，对Xc进行same padding操作，即程序自动使用“0”将其填充为2×(w+d+n+1) 矩阵，以避免卷积计算过程中客流矩阵边缘信息的丢失。填充操作如图9中虚线所示。

Step 2 使用2 个卷积核分别沿时间轴与输入矩阵Xc进行卷积操作，得到特征映射C1∈ℝ1×(w+d+n)、C2∈ℝ1×(w+d+n)；

Step 3 将特征映射C1、C2纵向拼接，形成特征图C∈ℝ2×(w+d+n)，即CNN1D层输出。

计算公式归纳为

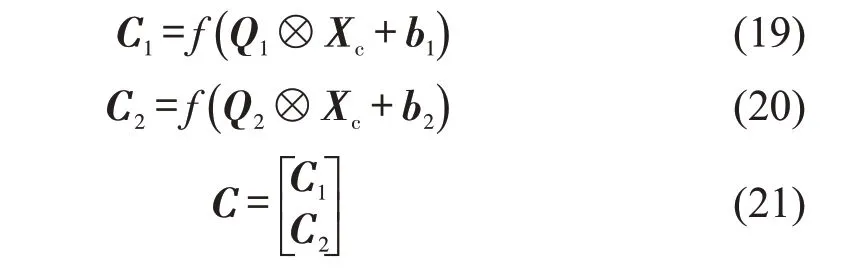
式中：f(·)为激活函数；⊗为卷积运算；Q1、Q2为权重矩阵；b1、b2为偏置项。

将由CNN1D 改进后的Transformer 层称为Conv-Transformer 层，每层由多头注意机制和CNN1D两个子层组成，信息由每一个子层输出后，都将该层输出矩阵与输入矩阵进行残差连接，以避免模型梯度消失、梯度爆炸及网络退化的问题。然后，将所生成的矩阵进行层归一化操作进行数据缩放，进而得到Conv-Transformer层输出。

最终，将L2个结构相同的Conv-Transformer层串联形成Conv-Transformer 模块，其输出结果为客流周期性特征F2∈ℝ2×(w+d+n)。

2.3 特征融合层与全连接层

客流矩阵Xpast同时输入Attention-GRU模块和Conv-Transformer 模块，经两模块分别提取客流连续 性 特 征F1∈ℝ32×(w+d+n)与 客 流 周 期 性 特 征F2∈ℝ2×(w+d+n)。最后经过特征融合层将F1、F2使用矩阵拼接函数进行纵向拼接，得到特征融合信息F∈ℝ34×(w+d+n)。因此，F为模型对客流周期性、连续性特征进行深度挖掘后的结果，可表征预测环节所需全部隐藏信息。特征融合式为

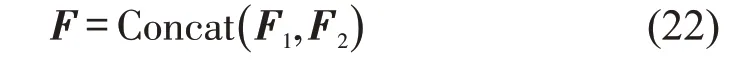
将F展平后得到尺寸大小为986×1 的列向量，然后，连接两层神经元个数分别为10 和2 的全连接层对特征融合信息进行聚合，最终，输出客流量预测值Yt。

3 实验与结果分析

3.1 数据描述及数据预处理

本文选择上海市地铁2 号线虹桥T2 航站楼站和虹桥高铁站作为实验对象，两站点由于接驳飞机和高铁两大交通主体，进出站客流量具有很强的不稳定性和随机性，准确预测两站点客流量有较强的现实意义。向虹桥枢纽管理中心调取两站点2021年1 月1 日～12 月31 日全年的进出站实时刷卡数据，选取每天6:00-22:30 作为研究对象。短时客流预测选择的时间粒度通常为5，10，15，30 min不等，为满足预测的实时性需求，本文预测每5 min 进出站客流，将每天划分为198 个时间步。此外，节假日期间客流波动剧烈，且其他交通方式排班计划变化较大[16]，会影响模型预测效果，同时，考虑到本文将研究客流周周期性对客流预测的影响，因此，将数据集中包含节假日的整周客流数据予以剔除。对原始数据进行归一化处理，选择min-max方法将原始数据映射到[0,1]区间上，即

3.2 评价指标选择

本文采用平均绝对误差(RMAE)和均方根误差(RRMSE)两个评价指标评价各个模型的预测性能。RMAE表示预测值与真实值之间绝对误差的平均值，RRMSE表示预测值和真实值之间偏差的样本标准差。计算式分别为

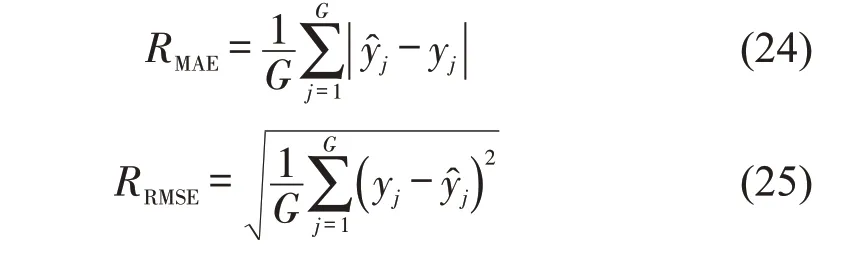
式中：yj和̂分别为第j个测试样本的真实值和预测值；G为测试样本数量。

3.3 模型配置

3.3.1 超参数设置

本文使用Python语言进行程序编写，基于深度学习框架Keras 和Tensorflow 搭建客流预测模型，实验采用的GPU型号为Tesla T4，显存大小为16 G。为提升训练效果，运用shuffle方法将训练集中的数据随机打乱并进行批处理操作。将buffer_size 设置为10000，批量大小设置为128，模型损失函数为RMAE，优化器选择RMSprop，学习率为0.001，激活函数均为ReLU函数。

3.3.2 参数调优

本文使用T2 航站楼数据集开展参数调优实验，对各周期时间片段大小(即参数w、d、n)、GRU 层层数L1、Conv-Transformer 层层数L2以及自注意力头数量p进行调优。各参数的取值范围设置如下：n=(6,8,10,12,14,16,18,20,22,24,26,28,30 )；w∈[1,3] ；d∈[1,6] ；L1∈[1,3] ；L2∈[1,8]；p∈[3,8]。使用评价指标RMAE和RRMSE衡量参数取值对模型性能的影响。实验采取控制变量原则，每次只调整一个参数，其他参数均保持不变，寻找到最优值后，该参数取值将固定，并进行下一个参数的寻优。

为更好地展示实验过程，将实验划分为两个步骤：首先，将L1、L2、p随机固定为2、4、5，对w、d、n进行调优；然后，再调整L1、L2、p取值，直到所有参数被优化。具体过程如下。

Step 1w、d、n调优

将n值设置为12，d值设置为3，改变w取值，依次进行3 次实验，选取最佳的w值并固定大小。以此类推对d和n进行调优，实验结果如图10 和表1所示。

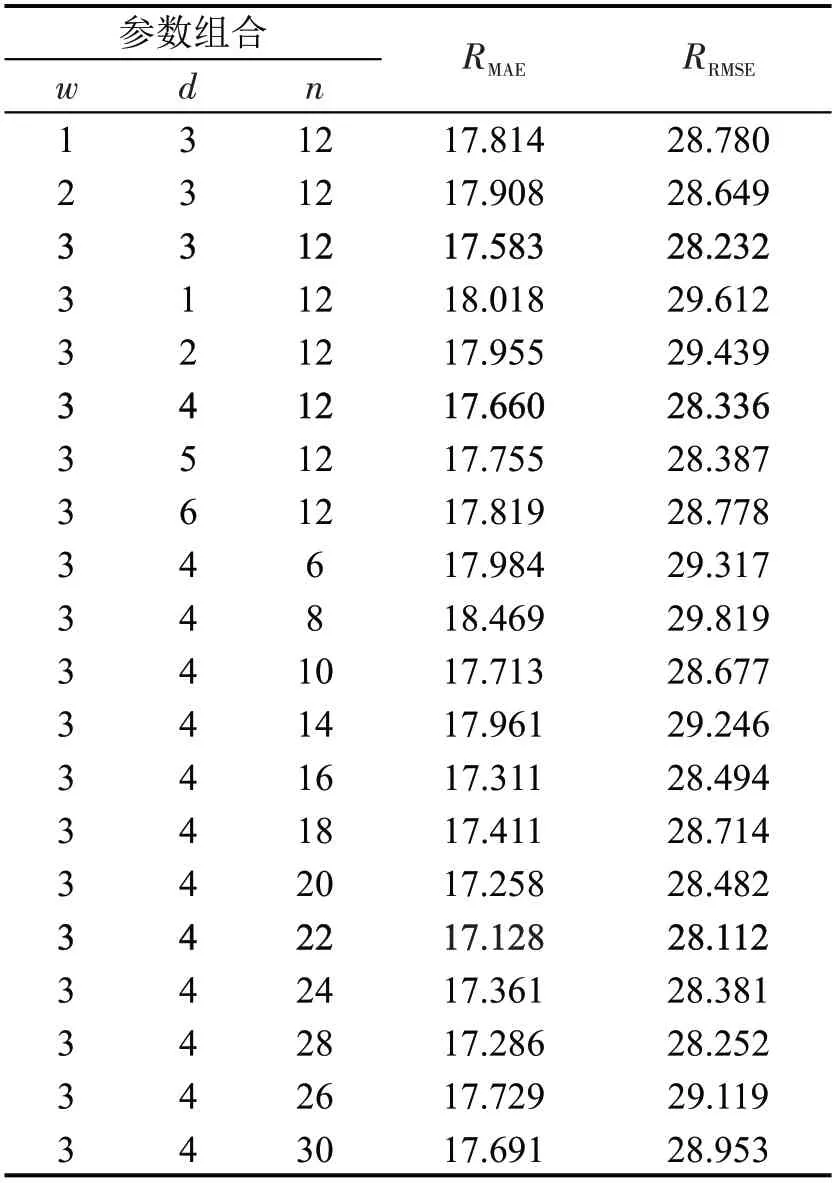
表1 参数w、d、n 调优结果Table 1 Results of parameter w、d、n tuning

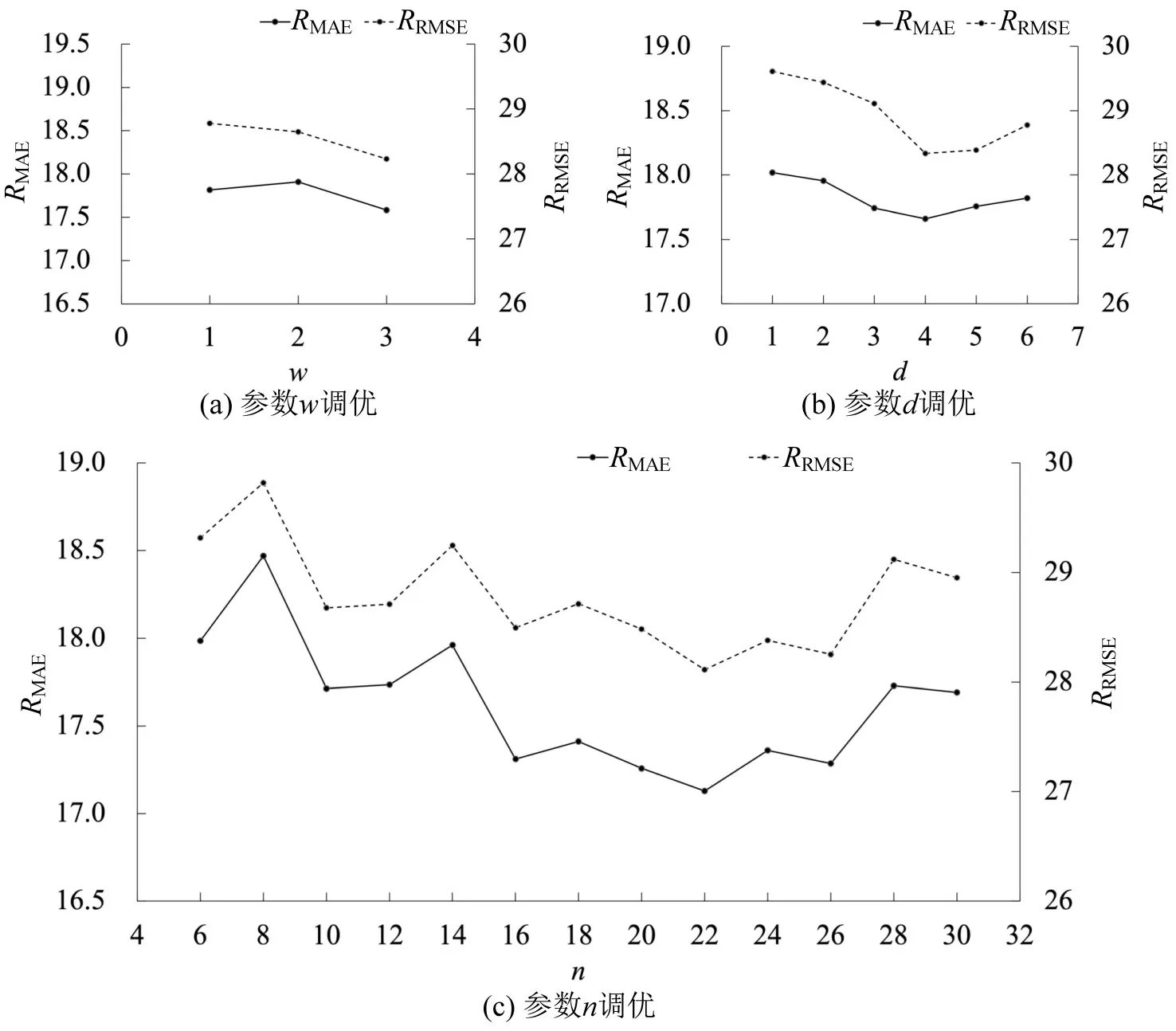
图10 参数w、d、n 调优过程Fig.10 Process of parameter w、d、n tuning

如图10所示，当w=3 时模型预测误差最小，d由1 增加到6 时，预测误差呈现出先下降后上升的趋势，d=4 时达到最小，说明客流周期性特征对预测效果具有较大影响。n由6增加到30时，预测误差整体上呈现先下降后上升趋势，当n=22 时预测误差达到最小。同时，当n取20、22、24 时误差均维持在较低水平，说明大约2 h 内的历史客流对后续客流影响较大。综上，当w=3，d=4，n=22 时模型性能最好，将该参数组合用于Step 2。

Step 2L1、L2、p调优

为确定适当的模型结构，分析隐含层和自注意力头数量对模型预测的影响，依次对参数L1、L2、p进行调优，实验过程同Step 1。结果如图11和表2所示。

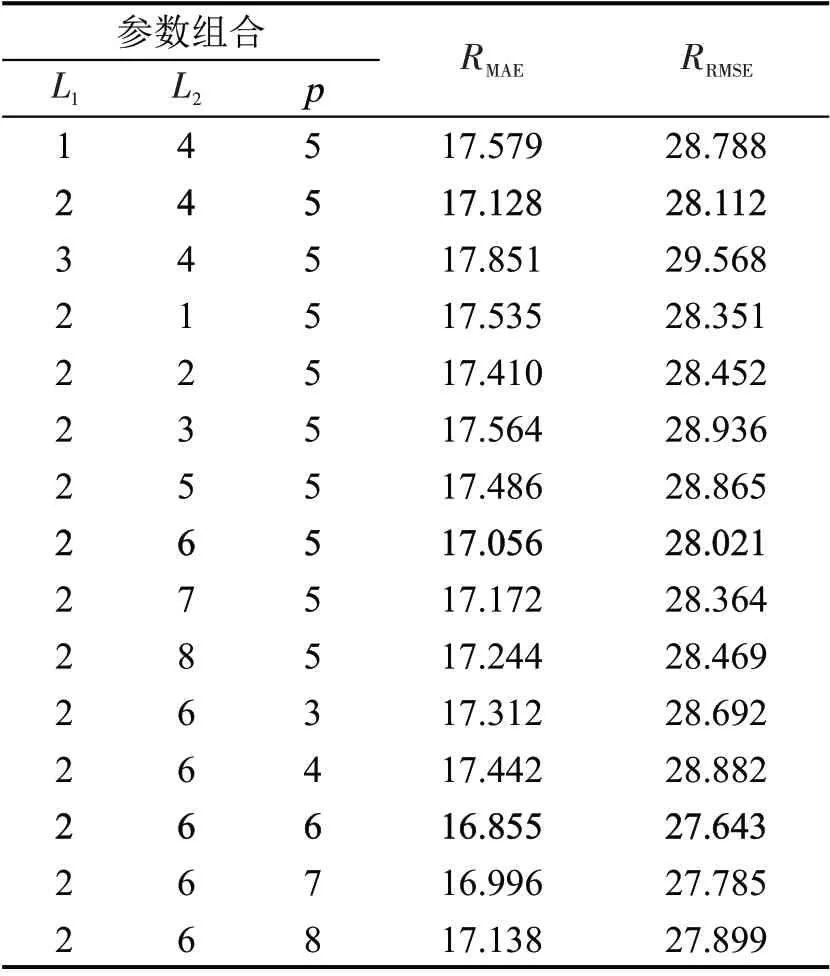
表2 参数L1、L2、p 调优结果Table 2 Results of parameter L1、L2、p tuning

由图11 可知：(1)当L1=2，即GRU 层层数为2时，模型预测效果显著提升，而由2增加至3时预测效果变差；L2由1 增加到8 时，模型预测效果存在波动，当L2取6 时，预测误差最低，上述现象说明，模型隐含层层数对预测性能有较大影响，虽然隐含层增多理论上可以提升模型表达能力，但层数过多会引起模型过拟合，导致预测结果不佳。(2) 当p由4增加到6时，模型误差有明显下降，继续增加至7和8时，误差逐渐提升，说明自注意力头数量对模型预测有一定影响，在设计模型结构时，应选取恰当的数值以避免影响预测精度。

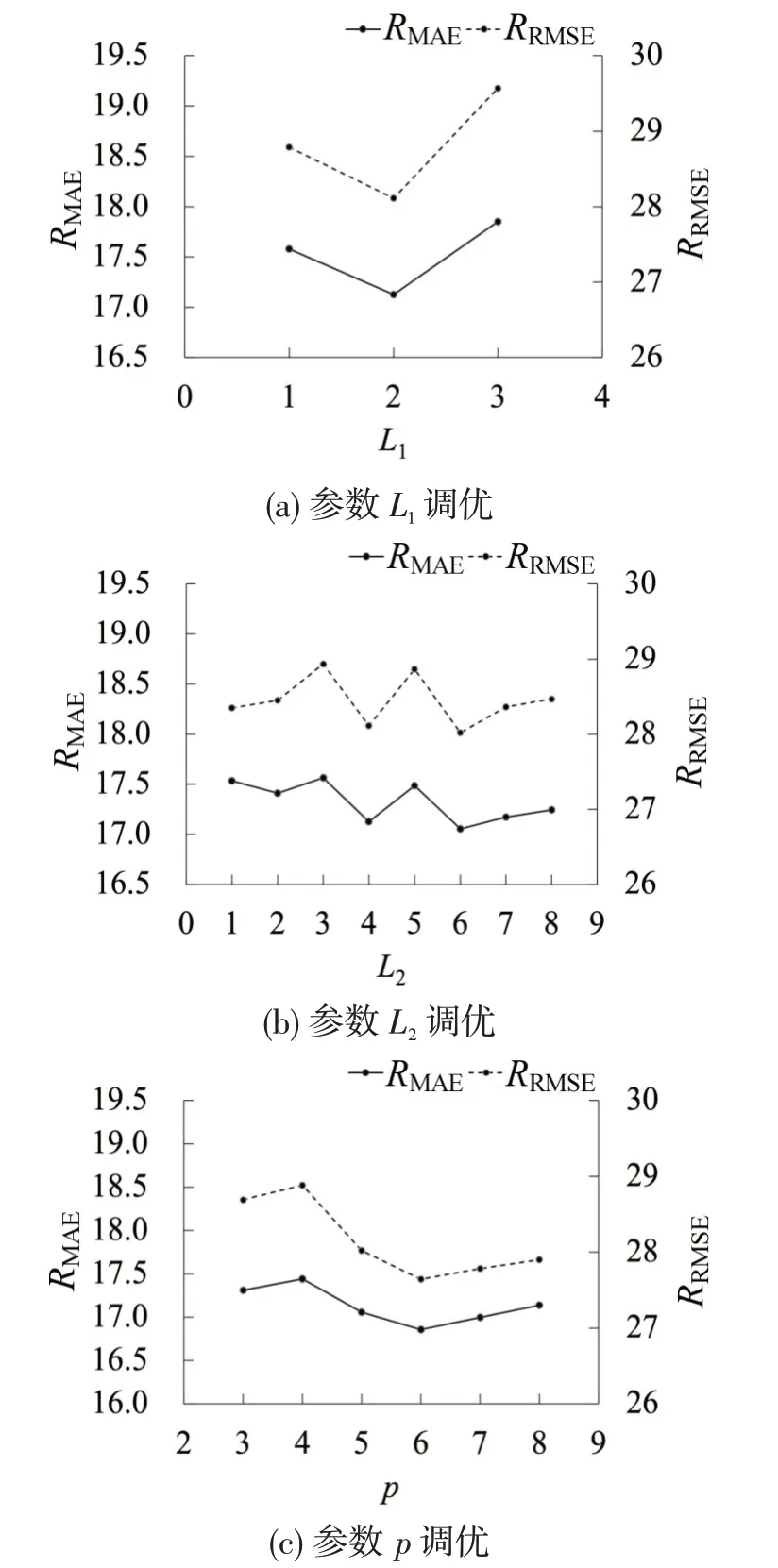
图11 参数L1、L2、p 调优过程Fig.11 Process of parameter L1、L2、p tuning

综上所述，本文通过调参实验确定最优参数组合:w=3，d=4，n=22，L1=2，L2=6，p=6。此时RMAE和RRMSE分别为16.855 和27.643，相较于其他参数组合RMAE和RRMSE值至多下降8.74%和7.30%。

3.4 模型性能评估

本文使用航站楼站和高铁站两数据集来评估GRU-Transformer 模型的预测性能，并将结果与5种基线模型(BPNN、CNN、GRU、CNN-GRU、Transformer)进行比较。同时，为进一步探究模型各组件对预测性能的影响与改进方法的有效性，进行了模型消融实验。各模型结构描述如表3所示，其余参数设置均与GRU-Transformer 模型保持一致。实验结果如表3所示。

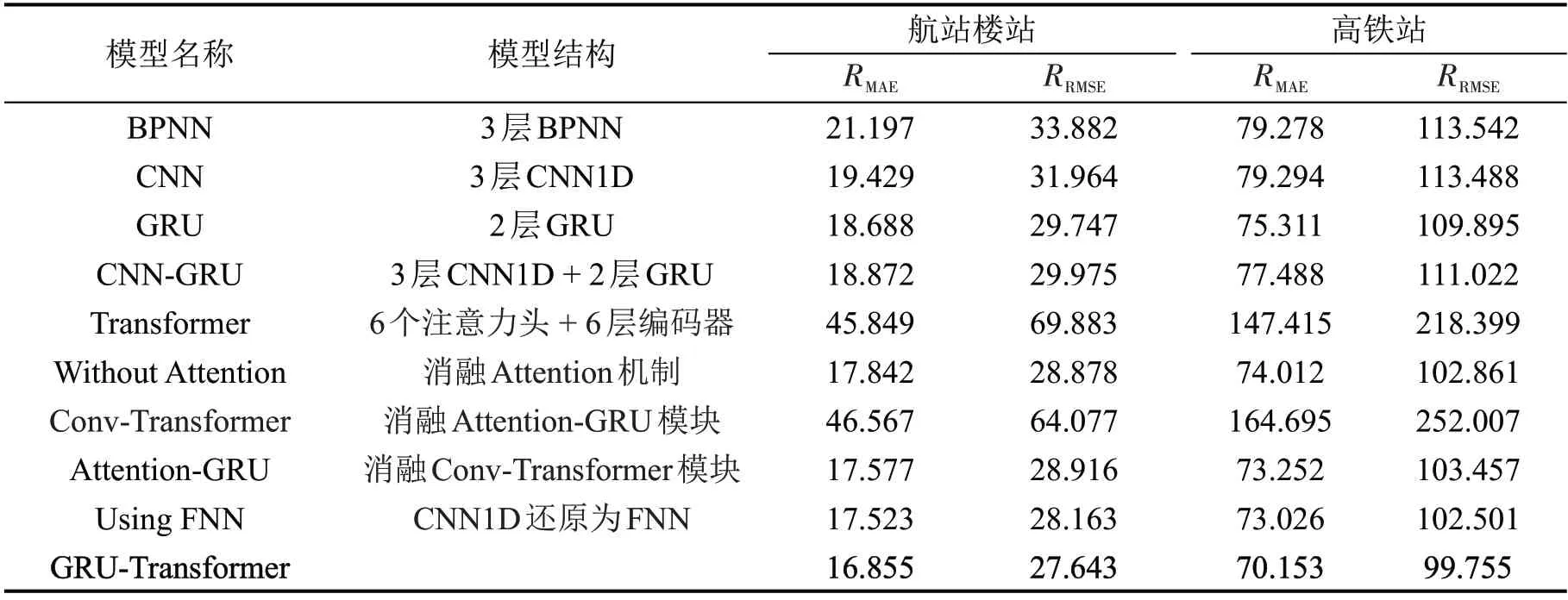
表3 模型对比结果Table 3 Model comparison results

通过分析表3 可知，GRU-Transformer 模型在两站点进行客流预测时，RMAE和RRMSE值均低于其余基线模型，拟合效果最好。对比次优基线模型GRU，GRU-Transformer 模型在航站楼站数据集中RMAE和RRMSE值分别下降9.81%和7.07%；在高铁站站数据集中RMAE和RRMSE值分别下降了6.85%和9.22% 。 这说明，相较于基线模型，GRUTransformer 模型的预测结果与真实值之间的误差更小，整体性能有较大提升。同时，GRUTransformer 模型在航站楼站与高铁站两个不同场景下均取得最优的预测性能，说明该模型对不同数据集的适应能力较强，在进行客流预测时能够保持较好的鲁棒性精度，证明了其实用价值。此外，值得注意的是，将Transformer 模型单独用于客流预测时，在两个数据集中预测性能均远远低于其他基线模型，说明Transformer 由于其非循环网络结构无法有效识别客流输入顺序的缺陷，导致单一的Transformer不能很好地拟合客流数据连续性特征，因此，将其用于客流预测时必须加以改进优化。

对比消融模型，可以看到：(1)相较于注意力机制消融模型，所提出模型的RMAE和RRMSE均有所下降，说明Attention-GRU 模块中的Attention 机制可以有效捕捉各时间步输入序列对模型预测的影响程度，增强该模块拟合数据连续特征的能力。(2)Conv-Transformer 模型虽然将Transformer 中的FNN层改进为CNN1D，但依然存在结构上的缺陷，导致预测误差严重偏离正常范围。观察具有GRU与Transformer 并行结构的注意力机制消融模型、还原FNN模型以及GRU-Transformer模型，可知预测误差均恢复正常水平，这说明将GRU 与Transformer 并行的策略能够极大程度上消除上述结构缺陷，使得Transformer 可以更好地应用于客流预测中。(3)与Attention-GRU模型相比，所提出模型性能在两数据集上均有提升，说明两个模块的特征挖掘有较强的互补性，引入Transformer 可以使模型更好地拟合数据不同维度特征。(4)与还原FNN 模型相比，所提出模型性能有小幅度提升，说明将Transformer 用于时间序列数据处理时，CNN1D层相比FNN层有一定优势。

3.5 预测效率评估

为评估GRU-Transformer 模型预测计算效率，验证其短时客流预测时效性与实用性，本文将5个基线模型与GRU-Transformer 模型分别进行连续10 次客流预测，并计算单次预测平均时间，结果如表4所示。

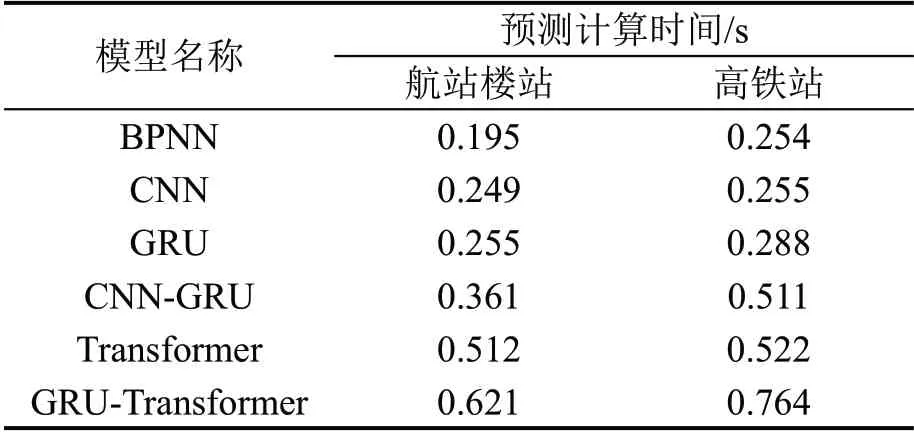
表4 模型计算效率Table 4 Model computational efficiency

由表4 可知，GRU-Transformer 模型由于结构复杂度提升较大，因此，预测计算时间相较于各基线模型略有增长，但是，综合考虑该模型在预测准确度方面的较大提升，其预测效率的降低幅度总体处于可接受范围内。同时，GRU-Transformer 模型在两个数据集下单次预测平均计算时间均小于0.8 s，说明其能够充分满足短时客流量预测的时效性要求，可以实际应用于客流滚动实时预测。

3.6 预测结果可视化

为进一步展示模型预测效果，选取2021 年10月21 日(周四)和10 月23 日(周六)航站楼站真实进出站客流和预测进出站客流进行可视化，结果如图12 所示。可知，GRU-Transformer 模型在工作日和休息日均有良好的预测表现，可以较为准确地拟合客流变化趋势及峰值。同时，预测值与真实值可视化曲线之间的离散程度较小，预测偏差波动不大，直观上体现出预测结果良好的稳定性。对于工作日进出站客流，由于乘客日常通勤和出行习惯产生的客流“双高峰”特点十分明显，模型可以精确拟合客流高峰时段，并且对客流峰值的预测效果较好。观察休息日进出站客流可以发现，相比于工作日，客流不存在十分明显的高峰值，起伏的范围不大，然而由于客流波动非常频繁且剧烈，模型对峰值的拟合效果略有欠缺，但仍可以准确拟合客流态势，不存在严重的偏离现象。

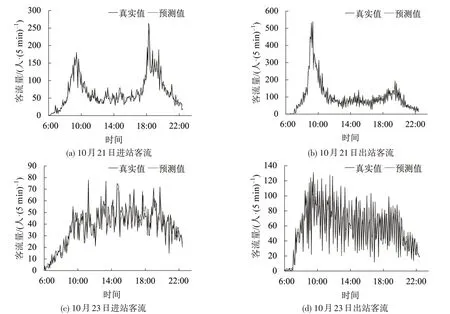
图12 10月21日和10月23日真实客流与预测客流对比Fig.12 Actual and predicted passenger flow on October 21 and 23

综上所述，本文所提出的GRU-Transformer 模型能够实现准确的城市轨道交通短时进出站客流预测，并且可以满足每5 min 更新1 次客流量预测值的实际需求，具有较好的实用性。在实际应用中，通过比较客流预测结果与客流预警阈值大小产生相应的预警等级，可以为站点的运营组织和应急响应提供有力的决策支持。

4 结论

为适应城市轨道交通客流变化具有强周期性和连续性的特点，本文提出客流多时间尺度特征建模方法，构建了一种基于GRU 神经网络与Transformer 模型的城市轨道交通短时客流预测模型。在两个真实数据集上开展调参实验和模型对比实验，结果表明：

(1) 对于时间片段参数w、d、n、Attention-GRU 与Conv-Transformer 模块隐含层层数L1、L2以及自注意力头头数p，实验获得最优参数组合：w=3，d=4，n=22，L1=2，L2=6，p=6。该过程使得模型RMAE和RRMSE值至多下降了8.74%和7.30%，说明各周期时间步长以及隐含层层数均对模型预测有较大影响，同时，也证明了多时间尺度特征建模的有效性。

(2) 相比BPNN、CNN、GRU、CNN-GRU 和Transformer 这5 种基线模型，GRU-Transformer 模型具有最佳的预测性能，相比次优模型GRU，RMAE值在两数据集上分别下降9.81%和6.85%；RRMSE值在两数据集上分别下降7.07%和9.22%。

(3)相比各消融模型，GRU-Transformer模型预测精度最高，进一步证明本模型将GRU 和Transformer 并联的网络结构具有良好的复杂函数拟合效果，不仅在很大程度上弥补了Transformer模型非循环结构的缺陷，还可以将两模块分别捕捉的连续性、周期性特征有效地进行互补。

(4)本文实验算例选取了上海市地铁2 号线虹桥T2 航站楼站和虹桥高铁站作为研究对象，对于此类与民航、铁路等外部交通方式接驳的城市轨道交通站点，进出港航班、到发列车的数量与不确定性等因素对客流量也具有一定影响。本文未针对此类外部因素进行特别建模，且模型对休息日客流量峰值的拟合效果仍有待提升。在后续研究中，我们将综合考虑枢纽集散影响与更全面的交通枢纽客流预测参数，以期进一步提升模型拟合能力。