基于斯坦科尔伯格模型的农产品供应链动态博弈问题

王俊春 段 丹 李凯敏 张宇雁

（1.保山学院；2.保山技师学院 云南保山 678000）

农民合作社的发展现状

从图1和图2可以看出：2012-2020年，从总量来看，合作社数量和入社农户数逐年增长并在2018年达到峰值，2019年出现下降后继续增长；从同比增速来看，合作社数量和入社农户数，在2015年达到增速峰值后均下降，2019年触底反弹；从合作社构成来看，农产品类平均占比为86.76%，合作社的经营内容主要是农产品生产和供给。而从政策层面进行梳理可以发现，2015年颁布的《关于深化供销合作社综合改革的决定》从创新农业生产服务方式和手段、提升农产品流通服务水平、打造城乡社区综合服务平台、稳步开展农村合作金融服务等方面构建起农民合作社发展的良好政策环境（包括土地、信贷、财政补贴等政策利好），这成为农民合作社发展的重要变量（冯春、杨玄，2020）。2019年，11个部委针对农民合作社进行“空壳社”专项清理，而这一年也出现了合作社发展史中罕见的数量骤减（减少了13755个）。随后颁布了《供销合作社促进小农户和现代农业发展有机衔接工作实施方案》《关于规范发展供销合作社金融服务的指导意见》《关于推进区域电商发展的实施意见》，从引导小农户开展合作与联合、创新合作社组织小农户机制、增强农村电商服务带动小农户能力、提升金融服务小农户水平等方面进一步优化了农民合作社的发展空间，而对应的在2020年数量和增速均呈现出增长态势。可以看出，农民合作社的发展与政策变量紧密相关。作为相关政策执行者的地方政府和合作社之间的利益博弈贯穿合作社发展的整个历程。

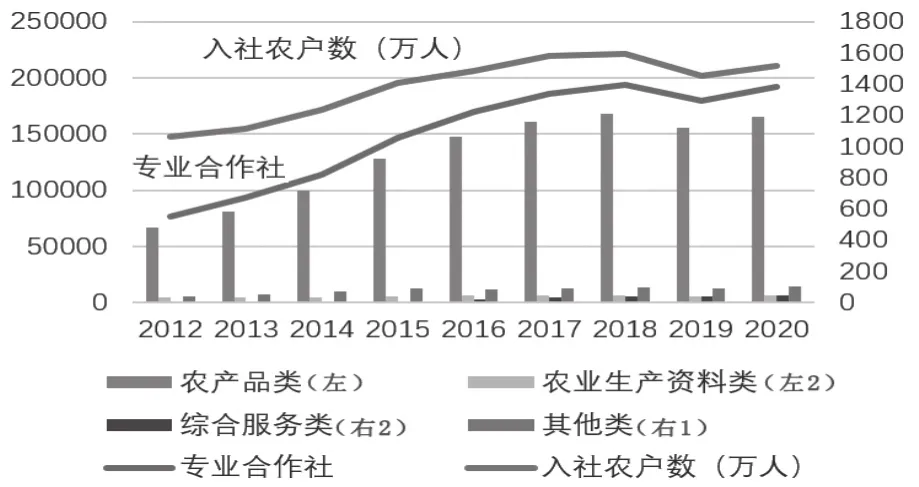
图1 全国农民专业合作社总体情况

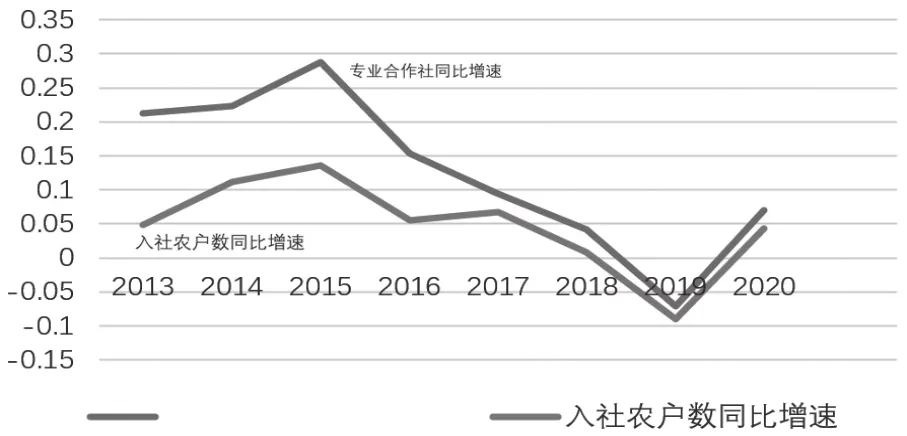
图2 专业合作社、入社农户数同比增速情况

农产品供应链中“地方政府-农民合作社”的动态博弈模型

（一）基本说明

从公共选择理论的角度假设：第一，农户对农民合作社服务的需求为“有效需求”；第二，供给层面中中央政府设定为政策制定者，为利益偏好中性，地方政府设定为政策执行者（利益主体），有自身的利益诉求，以专业大户为主的农民合作社设定为一个利益主体；第三，供给层面的两个主体：地方政府和合作社都为“理性经济人”。

（二）模型分析

1.基本假设。根据模型，做出如下假设：第一，有一个地方政府G和两个合作社B1和B2，不同合作社有不同的经营效率；第二，Bi（i=1，2）作为提供合作社服务的供给主体，总收益包括经营收益和社会收益，且Bi有决定这两种收益多少的能力和偏好；第三，G有选择Bi（i=1，2）上缴一定比例的经营收益和社会收益的权力；第四，社会收益和经营收益具有同质性，可以通过货币化来衡量；第五，G和Bi（i=1，2）的目标效用函数都遵循边际收益递减规律。

2.变量说明。xi：Bi（i=1，2）获得的经营收益；yi∶Bi（i=1，2）获得的社会收益；αi：G选择Bi（i=1，2） 上缴的经营收益比例；1-αi∶G选择Bi（i=1，2）上缴社会收益的比例，其中变量中的i=1，2。

3.斯坦科尔伯格模型建立及分析。地方政府守信，农民合作社之间形成合作。

先讨论第一种情形，G与Bi的动态博弈顺序为：Bi（i=1，2）选择各自的收益水平（经营收益和社会收益）x1，y1和x2，y2；G 选择Bi（i=1，2）两种收益的上缴比例α1、1-α1、α2、1-α2，其中，α1为B1的经营收益，1-α1为其社会收益；α2为B2的经营收益，1-α2为其社会收益（张维迎，2019）。

在地方政府和合作社的完全信息动态博弈中，Bi是领先者，G是尾随者。G并不能先决定Bi（i=1，2）在合作社运营管理过程中的收益水平，而是Bi在实际经营过程中先获得自身的经营收益和社会收益。而对于Bi，它们达成彼此合作以期获得总目标效用函数的最大值。均衡解则由两个条件来决定：第一，给定Bi（i=1，2）收益，G追求收益最大化；第二，G的反应函数既定，Bi（i=1，2）追求收益最大化。而要求解纳什均衡，需要解决两个问题：给定Bi（i=1，2）收益水平（xi，yi，i=1，2）时，G的反应函数的求解；给定G的反应函数，Bi的经济收益和社会收益为多少。

若 G是“平均主义”的地方政府，即偏好两个合作社上缴收益相同。对于地方政府G这个利益主体而言，其寻求Bi（i=1，2）上缴的总收益形成的目标效用函数最大化。G的总目标效用函数为：

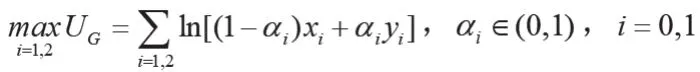
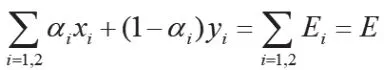
通过上述分析得出地方政府G的反应函数，现分析Bi的目标效用函数最优化问题。斯坦科尔伯格模型中Bi作为领先者，假设其不合作，寻求各自的收益函数最优化，B1的目标收益函数：

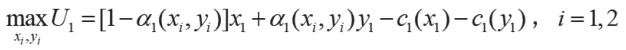
其中，c1(x1)，c1(y1) 分别为B1在创造两种收益所发生的成本，设，其中，a1、b1均为劳动成本系数，而该式遵循边际成本递增规律，经整理得：，i∈1，2。同理可得B2的目标效用函数。

若Bi合作，则总目标效用函数为：

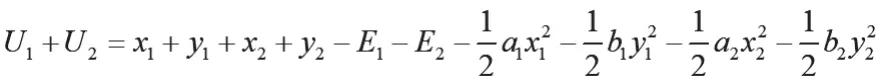
结合上述推导，纳什均衡上缴比例为：

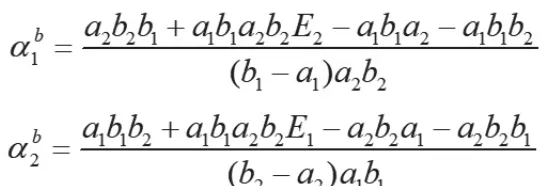
纳什均衡的上缴比例对于地方政府G目标效用函数来说是最优解。对于总的合作社目标效用函数最优化求解，Bi的收益函数及上缴比例受到另一个合作社的影响，因此，均衡解是包含了外部效应的最优解。同时，该种情形下的收益函数不会发生囚徒困境式的“收益损失”，但这种情形不具备客观现实性，是一种理论分析的最优解。

农民合作社之间不合作，地方政府不守信。Bi（i=1，2） 寻求自身效用函数最优化，不考虑其收益水平的外部性问题，也就是说，合作社Bi=（1，2） 的经营收益和社会收益是会受到另一个合作社Bj（j=1，2）的影响。假设Bi先行动，G后行动。Bi不合作，纳什均衡解可定义为：给定Bi的反应函数，G的选择是最优的；给定地方政府和Bj（j=1，2） 的选择，Bi（i=1，2，i≠j）的选择最优。

先求解第二阶段博弈纳什均衡解：给定α1，α2和x2，y2，B1选择x1，y1。B1的目标效用函数为：，i∈1，2。计算得：

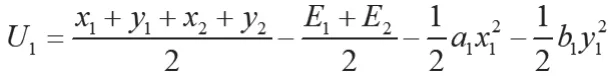
同理可得B2的目标效用函数。求偏导可得：

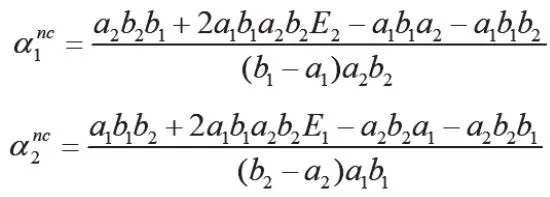
将该结果和第一种情形相比较可以发现，“农民合作社之间不合作、地方政府不守信”情形下合作社创造的收益均小于“农民合作社之间合作，地方政府守信”情形的结果。G更偏好较高的收益上缴比例。在G不守信情形下，上缴比例大于参照系的最优纳什均衡解，产生这种结果的原因主要包括：该种情形下，Bi的策略选择不会考虑另一个农民合作社的外部效应，而根据反应函数，Bi之间的收益函数及上缴比例是存在相互影响的；同时，因存在外部效应，Bi都理性地选择策略，则产生“囚徒困境”式的“收益损失”。

地方政府守信，农民合作社之间不合作。如果地方政府G先行动，选择Bi（i=1，2）收益的上缴比例α1，α2，并且信守事先签订的分享合同；Bi则随后行动，同时选择收益水平x1和y1，x2和y2。那么，纳什均衡解为：给定合作社反应函数，地方政府G的选择是最优的；给定G 和第j 个合作社的选择，第i个合作社的选择最优。

已知，合作社B1的目标效用函数为：。当Bi相信G信守承诺——上缴比例不发生变化，那么，B1的最优解条件为：，进而可得：x1c=(1-α1)/a1，同理也可得：y1c=α1/b1。同理，合作社B2的最优选择是：x2c=（1-α2）/a2，y2c=α2/b2。G 的效用函数则为：，αi∈（0，1），i=0，1。因此，可构造拉格朗日函数为：

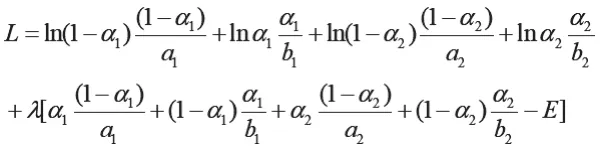
进而得：

预算约束条件则为：

求解得最优解α1c和α2c，但因涉及三阶多项式，得出精确结果较为困难，但就目标而言，无需解出α1和α2具体值，只需比较守信和不守信的不同情形。先比较情形一和情形三，可以发现：x1c＜x1b，x2c＜x2b，其中，xic是指政府守信情形。同理可得：y1c＜y1b，y1c＜y1b。因此，地方政府守信情形对应的收益水平小于情形一的收益水平。又α1c＜1/2，α2c＜1/2，因此，α1c＜α1nc，α2c＜α2nc。结果为：1/2a1=x1nc＜x1c，1/2b1=y1nc＜y1c，1/2a2=x2nc＜x2c，1/2b1=y1nc＜y1c。所以，相较于不守信情形，地方政府G信守承诺，则Bi（i=1，2）创造的经营收益和社会收益更多收益。虽信守承诺情形结果不等同参照系（最优解），但却是最为接近的收益水平。

综上分析，可得如下结论：第一，G守信和G不守信两种情形都会产生“收益损失”；第二，与地方政府G不守信情形相比，守信情形因不存在外部效应，会创造更高收益水平。

进一步讨论。地方政府G守信的制度设计部分解决了G不守信情形中的激励问题，但为什么在现实情形中，G却选择不守信呢？主要有两方面原因：一方面，制度设计中并没有严格规定地方政府在违背事先声明的分享合同要受到相应的惩罚，而这一制度缺陷给政府背信提供空间；另一方面，G不守信情形下的上缴比例多于G守信情形下的上缴比例，所以，从这点来看，G没有动力守信，而这点是最为主要的原因。而这种情况，将其称之为地方政府G 的政策动态非一致性。

假定地方政府G事先选择一个最优的上缴比例，且这个比例低于守信时的比例，当农民合作社Bi创造自身的收益水平时，地方政府G有动力去改变事先的上缴比例。马骏认为：“这种政策选择是动态非一致性的，这样的策略选择常常使理性决策的农民合作社Bi难以置信（Jun Ma，1995）。”

若地方政府和合作社的动态博弈顺序为：地方政府G先选择 Bi（i=1，2）的上缴比例αi；合作社Bi信任G的事先承诺，选择最优反应函数。Bi的最优反应函数为：。而G的目标效用函数最优解条件为：。当方程式满足时，G会守信，也就是维持事先选择的上缴比例αiO，i∈1，2，而这个上缴比例是动态一致性的。但上缴比例低于守信政府G情形的最优政策是否是动态一致性的？结合上述推导，可得到下列等式：

若要该使等式成立，即若满足动态一致性，下列式子必须成立：α1O=α2O，进而要求a1=a2且b1=b2，也就是说只要存在a1≠a2，b1≠b2情况时，最优政策将是动态非一致性。但根据变量界定，a1，a2，b1，b2是反映合作社服务政策执行过程中发生的劳动成本系数，即反映农民合作社提供的合作服务的效率水平，在客观现实中，通常Bi（i=1，2）的效率水平是不同的，也就是说：a1≠a2，b1≠b2。所以，地方政府G的最优政策将是动态非一致性的。不守信成为地方政府G在合作社服务供给过程中利益博弈的理性选择。

农民合作社合作服务政策动态非一致性问题的纠偏策略

（一）地方政府注重自身的良好声誉，将有利于其选择守信策略

前文的斯坦科尔伯格模型分析的是一次性博弈，在该博弈过程中，地方政府寻求目标效用函数最大化，农民合作社则相信地方政府有动力改变事先声明的上缴比例，因此，最优的策略就是“假合作社”“翻牌合作社”“一次性合作社”。但是，假设该动态博弈是无限重复博弈模型，地方政府也注重自身良好声誉。那么，在无限重复博弈中，地方政府的策略可描述为一系列上缴比例：{α1，α2}，农民合作社i的战略选择为：{(x1，y1)，(x2，y2)}。

假设t表示无限重复博弈的次序中的第t次，其中t=1，2，…，第t-1次的博弈过程可以看作是第t次动态博弈开始之前的一次性博弈，每次的一次性博弈过程中，每个参与者的收益均为现值，设折现率为ξ，且ξ为定值。

设农民合作社在第t阶段的收益水平为(xt，yt)，地方政府选择上缴比例为αt。

则农民合作社的策略为：

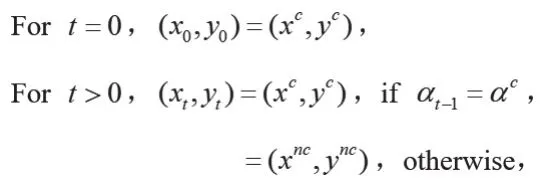
地方政府的策略为：

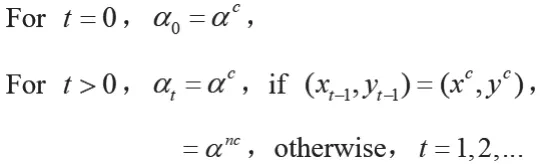
农民合作社如果有“地方政府是守信的”预期，那么，合作社创造的收益水平为(xc，yc) ；若有“地方政府是不守信的”预期，合作社创造的收益水平为(xnc，ync)。进一步来看，当地方政府在每次的一次性博弈中都选择守信策略，那么农民合作社之间也会选择合作策略，从而创造更高的收益水平。只要地方政府在第t阶段偏离了守信策略情形的纳什均衡，则农民合作社会在第t+1阶段会选择不合作策略，对应(xnc，ync) 的收益水平。同样的，地方政府选择守信策略，上缴比例选择αc，也是预期到农民合作社都会选择收益水平(xc，yc)，否则，地方政府则会选择αnc的上缴比例。

若初始值为(x0，y0)=(xc，yc)，上缴比例α0=αc。下面将证明满足地方政府选择守信策略进而形成双方合作博弈的条件是存在的。

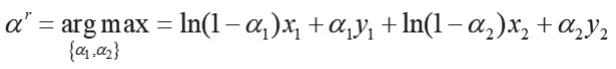
（二）“仁慈的”地方政府的角色效能将会对合作社产生正向激励

如果地方政府是“仁慈的”，亦即地方政府不考虑自身效用水平，而是“利他地”考虑到农民合作社的效用水平，因此而推导出的结论也将会大不相同——与“经济理性人”假设相比。特别地，地方政府选择不守信策略的情形中，在“仁慈的”地方政府的假设前提下会得到纳什均衡解，推导过程如下所示。

设地方政府寻求两个农民合作社效用函数最大化，则地方政府的目标效用函数为：

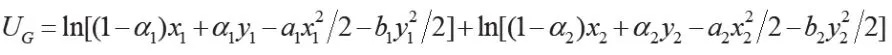
地方政府的最优解：

同理可得：

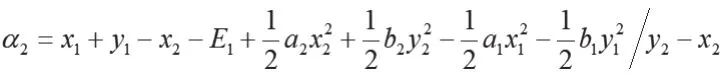
假设两个农民合作社之间是不合作的，则其面临的情形与上述情形一样，亦即合作社i（i∈1，2）都寻求自身效用函数最大化。依据反应函数，农民合作社1的效用函数为：，推导可得：。

可以看出，上述结果相当于地方政府一次性收缴了一部分收益。在这种一次性收缴部分收益的制度设计中，地方政府的问题就变成选择两笔一次性收缴部分收益寻求效用最大化：

其中，Ti(i∈1,2) 表示在合作服务供给中地方政府选择的农民合作社i 一次性上缴的部分收益。因此，合作社B1选择x1，y1，得到效用最大化水平。同理可得，合作社B2选择x2，y2，得到效用最大化水平。

当“一次性上缴部分收益”成立，那么，上述结果是最优的，而“仁慈的”地方政府的制度设计也会使其获得的收益水平最优。在这个假设条件下，即便是地方政府不守信，也就是地方政府在农民合作社创造收益之后选择上缴比例，但也不会像在“平均主义的”地方政府情形下导致对农民合作社创造更多收益激励不足时出现的问题。因此，在对农户提供合作服务供给中，地方政府应该更多地考虑农民合作社的整体收益水平而不仅仅纠结于地方政府与合作社在收益分享的分配问题。在未来的制度设计中，寻求缴后盈余收益的平均化的制度设计（在模型中，假设两个合作社缴后的收益相等）应减弱，相反，制定更宽泛的上缴标准将有利于获得更多收益。

（三）打破合作服务供给“平均主义”思维，形成差别化合作社收益激励规则

若地方政府任命的供销社主管官员选择α1和α2的上缴比例，寻求自身目标效用函数最优解：

而满足条件为：

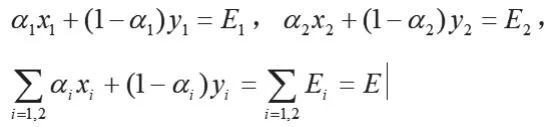
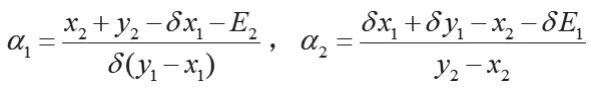
进而可以推导得出：

求偏导又可得：

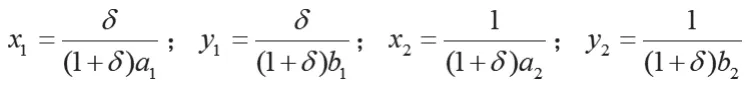
因此：

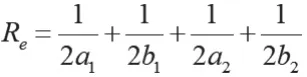
当a1＜a2，b1＜b2，δ＞1，较易可得：Re＜Rne。

因此，与“平均主义的地方政府”相比，在任命一个“平均主义不太强烈”的主管官员情形下农民合作社会创造更高的收益水平。在“平均主义的地方政府”情形下，赋予农民合作社1（效率水平较高）和农民合作社2（效率水平较低）相同的上缴比例，且给予两个合作社相同的政策优惠，“大锅饭”式的思维往往造成效率高的合作社没有动力创造更多收益，同时，如果上缴比例设置不合理，对效率低的合作社也会造成不良影响。在“平均主义不太强烈”的情形下，农民合作社1将有动力创造更多收益，因为政策将为其提供更好的有利条件，从而合作社1创造的总收益将会增加，虽然合作社2的收益会减少，但总的来看，增加量会超过减少量。在“平均主义不太强烈”的主管官员情形下，农民合作社1的收益L1会高于合作社2的收益L2。但是也发现，任命一个“平均主义不太强烈”的主管官员并不能从根本上解决前文所述的“政策的动态非一致性”问题，但这样的制度设计（亦即L1≠L2）可以减少“地方政府不守信”对农民合作社创造更高收益水平所产生的消极作用。总之，该种制度（L1≠L2）会使地方政府获得更高的上缴收益。