多层串联棱锥台楔形机构组合式缓冲器运动分析

魏延刚，武树暄，司马娅轩，张 媛，宋亚昕，王睿嘉

(1.大连交通大学 机械工程学院，辽宁 大连 116028；2.大连科技学院 机械工程学院，辽宁 大连 116052； 3.北京多邦汇科轨道车辆装备技术有限公司，北京 101100)

热塑性聚酯弹性体(thermoplastic polyester elastomer，TPEE)元件具有良好的综合性能[1-2]，因此TPEE缓冲器近些年来得到越来越多的应用[3]。然而，纯TPEE缓冲器的能量吸收率还达不到TB/T 1961—2016《机车车辆缓冲器》对缓冲器能量吸收率要求的80%[4]。为了进一步提高缓冲器能量吸收率，相关研究人员已经研制了几种楔形机构与TPEE元件组合的组合式缓冲器[5-14]，但对这几种组合式缓冲器的运动学研究不够充分，他们主要研究了楔形机构的受力和效率(摩擦损耗率)，而没有对其位移和摩擦损耗量(能量消耗量)进行研究；同时由于结构的原因，这几种组合式缓冲器对制造和安装精度要求很高，若达不到一定的精度，楔形机构在回弹过程中易出现卡顿，从而将影响到整个缓冲器的回弹性能。针对这些问题，研究人员又提出了楔形机构与TPEE元件组合的新型组合式缓冲器，例如，多层串联棱锥台楔形机构与TPEE组合的组合式缓冲器[15]，本文将简要介绍多层串联棱锥台楔形机构TPEE组合式缓冲器的结构和工作原理，应用经典力学原理全面分析楔形机构的各主要元件的力、位移、功、摩擦损耗率以及楔形机构、缓冲器的能量吸收率，给出缓冲器能量吸收率的计算方法和主要公式，并通过算例验证这种缓冲器计算方法的正确性，为新型缓冲器的研制提供参考。

1 新型组合式缓冲器的构成及工作原理

多层棱锥台楔形机构与TPEE元件组合而成的新型组合式缓冲器(以下简称组合式缓冲器)，其楔形机构由多层相同的空心棱锥台楔形机构串联构成，每层楔形机构由壳体、楔块和空心棱锥台构成，多层相同楔形机构串联成全钢摩擦式缓冲器；壳体、金属隔片和TPEE元件组件构成了TPEE元件缓冲器；心轴、螺母和螺纹联接防松件将全钢摩擦式缓冲器和TPEE元件缓冲器串联成组合式缓冲器。图1为3层棱锥台楔形机构的组合式缓冲器结构示意图。

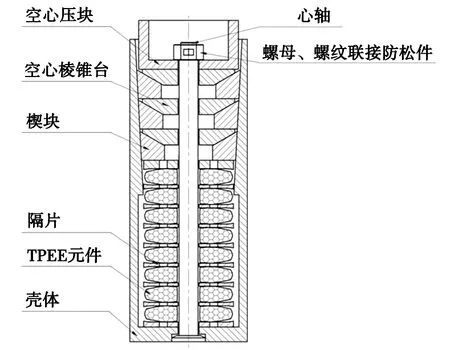
图1 3层棱锥台楔形机构的组合式缓冲器结构示意图

图1中，当冲击载荷沿轴向作用于空心压块上时，空心压块推动顶层的空心棱锥台，空心棱锥台推动顶层楔块，顶层楔块推动中间层的空心棱锥台，中间层的空心棱锥台推动中间层的楔块，中间层的楔块推动底层的空心棱锥台，底层的空心棱锥台推动底层的楔块，底层的楔块推动金属隔片和TPEE元件组件，使载荷通过金属隔片作用在壳体的底部。整个过程中，空心棱锥台侧面与楔块内表面斜平面相互挤压产生相对运动和摩擦，楔块外表面与壳体上腔室内表面相互挤压产生相对运动和摩擦，楔块下表面与空心棱锥台的上表面或最上层金属隔片的上表面相互挤压产生相对运动和摩擦，这些摩擦消耗了能量，从而提高缓冲器能量吸收率。同时，来自最上层金属隔片的轴向力使TPEE元件组件发生轴向压缩变形而吸收冲击能量。在轴向冲击载荷消失后，TPEE元件恢复变形并推动金属隔片、楔块、空心棱锥台和空心压块由下向上运动，最终所有元件恢复到受载荷冲击前的状态。

2 组合式缓冲器的运动学分析

2.1 楔形机构的受力和位移

2.1.1楔形机构的受力分析

2.1.1.1单层楔形机构的受力分析

图2～图4分别为金属隔片、左侧楔块和空心棱锥台的受力示意图。

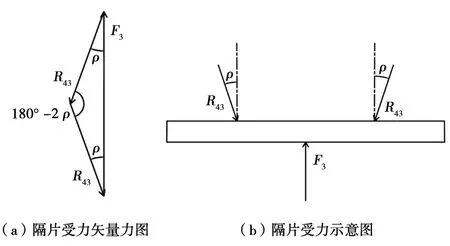
ρ.楔形机构各摩擦面间的摩擦角角度；R43.楔块对隔片摩擦面间的总反力；F3.楔块承受的来自TPEE元件组件的工作阻力。图2 金属隔片受力矢量力图和受力示意图

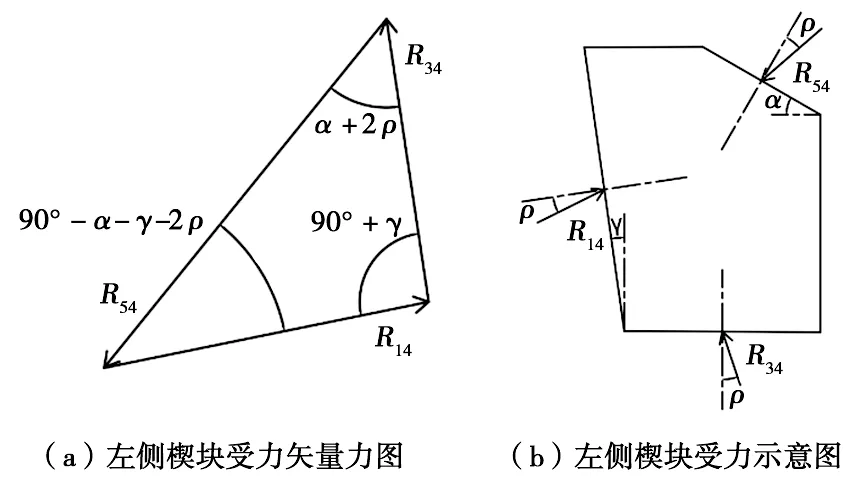
α.空心棱锥台与楔块贴合斜平面与水平面之间的夹角；γ.楔块与壳体贴合斜面与垂直面之间的夹角；R14.壳体对楔块的总反力；R34.隔片对楔块的总反力；R54.空心棱锥台对楔块的总反力。图3 左侧楔块受力矢量力图和受力示意图

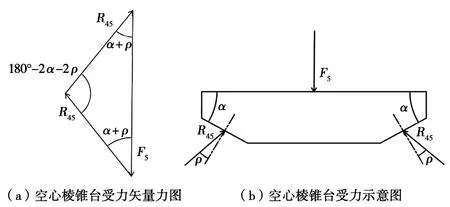
R45.楔块对空心棱锥台的总反力；F5.空心棱锥台受到的来自空心压块的作用于空心棱锥台的驱动力。图4 空心棱锥台受力矢量力图和受力示意图

由图2～图4可以得到各力与楔块给TPEE组件顶层隔片的驱动力F4之间的关系，这里F3=F4，关系式如下：

F5=K5F4

(1)

f45=Kf45F4

(2)

N45=f56ctgρ

(3)

R45=f56sin-1ρ

(4)

f41=Kf41F4

(5)

N41=f41ctgρ

(6)

R41=f41sin-1ρ

(7)

f43=Kf43F4

(8)

N43=f43ctgρ

(9)

R43=f43sin-1ρ

(10)

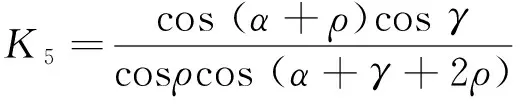
式中:f45——空心棱锥台与楔块之间的摩擦力；

N45——空心棱锥台与楔块之间的正压力；

i——单层楔形机构中楔块的个数;

f56——空心棱锥台与空心压块之间的摩擦力；

R45——空心棱锥台与楔块摩擦面间的总反力；

f41——楔块与壳体之间的摩擦力；

N41——楔块与壳体之间的正压力；

R41——楔块与壳体摩擦面间的总反力；

f43——楔块与隔片之间的摩擦力；

N43——楔块与隔片之间的正压力；

R43——楔块与隔片摩擦面间的总反力。

2.1.1.2多层楔形机构串联受力分析

多层相同楔形机构串联构成的楔形机构的受力分析可由单层楔形机构的受力分析获得。以空心棱锥台受到的驱动力F5、空心棱锥台与楔块之间摩擦力f45与楔块所受阻力F4之间关系的求解为例，设楔形机构的层数为m，第M层(顶层的)楔形机构所受驱动力为FM,5，空心棱锥台与楔块之间摩擦力为fM,45，楔块所受阻力为FM,4，第M-1层楔形机构所受驱动力为FM-1,5，空心棱锥台与楔块之间摩擦力为fM-1,45，楔块所受阻力为FM-1,4；…；第1层楔形机构(底层的)所受驱动力F1,5，空心棱锥台与楔块之间摩擦力f1,45，楔块所受阻力F1,4。

根据式(1)可推得：

(11)

根据式(2)可推得：

(12)

同理，可得：

(13)

(14)

另外，由接触面的正压力、摩擦力和总反力的关系可得：

Nm,45=fm,45ctgρ

(15)

Nm,41=fm,41ctgρ

(16)

Nm,43=fm,43ctgρ

(17)

Rm,45=fm,45sin-1ρ

(18)

Rm,41=fm,41sin-1ρ

(19)

Rm,43=fm,43sin-1ρ

(20)

2.1.2楔形机构的位移

2.1.2.1单层楔形机构位移

根据单层楔形机构位移分析可获得各元件的位移与楔块轴向位移x4之间的关系，楔块轴向位移x4与顶层隔片轴向位移x3相等，即x3=x4。这些位移包括空心棱锥台轴向位移x5、空心棱锥台与楔块之间相对位移x45、楔块与壳体之间相对位移x41；楔块与隔片之间相对位移x43。各位移与楔块轴向位移x4间的关系如下：

x4=a5x5=a45x45=a43x43=a41x41

(21)

其中：

a45=cosαctgγ

a43=ctgγ

a41=cosγ

2.1.2.2多层楔形机构串联位移

多层相同楔形机构串联构成的楔形机构位移分析可由单层楔形机构位移分析获得，以空心棱锥台轴向位移x5、空心棱锥台与楔块之间相对位移x45、楔块的轴向位移x4之间关系的求解为例，设楔形机构的层数为m。第M层(顶层的)楔形机构，空心棱锥台轴向位移为xM,5，空心棱锥台与楔块间的相对位移为xM,45，楔块的轴向位移为xM,4；第M-1层楔形机构，空心棱锥台轴向位移为xM-1,5，空心棱锥台与楔块之间的相对位移为xM-1,45，楔块的轴向位移为xM-1,4；…；第1层(底层的)楔形机构，空心棱锥台轴向位移为x1,5，空心棱锥台与楔块间的相对位移为x1,45，楔块的轴向位移为x1,4。

根据式(21)可推得,

(22)

(23)

(24)

(25)

2.2 楔形机构的功、效率、摩擦损耗率和容量

2.2.1楔形机构外部驱动力的功、效率和摩擦损耗率

根据外部驱动力作用在空心棱锥台上的功来求楔形机构的效率。当底层楔形机构的楔块所受来自TPEE元件组件顶层隔片的阻力为F1,4时，F1,4的计算公式为：

(26)

对于m层楔形机构串联而成的机构其对底层楔形机构TPEE元件所做的功E1,4的计算公式为：

(27)

外部驱动力作用在m层楔形机构串联而成的机构时第M层(顶层)的空心棱锥台上的功Em,5为：

(28)

将式(11)和式(26)代入式(28)得：

(29)

将式(22)代入式(29)可得：

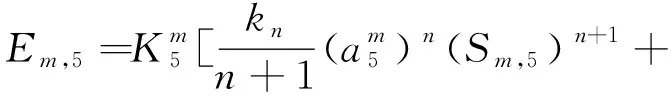
(30)

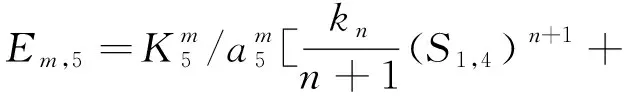
(31)

令摩擦角ρ=0°时，即无摩擦的理想状态下外部驱动力所做的功Em,50的计算公式见式(32)，此时，Em,5=Em,50，K50为ρ=0°时K5的计算结果。

(32)

将式(31)和(32)代入效率计算公式，得：

(33)

式中:ηmw——m层相同楔形机构串联构成的楔形机构的效率;

ηw——单层楔形机构的效率。

m层相同楔形机构串联构成的楔形机构的摩擦损耗率ξmw为：

ξmw=1-ηmw=1-ηwm

(34)

另外，效率还可按式(35)计算：

(35)

以上结果证明了：

(36)

Em,50=E1,4

(37)

2.2.2楔形机构的摩擦损耗、摩擦损耗率和容量

以楔形机构中的楔块与空心棱锥台之间的摩擦损耗Ef45为例，设楔形机构的层数为m，第1层(底层)楔形机构的Ef45为E1,f45；第2层楔形机构的Ef45为E2,f45；第3层楔形机构的Ef45为E3,f45；…；第M层(顶层)楔形机构的Ef45为EM,f45。

m层相同楔形机构串联而成的机构楔块与空心棱锥台之间的摩擦损耗为：

(38)

而m=M时，

这样，第M层楔形机构的楔块与空心棱锥台之间的摩擦损耗EM,f45为：

(39)

从而可推导出：

EM,f45(S1,4)=(Kf45/a45)(K5/a5)M-1E1,4

(40)

同理，可得到:

EM,f41(S1,4)=(Kf41/a41)(K5/a5)M-1E1,4

(41)

EM,f43(S1,4)=(Kf43/a43)(K5/a5)M-1E1,4

(42)

m层相同楔形机构串联而成的机构楔块与空心棱锥台之间的总摩擦损耗为：

(43)

同理可推导出Emf41、Emf43，即:

(44)

(45)

(46)

m层相同楔形机构串联构成的楔形机构的摩擦损耗为：

Emw=i(Emf45+Emf41+Emf43)

(47)

m层相同楔形机构串联构成的楔形机构的摩擦损耗率为：

(48)

m层相同楔形机构串联构成的楔形机构效率ηmw还可表达为：

(49)

根据缓冲器容量的定义可知，外部驱动力作用在顶层空心压块上的功EM,5就是其容量。底层楔块所承受的轴向力F1,4、轴向位移x1,4与TPEE弹性体组件顶层隔片的轴向力F3、位移x3分别相等。所以，F1,4与x1,4的关系可由TPEE元件缓冲器的静压试验来获得，从而，楔形机构对TPEE元件组件所做的功也可由TPEE元件缓冲器的静压试验来获得，关系式如式(50)所示：

E1,4=Ect+E1,4r

(50)

式中：Ect——TPEE元件组件的所消耗能量，可由静压试验获得；

E1,4r——TPEE元件组件的回弹的能量，可由静压试验获得。

2.3 缓冲器的能量损耗和能量吸收率

m层楔形机构串联成的楔形机构与TPEE元件组合的组合式缓冲器的能量损耗Emwt、能量吸收率ξmwt和效率ηmwt分别为：

Emwt=Emw+Ect

(51)

(52)

ηmwt=ηmwηt

(53)

式中：ηt——TPEE元件组件的能量吸收率，可由静压试验获得。

另外，ξmwt和ηmwt还可按照式(54)和式(55)计算：

ξmwt=1-ηmwt=1-ηmwηt

(54)

(55)

3 算例

以某TPEE元件缓冲器的静压试验结果为已知条件进行计算，该缓冲器行程为79 mm，最大阻抗力为2 550.096 kN，能量损耗Ect约为43.928 kJ，容量E4约为61.379 kJ，能量吸收率约为72%。

经过曲线拟合求得的缓冲器压缩过程中力F4与位移x4之间的函数关系为6次多项式，缓冲器回弹过程中力F4r与位移之间的函数关系为7次多项式，分别见式(56)和式(57)。

(56)

(57)

根据所求得的力、位移、功、能量损耗、效率和能量损耗率的计算公式，由楔形机构的关键参数α、γ和ρ便可求出楔形机构的效率和摩擦损耗率；根据TPEE元件缓冲器静压试验的关系式(式(56))和各力与第1层(底层)楔形机构楔块的轴向力F1,4之间的关系可求得所有的力；根据各元件的位移与第1层(底层)楔形机构楔块的轴向位移x1,4之间的关系可求得所有的位移；根据式(56)和式(57)可求出E1,4和E1,4r，从而根据各功、能量损耗、效率和能量损耗率与E1,4和E1,4r的关系可出求相应的功、能量损耗、效率和能量损耗率。

另外，取每层楔形机构的楔块个数i=2，取楔形机构层数m=1和m=2，也就是以单层楔形机构和两层楔形机构串联构成的楔形机构分别与TPEE元件组合成组合式缓冲器，分别给出分析结果。对于两层棱锥台楔形机构与TPEE元件组合的组合式缓冲器来说，式(56)和式(57)给出的就是底层楔形机构的楔块与顶层隔片之间的作用力。

对楔形机构进行设计计算，为节省篇幅，在此仅给出一组较优的设计方案，空心棱锥台与楔块贴合的斜平面与水平面间的夹角α=25°，楔块与壳体贴合的斜面与垂直面间的夹角γ=3°，楔形机构各摩擦面间的摩擦角为ρ=8.5°。

表1为单层楔形机构与TPEE元件组合式缓冲器的主要计算结果。

表1 单层楔形机构的组合式缓冲器静力分析主要结果

两层楔形机构的组合式缓冲器的第1层(底层)楔形机构的受力、位移、功和能量等与单层楔形机构与TPEE元件组件组合式缓冲器的相同，如表1所示；第2层(顶层)楔形机构的力比单层楔形机构与TPEE组件组合式缓冲器的楔形机构相应的力要大很多，相应的位移略有减少，功和能量消耗量都有所增加。因此，两层楔形机构的组合式缓冲器的能量消耗量、容量和能量吸收率有较大的增加，具体数值如表2所示。

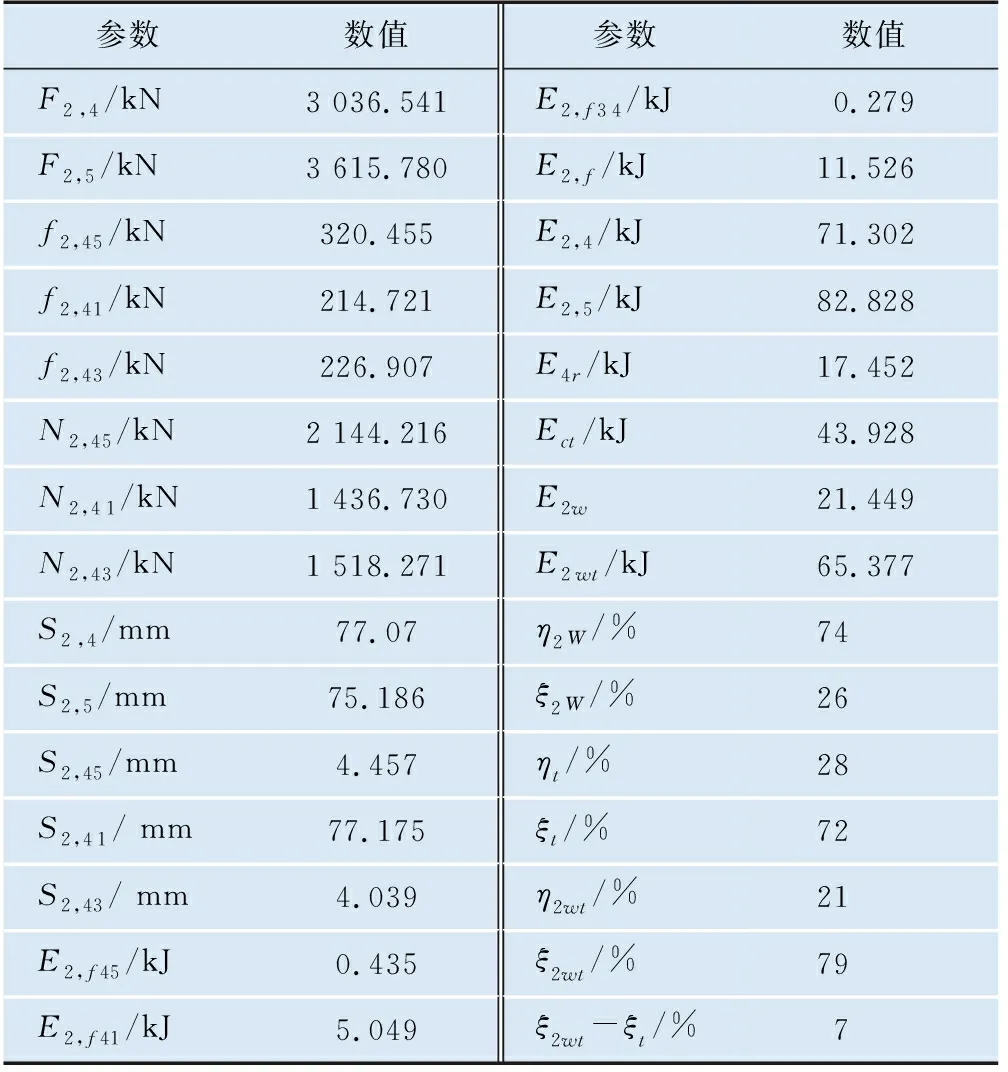
表2 两层楔形机构的组合式缓冲器静力分析主要结果

假设TPEE元件组件顶层隔片的位移一定时，楔形机构对TPEE元件组件所做的功E1,4、TPEE元件组件所吸收的能量Ect和TPEE元件组件所储存的能量E4r是不变的。对于本算例，当TPEE组件顶层的隔片的位移S1,4为79 mm时，E1,4、Ect和E4r分别为61.379 kJ、43.928 kJ和17.452 kJ。

单层楔形机构的组合式缓冲器的容量是空心压块对空心棱锥台所做的功E1,5，为71.302 kJ，摩擦损耗能量E1w为9.922 kJ；两层楔形机构的组合式缓冲器的容量是空心压块对顶层空心棱锥台所做的功E2,5，为89.529 kJ，摩擦损耗能量E2w是21.448 kJ，这是底层楔形机构的摩擦损耗能量E1,f(9.922 kJ)与顶层楔形机构的摩擦损耗能量E2,f(11.526 kJ)之和。

另外，本算例还证明了m层相同楔形机构串联构成的楔形机构的效率、摩擦损耗率和能量吸收率分别为：

(58)

(59)

(60)

相同m层楔形机构串联成的楔形机构与TPEE组合的组合式缓冲器的效率为：

(61)

以上证明了本文所给出的m层楔形机构串联成的楔形机构与TPEE组合式缓冲器的力学分析的正确性。

4 结束语

根据TPEE元件缓冲器静压试验的数据所求出的m层楔形机构串联成的楔形机构与TPEE元件组合的组合式缓冲器算例，可以得到如下结论：

(1) 本文提出的组合式缓冲器主要元件的位移、力、功和摩擦损耗以及楔形机构、缓冲器的效率和能量吸收率的计算公式是正确的。

(2) 组合式缓冲器能量收率比纯TPEE元件缓冲器的能量吸收率有明显提高。通过串联多层棱锥台楔形机构可以较大幅度地提高组合式缓冲器的容量和能量吸收率。在所研究的组合式缓冲器的具体参数条件下，单层楔形机构组合式缓冲器的能量吸收率ξ1wt为76%，比纯TPEE元件缓冲器提高了约4%；两层楔形机构的组合式缓冲器的能量吸收率ξ2wt为79%，比纯TPEE元件缓冲器提高了约7%。

(3) 由于楔块与壳体贴合面间存在γ大于0°的夹角(本例γ=3°)，使棱锥台楔形机构与TPEE元件组合式缓冲器回弹性能好于楔块与壳体贴合面间夹角γ等于0°的组合式缓冲器。

(4) 多层棱锥台楔形机构与TPEE元件组合式缓冲器和同样可提高缓冲器能量吸收率的带动板的楔形机构与TPEE元件组合式缓冲器相比，结构简单,可靠性高。