数学分析选讲课程不定积分求法的教学探究
2023-01-04王成强
王成强
(宿迁学院 文理学院, 江苏 宿迁 223800)
0 引言
为加深数学分析课程教学内容的深度,拓宽学生的数学分析视野,多数地方高校在大三或大四专门开设数学分析选讲课程以供数学专业学生选修[1,2]。除少数高校外,绝大部分高校开设的数学分析选讲课程都是数学分析课程的延续,两者教学内容相似性极高,但具体而言,数学分析选讲课程在教学内容安排上更概括,知识体系更紧凑,介绍的知识更丰富,展现的数学视野更广,蕴含的数学方法更接近前沿。数学分析选讲课程能帮助学生巩固学过的数学分析知识,夯实其数学基础,加深其对主要结果的理解认识,拓展其数学视野,提升其数学能力。
不定积分是定积分、重积分、曲线积分、曲面积分、常微分方程等理论或课程的知识与技术准备。不定积分的学习能帮助学生更深刻认识已学过的函数微分理论,培养发散的数学思维,提升数学实践能力。因此,不定积分是数学分析选讲课程的教学重点。经研究发现,不定积分也是绝大多数地属高校数学分析选讲课程的教学难点。本文旨在概要剖析地属高校数学分析选讲课程不定积分内容的教学困境,并提出突破这些困境的若干策略。
1 数学分析选讲课程不定积分教学困境分析
学生前期学习质量不高,前期课程(主要指“数学分析”课程)期末考试之后缺乏必要的复习巩固,等待修读“数学分析选讲”课程时,不少学生只剩下“学过不定积分”之印象。这致使在“数学分析选讲”课程的教学时,往往需要教师重新讲一遍基础知识,重新解释验证基本性质,重新示范基本方法与技能。正因为此,任课教师几乎不能在“数学分析选讲”课程规定的时间内完成对不定积分内容的教学任务。
在修读“数学分析”等先修课程中,学生对不定积分有关问题缺乏充分的解题训练。这致使教师在例题展示、习题答疑等环节不能宏观拟出解题思路,而必需耗费非常多时间展示解题细节。因不定积分有关问题形式多变,问题考查的侧重点有时候相去甚远,故任课教师只有提高讲解速度,才能在“数学分析选讲”课程规定的时间内完成对不定积分的教学内容。
每节课结束,教师还需要布置一定的课后习题,以帮助学生积累解题经验、复习巩固知识点、加深对教学内容的理解认识。这些补救措施压缩了真正属于“数学分析选讲”课程的教学时间,降低了“数学分析选讲”不定积分内容的教学质量。
在大学数学类课程教学中,被普遍采用的教学模式有传统的讲授式与基于MOOC等平台的线上教学模式。讲授式,即教师展示教学内容,学生聆听、模仿并进而被动吸收知识的教学模式。经过多年的亲身教学实践,教师们普遍认为,在传统“讲授式”的课堂教学中,“满堂灌”现象极其严重,缺乏必要的师生互动、缺乏个性化教学,学生无法正真理解和掌握所学知识,从而导致学生即便能机械地套公式完成练习题,也会因缺乏必要的理解和消化而丧失学习兴趣。近几年,大学数学类课程实施了线上教学实践,实现线上教学的流程大致分两类:一类是学生通过MOOC等课程平台,完成课程的学习、习题训练、期中期末测试,平台根据其监测到的学生学习数据而发放结业证书(有相应的成绩认定);另一类是,教师借助腾讯会议、微师、ZOOM、QQ软件、微信等平台,完成传统讲授式教学中的课堂教学环节,学生接受与讲授式教学完全相同的习题训练、期中期末测试。在第一类途径中,平台只能监测到学生学习课程的时长、完成作业情况、期中期末考试等,而不能对学生是否真正掌握教学内容给出准确判定;在第二类途径中,师生不能面对面交流反而加重了教师的教学负担。这些问题致使担任“数学分析选讲”课程的教师很难选择合理的教学模式。
2 数学分析选讲课程不定积分教学策略探析
2.1 择机引入探究式教学
探究式教学,即任课教师下达课堂学习任务,鼓励学生通过生与生、生与师之间的思维碰撞探索出消化、理解学习内容的路径,监督辅导学生研读文献并适时合理地进行思维干预,引导学生自主完成学习任务,从而完成教学的模式[3]。在“数学分析选讲”课程的教学中,为示范应用某种处理不定积分问题的方法,教师摒弃以往先花时间补知识点巩固基础再深入开展教学的方式,利用探究式教学,使学生亲自参与到解答问题的过程中,主动地、循序渐进地了解并掌握解题理论或方法。
求有理函数的不定积分综合难度极高,其过程“冗长”且需要应用多种不定积分问题处理技巧,因此,该部分内容一直都是数学分析选讲课程的教学难点。笔者曾以例1为学习素材,开展探究式教学,引导学生通过解题实践掌握了求有理函数不定积分的一套高效方法。

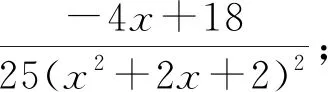
学生已经完成了诸如“复习基于部分分式分解的有理函数不定积分的求法”等准备任务,故经教师引导,学生想到将被积函数作下述分解,
其中,Ak(k,=1,2,…,7)满足下述非齐次线性代数方程组,
经笔者进一步引导,学生对上述线性方程组的增广矩阵实施初等行变换并得到,

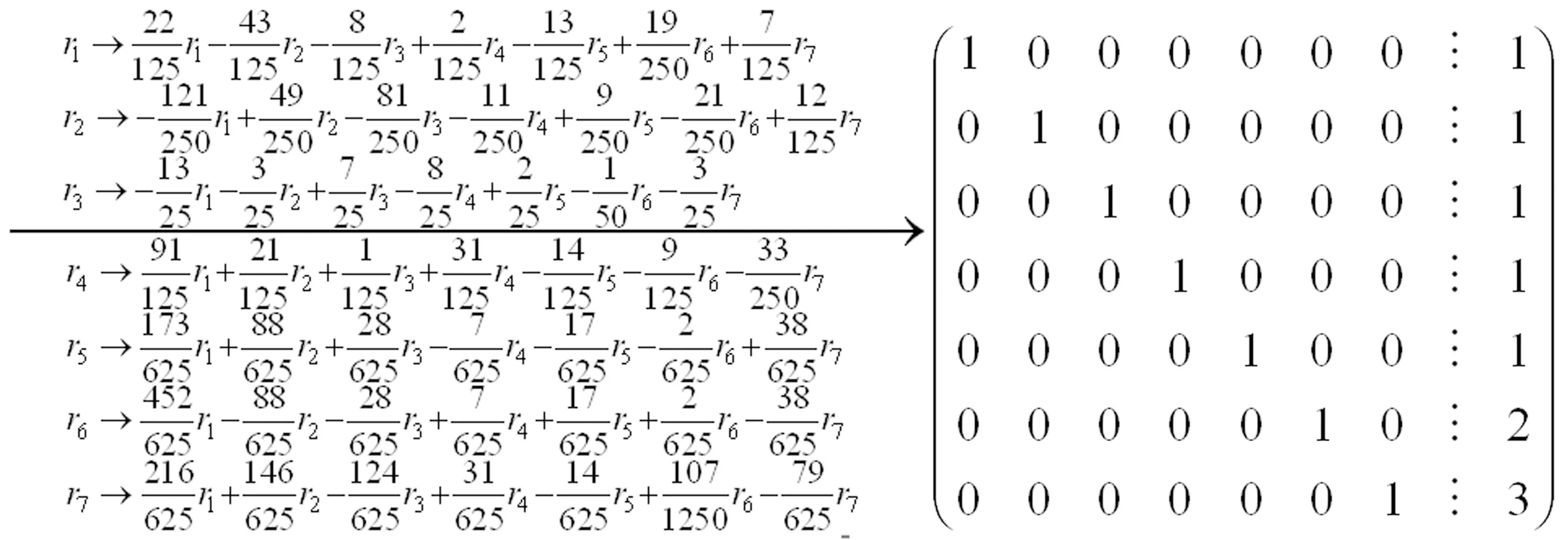
至此学生便能自动得到A1=A2=A3=A4=A5=1,A7=2且A7=3。最后,学生都独立完成了其余步骤:
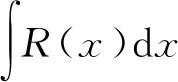
经探究式教学,学生通过亲身演算,自己发现了例1的一种“新”解答,并在解题经验基础之上,由教师有意识地引导,总结出了处理有理函数不定积分问题的一套方法(Hurwitz-Ostrogradskii方法):化被积函数为既约真分式→将不定积分分解成有理部分和无理部分(初等超越函数)之和,而且学生还能从推导过程中意识到:借助基于部分分式分解的有理函数不定积分的计算方法可证明Hurwitz-Ostrogradskii方法对有理函数不定积分的计算总是有效的。与这里处理方法类似,笔者还借助探究式教学完成了分部积分法、换元积分法等不定积分相关内容的教学任务。实践表明,探究式教学能让教师“多快好省”地完成很多不定积分内容的教学。笔者发现,适时引入探究式教学,学生能在课前能复习巩固好旧知识,并能在一定程度上完成学习新知识的任务,这就能让教师有效避开为复习旧知识而再完整呈现学生本该掌握的数学分析课程中不定积分内容的教学困境。
2.2 择机引入一题多解教学
一题多解教学,即教师引导学生从不同视角出发,发现同一道问题的多种不同解法的教学模式[4]。在数学分析选讲课程中学习不定积分时,学生对知识的掌握不牢靠,总有“哪种不定积分问题适合哪套方法”的疑惑。通过一题多解教学,能帮助认识到很多不定积分问题本身就适合于多种处理方法。例如,很多数学分析(选讲)教材中都含有下述问题:
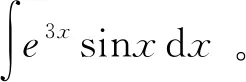
经教师引导,绝大部分学生能回忆起书本对例2的处理方法,即解法1。
解法教学1先采用两次分部积分,再解方程便能完成的解答。因绝大多教材都呈现了此种解法,经过基本训练的学生也能顺利完成解答任务,此处略去解答过程细节。
解法教学2引导学生借助Leibniz法则,得到

解法教学3引导学生借助复数的运算性质,得到下述解法:

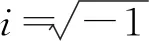
解法教学4引导学生直接套用笔者曾经介绍过的一个公式:对任何不全为零的实数a与b有

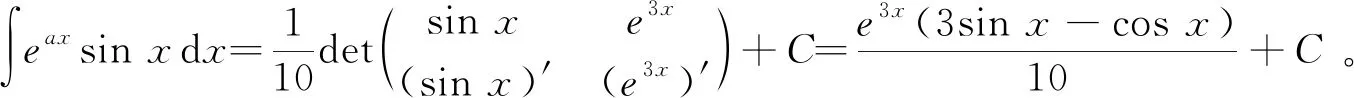
解法教学5引导学生经计算得到下述关于e3xsinx、e3xcosx的线性方程组
唤起学生对Cramer法则的记忆,并套用该法则得到:
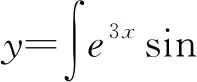
y′=e3x((3A+B)cosx+(-A+3B)sinx)=e3xsinx
一题多解,能帮助学生养成用运动发展的观点看问题,用批判发散的思维理解认识问题,创造地运用知识处理问题等良好习惯[4]。在“数学分析选讲”课程不定积分的教学中,笔者还多次借助一题多解教学完成了分部积分法、换元积分法等不定积分相关内容的教学任务。
2.3 全程采用基于SPOC理念的线上线下混合教学模式
线上线下混合教学模式,综合了传统的线下教学与新兴的线上教学两种模式的优点[5]。基于SPOC (Small Private Online Course,小规模限制性在线课程)理念,教师把与数学分析选讲课程中的不定积分教学内容剖分成若干学习模块,向学生发布学习任务与针对性的习题,学生在课前自主完成学习与解题训练任务,在课中教师解答学生学习中的疑问,择机应用探究式教学、一题多解教学等手段完成不定积分的教学任务,教师在师生互动中感知学生哪些部分的学习未达标,并在课后的教学反思环节中,修改下节课的教学任务。“数学分析选讲”课程中不定积分基于SPOC理念的线上线下混合教学模式可简要概括成图1,从该图中可看出,教师在整个教学中都起着关键作用。在学生完成对不定积分的学习时,教师需要对学生的学习表现作出评价;评价结论最后要在期末成绩中体现。教学实践数据表明,在探究式教学、一题多解教学等辅助下,采用基于SPOC理念的线上线下混合教学模式开展教学,既能高效高质量完成该部分的教学任务,还能极大限度顾及到个性化发展,与此同时,学生的学习主动性显著增强,综合运用不定积分相关的理论与方法的能力显著提升。
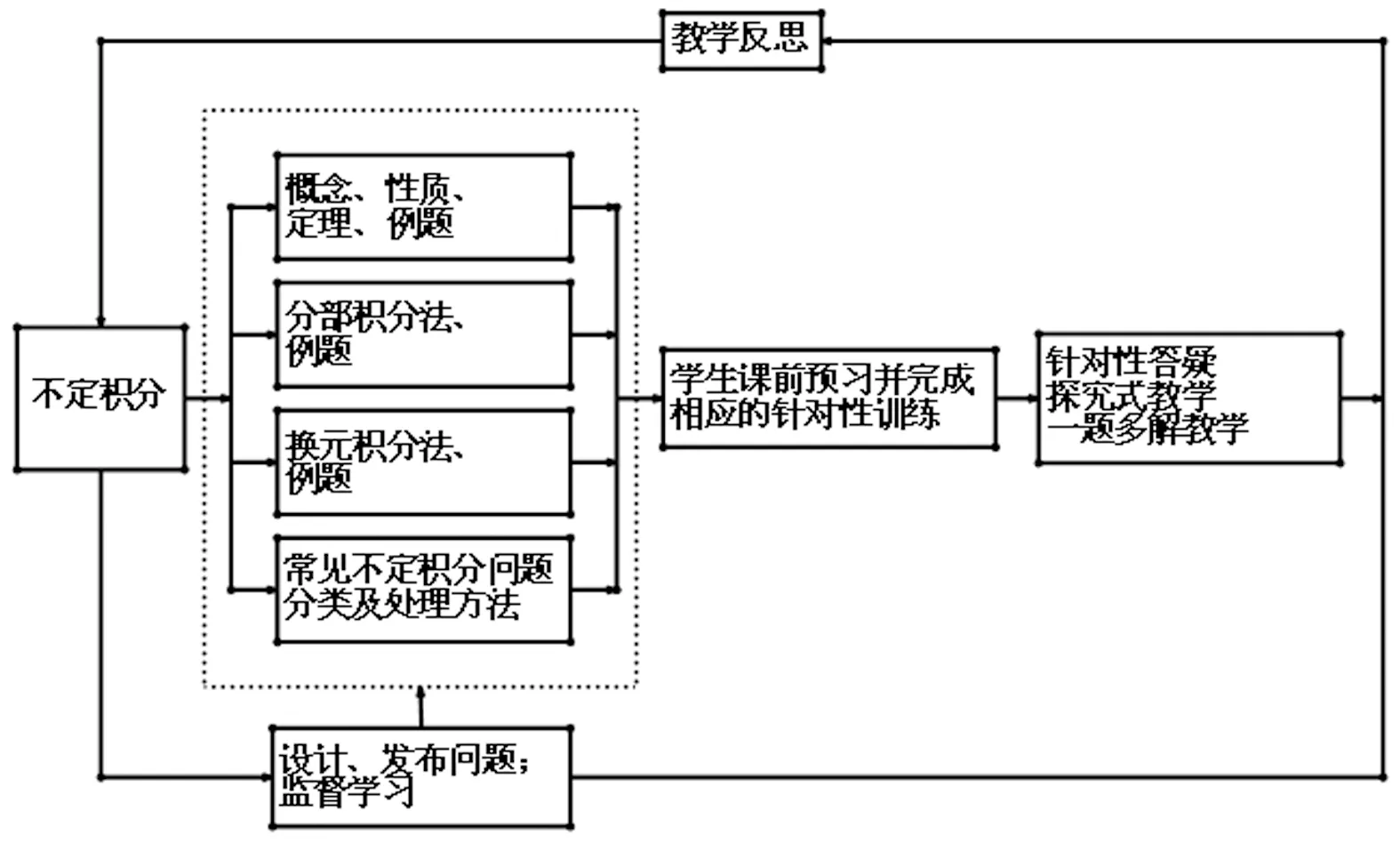
图1 数学分析选讲课程中不定积分线上线下混合教学模式流程图
3 结束语
实践证明采用基于SPOC理念的线上线下混合教学模式,引入探究式教学、一题多解教学等手段可以有效解决高校“数学分析选讲”课程不定积分内容的教学困境。
