高速列车制动风翼板不同迎风角气动性能影响分析

谢红太

（1华设设计集团股份有限公司 铁道规划设计研究院，南京 210014；2兰州交通大学 机电工程学院，兰州 730070）

高速列车风阻制动系统的制动风翼板形状、迎风角度及安装位置的选择确定，直接关系着整车制动效率及行车安全。高立强、奚鹰及MinKyo Lee等人［1-3］初步研究显示，在高速列车制动风翼板纵向投影面积相同的条件下，所产生的空气制动力依次为凹板型大于平板型，平板型大于凸板型结构。由此可见，在制动风翼板纵向投影面积相同的情况下，风翼板展开迎风面积、安装角度、表面形状及局部细节结构也是直接影响空气制动效果的主要因素。文中选用平板型制动风翼板为研究对象，以制动风翼板安装迎风角度为主要研究参数，计算分析不同工况下带制动风翼板高速列车气动性能。

1 计算模型创建

结合现有研究技术成果，文中研究采用目前常见平板型风翼板，宽高为l×hʹ的长方形结构［1，4-5］，厚度为40 mm，与车顶面呈迎风角γ横向对称布置，如图1所示。根据Davis公式列车总阻力为式（1）：

图1 制动风翼结构参数

式中：A+(B1+B2)V为列车机械阻力；C1V2为列车外部气动阻力，即列车所受的气动阻力与速度平方成正比。

基于三维定常不可压的黏性流场N-S及k-ε双方程模型［6-8］，采用计算流体动力学方法对其所产生的制动力及气动效应做初步研究。计算高速列车流体动力学模型创建具体参照文献［9-11］中相关内容，整车计算几何模型采用3辆编组1∶1实车模型，进行网格划分并设定边界条件。

制动风翼板选用整体长方形板型结构，非制动状态时，风翼板内嵌于列车顶面下陷凹槽中［12-13］；高速制动时，升起风翼板凹槽补偿机构进行填补，可有效改善车顶表面流场结构，大大削弱风阻制动噪声，因此风翼板周围车体表面按光滑表面考虑。

带有单排制动风翼的高速列车（风翼板计算算例参数：速度350 km/h，首排制动风翼板设置位置距离头车车身与司机室流线型连接处500 mm，风翼板迎风角为45°）在模拟流场中横向力FS、垂向力FL及纵向力FD受力迭代收敛计算目标曲线，如图2所示。其中，理想条件下由于外流场结构设置横向对称边界条件，横向力FS受力目标迭代计算曲线随着迭代计算逐步完成，逐渐趋近于0，垂向力FL及纵向力FD分别逐渐趋近于一个稳定值。

图2 列车受力目标迭代计算曲线

2 计算分析

2.1 气动特性分析计算

文中模拟风速为350 km/h，于高速列车头车设置单排制动风翼板，首排制动风翼板设置位置距离头车车身与司机室流线型连接处D0点500 mm，对制动风翼板迎风角γi=45°、50°、60°、70°、80°、90°（i=1，2…6）分别进行数值模拟计算。

高速列车所受空气阻力FD、垂向升力FL及横向力FS分别为式（2）～式（4）：

式中：C1，C2，C3分别为计算空气阻力系数、计算升力系数、计算横向力系数，分别写为式（5）～式（7）：

高速列车滚转力矩Mx、俯仰力矩My及偏航力矩Mz分别为式（8）～式（10）：

式（2）～（10）中：V为静止风环境中列车运行速度；AD为迎风面积，即列车纵向投影面积，m2（文中制动风翼板纵向投影面积S0=0.956 m2，不带制动风翼板列车纵向投影面积S=10.863 m2，迎风面积AD=S+S0=11.819 m2）；AL为 列 车 垂 向 投 影 面积，m2（垂向投影面积AL=274.059 m2）；ρ为空气密度，kg/m3，根据计算模型热动力参数（热动力参数：P=101.325 kPa，T=293.2 K），取ρ=1.205 kg/m3；AS为列车横向投影面积，m2；CD为阻力系数；CL为升力系数；Cmx为滚转力矩系数；Cmy为俯仰力矩系数；Cmz为偏航力矩系数；lij各方向力的力臂，m。

结合式（5）～式（7）列车空气阻力与列车纵向投影面积AD成正比，为使各研究方案具有可比对性，文中在针对制动风翼板不同安装迎风角度的方案研究中，设定列车纵向迎风面积相同，均为S0=0.956 m2，则安装迎风角度γi对应制动风翼板迎风面面积

设定目标参数，模拟列车在长大明线上运行，对列车所受纵向空气阻力FD、垂向升力FL及横向力FS进行流体动力学仿真计算。理想条件下，列车横向力FS=0，滚转力矩Mx=0，偏航力矩Mz=0，对应的横向力系数CS=0、滚转力矩系数Cmx=0，偏航力矩系数Cmz=0。

当模拟风速为350 km/h，不同迎风角γi对应高速列车所受空气阻力FD、垂向升力FL及俯仰力矩My分别如图3～图5所示。

图5 迎风角γi—俯仰力矩曲线

由图3、图4可以看出，随着迎风角γi的增大，列车所受空气阻力整体趋于平稳，所受垂向升力随着迎风角γi的增大，呈逐渐上升趋势。γi在45°～90°范围内，列车空气阻力系数CD约为0.24左右，列车升力 系 数CL约在1.4×10-3～2.0×10-3范围内。

图3 迎风角γi—空气阻力曲线

图4 迎风角γi—垂向升力曲线

不带制动风翼板高速列车模型以速度350 km/h运行时，所受俯仰力矩M0=543.19 kN·m。如图5所示，制动风翼板迎风角γi在45°～90°范围内，随着迎风角的增大所受俯仰力矩My呈先增大后减小再缓慢增大的趋势，曲线前后分布在不带制动风翼板所受俯仰力矩M0点的上下两侧。因此俯仰力矩可作为高速列车制动风翼板迎风角角度参数优化的一个重要量化指标，其反映出高速列车的点头振动程度。

经模拟计算，带不同大小迎风角制动风翼板列车在不同速度等级运行情况下对应的空气阻力FD及垂向升力FL分别如图6、图7所示。

图6 列车速度—空气阻力拟合曲线

图7 列车速度—升力拟合曲线

由图6、7可知，带不同迎风角γi的制动风翼板列车所受空气阻力FD和垂向升力FL随运行速度的增加均呈现出二次抛物线形状趋势。所受空气阻力FD随着迎风角γi的增大基本维持不变，所受垂向升力FL随着迎风角γi的增大而缓慢增加。不同迎风角γi对应列车阻力系数、升力系数、计算阻力系数及计算升力系数值见表1。

表1 不同迎风角γi列车气动特性系数值

其中，制动风翼板迎风角γi=45°、60°、80°、90°（i=1，3，5，6）时，列车纵向对称面上流场压力分布和速度分布分别如图8、图9所示。

从图8不同迎风角γi列车纵向对称面上流场压力分布可以看出，随着迎风角γi的逐渐增大，制动风翼板前后形成的正压区与负压区影响范围逐渐变小减弱，当γi=90°时，风翼板前后形成的正负压区，减到相对最弱。由图9可知，随着迎风角γi从45°～90°范围内逐渐扩大，制动风翼板背部气流干扰效应逐渐减弱。

图8 不同迎风角γi列车纵向对称面上流场压力分布

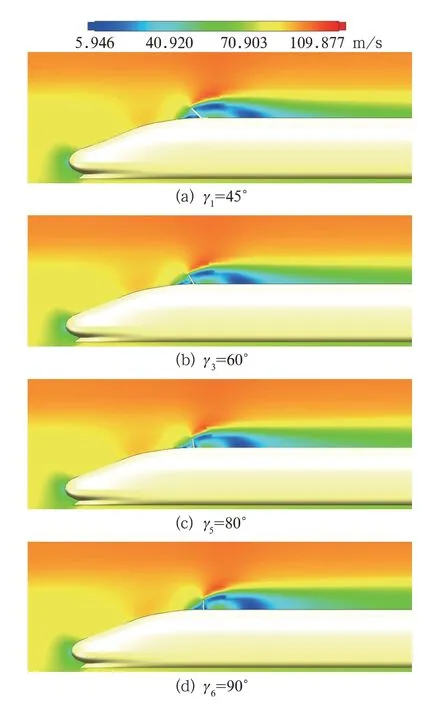
图9 不同迎风角γi列车纵向对称面上流场速度分布

2.2 风翼板特性分析

不同迎风角γi制动风翼板迎风面所受空气压力如图10所示，可知迎风面所受空气最大压力从γi=45°开始逐渐增大，到约50°时受压达到最大，而后呈逐渐下降趋势，最小压力与之相反，平均压力基本保持平稳。

图10 不同迎风角风翼板迎风面压力

分别以不同风速模拟高速列车各速度运行等级，通过计算流体动力学仿真分析，经拟合计算制动风翼板迎风面不同迎风角δi对应的计算最大压力系数Cmax，计算最小压力系数Cmin，计算平均压力系数Cave分别见表2。

表2 不同迎风角γi制动风翼板迎风面最大、最小及平均压力系数

其中制动风翼板迎风角γi=45°、60°、80°、90°（i=1，3，5，6）时，风翼板迎风面表面所受空气压力分布如图11所示。整体上对于制动风翼板不同安装γi，对应迎风面所受空气压力基本呈上下2个高正压区（分别记为第一高压区与第二高压区），左右两侧负压带的分布形式；其中，当γi=45°时制动风翼板迎风面相对受压达到最大，同时第二高压区受压峰值凸出，随着迎风角γi的逐步增大，第二高压区受压峰值逐渐减小，同时逐渐与第一高压区上下缩减分离。

图11 不同迎风角γi风翼板迎风面压力分布

制动风翼板不同迎风角γi对应风翼板迎风面所受纵向力及垂向力主要受制动风翼板对应方向投影面积影响较大，如图12所示，在风翼板迎风面纵向投影面积保持不变的情况下，纵向分力平均为2 623 N，整体随着γi的增大略有增大；随着迎风角γi的逐步增大，制动风翼板在垂向投影面积逐渐减小，对应所受垂向力逐渐减小，当γ6=90°时为0。

图12 不同迎风角γi风翼板迎风面所受分力

经流体动力学仿真计算，带单排制动风翼板高速列车以速度350 km/h运行时，如图13所示，制动风翼板迎风角γi对应的风翼板迎风面声学能量在80～95 dB的区间范围内随着γi的逐步增大表现出先增大后减小的变化趋势。

图13 不同迎风角γi风翼板迎风面声学能量等级

2.3 列车纵向对称面流场分析

参考文献［9］分别提取带制动风翼板列车纵向对称面上部外流场与列车截面接触线，如图14所示。

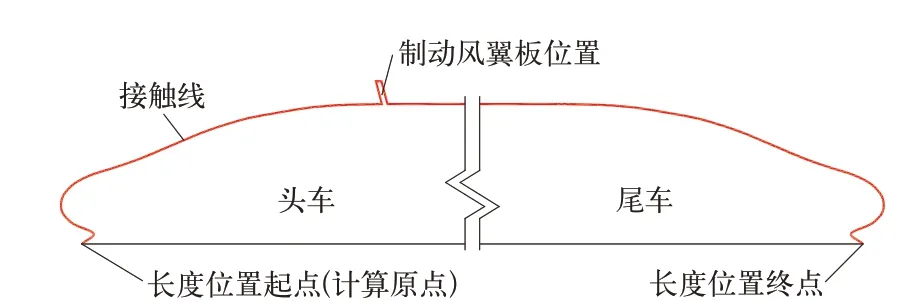
图14 列车纵向对称面接触线提取示意图

经迭代计算，高速列车纵向对称面流体与列车表面接触线长度方向上空气热动力参数曲线分别如图15、图16所示。列车鼻尖处与风翼板迎风面正压区的空气流场密度大于计算模型流场远环境空气密度（ρ=1.205 kg/m3），风翼板背风面至尾车排障板下底部点由于流体分离，空气密度值均小于远环境空气密度。空气温度在制动风翼板前后波动较大，中间车车顶部分基本保持一致，尾部列车鼻尖区域流体温度略有增大。

图15 列车纵向对称面上部接触线空气密度曲线

图16 列车纵向对称面上部接触线空气温度曲线

依次计算从头车至尾车接触线长度位置—压力分布，如图17所示，列车纵向对称面接触线上压力分布依次在高速列车导流罩范围、头车及尾车车身与司机室流线型连接范围、制动风翼板安装范围呈现正、负压力突变。列车前缘鼻部滞止点至后司机室上部，随着表面空气流动速度逐渐增大，出现第一负压区，与不带制动风翼板列车计算模型相比，该负压区影响范围表现出大幅减弱同时有前移趋势；在制动风翼板前后区域由于气流的压缩和分离，分别形成2个压差较大的正压区和负压区，在风翼板后部的列车中部车体表面，气动压力分布较为平稳，列车尾部由于流体逐渐分离形成第二负压区，该负压区相对不带制动风翼板列车计算模型有所减弱。

图17 列车纵向对称面上部接触线压力曲线

结合非稳态的N-S方程，高速列车气动噪声普遍采用FW-H方程［14-18］，经流体仿真模拟计算，在列车纵向对称面上部列车与空气流固接触线上，随长度位置点变化，声功率及声学能量等级曲线分别如图18、图19所示。

图18 列车纵向对称面上部接触线声功率曲线

图19 列车纵向对称面上部接触线声学能量等级曲线

由图18可知，列车纵向对称面上部列车与空气流固接触线上声功率值在制动风翼板迎风面背风面区域有突增，约0.001 52 W/m3，最大峰值出现在制动风翼板上部边缘处，约为0.013 93 W/m3。声学能量等级值在制动风翼板前后波动最大，前后5 m范围内大于60 dB，随后在中间车车顶逐渐减小，在列车尾部随着流体分离略有增大。

3 结论

（1）随着首排制动风翼板迎风角在45°～90°的范围内逐渐扩大，列车所受的空气阻力基本保持不变，列车空气阻力系数CD约为0.24左右，所受垂向升力呈缓增的趋势，列车升力系数CL约在1.4×10-3～2.0×10-3范围内，气动干扰效应及风翼板迎风面高压区受压逐步减弱。

（2）针对制动风翼板不同安装迎风角度，迎风面所受空气压力基本呈上下2个高正压区、左右两侧负压带的分布形式，随着迎风角在45°～90°范围内逐渐扩大，第二高压区受压逐渐减弱，同时逐渐与第一高压区上下缩减分离。

（3）列车纵向对称面接触线上压力分布依次在高速列车导流罩范围、头车及尾车车身与司机室流线型连接范围、制动风翼板安装范围呈现正、负压力突变。其中，列车前缘鼻部滞止点至后司机室上部，随着表面空气流动速度逐渐增大，出现第一负压区，与不带制动风翼板列车计算模型相比，该负压区影响范围表现出大幅减弱同时有前移趋势；在制动风翼板前后区域由于气流的压缩和分离分别形成2个压差较大的正压区和负压区，在风翼板后部的列车中部车体表面，气动压力分布较为平稳，列车尾部由于流体逐渐分离形成第二负压区，该负压区压力相对不带制动风翼板列车计算模型有所减弱。

（4）列车纵向对称面上部列车与空气流固接触线上声功率值在制动风翼板迎风面背风面区域有突增，约0.001 52 W/m3，最大峰值出现在制动风翼板上部边缘处，约为0.013 93 W/m3。声学能量等级值在制动风翼板前后波动最大，前后5 m范围内大于60 dB，随后在中间车车顶逐渐减小，在列车尾部随着流体分离略有增大。