高速列车轴箱轴承保持架动态特性研究*

2023-01-04涂文兵陈超项云鹏

铁道机车车辆 2022年6期

涂文兵，陈超，项云鹏

（华东交通大学机电与车辆工程学院，南昌 330013）

轴箱作为高速列车重要传动部件之一，在实现列车轮对与构架间相互连接、相互运动中发挥至关重要的作用［1］。轴箱轴承工作状态的好坏会直接影响列车运行的平稳性、安全性和可靠性。保持架是轴承的一个关键元件。随着列车运行速度的增加以及频繁的加减速，保持架与滚动体之间的相互运动和作用力变得更加复杂，且较大的碰撞力会影响保持架的运动稳定性，也会加剧保持架的磨损和损坏，而保持架的动态性能对于整个轴承工作性能有着至关重要的影响。因此，研究高速列车轴箱轴承保持架的动态特性对于轴承使用寿命、保持架设计等具有重要的理论指导意义和实际参考价值。

近年来国内外研究人员对保持架动态特性展开了大量的研究。Walters建立了球轴承的保持架六自由度动力学分析模型，开创性地研究了保持架的动态性能［2］。刘秀海等建立了圆柱滚子轴承保持架三自由度动力学分析模型，对比分析了径向力、内圈转速以及轴承游隙等参数对保持架动态特性的影响［3］。Chen等研究了保持架引导方式和油膜厚度对保持架稳定性的影响，得到了不同引导方式和旋转方式下的保持架质心运动轨迹［4］。Pederson等研究了深沟球轴承柔性保持架与刚性保持架的动态性能，结果表明刚性保持架与球的碰撞力要大于柔性保持架与球的碰撞力［5］。邓四二等分析了角接触球轴承考虑柔性保持架的运动稳定性，结果表明柔性保持架比刚性保持架运行更加稳定［6］。孙雪等对比分析了载荷和转速分别在柔性和刚性套圈下保持架运动稳定性的影响［7］。姚廷强等建立了考虑轴承弹性变形的角接触轴承有限元模型，研究了径向力、引导游隙和转速对保持架运动稳定性的影响［8］。黄运生等以轴箱轴承为研究对象，在对保持架进行离散化处理的基础上进行柔性建模，将车轮扁疤对轴承产生的冲击作为载荷激励，研究了冲击载荷对铁路轴承塑料保持架运动特性的影响［9］。吴正海等研究了考虑脂润滑对保持架的作用下，不同径向力、内圈转速、轴承预紧量以及保持架自身材料特性等参数对保持架动态特性的影响［10］。范然然等探究了考虑油膜等效接触刚度情况下，引导间隙、兜孔间隙和引导方式等对保持架动态性能的影响［11］。邓四二等对比研究了保持架不同引导方式对其运动稳定性的影响［12］。涂文兵等分析了轴承在减速工况下受到的轴向载荷、径向载荷以及减速度对保持架动态性能的影响［13］。上述文献分析了刚性或者局部柔性情况下滚动轴承在不同转速、载荷、轴承自身形状参数以及保持架引导方式不同情况下保持架的动态运动特性，而多数文献把滚动轴承各元件视为刚体，分析工况主要集中在稳定工况。考虑轴承柔性接触和非稳定工况下的保持架动态性能的研究较少，特别是在高铁轴承方面。

因此，文中建立了高速列车轴箱轴承柔性多体动力学有限元仿真模型，利用ANSYS/LS-DYNA模块对有限元模型进行计算求解，研究在不同车速和减速度工况下轴箱圆柱滚子轴承保持架的动态特性。

1 有限元模型的建立

1.1 轴承几何参数

轴箱轴承主要功能是将来自车体的重量和载荷传递给轮对，轴承内圈与车轴过盈配合，外圈通过过盈配合固定在轴承座上。文中以某高速列车轴箱双列圆柱滚子轴承为研究对象，建立了二维有限元模型，如图1所示。模型主要参数见表1。y方向的平动自由度。与单线性位移、常应力应变的三角形网格相比，四边形网格划分形状规整，网格划分便捷且其位移、应力与应变呈线性变化，故平面模型一般优先选择四边形网格。为提高模型计算精度，根据轴箱轴承的形状、尺寸对轴承进行针对性网格划分。模型网格设置如下：滚子圆周和内部划分成四边形网格，局部过渡区域划分为三角形，其余零部件划分采用四边形网格，划分结果如图2所示。

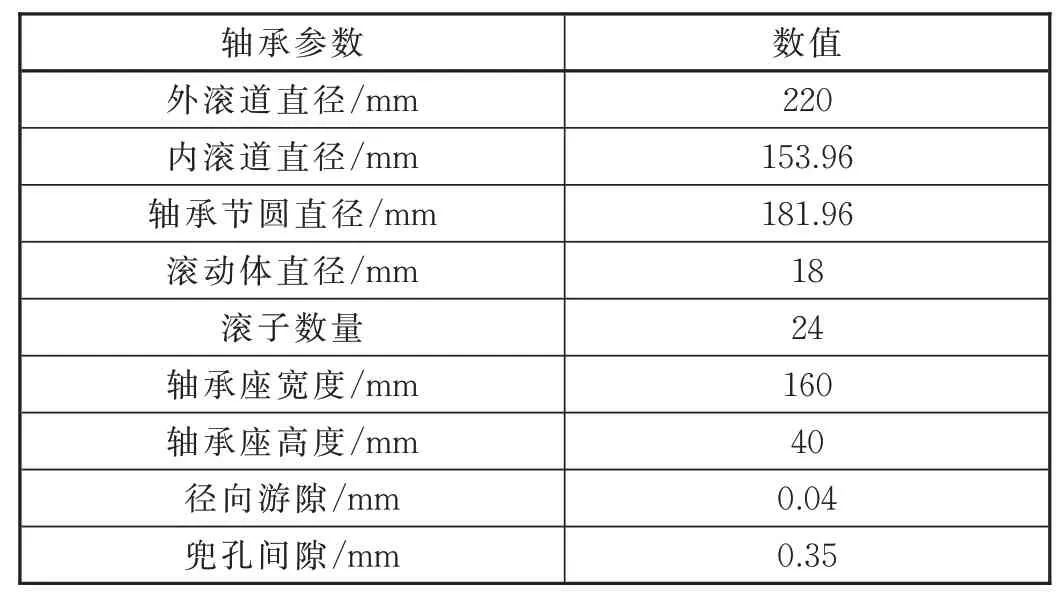
表1 轴承主要参数

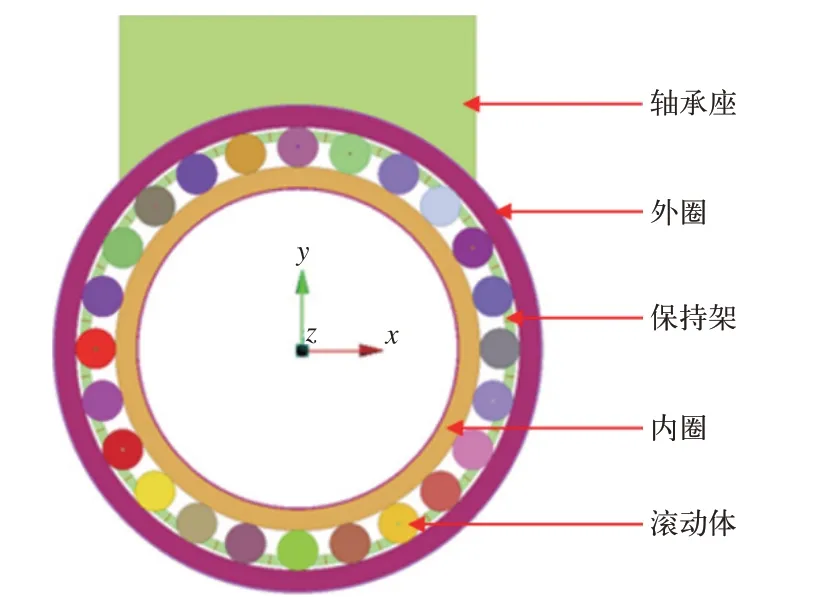
图1 有限元模型

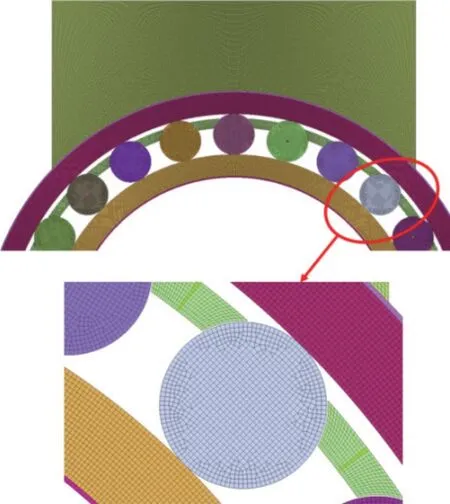
图2 轴承及轴承座有限元模型

轴箱轴承为双列，因此，在保证计算精度的前提下，为提高计算效率，文中对单列轴承进行分析，建立如图1所示有限元模型，并将模型导入ANSA软件中进行网格划分和参数设置。

1.2 网格划分

文中建立的是二维有限元模型，为保证模型计算的精度和准确性，选用SHELL163单元划分网格。考虑到滚动轴承内部元件局部接触变形，因此，设置网格单元为平面应变单元。SHELL163中的每个单元有4个节点，且每个节点都只留下x和

轴箱轴承以及轴承座的塑性变形较小，因此，将模型的材料设置为线弹性材料。采用钢制材料设置其密度ρ=7 850 kg/m3、弹性模量E=200 GPa、泊松比μ=0.3。

1.3 接触设置

与点—面接触相比，面—面接触更适用于处理物体之间有大量滑动和形变刚度较大的问题。因此，本模型的接触设置为二维自动面-面接触，并且忽略由润滑、摩擦等引起的摩擦因数衰减系数。根据轴箱轴承的实际接触情况，总共为模型设置了73对接触。其中：1对外圈与轴承座接触、24对滚子与外圈接触、24对滚子与保持架接触、24对滚子与内圈接触，轴承各元件间的动摩擦系数设置为0.005，静摩擦系数设置为0.05；同时，为避免外圈与轴承座之间发生相对滑动现象，外圈与轴承座间选取较大的摩擦系数，静摩擦和动摩擦系数分别设置为0.1和0.01。

1.4 约束与载荷的施加

在轴箱轴承实际工作中，为避免蠕滑，通常采用过盈配合的方式连接轴承内圈与轴以及外圈与轴承座，且内圈—车轴、外圈—轴承座间近似于刚性连接，因此，为防止仿真时内外圈和轴承座不会被冲散开同时便于载荷的施加，在外圈外缘以及内圈内缘圆周上各添加一圈网格并设置为刚体单元。在内圈添加的刚体单元上施加x、y方向的位移约束以限制内圈的移动自由度，使内圈只留下平面转动自由度。为约束轴承座在x方向的运动，在轴承座最上方的节点上施加x方向的位移约束，使轴承座只留下y方向移动自由度。为了模拟保持架真实的运动情况，保持架不施加任何约束。

目前，高速列车的试验运行速度已经突破600 km/h，文中分别选取了列车在150、250、350、450 km/h这4种不同速度工况下轴箱轴承保持架动态特性的变化规律，在研究车速对保持架动态性能的影响时，分别在轴承内圈内侧刚性壳单元上对应施加90.579、150.966、211.353、271.739 rad/s的转速；在研究减速度对保持架动态性能的影响时，在内圈内侧添加的刚性壳单元上施加初始转速为180 rad/s，减速度分别为45、90、135、180 rad/s2。查阅资料发现某型高速列车车身质量约为11 t，由于建模过程中只考虑了单列圆柱滚子轴承，因此在轴承座最上方施加沿y负方向大小为27 500 N的载荷。在显式动力学分析模型时，由于施加的载荷和转速都是关于时间的函数，为了避免突然施加较大的载荷与转速造成轴承运转的失稳，分别设置载荷和转速时程曲线经0.01 s后由0线性增加至稳定值。

2 结果分析与讨论

2.1 模型验证

为验证模型的有效性，将所建立的有限元模型导入到ANSYS/LS-DYNA模块中进行计算，提取计算结果中保持架平均转速和承载区滚子的平均自转转速的仿真解，并与文献［14］中理论计算公式计算的解析解进行对比验证，其中理论公式为式（1）～式（3）：

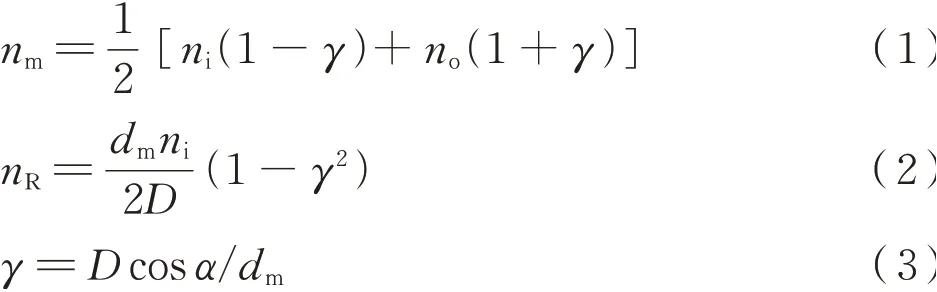
式中：nm、nR分别为保持架公转转速和滚子自转转速；ni、no分别为轴承内、外圈转速；D为滚子直径；dm为轴承节圆直径；α为轴承初始接触角。

仿真解与解析解对比结果见表2。从表2中分析可以明显看出，保持架公转转速和滚动体自转转速的仿真解与解析解总体上较为一致，吻合效果较好且误差均不超过1%，从而验证了文中所建有限元模型的有效性。

表2 仿真解与解析解对比表

2.2 稳定工况下保持架动态性能分析

保持架打滑动态特性可以通过保持架的打滑率定量分析，保持架打滑率定义为保持架理论转速与实际转速的相对误差，其公式可表示为式（4）：

式中：ω0为理论转速；ω为保持架实际转速。

不同车速下保持架打滑率如图3所示。通过图3分析可知，匀速工况下，保持架的打滑率在0附近波动，且随着车速的增加，打滑率波动幅度逐渐减小。这是由于轴箱轴承处于低速重载工况下，轴承整体打滑效应较弱；随着列车运行速度的提高，滚子的离心效应也随之得到强化，在离心力的作用下使滚子更加压紧轴承外圈内滚道运动，此时，滚子与保持架兜孔间的碰撞力的变化逐渐减小，保持架运动更加趋向于稳定，其打滑率的波动幅度随着内圈转速的增加而减小。

图3 不同车速工况下保持架打滑率

通过观察保持架质心轨迹可以定性分析保持架的运动稳定性。当质心轨迹相对集中时，保持架主要绕其惯性坐标系坐标原点转动，此时保持架的运动比较稳定；当质心发生涡动时，则需要根据涡动速度、形状等来评判稳定性。保持架质心速度偏差比值通常用来评判运行稳定性，且其值的大小与保持架运行稳定性成负相关性，该指标评估法被称为Ghaisas［15］法，其计算公式为式（5）：

式中：σv为速度偏差比；vi为保持架质心的瞬时速度；vˉ为保持架质心的平均速度。

不同车速工况下保持架质心轨迹和质心速度偏差比如图4、图5所示。通过图4、图5分析可知，随着车速的提高，轴箱轴承保持架质心运动轨迹逐渐趋于集中且σv值逐渐减小，说明随车速的提高，保持架的稳定性得到提高。车速的提高导致滚动体自身离心效应增大，滚动体更压紧外滚道运动。在外滚道的约束下，滚动体的运动平稳性增强，滚子与兜孔间碰撞接触力的波动程度减小，进而导致保持架的质心速度偏差比减小、保持架运行稳定性增强。

图4 不同车速工况下保持架质心运动轨迹

图5 不同车速工况下保持架质心速度偏差比

2.3 减速度工况下保持架动态特性分析

不同减速度工况下保持架公转转速时程曲线如图6所示。通过图6分析可知，减速度工况下，保持架的公转转速随时间的加长逐渐减小，且减速度越大，保持架转速减小得越快。

图6 减速度工况下保持架转速

保持架平均打滑率随减速度变化曲线如图7所示。由图7分析可知，匀速工况下，保持架的平均打滑率大于0.5%；减速度为45 rad/s2时，保持架的平均打滑率小于0，呈现负打滑趋势，且保持架平均打滑率的大小随着减速度的增大近似呈线性变化。当轴承匀速转动时，存在一定的阻力约束滚子和保持架的运动，使得轴承的整体打滑效应较弱，导致保持架的平均打滑率比其理论值略小，此时保持架表现出正打滑状态；而减速工况下，当内圈以一定的减速度运动时，滚子与保持架的惯性使得内圈转速的变化超前于保持架，此时保持架的实际转速比理论转速略大，随着减速度值的增大，内圈转速降得越快，保持架实际转速与保持架理论值的差值越大，当减速度为45 rad/s2时，保持架开始呈现出负打滑，且随着减速度值的增大，保持架平均打滑率的绝对值也逐渐增大，这表明保持架负打滑效应逐渐增强。

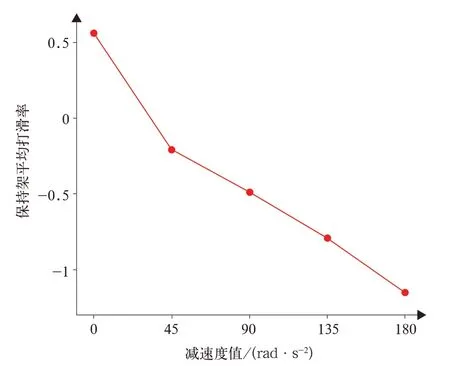
图7 不同减速度下保持架平均打滑率

不同减速度下保持架质心沿x、y方向位移的RMS值统计图如图8所示。通过图8分析可知，保持架质心沿x、y方向位移的RMS值随减速度值的增大而增大，这说明减速度值的增大会导致保持架质心沿x和y两侧方向的位移量增大。通过减速度为90 rad/s2时滚子与保持架的接触力（如图9所示）和滚动体与保持架的受力分析示意图（如图10所示）可以发现，减速工况下，滚子与保持架间的碰撞主要发生在非承载区和承载区的前半段，此时滚子对保持架的作用力有沿x和y负方向的分力。减速度值越大，滚子和保持架速度减小得越快，此时滚子对保持架兜孔的作用力越大，导致保持架质心沿x和y方向的位移量变大。

图8 不同减速度值下保持架质心位移RMS值

图9 减速度为90 rad/s2时滚动体与保持架的接触力

当列车以300 km/h匀速行驶时，轴箱轴承匀速转动，保持架质心的速度偏差比为0.478 56；当轴承内圈以45 rad/s2的减速度减速时，保持架的质心速度偏差比增加至0.485 43，并且保持架质心速度偏差比随着减速度绝对值的增加也逐渐增加，如图11所示，从而导致保持架运动不稳定性增加。因为随着减速度绝对值的增加，滚子与保持架间的碰撞力的变化程度和碰撞次数都相对增加，导致保持架运动失稳。