迭代OFDM/OQAM系统时域时频偏估计方法
2023-01-04邱上飞薛伦生孟新强
邱上飞,薛伦生,孟新强
(1.空军工程大学航空机务士官学校,河南 信阳 464000;2.空军工程大学防空反导学院,陕西 西安 710051)
0 引言
正交频分复用/交错正交幅度调制(orthogonal frequency division multiplexing/offset quadrature amplitude modulation, OFDM/OQAM)系统通过采用具有良好时频聚焦特性的原型滤波器,具有容量大、频谱利用率高、抗干扰性强等优点[1-3]。基于这些优点,其一度被视为5G通信的备选方案之一[4],同时,有很多学者将其应用在电力线通信[5]、对流层散射通信[6]、水下通信[7]以及海上通信[8]等场景中。但是,由于没有了循环保护前缀,使得OFDM/OQAM系统对系统时频同步误差非常敏感,因此,为了保证系统的数据传输精度,良好的时频偏估计与补偿环节就显得非常必要了[9]。
目前,对于OFDM/OQAM系统时频偏估计方法研究主要分为盲时频偏估计方法[10-14]与基于数据辅助的时频偏估计方法[15-20]。盲时频偏估计方法无需插入导频,能够节约系统的频谱资源,但是随着系统对于估计精度要求的提升,其观察时长和捕获时间加长,复杂度较高,不能满足系统对实时性的要求。
基于数据辅助的时频偏估计方法利用插入的导频进行计算,虽然会降低系统频谱利用率,但实用性更强。文献[15]在考虑信道移动及色散的前提下,提出了一种基于最大似然准则的离散导频时频偏估计方法。文献[16—17]中提出了一种频域内的时频偏估计方法,该方法适用于不同的导频结构,具有较大的灵活性。文献[18]则提出了另外一种频域内的时频偏与信道联合估计方法,相比于文献[17]中的方法,该方法的估计范围更大,且精度更高;但是该方法的导频结构导频数量相对较少,容易产生计算误差。文献[19]在最小二乘(linear square,LS)估计的基础上,提出了一种在时域内利用周期导频序列的修正最小二乘(modified linear square,MLS)时频偏估计方法,获得了稳定的时频偏估计性能。文献[20]则是在最小二乘估计的基础上,提出了另外两种时频偏估计方法,均获得了不错的时频偏估计性能。这三种方法性能各有优劣,但均只对系统时频偏进行了一次估计操作,且在进行时偏估计时并未考虑频偏对于系统的影响,这必然会影响系统的时偏估计精度,进而影响频偏估计精度。
针对这三种方法存在的问题,本文采用三种方法中的最优算法进行时偏和频偏估计,同时对时频偏估计环节进行迭代,提出一种基于迭代的OFDM/OQAM系统时频偏估计方法,提升系统的时频同步性能,提高系统数据传输精度。
1 OFDM/OQAM系统时域时频偏估计原理
为便于分析,本文采用OFDM/OQAM系统的离散时间系统模型,其基带发送信号的离散形式描述如下[19]:
(1)
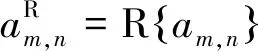
信号经过多径信道传输后,传输信号在接收端受到系统时偏、载波频偏与信道噪声的影响后的离散基带信号r(k)能够表示为
(2)
式(2)中,时偏τ∈;频偏ε为归一化后的载波频偏;h(k,l)为信道在k时刻第l径的时变抽头增益系数;Lh为信道最大抽头数,且Lh=τmax/Ts;τmax与Ts分别为信道最大时延扩展与符号采样周期;ω(k)表示均值为0,方差为的加性高斯白噪声序列。
OFDM/OQAM系统时域时频偏估计方法的原理是在发送端发送数据之前添加一些具有重复结构的导频训练序列,之后在接收端利用与这一部分导频相对应的接收信号进行计算,进而得到系统的时偏与频偏估计值。
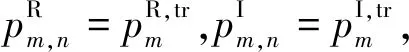
(3)
式(3)中,原型滤波器g(k)的长度为Lg=KM,K为交叠因子,即,当且仅当k∈{0,1,…,KM-1}时,原型滤波器的值不为零。结合式(1),可以得出,当k∈{0,1,…,KM-1}时,该组导频的时域合成信号存在如下关系:
sT(k+M)=sT(k)。
(4)
结合式(3)和式(4),能够构建具有L-K个重复结构的导频训练序列,即,在频域内发送相同的OFDM/OQAM系统导频符号,就能够在时域内构建出具有周期特性的训练序列。
假设信号在高斯信道中传输,则式(2)中的等效基带信号r(k)能够表述为
r(k)=ej2πεks(k-τ)+v(k)。
(5)
根据训练序列的重复特性,可以通过求解下式最小化问题来求解时偏τ和频偏ε:
(6)
进一步推导,可以将式(6)写为
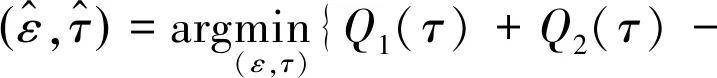
(7)
式(7)中,arg{·}为解相位因子操作,且
(8)
(9)
(10)
对式(7)进行分析可知,当系统的时间偏移τ为某一值时,取式中第三项的余弦项的值为1时,式(7)能够取得最小值,此时可以计算出系统频偏ε的估计值为
(11)
此时,式(7)可以简化为
(12)
可以计算出系统时偏τ为
(13)
为了进一步提升系统的时频偏估计性能,取Q(τ)=Q1(τ)+Q2(τ),取式(13)中目标函数与Q(τ)的比值,可以得到修正的时偏估计表达式:
(14)
以及修正的频偏估计表达式:
(15)
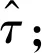
文献[20]中基于相同的特性提出了另外两种估计方法,分别为TR1和TR2方法,TR1方法求解时频偏的表达式分别为
(16)
(17)
TR2方法求解时频偏的表达式分别为
(18)
(19)
(20)
(21)
文献[19]对上述三种方法进行了详细的性能仿真比较,仿真结果表明,在时偏估计性能方面TR2方法优于另外两种方法,在频偏估计性能方面则是MLS方法优于另外两种方法。
2 基于迭代的时频偏估计方法
对上述三种方法进一步分析可以看出:相比于MLS方法与TR1方法对接收信号序列进行二阶自相关操作,TR2采用的是接收信号序列与发送信号序列的四阶互相关,其能够得到较大的相关峰值,进而有着更好的时偏估计性能;同时,MLS方法与TR1方法采用的自相关操作在进行频偏估计时能够消除一部分信道的影响,因而TR2方法在频偏估计性能方面不如另外两种方法;此外,三种方法均只对系统时频偏进行了一次估计操作,且在进行时偏估计时并未考虑频偏对于系统的影响,这必然会影响系统的时偏估计精度,进而影响频偏估计精度。
针对上述方法的不足,本文提出了两点改进:首先,对于系统的时偏估计采用发送信号与接收信号的四阶互相关,对系统频偏估计则采用接收信号的二阶自相关进行;其次,对系统时频偏估计环节进行迭代,在获得时频偏的大致估计值后,使用该估计值对系统进行时频偏补偿,之后再多次对残余的时频偏值进行估计以及补偿。
需要注意的是,系统在第一次时偏估计后,能够对大部分系统时偏值进行补偿,假若在后续的估计环节中继续沿用第一次时偏估计的表达式,必然会增加系统计算复杂度,因此,在后续的时频偏估计中,采用发送信号与接收信号的二阶互相关进行时偏估计。对于系统的迭代次数,可以通过设定一个门限值,对系统已知的导频值与解调出来的导频值取差值,当差值小于门限值时,即结束迭代过程,完成对系统时频偏的估计以及补偿环节。
本文方法首次时偏和频偏估计表达式分别为
(22)
(23)
式中,R(τ),S(τ)和T(τ)的表达式分别如式(10)、式(20)和式(21)所示。
第二次及以后的时频偏估计环节中,频偏估计表达式不变,时偏估计表达式为
(24)
式(24)中,
(25)
(26)
设门限值为ζ,系统导频值为Pm,本文方法的主要步骤如下:
步骤1 按照式(22)与式(23)计算出系统的初步时频偏估计值,并按照估计值对系统进行时频偏补偿;
步骤2 对系统导频序列进行解调等相关操作,获得导频估计值P′m;
步骤3 对ψ=|Pm-P′m|与门限值ζ进行比较,若ζ>ψ,则进入到步骤5,否则进入到步骤4;
步骤4 对补偿后的接收信号按照式(24)与式(23)计算系统时频偏值,并且按照估值对系统进行时频偏补偿,返回步骤2;
步骤5 完成对系统时频偏的估计,对系统接收信号完成接收端其他处理操作。
3 仿真验证
通过仿真对本文方法的性能进行验证。系统的仿真参数如表1所示。仿真中,归一化后的时偏均匀分布在区间[0,M/2],频偏则是均匀随机分布在[-0.25,0.25]。此外,为了突出时频偏估计方法的性能,仿真中的信道估计环节均为理想的信道估计。
由上一章的分析可知,TR2方法具有最好的时偏估计性能,因而其整体性能最好,MLS方法次之,TR1方法最差。因此,本文只选择前两种方法与本文方法进行仿真性能比较。图1和图2分别为三种方法的时偏估计与频偏估计的均方误差(mean square error,MSE)性能比较。图中,Pro-n代表的是本文方法经过n次迭代后的结果。

表1 OFDM/OQAM系统仿真参数Tab.1 OFDM/OQAM system simulation parameters
由于本方法在第一次计算系统时偏时,使用的是与TR2方法相同的计算公式,因而未经过迭代的本文方法具有与TR2方法相同的时偏估计性能,在性能仿真比较中未进行考虑。由图1可以看出,TR2方法在时偏估计性能方面远远优于MLS方法,其相比于MLS方法最多能够获得5 dB的性能提升。相比于TR2方法和MLS方法,本文方法在经过迭代环节后,能够进一步消除残余时偏的存在,进而提升系统的时偏估计性能。具体来说,当本文方法迭代次数为1时,相比于TR2方法与MLS方法,其性能提升最大分别可以达到2.5和7.5 dB;当迭代次数为2时,则为3.3和8.3 dB。但是当迭代次数增加到3时,与迭代次数为2时性能相差不大,这也说明本文方法在经过两次迭代之后就可以被认为取得了最优的时偏估计性能。
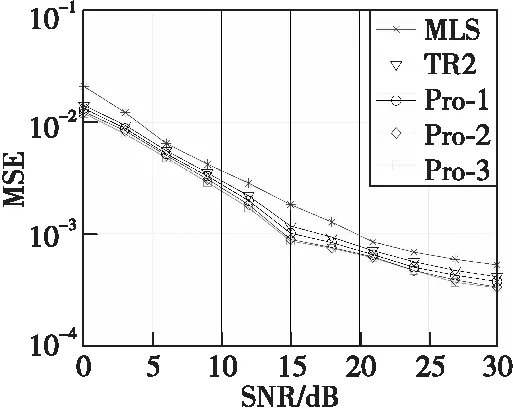
图1 系统时偏估计性能比较Fig.1 TO estimation performance comparison
图2的仿真结果验证了对三种传统方法的性能分析,即MLS方法能够拥有比TR2方法更好的频偏估计性能。同时,未经过迭代的本文方法能获得比上述两种方法更优的频偏估计性能,能够获得约0.8 dB的性能提升。这是因为本文方法在估计系统时偏值时采用的是与TR2方法相同的公式,而在计算时偏估计值时采用的是与MLS方法相同的计算公式,综合了两种方法的优点,因而能够拥有更优的性能。与时偏估计一样,当本文方法的迭代次数达到2时,能够获得比较好的性能,其相比于MLS方法和TR2方法能够分别获得7.5和9.0 dB的性能提升。
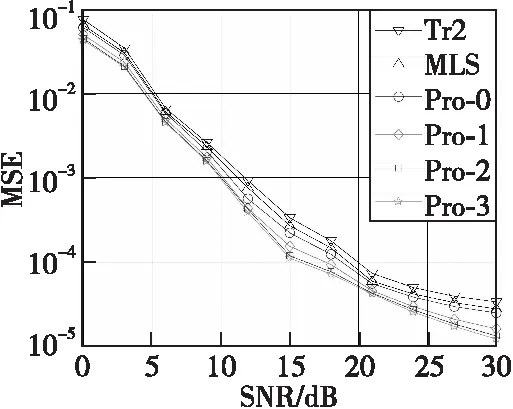
图2 系统频偏估计性能比较Fig.2 CFO estimation performance comparison
最后,对系统的误码率(bit error ratio, BER)性能进行仿真比较,仿真结果如图3所示。由图3可以看出,由于TR2方法在时偏估计方面的良好性能,其相比于MLS方法在BER性能方面有着很大的提升。同时,由于本文方法结合了MLS方法与TR2方法各自的时频偏估计的优点,因而本文方法能够获得比这两种方法更优的性能。此外,随着迭代次数的增加,系统的时频偏得到了进一步的补偿,这也是本文方法能够获得时频偏估计性能提升的重要原因。从图3中也可以看出,当迭代次数达到2之后,随着迭代次数的提升,系统BER性能几乎不变。
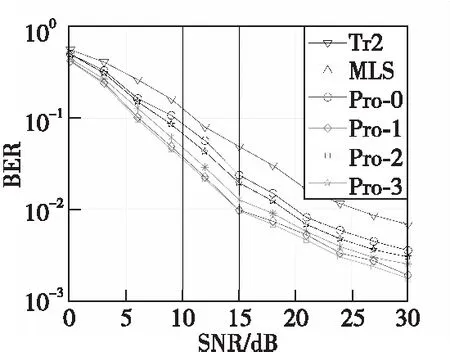
图3 系统BER性能比较Fig.3 BER performance comparison
以上仿真结果验证了本文提出的方法能够实现系统时频偏估计性能较大的提升,但是引入迭代环节必然会增加系统的复杂度,导致系统实时性变差,这也是本文方法下一步所需要改进的方向。
4 结论
本文对三种经典的OFDM/OQAM系统时频偏估计方法进行了分析比较。在此基础上,结合三种方法的优点,同时引入迭代环节,提出一种基于迭代的时频偏估计方法。仿真结果表明,该方法以一定的计算复杂度和系统实时性为代价,取得了更好的时频偏估计性能,进而提升系统数据的传输精度。
