复杂信任网络群组综合评价方法及应用研究

曾守桢，顾佳星，叶 军

(1.宁波大学 商学院， 浙江 宁波 315211；2.宁波大学 土木工程与地理环境学院， 浙江 宁波 315211)

一、 引 言

现实生活中，因评价对象涉及专业面广、领域复杂，仅由单个个体做出的评价主观性较强，评价结果往往过于片面，无法充分挖掘和体现评价对象的内在特征。因此，需要由多评价个体组成的群组对目标对象进行综合评估以体现群组智慧，进而获取更优更合理的评估方案。目前，学界对群组综合评价方法进行了较为广泛的研究，主要针对评价信息的表达方式、信息集成方法、群组评价技术等问题展开研究，具体如下：

关于评价信息表达方式的研究，学者Zadeh(1965)[1]提出了模糊集(Fuzzy Set，FS)的概念，它是由精确数学到模糊数学的重大突破，克服了传统数学理论只有“非此即彼”两种状态的缺陷，是处理复杂评价与决策环境中不确定性和模糊性的重要工具。考虑到FS通过隶属度仅描述事物的支持和反对两种情形，无法体现出中立的情况，Atanassov(1986)[2]提出了直觉模糊集(Intuitionistic Fuzzy Set，IFS)的概念，通过隶属度μ、非隶属度ν和犹豫度π等三要素刻画模糊性特征，同时反映了支持、反对和中立三种情形。但是随着评价与决策环境越发复杂，IFS在约束条件(0≤μ+ν≤1)下往往无法全面测度和表达不确定信息。于是，Yager(2014)[3]以及Senapati和Yager(2019)[4]相继提出了毕达哥拉斯模糊集(Pythagorean Fuzzy Set，PFS)和Fermatean模糊集(Fermatean Fuzzy Set，FFS)的概念，其中，PFS和FFS的隶属度μ与非隶属度ν分别满足约束条件：0≤μ2+ν2≤1和0≤μ3+ν3≤1。相较于IFS和PFS，FFS的表达范围更为广泛、表达模糊信息的能力更强。考虑到实际复杂的评价环境，专家有时无法准确给出相应的隶属度和非隶属度值，往往用一个区间来表示，因此学者Jeevaraj(2021)提出区间Fermatean模糊集(Interval-valued Fermatean Fuzzy Set，IVFFS)的概念[5]，其为评价专家对不确定信息的测度提供了极大的便利。

目前，IFS和PFS等集成方法的研究得到广大学者的关注，研究成果也颇为丰富[6-12]。由于FFS比IFS和PFS在表达范围和能力上更具优势，因此关于FFS集成方法的研究也日趋丰富，如Senapati和Yager(2019)[4]提出了Fermatean模糊加权(幂)平均/几何集成算子；Rani和Mishra(2021)[13]提出了一系列Fermatean模糊Einstein集成算子，包括Fermatean模糊Einstein(有序)加权平均/几何算子；Tan等(2022)[14]进一步提出了基于Frank的Fermatean模糊加权集成算子。由于IVFFS理论是2021年提出的相对比较新的模糊测度方法，因此关于IVFFS集成方法的研究并不多见，目前仅发现Rani和Mishra(2022)[15]提出的区间Fermatean模糊加权平均和几何集成两种集成算子。

关于群组综合评价理论的研究，一个新的研究趋势是与社会网络理论的结合，主要是考虑社会网络中专家个体间的信任关系对专家权重与共识达成的影响。文献[16-23]提出了基于专家间的网络信任大小来获取专家权重的方法，专家的信任度越高，相应的权重越大。关于共识达成与反馈机制的研究，如Wu等(2017)[16]提出一种基于信任的建议生成机制，旨在根据群组综合评价意见对未达成共识的专家意见进行调整；Tian等(2018)[20]提出一种双重反馈机制对未达成共识的专家进行意见和权重的双重修改；Wu等(2015)[17]提出一种反馈推荐机制以提高群组共识度，其中专家意见向群组综合评价意见或其余专家综合评价意见方向调整；Liu等(2017)[24]提出一种信任诱导推荐机制，其中由共识度构造专家间的信任关系，进而根据信任关系调整未达成共识的专家意见。

上述关于区间Fermatean模糊集成和群组评价的研究存在以下两个方面的缺陷：(1)现有区间Fermatean模糊信息集成的研究比较匮乏，已有的加权和几何集成方法缺乏灵活性，无法满足更为复杂评价问题的需要；(2)群组评价专家间的社会网络信任关系对评价共识和评价结果具有重要影响，但目前未见考虑网络信任的区间Fermatean模糊群组评价相关研究；(3)现有关于专家意见反馈机制的研究虽然结合了信任关系特征，但主要侧重将未达成共识专家的评价意见向群组综合评价意见方向调整，并未真正发挥信任关系在意见反馈机制中的作用，没有考虑评价专家对反馈意见的接受意愿。事实上，专家更愿意相信其信任的专家的评价意见。少数文献有基于信任关系的专家意见调整研究，但忽略了未达成共识的专家对其他专家信任程度的差异化问题。

综上，为改进现有研究的缺陷，丰富模糊群组评价理论，本文提出一种基于区间Fermatean模糊信息的信任网络群组综合评价方法。具体而言，首先提出了一种基于Frank方法的区间Fermatean模糊集成技术，弥补了现有方法无法体现灵活性特征的不足；设计了专家个性化意见反馈机制，在此基础上进一步提出信任共识交互模型，弥补了专家意见反馈阶段信任关系的作用无法真正体现的缺陷，同时权衡了专家对反馈意见的接受意愿。此外，分别设计了基于信任水平和熵权法的专家权重和指标权重确认方法。

二、 预备知识

本节简要回顾FFS、IVFFS和Frank算子的相关理论知识，同时定义了IVFFS的得分函数、精确函数以及距离测度。

定义1设I={Y1,Y2,…,Yn}为一论域，则定义在I上的一个FFS可表示为：

F={〈Y,μF(Y),νF(Y)〉|Y∈I}

(1)

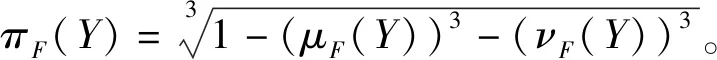
定义2设I={Y1,Y2,…,Yn}为一论域，则定义在I上的一个IVFFS可表示成式(1)的形式，其中μF:Y→Int[0,1]，νF:Y→Int[0,1]，μF(Y)和νF(Y)分别表示元素Y属于集合F的隶属度和非隶属度，且满足条件supY(μF(Y))3+supY(νF(Y))3≤1。由于μF(Y)和νF(Y)为[0,1]上的子区间，故可表示成上下界的形式，即μF(Y)=[μFL(Y),μFU(Y)]，νF(Y)=[νFL(Y),νFU(Y)]。因此，IVFFS又可表示为：

F={〈Y,[μFL(Y),μFU(Y)],[νFL(Y),νFU(Y)]〉|Y∈I}

(2)

为比较区间Fermatean模糊数的大小，本文定义如下的得分函数和精确函数：

定义3设F=〈[μFL,μFU],[νFL,νFU]〉为一个IVFFN，则其得分函数定义为：

(3)

精确函数定义为：

(4)

则对于任意两个区间Fermatean模糊数F1和F2，有

(1)若S(F1)>S(F2)，则F1>F2；

(2)若S(F1)=S(F2)，则

1)若H(F1)>H(F2)，则F1>F2；

2)若H(F1)=H(F2)，则F1=F2。

定义4对区间Fermatean模糊数F1=〈[μFL1,μFU1],[νFL1,νFU1]〉和F2=〈[μFL2,μFU2],[νFL2,νFU2]〉，它们间的距离测度定义为：

(5)

定义5Frank T-模和Frank S-模函数的定义如下：

(6)

(7)

Frank T-模和S-模的两大优点：一是Frank T-模和S-模具有一般T-模和S-模的特性，二是公式中含有参数γ，因此在决策过程中专家可根据实际问题的需要选取适当的参数值。

三、 区间值Fermatean模糊Frank集成算子

(一) 区间值Fermatean模糊Frank运算法则

基于定义5中的Frank函数，下面我们提出区间值Fermatean模糊的Frank运算法则。

定义6设F=〈[μFL,μFU],[νFL,νFU]〉和Fi=〈[μFLi,μFUi],[νFLi,νFUi]〉(i=1,2)为三个区间Fermatean模糊数，则有：

(1)

(2)

定义7设Fi=〈[μFLi,μFUi],[νFLi,νFUi]〉(i=1,2)为任意两个区间Fermatean模糊数，且λ,λ1,λ2>0，则有如下性质：

(1)F1⊕F2=F2⊕F1；

(2)F1⊗F2=F2⊗F1；

(3)λ(F1⊕F2)=λF1⊕λF2；

(4)λ1F1⊕λ2F1=(λ1+λ2)F1；

限于篇幅，以上性质的证明不再详细展开。

(二) 区间值Fermatean模糊Frank加权平均算子

(8)

定理1设Fi=〈[μFLi,μFUi],[νFLi,νFUi]〉(i=1,2,…,n)为一组区间Fermatean模糊数，则IVFFFWA算子的集成结果仍然为区间Fermatean模糊数，且：

(9)

证明：

(1)当n=1时，式(9)成立，即ωF=1·F=F=〈[μFL,μFU],[νFL,νFU]〉。

(2)当n=2时，有

ω1F1⊕ω2F2=

因此，当n=2时，式(9)仍成立。

(3)假设当n=k时，式(9)成立。则当n=k+1时，有

因此，当n=k+1时，式(9)也成立，综上所述，对于任意的n，式(9)成立。

再者，

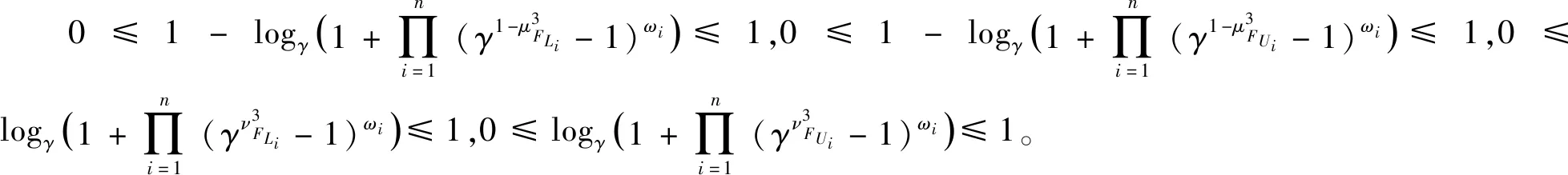
因此，IVFFFWA算子集成后仍然为IVFFN，证毕。

(1)幂等性：若Fi=F=〈[μFL,μFU],[νFL,νFU]〉，则有IVFFFWA(F1,F2,…,Fn)=F

(三) 区间值Fermatean模糊Frank加权几何算子

(10)

定理3设Fi=〈[μFLi,μFUi],[νFLi,νFUi]〉(i=1,2,…,n)为一组区间Fermatean模糊数，则IVFFFWG算子的集成结果仍然为区间Fermatean模糊数，且

(11)

定理3的证明与定理1类似，限于篇幅，此处省略。而且，IVFFFWG同样具有幂等性、交换性、单调性和有界性。

下面对IVFFFWA和IVFFFWG算子的特殊情形进行讨论，

(1)当γ→1时，IVFFFWA算子退化成区间值Fermatean模糊加权平均(Interval-valued Fermatean fuzzy weighted average，IVFFWA)算子[15]，即

(2)当γ→+∞时，则有IVFFFWA算子退化成传统的区间值加权平均(Interval-valued weighted average，IVWA)算子，即

(3)当γ→1时，IVFFFWG算子退化成区间值Fermatean模糊加权几何(Interval-valued Fermatean fuzzy weighted geometric，IVFFWG)算子[15]，即

(4)当γ→+∞时，则有IVFFFWG算子退化成传统的区间值加权平均(Interval-valued weighted average，IVWA)算子，即

四、 评价专家权重与信任共识交互模型

在实际群组评价过程中，评价专家知识背景和经验差异等因素往往导致初始评价意见难以达成一致，由此产生共识达成问题。基于未达成共识的评价信息做出的决策，其结果的科学性和合理性难以保证，因此群体共识达成对决策结果至关重要。随着web2.0技术的普及，专家间的联系更加紧密，相应的专家间的信任网络也日益凸显，评价专家间的信任关系对专家权重和共识达成具有重要的影响，因此有必要研究基于专家信任的专家权重方法和共识达成机理。

(一) 评价专家权重

图1 评价专家间的信任关系网络

在群组综合评价过程中，评价专家间或多或少都存在一定程度的信任关系，将信任关系集与评价专家集合组成的网络结构，称为信任网络。具体而言，一个信任网络可记为G=〈E,TR〉，其中E表示评价专家集，TR表示信任关系的集合，图1为由4位评价专家组成的信任网络：

图1中有向箭头表示评价专家间的信任关系，评价专家集E={E1,E2,E3,E4}。由于评价专家通常采用“非常信任”，“比较信任”，“一般信任”等语言术语表达对他人的信任程度(周晓阳等，2020)[25]，因此本文利用语言术语表达评价专家间的信任关系。设S={s-τ,s-τ+1,…,s0,…,sτ-1,sτ}为语言术语集，其中τ为正整数。则评价专家间的信任网络可表示成如下的信任关系矩阵形式：

其中，信任关系TRst(s,t=1,2,3,4)用语言术语sα(α=-τ,-τ+1,…,0,…,τ-1,τ)来表示。

由于定性语言变量无法适用于定量的评价专家权重的求解过程，因此本文利用周晓阳等(2020)[25]中的转化方法将语言术语定量化，转化为如下信任程度形式，表达式如下：

(12)

其中，αTRst表示用语言术语st表示信任关系TRst时st的下标，进而，可将图1中信任关系矩阵TR转化为信任程度矩阵TD：

基于上述信任程度矩阵TD，可计算评价专家Et(t=1,2,3,4)的权重：

(13)

(二) 基于信任网络的共识交互模型

在区间Fermatean模糊环境下，本节提出一种基于信任网络的共识交互模型，以弥补现有共识交互模型未发挥信任关系在共识达成中的真正作用的缺陷，同时充分考虑了评价专家对意见的接受意愿。具体可分为基于区间Fermatean模糊距离测度的共识度度量、识别与个性化反馈机制三个方面：

层次1:从指标层面出发，专家Et对方案Ζi在指标Cj下的共识度为：

(14)

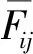
层次2:从方案层面出发,专家Et对方案Ζi的共识度为：

(15)

层次3:从专家层面出发,专家Et的共识度为：

(16)

基于式(14)—(16)可得各评价专家的共识度，进而可根据以下三个层次的共识度识别模型，识别未达成共识专家的评价意见，同样分为指标、方案和专家三个层次：

层次1:找出所有共识度低于共识阈值δ的评价专家，表示如下：

EXPCH={t|CIt<δ}

(17)

层次2:基于层次1，找出所有共识度低于共识阈值δ的方案，表示如下：

(18)

层次3:基于层次2，找出所有共识度低于共识阈值δ的指标信息：

(19)

根据式(17)—(19)识别出未达成共识的专家的评价意见后，需对其进行意见调整以提高群组共识度。下面提出一种个性化反馈机制调整专家评价意见，表达式如下：

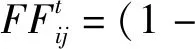
(20)

其中，

(21)

式(21)中l表示专家Et有l个信任的专家，ρr(r=1,2,…,l),l≤K表示专家Et对专家Er的信任程度占专家Et对所有信任专家信任程度之和的比重，假设专家Et对专家Er(r=1,2,…,l),l≤K的信任程度用TDtr(r=1,2,…,l)表示，则有：

(22)

五、 区间Fermatean模糊信任网络群组综合评价方法

在对专家评价信息集成之前，还需获得评价指标的权重，否则无法获得各方案的综合评价值，同时无法进一步对方案排序与择优。因此，本文将提出一种基于区间Fermatean模糊熵的指标权重计算方法，具体过程如下。

(23)

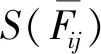
进而，基于式(23)可得评价指标Cj权重wj，表达式如下：

(24)

基于以上指标权重计算过程，结合区间Fermatean模糊Frank算子、评价专家权重以及信任共识交互模型，下面提出区间Fermatean模糊信任网络群组综合评价方法，其评价流程如图2所示。

图2 IVFF信任网络群组综合评价方法

具体评价过程如下：

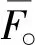
步骤2：利用式(14)—(16)计算评价专家共识度，进而基于式(17)—(19)识别未达成共识的专家的评价意见，然后通过式(20)—(22)对未达成共识的专家评价意见进行反馈调整。

步骤3：若调整后评价专家共识度都大于共识度阈值，则继续步骤4；否则，重复步骤2中式(14)—(19)的计算过程，直至评价专家共识度都大于共识度阈值为止。

步骤4：基于共识达成后的群组综合评价矩阵，结合式(23)—(24)计算评价指标权重，进而基于式(9)或式(11)计算各方案的综合评价值。

步骤5：根据步骤4的综合评价值，结合式(3)—(4)对方案进行择优排序。

六、 案例分析

(一) 本科生统计设计能力评价研究

为进一步提高商科类专业本科生对统计学的学习兴趣，加强统计思维和统计素养的培养，统计设计能力的提高，某高校商学院对统计学的教学目标、内容和方法等方面进行了一系列改革。在课程定位方面，虽然在统计学中需要用到大量的数学理论、方法、技巧，但统计学更多地侧重于数据，侧重于应用。因此在商科专业的统计学教学过程中不侧重于统计方法的数学原理推导，而注重阐明统计方法中隐含的统计思想以及这些方法在实际领域中的具体应用。在教学方法上，注重将理论与实际相结合，倡导学生自主学习、自主踊跃讨论，着重提高学生应用统计方法解决实际问题的能力。在教学内容方面，从商科类专业学生实际出发，为他们量身定制教学内容，侧重于统计思想、方法的讲解、统计软件工具的使用，并结合实际经济社会管理中的案例进行统计分析，使学生真正意识到统计是一个非常有用的工具。

为了检验统计学课程建设和改革等方面的效果，下面根据统计类学科相关特征，结合相关文献[26-28]，提出高校商科类专业本科生统计设计能力的综合评价指标体系，具体指标含义解释如下。

1.数据收集能力C1。经过统计学课程的学习，学生应当掌握各类数据收集方法和渠道，具备收集、存储和转换各种形式信息的能力。同时，面对数量繁多、类型多样的调查类数据信息，学生还应具备统计调查问卷设计能力，以保证调查问卷数据收集方法的有效性和科学性。

2.数据分析能力C2。指利用统计分析方法并结合数据分析工具(如SAS、SPSS等)，对所收集的数据信息进行统计描述和分析整理，进而以图表化等丰富多样的形式展示数据的特征。

3.统计处理能力C3。指依据合适的统计方法构建统计模型，探索数据背后的规律、逻辑关系和其他特征，进而对经济、社会发展现象进行接受并进行趋势预测分析。

4.应用能力C4。指学生将数据的收集、分析和处理的结果进行归纳总结和应用，进而对社会现象和问题进行更深层次的分析，并以此提出有价值的建议。其中可以展示学生对社会现象的敏锐洞察力和统计拓展能力。

5.数据伦理道德C5。指学生在数据的收集、处理等过程中的道德和伦理问题，学生应树立正确的法治理念，遵守相关道德规范，不收集使用未经授权的数据信息，不得随意公开、泄露隐私数据，同时要做到数据收集的真实性，不得弄虚作假、随意篡改等。

现邀请4位统计学专业领域的相关专家，根据上述5个评价指标对某高校商学院的金融A1、经济A2、会计A3和国际贸易A4等4个专业的本科生统计设计能力进行综合评估。其中4位专家给出的评价信息为表1-4：

表1 专家E1的评价矩阵

表2 专家E2的评价矩阵

表3 专家E3的评价矩阵

表4 专家E4的评价矩阵

步骤1：设评价专家间的信任社会矩阵表示如下(设τ=3)：

首先，将TR矩阵转化为信任程度矩阵TD矩阵，表示如下：

则基于式(12)—式(13)可得评价专家权重，

ω=(0.265,0.294,0.206,0.235)T

其次，利用式(9)并结合表1-4，对专家个体信息进行集成。不失一般性，假设γ=2，可得群组综合评价矩阵Eg，如表5所示：

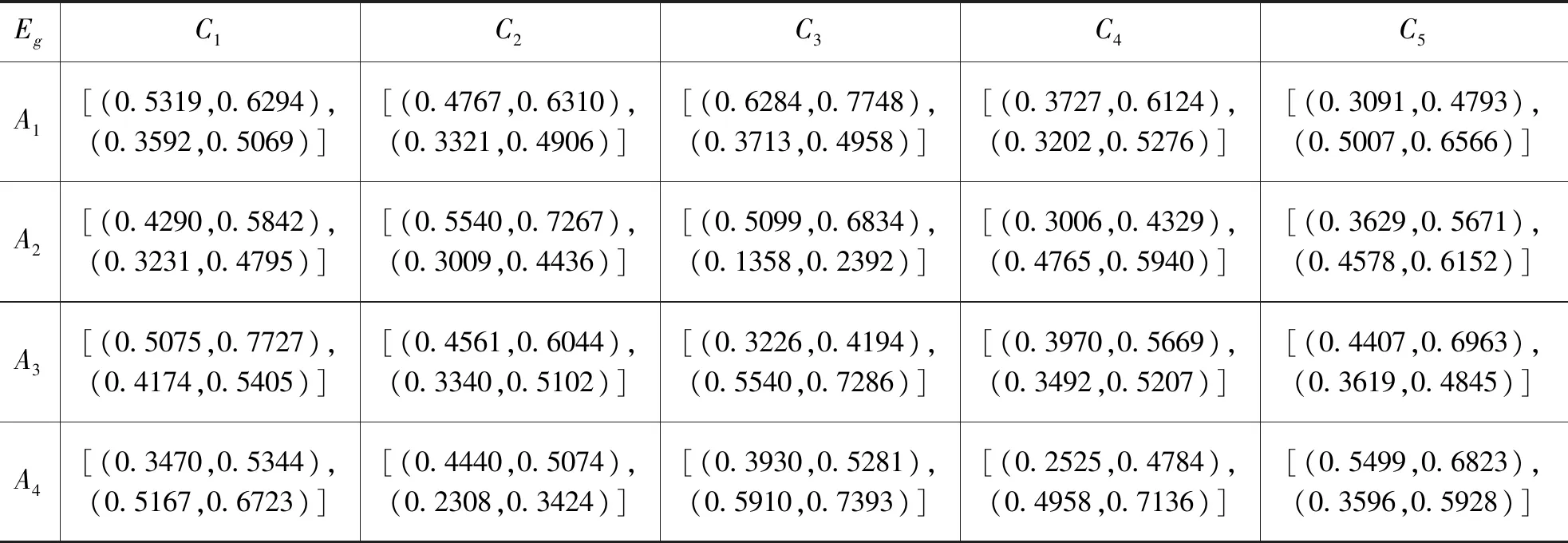
表5 群组综合评价矩阵Eg

步骤2：式(14)—式(16)计算评价专家共识度，即

CI1=0.850,CI2=0.893,CI3=0.783,CI4=0.867。

同时可得方案和指标层面的共识度，即方案层面上的共识度：

CA1=(0.809,0.880,0.833,0.877)，CA2=(0.917,0.839,0.893,0.925)，

CA3=(0.706,0.820,0.873,0.735)，CA4=(0.839,0.842,0.910,0.877)。

指标层面上的共识度：

假设δ=0.8，则根据式(17)—式(19)，可得评价专家E3的共识度CI3<δ，进而可得如下需要调整的专家意见：

基于式(20)—式(22)，可将评价意见修改为：

步骤3：意见修改后可得评价专家新的共识度，即

CI1=0.862,CI2=0.894,CI3=0.848,CI4=0.876。

此时，所有专家共识度均大于阈值δ=0.8，因此无须进一步调整。

步骤4：基于步骤3可得共识达成后的群组综合评价矩阵E′g。

表6 共识达成后的群组综合评价矩阵

根据表6的群组综合评价矩阵，结合式(23)—式(24)计算评价指标权重W，可得

W=(0.2153,0.2380,0.2312,0.1448,0.1707)T。

进而结合式(9)计算各方案的综合评价值，可得：

FA1=[(0.5234,0.6626),(0.3650,0.5201)],FA2=[(0.4662,0.6353),(0.2926,0.4332)],
FA3=[(0.4355,0.6409),(0.4025,0.5590)],FA4=[(0.4092,0.5490),(0.4230,0.5920)]。

步骤5：计算各方案的得分值，可得

SA1=0.5612,SA2=0.5628,SA3=0.5265,SA4=0.4877，

则方案排序为：

A2>A1>A3>A4

因此，方案A2为最优方案。即，商学院经济类专业的本科生统计设计能力最强。

(二) 灵敏度分析

上节实例中我们假定参数γ=2对方案进行排序与择优，下面进一步讨论参数γ的变化对方案排序结果的影响。以基于IVFFFWA和IVFFFWG算子的信任网络群组综合评价方法为例，分别取γ=2,5,10,20,50,100，得到的方案排序结果列于表7。

表7 参数γ变化对方案排序的影响

从表7可以看出，随着参数γ的增大，基于IVFFFWA算子的信任网络群组综合评价方法下的方案排序保持不变，始终为A2>A1>A3>A4，最优方案都为A2，说明基于IVFFFWA算子的信任网络群组综合评价方法具有一定的稳定性，参数γ的变化对方案的排序并不敏感。而基于IVFFFWG算子的信任网络群组综合评价方法下的方案排序存在一定的变化，从A2>A3>A1>A4到A2>A1>A3>A4，说明基于IVFFFWG算子的信任网络群组综合评价方法下的方案排序随参数γ的变化而变化，但不管方案排序如何变化，最优方案都为A2。

(三) 对比分析

为验证本文方法(以基于IVFFFWA算子的信任网络群组综合评价方法为例)的可行性和优越性，现与其他评价方法进行对比分析。首先利用Rani和Mishra(2022)[15]提出的IVFFWA算子集成专家评价信息，然后根据Wu等(2017)[16]提出的共识交互模型调整未达成共识的专家评价意见。假定评价专家权重与本文相同，则根据以上方法的具体计算过程如下。

首先，利用IVFFWA算子集成各专家的评价矩阵，可得群组综合评价矩阵Eg，见表8。

表8 群组综合评价矩阵Eg

其次，利用共识交互模型调整未达成共识的专家评价意见。具体如下，先计算各专家共识度，可得

CI1=0.848,CI2=0.891,CI3=0.784,CI4=0.865

其中，专家E3的共识度CI3<δ=0.8，专家E3在方案和指标层面的共识度分别为：

意见修改后评价专家新的共识度为：

CI1=0.857,CI2=0.894,CI3=0.836,CI4=0.873

所有评价专家共识度均大于阈值，因此无须进一步调整，进而基于共识达成后的群组综合评价矩阵，结合评价指标权重，可得各方案的综合评价值，

FA1=[(0.5185,0.6639),(0.3655,0.5166)],FA2=[(0.4673,0.6387),(0.2925,0.4301)],
FA3=[(0.4368,0.6474),(0.3996,0.5532)],FA4=[(0.4142,0.5527),(0.4183,0.5832)]。

进而计算各方案的得分值，可得

SA1=0.5613,SA2=0.5645,SA3=0.5304,SA4=0.4921。

因此，方案排序结果为A2>A1>A3>A4，与本文方法排序结果一致，最优方案均为A2，说明本文方法是可行的。

通过以上对比分析可以发现，与现有方法相比，本文提出的评价方存在以下两点优势：(1)基于提出的IVFFFWA算子集成专家评价信息，更具灵活性和鲁棒性，专家可根据实际决策环境选择合适的参数γ。此外IVFFFWA算子是IVFFWA算子的一般形式，因此适应性更为广泛；(2)本文所提出的共识交互模型考虑了专家间的信任关系对评价意见调整的影响作用，同时考虑了未达成共识的专家对不同信任专家的信任程度的影响。而共识交互模型以群组综合评价意见为意见调整方向，未考虑信任关系的影响作用。

七、 结 论

本文研究了IVFF信任网络群组综合评价方法及应用，其创新点主要体现在以下几个方面：(1)考虑到专家对他人信任关系表达的偏好习惯，构造基于语言变量的信任表达方式和信任网络，进而转化为信任程度矩阵以计算专家权重；(2)利用IVFFS表达模糊信息的广泛性，结合Frank算子的灵活性和鲁棒性，提出IVFFFWA和IVFFFWG两种新的集成方法；(3)考虑到信任关系对共识达成的影响作用，提出信任共识交互模型调整专家评价意见，提高群组共识度；(4)构建了高校商科类本科生统计设计能力的评价指标体系，提出了IVFF熵权法获取指标权重，使得评价结果更为客观。下一阶段，笔者将在意见反馈阶段考虑未达成共识的专家对信任专家的反馈意见可能存在拒绝的情况(张恒杰等，2021)[29]，即针对专家的调整意愿设计意见调节机制，通过意见反馈和调节机制构建信任共识交互模型。