基于ESGA的纯电动需求响应公交路径规划

郭献超,夏戈松,徐士伟,陈兴博

(1.广州市交通规划研究院,广东 广州 510000; 2.华南理工大学土木与交通学院,广东 广州 510000; 3.广东省交通运输规划研究中心,广东 广州 510000)

近年来随着中国经济的快速发展和城镇化的加快,机动车辆迎来了爆发式增长,大量农村人口进入城市,城市的交通压力越来越大,虽然城市公共交通进入快速发展时期,但仍无法满足市民便捷出行的需求。如今,我国的公共交通已经进入了高速发展轨道,出现了各种各样的交通方式,乘客的出行需求也各不相同,越来越倾向个性化发展的趋势。需求响应公交的出现满足了许多乘客的要求,迎来了快速发展的契机。通过对纯电动需求响应公交路径规划的研究,可以进一步完善我国公共交通体系,增加公共交通的多样性,扩大公共交通的覆盖面和提高乘客对公共交通的满意度。

我国对需求响应公交的研究开始的较晚,国内缺乏需求响应公交的研究内容,尤其是纯电动骑车在需求响应公交的应用研究。Lajunen[1]模拟了不同公交线路,通过对混合动力公交和纯电动公交车能量消耗分析,计算出了它们在运营中的成本效益;李军等[2]根据纯电动公交车的特点,考虑了充电时间、电池状态、充电速率等因素,设计了以营运车辆数最小为目标的纯电动公交车辆调度算法;杨扬等[3]应用整数规划、网络流等基本理论,将纯电动公交调度计划问题转换为网络模型,通过使用列生成方法对模型进行求解;Schilde等[4]研究了不同速度下对DRT服务水平的影响;潘述亮等[5]对包含特殊需求的DRT模型进行了研究;卢小林等[6]提出一种以最小化公交车运营时间为目标的DRT路径优化模型;Masmoudi等[7]研究了异质车辆的DAR的路径规划问题,提出了一种针对已知DAR问题特性的混合遗传算法;Masmoudi等[8]建立了以总路径成本最小化为目标的混合整数非线性规划模型;郑汉等[9]构建需求响应公交服务定制等价分解模型,采用分布式列生成算法对模型进行求解;柳伍生等[10]提出了多需求响应机制下的城市绿色定制公交线网优化模型,利用上车线网和下车线网相结合的分层线网算法对模型进行求解。目前国内外研究主要集中在传统公交的研究中,随着电动车的推广,许多城市都将常规公交换成了电动公交,然而有关电动公交应用在DRT的研究却很少。

纯电动需求响应公交路径规划可分为临时停靠站规划和路径规划两阶段,首先规划纯电动公交临时停靠站点,通常通过K-means算法实现[11]。对公交路径规划可看作是一种特殊形式的带有容量约束的车辆路径问题(CVRP,capacitated vehicle routing problem),不同的是公交车需要从同一场站出发到达同一目的地,目的地与出发地往往不同。车辆路径规划已被证实为NP(non-deterministic polynomial)完全问题,通常设计启发式算法[12-14]求解。遗传算法(GA,genetic algorithm)是通过模拟生物在自然环境中的遗传和进化过程而设计,是一种广泛使用的启发式搜索算法,其选择策略通常是基于轮盘赌(RWSGA,roulette wheel selection genetic algorithm)的概率选择。为了提高算法收敛速度和搜索结果,提出以精英选择遗传算法[15](ESGA,elitist selection genetic algorithm)求解纯电动需求响应公交路径规划问题,并通过实例验证猜想。

1 问题描述和模型建立

1.1 问题描述

纯电动公交车需求响应式公交路径优化问题可描述如下:在研究的区域内,通过调度公交场站若干辆相同的纯电动公交车以满足该区域乘客的出行需求,所有乘客会在预先规划好的区域上车,并到达同一终点站。通过合理规划公交车的行驶路径,以实现企业利润的最大化。该问题属于带有软时间窗的车辆路径问题(VRPSTW),主要分两个部分进行处理。

第一部分为需求响应站点规划,根据乘客的响应点的位置分布,规划若干需求响应站点,用于使需求响应公交车停车接收上车的乘客,并根据站点乘客的期望上车时间分布,确定需求响应站点的时间窗。

第二部分为纯电动公交车路径规划,根据已规划的需求响应站点,规划需求响应公交车的行驶路径,这一部分可以看作带有软时间窗的车辆路径问题,但是由于纯电动公交车的特殊性,在路径规划的过程中,需要根据纯电动公交车的续航状态,合理安排公交车到充电桩的充电策略。为了方便模型建立和求解,有以下基本假设:

(1) 假设纯电动公交车不会载送乘客驶入充电桩充电;

(2) 假设配送车辆为相同车型的纯电动公交车,最大载客量相同、单次充电行驶里程相同;

(3) 假设配送车辆为相同车型的纯电动公交车,最大载客量相同、单次充电行驶里程相同;

(4) 假设从场站发出的纯电动公交车只有两种:第1种是纯电动公交车发出前已经充满电(即k≤P0);第2种是纯电动公交车需要到场站附近的充电桩(即h=n+1)完成快速充电后再发车(即k>P0);

(5) 假设在所研究的网络上分布若干充电桩能够满足纯电动公交车的充电需求;

(6) 假设每辆公交车都只从固定的站场出发,完成所有乘客的接收后,到达统一的目的地;

(7) 假设公交车只在临时停靠站停车,每一区域的乘客需要到最近的临时停靠站乘车;

(8) 假设每辆公交车只开一条线路,每个停靠点只能被公交车访问一次。

基于以上对纯电动需求响应式公交路径规划问题的描述和对模型构建的假设,为方便建立纯电动需求响应公交路径规划的数学模型,定义以下数学符号的含义:

p0表示公交场站充电桩的总数量;

V表示纯电动公交车的集合,v={k},k=1,2,…,p,当k≤p0时,表示纯电动公交车在公交场站已充满电,即满电量发车;当k>p0时,表示纯电动公交车需要去公交场站临近的充电桩充满电后再发车;

S表示纯电动公交车停靠站的合集,v={i},i=1,2,…,n;

E表示路网中充电桩的合集,E={j},j=1,2,…,m,j=1表示公交场站附近的充电桩,即k>p0的车辆需要先到该充电桩充电,再去接送乘客;

A表示路网中所有研究点的合集,即充电桩总数量、纯电动公交车停靠站总数量、出发地、目的地的四者数量之和,A={h},h=0,1,2,…,n,n+1,…,n+m,n+m+1,h=0表示纯电动公交车出发地,h=n+m+1表示纯电动公交车目的地;

O表示乘客的集合,O={a},a=1,2,…,b;

Rk表示所有车辆的单次充电的行驶路径集;

Lk表示所有车辆完成响应需求的行驶路径集;

Cf表示纯电动公交车的启动成本,其与车辆行驶里程无关,而与车辆开行数量有关;

C0表示纯电动公交车的运行成本,其与车辆单位行驶里程成正比;

ETi表示停靠站点i的时间窗上界;

LTi表示停靠站点i的时间窗下界;

C0表示纯电动公交车在充电桩充电的时间;

s表示纯电动公交车在行驶过程中的平均行驶速度;

Ct表示单位时间的惩罚成本;

ua表示乘客a使用需求响应公交车的意愿，ua=1表示乘客具有使用意愿,否则ua=0,a=1,2,…,b;

ea表示乘客a支付需求响应公交的意愿(元);

e0表示企业响应乘客最低支付意愿(元);

ra表示企业对乘客a出行需求的响应意愿,ra=1表示企业响应乘客需求,否则ra=0;

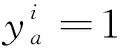
dij表示点i到点j的行驶距离(i,j=0,1,2,…,n,n+1,…,n+m,n+m+1);

d0表示纯电动公交车充满电后的最大行驶里程;

xijk=1表示车辆k从点i行驶到站点j,否则xijk=0(i,j=0,1,2,…,n,n+1,…,n+m,n+m+1,k=1,2,…,p);

Qi表示第i个停靠站点的上车人数,i=1,2,…,n;

Q0表示需求响应公交车的最大载客量。

1.2 模型建立

纯电动需求响应公交路径规划模型的目标函数包括总利润和时间惩罚成本两部分,纯电动需求响应公交的成本包括运营车辆的人力成本和可变成本,收入为乘客支付的乘车票价总和,二者之差为企业的总利润。将公交车超出时间窗的时间量化为时间函数,并通过惩罚函数计入到总优化目标中。综上所述,纯电动需求响应公交路径规划模型如下:

(1)

(2)

当xijk=1时,

(3)

p≤pmax,

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

xijk=0或1,

(13)

k>p0⟹x0,n+1,k=1,

(14)

式(2)表示纯电动公交车到达临时停靠站i超出时间窗的偏离值;式(3)表示纯电动公交车到达临时停靠站i的行程时间;式(4)表示企业可投入用于响应乘客需求的纯电动公交车数量不大于场站公交车的总数量;式(5)表示纯电动公交车只能在接送乘客之前驶入充电桩充电;式(6)表示每辆纯电动公交车的乘客数量不大于公交车的载客上限;式(7)表示每辆纯电动公交车在每次充电后的行驶里程不超过其最大行驶里程;式(8)表示运营企业只响应支付意愿大于等于e0的乘客出行需求;式(10)表示每个临时停靠站点只有唯一的一辆纯电动公交车驶入;式(11)表示每个临时停靠站点只有唯一的一辆纯电动公交车驶出;式(12)表示每辆纯电动公交车的起点都是停车场站,终点都是乘客所要到达的目的地;式(13)表示决策变量被限制为0、1变量;式(14)表示对于未在公交场站充电的公交车,需要先去场站附近的充电桩快速充电,再去接送乘客。

2 模型求解

2.1 基于K-means算法的停靠站规划

首先基于K-means聚类算法规划了公交临时停靠站。K-means聚类算法可以根据样本之间的内在联系,将相同的样本划分为一类,从而将样本整体划分为有不同特征的若干类。K-means聚类的基本流程是先随机选取k个样本作为初始的类中心点。然后计算每个样本与各个种类中心点的距离,把每个样本划分为与其距离最近的类中心点。当所有样本对象都划分完成后,每一类的类中心点会根据类中现有的样本重新计算,这个过程一直重复直到没有中心再发生变化为止。K-means算法的基本流程如图1所示。

图1 K-means算法流程Fig.1 K-means algorithm flow

通过选择欧式距离作为样本点到类中心点的判别距离,其计算公式为

(15)

选择点合集的重心作为每一类的中心点,其计算公式为

(16)

2.2 基于ESGA的路径规划

采用精英种群选择的遗传算法(ESGA,elitist selection genetic algorithm)来求解纯电动需求响应公交路径规划模型,相比于常规的遗传算法,ESGA用每一代种群中适应度较高的个体建立精英种群,精英种群不经过选择的操作直接进入子代种群。因此ESGA相对于常规的遗传算法收敛速度更快,能够更快地获得求解结果。ESGA流程如下:

(1) 编码 编码是为了将需要解决的实际问题转化为可被遗传算法直接求解的数学形式。在现代生物学中,个体的基因代表着不同个体特征。相似的,在遗传算法中经过基因编码的个体代表优化目标的一组可行解。常用的编码方案主要有0、1编码和整数编码两种,本文采用整数编码方案,并根据纯电动公交车行驶路径的实际问题设计了编码方案。

为了解释ESGA中编码过程,通过实例来具体描述。首先,假设路网中有10个规划的公交车临时停靠站和4个充电桩,此外还有公交车起点和目的地2个点。编码的具体流程如下:

步骤1:对路网中的点进行编号,0表示公交车起点,1～10表示临时停靠站,11～14表示充电桩;

步骤2:随机生成1～10不重复的数列,表示公交车到达临时停靠站的顺序;

步骤3:在上述数列随机插入若干个公交车的出发点0,表示需要安排调度的公交车数量;

步骤4:在上述的列序号0后面随机插入若干充电桩编码,表示纯电动公交车需要驶入充电桩充电;

步骤5:将上述的数列作为个体的基因编码;

步骤6:重复步骤2～步骤5,形成一定规模的种群。

上述过程中个体基因编码的示意图如图2所示。

图2 染色体编码Fig.2 Chromosome coding

(2) 适应度计算 ESGA通过选择算子淘汰劣势个体,保留优势个体,适应度为个体选择的依据,目标函数以最小化企业利润的相反数为优化目标,因此,使得目标函数值较小的个体具有较高的适应度。以目标函数的倒数作为计算个体的适应度函数,即

(3) 基于精英保留的选择算子 通过采用了精英个体保留的选择策略,在每一代种群中选择一部分适应度最高的个体,不进行任何操作而直接保留到下一代,剩下部分的个体再通过选择得到。保留的精英个体只占种群的小部分,这是为了避免种群陷入局部最优解。精英个体保留的选择策略可以保证种群的适应度不会增加,加快收敛速度,从而提高最优解的搜索速度。

(4) 交叉算子 遗传算法使用交叉算子通过模拟种群进化中染色体的交叉重组,从而产生子代个体。ESGA采用的交叉算子操作流程如图3所示。

图3 交叉操作Fig.3 Cross operation

(5) 变异算子 遗传算法的变异算子通过模拟种群进化中个体的基因发生突变,进而产生新的个体。ESGA采用两点变异,操作流程如图4所示。

图4 变异算子Fig.4 Mutation operator

(6) 反转算子 反转算子从本质上来说也是基因突变的一种类型,通过逆转染色体基因片段的基因位顺序,从而实现改变染色体的基因。反转算子也可以提高遗传算法搜索能力。ESGA采用的反转算子操作流程如图5所示。

图5 反转算子Fig.5 Inversion operator

(7) 进化终止条件 从理论上来说,当搜索到最优解时,即算法达到100%收敛时,算法会自动终止,然而在实际情况下,由于算法会陷入局部最优很难到达100%收敛。因此,需要设计终止条件以避免算法进入无限迭代循环。遗传算法的终止条件判别主要有以下两种方法:

① 判定相邻两代种群适应度的差值小于某一阈值时终止进化。即当种群进化速度缓慢,种群进化进一步搜索到的最优解对目标函数没有显著变化,继续求解所花费的时间和资源对优化的目标没有显著意义,目前的求解结果已经可以满足实际规划方案了。

② 当种群进化到某一代数时终止循环。第二种方法相对第一种更便于理解和操作,可以根据结果灵活调整。因此选择种群进化最大代数作为种群进化终止的判定条件。

3 实例分析

3.1 实验算例

通过对某区域的公交客流点进行支付意愿调查,该区域内有5个充电站,该区域的公交客流需求点、起终点、充电桩如图6所示。

图6 乘客坐标Fig.6 Passenger coordinates

3.2 求解结果

首先根据坐标信息使用K-means算法将乘客分为32类确定公交停靠站点,如图7所示。然后根据乘客支付意愿确定每个站点的上车人数,公交停靠点信息如表1所列。

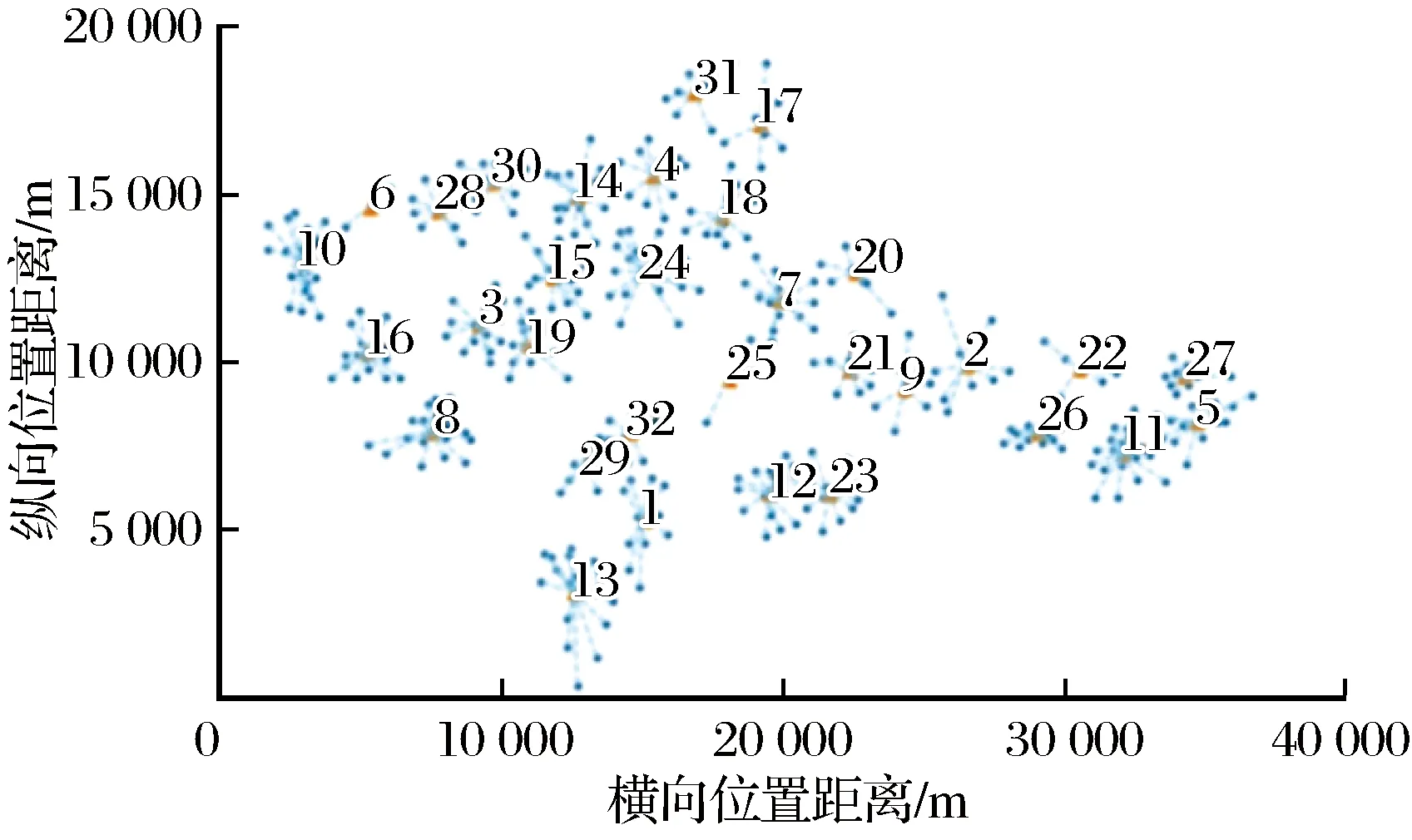
图7 公交停靠点规划Fig.7 Bus stop planning

表1 公交停靠点信息Table 1 Bus stop information table

然后基于ESGA规划纯电动需求响应公交路径,其中种群规模为500,进化代数为1 000,精英种群比例为15%,变异概率为0.1,反转概率为0.1,站场车辆数为14,每辆车的限载人数为30,单位时间惩罚成本为0.5元/min,车辆启动成本司机工资为150元/辆,可变成本为0.49元/km。经过20次的独立重复试验,选取最好试验结果作为最终结果,其进化曲线、不同情况下的车辆路径和计算结果见图8～图11和表2。

图8 进化曲线Fig.8 Evolution curve

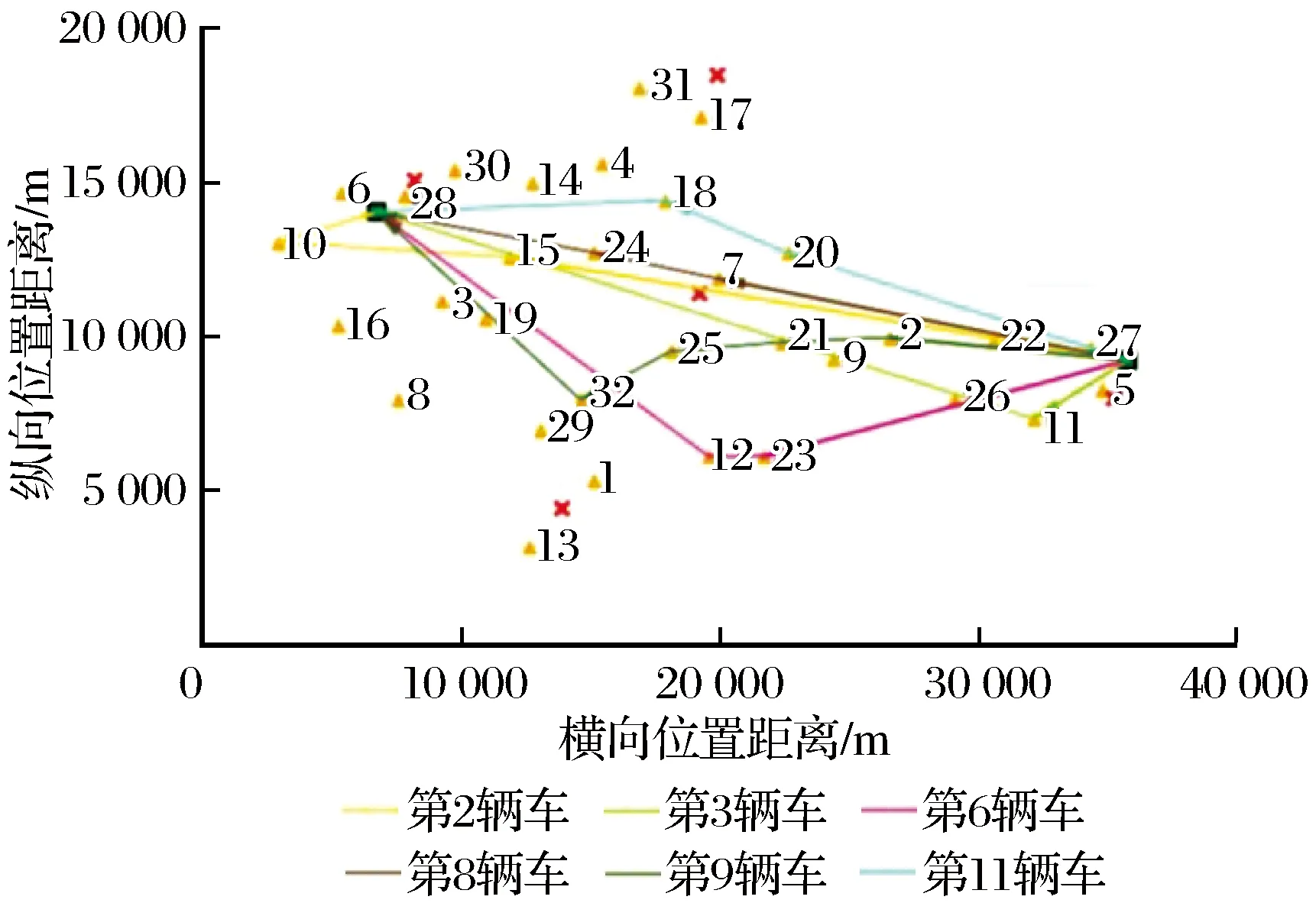
图9 不需充电的车辆行驶路径Fig.9 The driving path of the vehicle without charging

图10 需要充电的车辆行驶路径Fig.10 The driving path of the vehicle that needs to be charged

图11 补充电能车辆行驶路径Fig.11 Supplementary electric vehicle driving path

表2 计算结果Table 2 Calculation result table

由表2可以看出每辆公交车的实际行驶里程均在30 km左右,约为单次充电行驶里程(60 km)的一半。需求响应公交载客率均在50%以上,平均载客率为86.67%,其中11辆车的载客率在80%以上,企业的成本包括人力成本、可变成本和时间惩罚成本3部分,分别为2 100.00元、226.35元和361.97元,企业的总收入全部来源于乘客乘坐响应公交所支付的票价,共7 643元。企业的总利润是企业的总收入减去总成本,为4 954.68元。

4 结语

通过描述纯电动需求响应式公交路径优化问题,构建了特定假设下的数学模型,采用ESGA算法进行问题求解,并通过实际算例验证了ESGA算法,结果表明ESGA算法精英种群的规模设为15%左右时求解结果较好。由于研究水平有限,在对纯电动需求响应公交进行路径规划时有部分问题没有考虑到,存在一定的局限性和不足。今后主要从以下几个方面进行研究和完善:

(1) 此次研究只考虑了单一的纯电动车型,而企业在实际运营过程中,可以根据乘客的个性化需求和实际乘客数量来考虑同时使用多种车型,这样可以节约运营成本，提高需求响应公交满意度。

(2) 此次研究未考虑动态响应需求,在实际运营中会出现新的需求,考虑实时的动态需求不仅可以增加企业的收入,也可以为更多乘客提供需求响应服务。