基于IGOWLA 算子的组合预测方法及应用研究

俞晓军，葛 文，吴春节

（1. 宁波市奉化区城市投资发展集团有限公司，浙江 奉化 315502；2. 宁波市测绘和遥感技术研究院，浙江 宁波 315402）

有序加权平均（OWA）算子是一种集结信息算子，它能有效地集结数据信息，将其推广到λ次幂，得到广义有序加权平均（GOWA）算子。结合诱导变量可获得诱导广义有序加权平均（IGOWA）算子。将IGOWA 算子和广义有序加权对数平均（GOWLA）算子相结合可定义一种新的算子，即诱导广义有序加权对数平均（IGOWLA）算子。国内外学者研究的组合模型[1]大都以误差平方和最小作为建模准则。近些年来，相关性指标被越来越多地应用到组合模型中。本文在此基础上，将向量夹角余弦[2]与诱导广义有序加权对数平均IGOWLA（算子）[3]相结合，构建了一种新的最优组合预测模型。最后通过软土路基沉降预测实例验证此模型方法合理有效，可提高预测精度。

1 基于向量夹角余弦的IGOWLA算子的组合模型的构建

1.1 IGOWLA算子

定义1令：

式中，i=1,2,…m,t=1,2,…N，则称ait为第i种预测模型在t时刻的预测精度[4]。由式（1）可知，预测精度的范围为：ait∊[0 ,1] 。

根据预测连续性原则，获得样本区间上组合模型的最优权系数后，可进行区间[N+1,N+2,…]上的预测，即未来k步的预测值，可采用第i种预测方法近k期拟合平均精度来代表预测区间N+k期预测精度的大小[5]。

定义2 设(u1,a1,u2,a2,…,un,an)为n个二维数组，W=(w1,w2,…,wn)T是与IOWGA算子相关的加权向量，且满足wi=1,wi≥0,i=1,2,…,n。若：

则称函数IGΟWLAw是由u1,u2,…un所产生的n维广义有序加权对数平均算子，简称为IGOWLA 算子，其 中ui为ai的 诱 导 值，λ∊(-∞,0)∪(0,∞) 。u-index(i)是u1,u2,…un第i大的数的下标。从以上公式可知，权系数wi的大小由数组ai,i=1,2,…,n所对应的诱导值的排序位置决定，与数本身的大小和位置无关[6]。

1.2 基本IGOWLA算子组合预测模型

沉降预测中通常以预测精度ait作为预测值xit的诱导值，进而，可将两者组成二维数组a1t,x1t,a2t,x2t,…,amt,xmt。将预测精度序列a1t,a2t,…amt按从大到小顺序排序，设a-index(it)是第i大的预测精度的下标。据定义2可得：

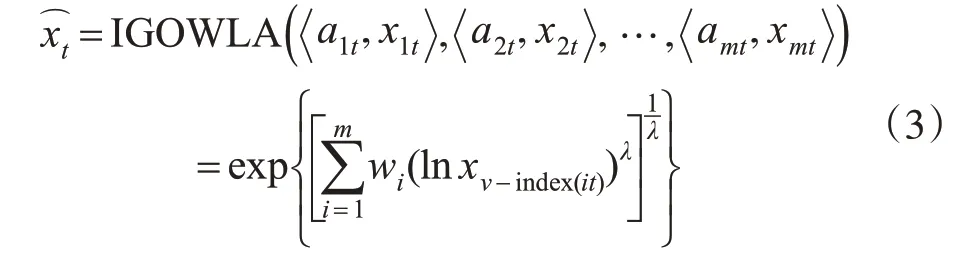
则称上式为第t时刻的IGOWLA算子的组合预测值[7]，由其数学模型可知，基于IGOWLA算子的组合模型的预测精度与单项模型各时刻的拟合精度的大小密切相关，而与各模型各时刻的拟合精度大小密切相关。

定义3 称eit=(lnxt)λ-()λ为第i种单项预测方法在第t时刻的对数λ次幂的预测误差；称et=(lnxt)λ-(̂)λ为广义诱导有序加权对数平均的组合预测值在第t时刻的对数的λ次幂的预测误差。

根据上述定义，可得N期总的组合预测的对数的λ次幂的预测误差平方和s为：

基于IGOWLA算子的最优组合预测模型可表示成如下最优化模型。

令：

式中，i,j=1,2…,m，则称E=(Eij)m×m为m阶广义诱导有序加权对数平均组合预测无量纲化序列的对数的λ次幂的误差信息矩阵。

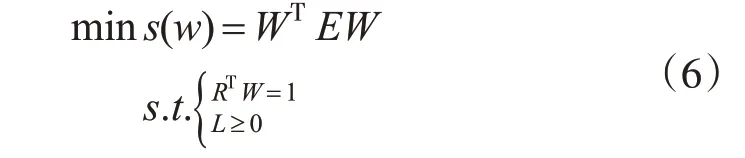
1.3 基于向量夹角余弦的IOWGA算子的组合模型

传统组合模型的建模方式单一，通常采用残差平方和最小准则。为提高建模效率，丰富建模方法，实际建模时，以预测精度作为诱导变量且以向量夹角余弦作为建模准则，构建一种基于向量夹角余弦的IGOWLA算子的组合模型。

由向量夹角余弦的定义可知，ηi为第i种预测模型预测值向量Xi与其对应的实际值向量X的夹角余弦；η为组合预测值向量̂与实际值向量X的夹角余弦，其中，i=1,2,…,m。

组合预测值与实际值对数向量的夹角余弦η可用加权系数l1,l2,…,lm的函数表示，简记为：η（l1,l2,…,lm)。当实际值与预测值之间的向量夹角余弦越大时，表明预测值更加接近实际值，模型预测精度更高。当向量夹角余弦值达到1 时，表明预测值与实际值完全相等。根据上述描述及相关性质可得表达式：

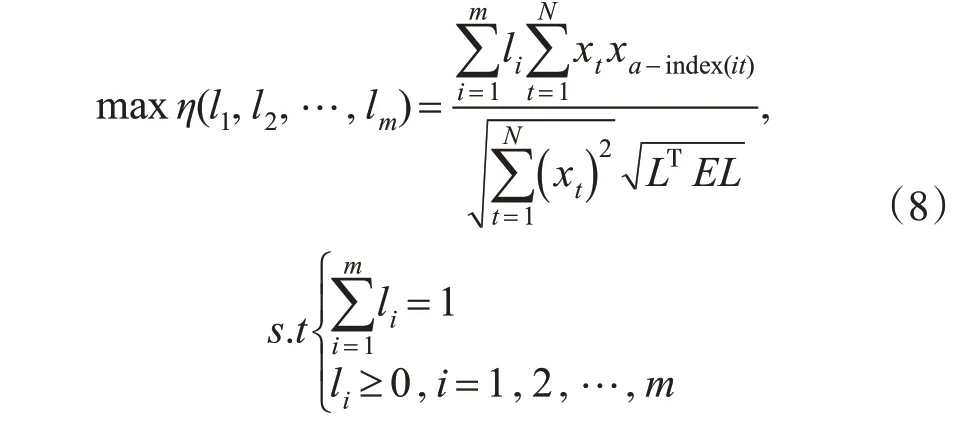
该模型是一个非线性规划模型，可利用相关规划软件解算各时刻单项模型的加权系数。

定义3 若组合预测值向量与实际值的向量夹角余弦η（l1,l2,…,lm)ηmin，则称组合预测为劣性组合预测；若ηmin≤η(l1,l2,…,lm)≤ηmax，则称之为非劣性组合预测；若η(l1,l2,…,lm)>ηmax，则称之为优性组合预测[8]。当且仅当组合模型的向量夹角余弦值最大，才是最优组合。

2 组合预测评价准则

模型预测效果的好坏通常需要建立相关的指标值来进行判定。本文采用5 种误差评价准则来评定模型的预测精度和准确度[9]，从而更加全面、准确地反映模型的精度高低。

1）均方误差（MSE）为：

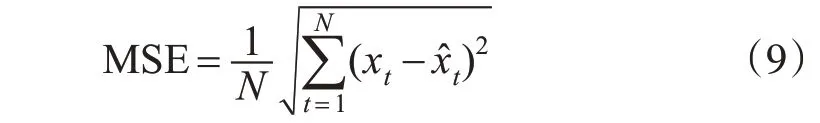
2）预测误差平方和（SSE）为：

3）平均绝对误差（MAE）为：

4）平均绝对百分比误差（MAPE）为：

5）均方百分比误差（MSPE）为：

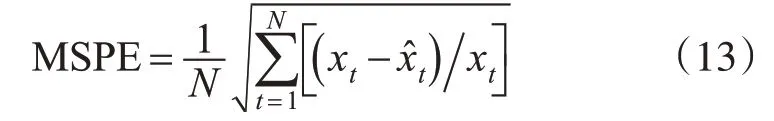
3 实例及分析

本文选取某市一条新建城市道路作为研究对象，其竣工时间为2019年6月。为掌握道路竣工后路基的沉降变化情况，根据相关规范及技术要求，每隔30 m在道路中间及两侧布设了沉降测钉，按国家二等水准规范要求进行施测，观测周期为15 d。选取2019 年6 月—2020 年2 月期间的19 期观测数据作为研究对象，其中前15期数据作为模型构建数据，后4期数据为预测对比数据，沉降量观测数据如表1所示。

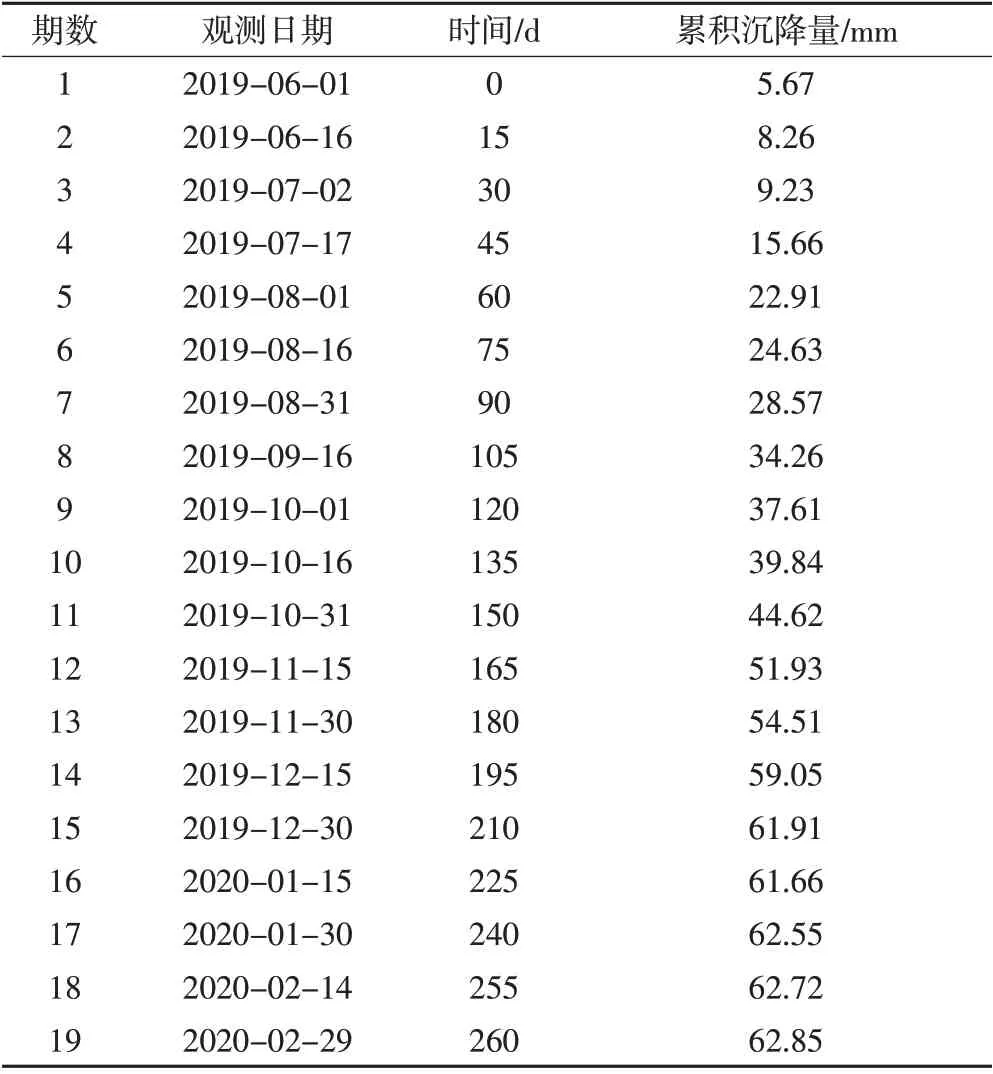
表1 软土路基累计沉降数据

首先，采用3种常用的软土路基沉降预测模型[10]对其沉降量进行预测分析，分别为灰色预测模型、双曲线模型、S 型预测模型，最后，采用式8 构建的组合模型对软土路基进行预测。

本文采用GM（1，1）模型对路基沉降量进行预测，利用观测所得到的前15期数据建立灰色模型，其中时间步长为=30，灰色模型如下式所示：

将原始观测数据进行累加后可建立微分方程，赋予一定权值后，解算得到（̂)=(0.253 2,17.129 6)。最终得原始数据预测模型为：X(0)(t+1)=16.770 5e-0.2532t。利用上述模型表达式可计算得出每期沉降量。

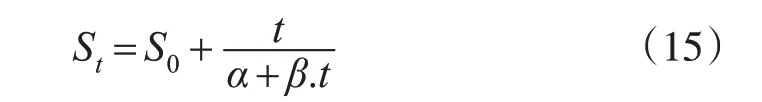
式中，S0为原始沉降量（t=0）；St为t时刻的沉降量；t为时间间隔；α、β为由实测值求得的系数。

根据观测数据和双曲线模型函数可得：St=34.48+t(1.255+0.03t)。由此预测沉降点各期的沉降量，结果如表2所示。

3） 本文选取S型曲线模型中的Mmrgan-Mer⁃cer-Flodin模型（MMF模型）作为预测模型，表达式为：

式中，yt为沉降量；L、a、b、r均为大于0的系数。

MMF 模型：由前15 期数据可得模型参数值为a=5.567、b=9 197.446 7、L=72、r=1.917 5 ，yt=（51 202.185 8+72t1.9175）/（9 197.446 7+t1.9175）。根据模型表达式，可得出监测点每期沉降量，根据精度定义表达式（1）可获得各模型的预测精度，预测结果如表2所示。

表2 单一模型拟合值与实际值对比

由单项预测方法的精度及相应的预测值组成二维数组（a1t,x1t），（a2t,x2t），…（amt,xmt），t=1,2,…19，根据式（2）可获得每期IGOWLA 算子的组合预测值。根据式（8）可获得组合模型的表达式为：

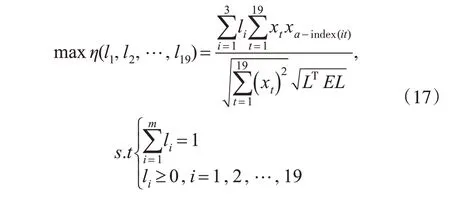
解算上述非线性规划函数，可得：l1=0.753 5，l2=0.143 5，l3=0.103 0。

分析对比表2 的数据可知，单项模型预测精度的持续性及稳定性较差，3 种模型的预测精度在不同时期各有高低，其在一定程度上均能反映实际沉降情况，但不够全面且可能存在错误信息。根据组合模型构建原则，实际应根据单项模型各时刻的拟合以及预测精度进行赋权，不可单依据模型种类赋权。根据式3，可得出各时刻组合预测值如下表3所示。

根据残差信息可获得3 种单一模型及组合模型的精度评价指标值，具体如表4 所示。根据各模型预测值绘制预测曲线图如图1所示。

由表1、表2、表3的模型预测数据可知，相对于3 种单项预测模型，组合模型的预测残差值最小，精度值最高且更接近于实际观测值。由表4 的数据可知，组合模型的5 种精度评价值均最小，从而可判定组合模型的预测精度更高，预测精度的稳定性及持续性更强且预测性能更加良好。从图1 的预测曲线图可知，组合模型相对于单一模型，其曲线变化趋势更加吻合实际情况。

图1 模型预测曲线图

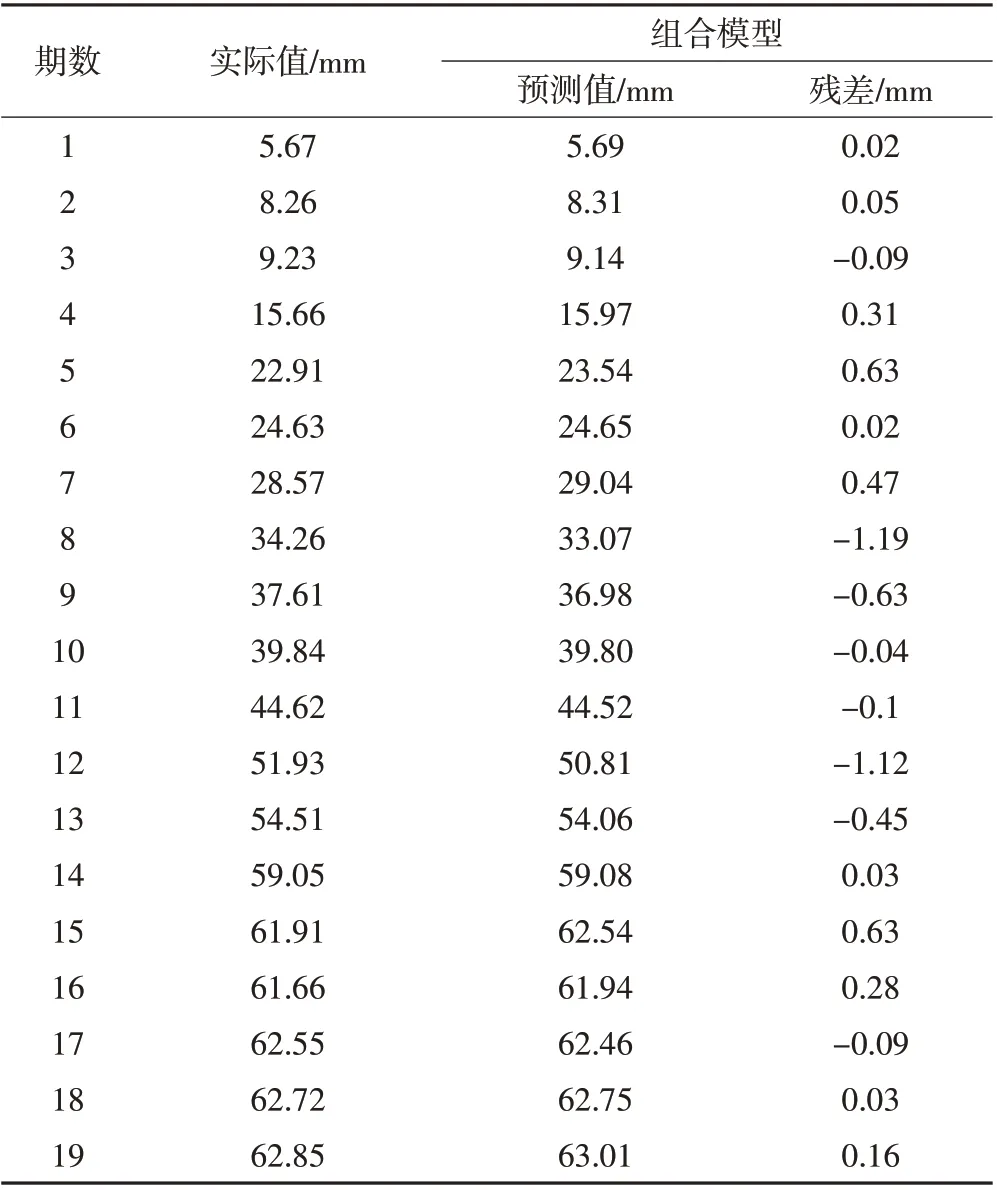
表3 组合预测值

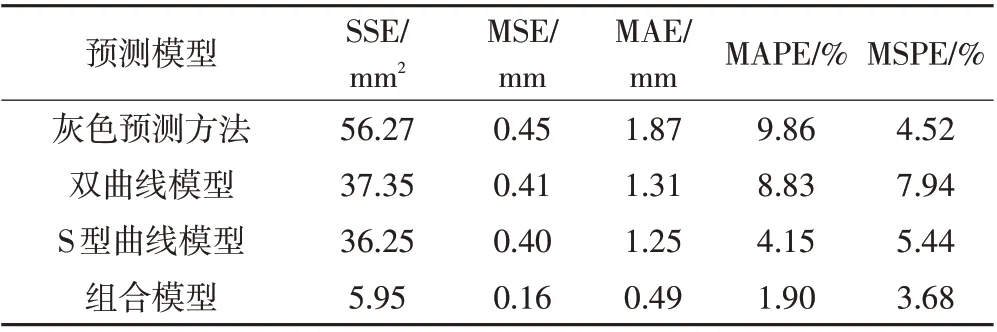
表4 模型拟合精度评价指标

计算各模型的向量夹角余弦值分别为：η灰色=0.994 82，η双=0.995 45，ηS=0.996 13，η组合=0.998 15。由此可知，组合模型的向量夹角余弦值最大，为优性组合模型。

根据预测连续性原则，利用建模的观测数据越多，其获得的预测模型精度越高，越能反映实际情况，即利用16期观测数据所建立的预测模型的精度要高于15 期观测数据所建立的预测模型，同理，利用17期观测数据建立的预测模型精度更高，预测更准确。

4 结 论

1）各单项预测方法均包含一定的有效信息，在某时刻能较好地反映实际变化情况，但往往其精度不具有持续性，个别时段可能存在错误信息。本文提出的组合模型能充分、利用各单项预测模型的有效信息，避免错误信息的影响，提高数据预测精度，由预测结果可知组合模型在路面沉降数据预测中得到了良好的应用，可以为类似数据预测提供借鉴。

2）本文通过对组合模型相关理论的阐述，引入了IGQWLA 算子及向量夹角余弦的定义，并提出了基于向量夹角余弦的组合模型构建方法及优性组合判定方法。实例证明，该方法切实可行，能有效提高预测数据的精度，可广泛应用于相关工程项目的数据处理中。

3）本文提出的模型精度计算方法科学合理，能准确地反映模型预测效果的好坏，是判定精度高低的重要指标。