MATLAB遗传算法在函数优化问题中的应用
2023-01-03刘光亚
刘光亚
应用研究
MATLAB遗传算法在函数优化问题中的应用
刘光亚
(武汉东湖学院机电学院,武汉 430212)
本文介绍了遗传算法理论及运算流程,运用MATLAB语言进行了程序设计。结合典型的三角测试函数,在MATLAB 环境下有效地解决了用遗传算法求解函数优化问题,验证了 MATLAB 遗传算法在函数优化中应用的有效性和灵活性。
遗传算法 MATLAB 函数优化 有效性
0 引言
20世纪70年代,美国密执安大学的 Holland 教授[1]提出了遗传算法,它包含了进化和自然选择原理,它借鉴了达尔文的进化论和孟尔德的遗传学,模仿了自然界的生物进化机制,并发展成为一种随机全局搜索和优化方法,是一种全局、并行、高效的搜索方法[2]。它能在搜索过程中自主获取和积累有关搜索空间的信息,并自适应地控制搜索过程以求得最优解。遗传算法提供了一种求解非线性、多模型、多目标等复杂系统优化问题的通用框架,它不依赖于问题所属的具体领域,已广泛应用于函数优化、自动控制、图像处理、机器学习、人工生命与智能等领域[3]。
MATLAB是一种用于算法开发、数据可视化、数据分析及数值计算的高级技术计算语言和交互式环境,具有计算功能强大、图形展示功能强大、工具箱功能强大和帮助功能完整等特点。MATLAB遗传算法提供了对各种优化问题的一个完整的解决方案[4]。它具有函数表达简洁、遗传操作灵活、可任意选择多种编码方式和优化算子、算法参数设置自由等特点而受到用户的青睐,并为应用和研究遗传算法提供了稳定可靠、结构灵活、可扩展的开发平台。
函数优化问题是遗传算法的经典应用领域,也是对遗传算法进行性能评价的常用算例[5]。
1 遗传算法原理与运算流程
在自然进化的过程中,生物通过遗传与变异来适应外部环境。这就意味着,只有那些拥有更加优良特性和更适应自然环境的生物才能生存与繁衍;同时,那些没有优良特性的生物体最终将会消亡。这也就是所谓的“适者生存”。遗传算法模拟了上述的自然进化现象,它将搜索空间映射到遗传空间,也就是说将每个有可能的解经基因编码成一个染色体。
遗传算法模拟了自然选择和遗传中发生的复制、交叉和变异等现象,随机产生一初始种群,通过复制、交叉、变异等操作,产生适应度更高的个体,使群体进行到搜索空间中越来越好的区域,如此一代代进化,最后收敛到一群适应度最好的个体中,进而求得问题的最优解。
遗传算法流程可用图1来描述:

图1 遗传算法流程图
2 应用实例
示例函数采用典型的如下三角测试函数:
求其函数于自变量x在定义域中的最大值,遗传算法优化程序[6]如下:
Function optvalue=opt(n, maxgen, xmin, xmax, pc_min, pc_max,pm_min, pm_max, l) % n-染色体规模;maxgen-最大进化代数;xmin-自变量最小值;xmax-自变量最大值;pc_min-最小交叉概率;pc_max-最大交叉概率;pm_min-最小突变概率; pm_max-最大突变概率;l-二进制码串长度;
gen=1;group=round(rand(n,l));
while gen<=maxgen % 判断终止条件
x=decode(group,xmin,xmax,l);
fit=x.^2.*sin(2*x)+2*cos(5*x)+x; % 求适应度值
for i=1:n % 适应度值预处理
if fit(i)<0
fit(i)=0;
end
end
prob1=fit/sum(fit);prob1=cumsum(prob1);
prob2=sort(rand(n,1)); i=1;j=1;
while i<=n %利用轮盘赌选择法来进行选择操作
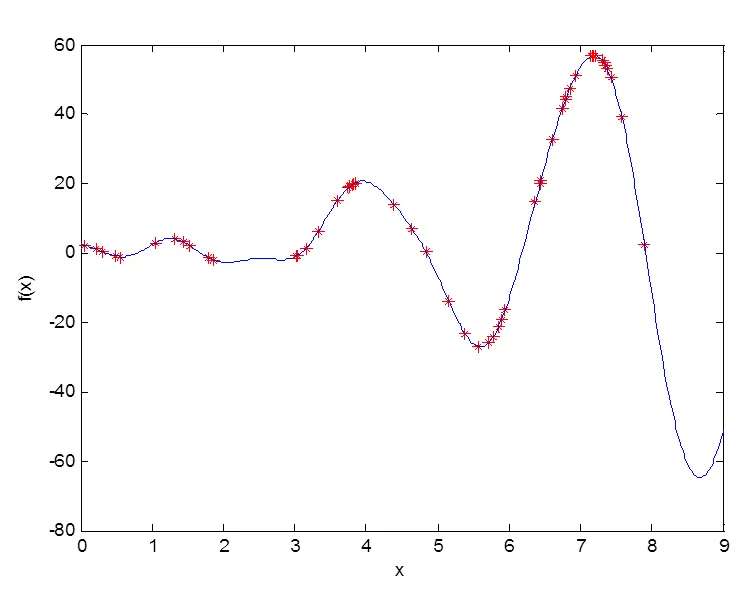
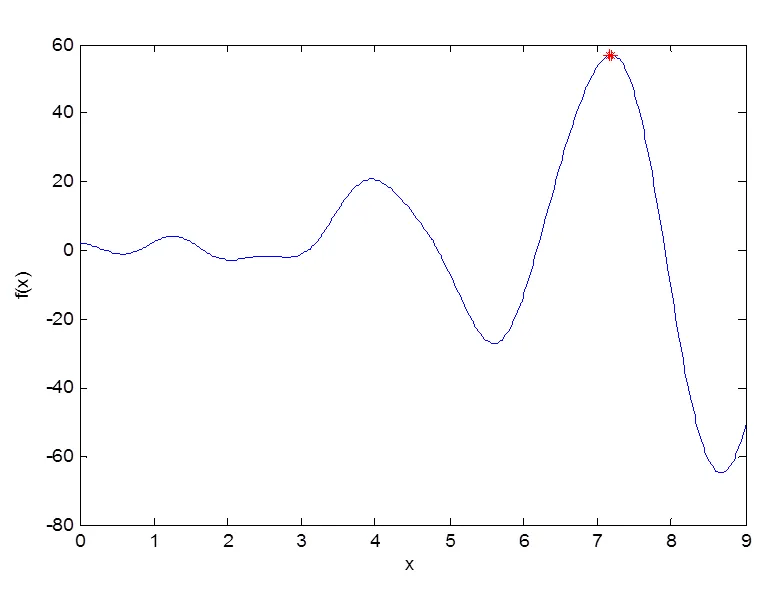
if prob2(i) newgroup(i,:)=group(j,:); i=i+1; else j=j+1; end end group=newgroup; x=decode(group,xmin,xmax,l); fit=x.^2.*sin(2*x)+2*cos(5*x)+x; avgfit=mean(fit); for i=1:2:n-1 %随机生成交叉点,并进行交叉操作 a=[fit(i) fit(i+1)]; if max(a)>avgfit pc=pc_max-(pc_max-pc_min)*gen/maxgen; else pc=pc_max; end if rand cross=round(rand*l)+1; if cross>l cross=cross-1; end newgroup(i,:)=[group(i,1:cross) ; group(i+1,cross+1:end)]; newgroup(i+1,:)=[group(i+1,1:cross); group(i,cross+1:end)]; x2=decode(newgroup(i:i+1,:),xmin,xmax,l); fit2=x2.^2.*sin(2*x2)+2*cos(5*x2)+x2; for j=0:1 if fit(i+j)>=fit2(j+1) newgroup(i+j,:)=group(i+j,:); end end else newgroup(i,:)=group(i,:); newgroup(i+1,:)=group(i+1,:); end end group=newgroup; for i=1:n % 随机生成变异点,并进行变异操作 x3=decode(group,xmin,xmax,l); fit3=x3.^2.*sin(2*x3)+2*cos(5*x3)+x3; avgfit3=mean(fit3); if fit3(i)>avgfit3 pm=pm_max-(pm_max-pm_min)*gen/maxgen; else pm=pm_min; end if rand mutation=round(rand*l)+1; if mutation>l mutation=mutation-1; end newgroup(i,:)=group(i,:); if newgroup(i,mutation)==0 newgroup(i,mutation)=1; else newgroup(i,mutation)=0; end x4=decode(newgroup(i,:),xmin,xmax,l); fit4=x4.^2.*sin(2*x4)+2*cos(5*x4)+x4; if fit3(i)>fit4 newgroup(i,:)=group(i,:); end else newgroup(i,:)=group(i,:); end end x=decode(newgroup,xmin,xmax,l); fit=x.^2.*sin(2*x)+2*cos(5*x)+x; [gmax(gen) index]=max(fit);r(gen)=x(index); meanvalue=mean(fit);meanfit(gen)=meanvalue; group=newgroup;gen=gen+1; end figure(1);fplot('x.^2.*sin(2*x)+2*cos(5*x)+x',[xmin,xmax]); hold on; plot(r,gmax,'r*');xlabel('x');ylabel('f(x)') figure(2); plot(gmax); hold on; plot(meanfit,'r:'); xlabel('generations');ylabel('f(x)');hold off; [gmax index]=max(gmax); optvalue=[r(index) gmax]; Function x=decode(group, xmin, xmax, l) %子函数实现二进制-十进制的解码操作 group=fliplr(group);s=size(group); a=0:1:l-1;a=ones(s(1),1)*a; x1=sum((group.*2.^a)'); x=xmin+(xmax-xmin)*x1./2^l-1; 按照上述算法,令n=50,maxgen=80,x_min=0,x_max=9,pc_min=0.1,pc_max=0.9,pm_min=0.01,pm_max=0.4,l=22;图2代表了初始种群的位置分布;图3指出了经过80次迭代后的最终寻优结果;图4说明了随着代数的增长,最优值与平均函数值的变化趋势;输出结果为: X=7.1928,y=57.0137. 遗传算法作为一种快速、简单、容错性强的算法,是一类可应用于复杂系统优化计算的鲁棒搜索算法,相较于传统优化算法,它有如下特点: 1)遗传算法不是从一点出发沿一条直线寻优,而是同时在整个解空间进行寻优操作,具备全局寻优能力。 2)遗传算法直接作用于变量的编码上,而非变量本身。通过编码操作,可以直接对结构对象进行操作。 3)遗传算法对搜索空间没有任何特殊要求,只以变量的编码作为操作对象,无需导数等其它辅助信息,可处理无数值概念或者很难有数值概念的优化问题。 图2 染色体的初始位置 4)本文实验结果验证了 MATLAB 遗传算法能有效、灵活地求解复杂函数的优化问题,而且所求解能达到或以相当高的精度逼近最优解。 图3 染色体的最终位置 图4 最优、平均函数值变化趋势 [1] Holland J H. Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence[M]. Ann Arbor: University of Michigan Press, 1975. [2] Rodés J P, Pérez-Gracia V, Martínez-Reguero A.Evaluation of the GPR frequency spectra in asphalt pavement assessment[J]. Constr Build Mater, 2015, 96: 181-188. [3] 周勇, 胡中功. 改进的快速遗传算法在函数优化中的应用[J]. 现代电子技术, 2018, 41(17): 153-157. [4] 殷铭, 张兴华, 戴先中. 基于MATLAB的遗传算法实现[J]. 电子技术应用, 2000, 26(1): 9-11. [5] 曹岩. MATLAB R2008数学和控制实例教程[M]. 北京: 化学工业出版社, 2009. [6] 由睿鹏.计算机网络优化设计中遗传算法的原理及应用[J]. 电子技术与软件工程, 2020(20): 14-15. [7] 李晓叶, 张京丽, 于妍. 动态图表展现遗传算法基本原理[J]. 电脑编程技巧与维护, 2017(12): 80-81, 94. [8] 万勇, 万莉, 戴永寿. 基于C与MATLAB混合编程的管道缺陷类型识别实验系统软件开发[J]. 实验技术与管理, 2020, 37(5): 52-57. Application of MATLAB genetic algorithm in the function optimization problem Liu Yaguang (School of Mechanical and Electronic, Wuhan Donghu University, Wuhan 430212, China) TP18 A 1003-4862(2022)12-0050-04 2022-08-09 国家自然科学基金资助项目(12101468、61573002) 刘光亚(1959-),男,工学博士,研究员级高工、教授(二级)。研究方向:检测技术及自动化系统,动力(核)与电气工程。E-mail:648069538@qq.com3 仿真结果
4 结语