基于Simulink的EV节能车“加速-滑行”的能耗仿真分析

李永耀,岑加俊,黄泽豪,戴靖,陈宇,王丽

广州城市理工学院，广东广州 510800

0 引言

根据汽车环保马拉松大赛竞赛规则[1-2]，电动原型车的赛事由各车队自行配备电池，赛方通过在电池输出端安装焦耳计来测定车辆在行驶过程中能量的损耗值，并且比赛单圈有最低平均时速25 km/h的要求，续航里程长的车辆为节能竞技比赛的优胜者。在备赛过程中，EV节能车结构初步完成后，需要根据路况和车体运行情况，不断调整驾驶策略，让车辆用更小的电量行驶更远的距离[3]，以实现较优良的能耗性能，并进一步实现大赛节能减排的宗旨和提高环保意识，同时也提高参赛者的实践动手能力和解决问题的能力。

本文通过Simulink建立了驾驶策略模型，并结合行驶道路的坡度信息，以“加速-滑行”的驾驶策略进行行驶能耗仿真分析。分析表明节能车在“加速-滑行”的特定行驶策略下，其平均时速满足要求，续航能力较好，所探讨的“加速-滑行”的驾驶策略行驶能耗仿真分析对于降低车辆试验的时间成本和经济成本产生影响。

1 基于Simulink的EV节能车能耗仿真总体框架

EV节能车整车结构由外壳、车架及电动机三大部分组成[4-6]，搭建的EV节能车能耗仿真系统由驾驶策略模型、电机模型、传动系统模型、车辆纵向动力学模型、道路模型和结果查看模型构成并进行有机关联。因测试路段长度为3.26 km，在仿真中仅对节能车进行单圈能耗仿真[7-8]，因此当车辆行程达到3.26 km，节能车能耗仿真停止运行。Simulink仿真模型总体框架如图1所示。

图1 Simulink仿真模型总体框架

2 驾驶策略模型的建立

由于汽车环保马拉松大赛赛场存在坡度和弯道，且有最低电量输出和平均时速25 km/h的要求。因此，要实现以上基本目标，车手在无紧急情况下不采取车辆制动，这就要求车手必须具备丰富的赛事经验。通常做法是：EV节能车通过先加速到某一时速，然后断电让车辆滑行，当车辆滑行降到特定时速后，再进行加速，以此“加速-滑行”往复进行来完成整场比赛。

驾驶策略模型是在Simulink下通过Stateflow来制定的驾驶方式。如图2建立的驾驶策略模型所示，通过输入车速信息和弯道曲率信息来决定电门开度，即PWM占空比。

图2 驾驶策略Simulink模型

图3为驾驶策略Stateflow模型。该模型是状态与动作的执行和转换，分别有3种状态：power_on，power_on1，power_off1；两种动作：K=60，K=0；两个条件判断参数：v和R。考虑到电池放电倍率、电机输出扭矩克服道路中最大的坡度阻力等因素，设置默认状态(power_on)下，此时执行动作是K=60，代表控制电机的电门旋钮处于PWM为60%的位置；当车速达到状态转移条件(v≥28 km/h)时，状态切换至“power_on1”，此时PWM仍是60%；当车速v增加到34 km/h时或者车辆行驶在曲率半径阈值位置时，进入状态“power_off1”，即PWM为0%；当车速低于20 km/h，重新回到状态“power_on1”，PWM也回到60%；当车速不大于22 km/h，回到默认状态“power_on”。按照此方式不断循环。

图3 驾驶策略Stateflow模型

3 道路模型的建立

仿真模型中，对EV节能赛车行驶在一段环形的道路进行能耗分析。采集道路的经度、纬度和海拔高度的一系列连续离散数据点后，通过MATLAB进行数据预处理，转化为笛卡尔坐标系的数据点。通过公式(1)和公式(2)分别进行坡度值和曲率半径进行求解。

(1)

(2)

式中：xk、yk、hk分别为该路段第k点在笛卡尔坐标系的x轴、y轴、z轴坐标的对应值;θ为道路与水平地面的夹角;r为道路的曲率半径。

仿真所用的道路三维形状如图4所示，该道路的求解结果如图5所示。因车辆在弯道处进行加速，设定r=20 m为曲率半径阈值。曲率半径小于r时，该位置给予标记R=0，代表此位置禁止启动电机，否则给予标记R=1，表示允许电机启动。在Simulink仿真模型中，通过车辆行驶所在的位置来查询道路信息，如图6所示。采用一维查表模块，通过车辆当前位置查询当前坡度值。

图4 仿真所用的道路三维形状

图5 仿真路段坡度、曲率半径及海拔高度的变化曲线

图6 仿真路段坡度信息模型

4 车辆纵向动力学模型的建立

以当前最新的EV节能车为载体建立车辆纵向行驶方程为：

(3)

(4)

(5)

式中：η为传动效率;a为车辆纵向加速度;vk+1为k+1时刻车辆速度值;vk为k时刻车辆速度值;Sk+1为车辆k+1时刻的行程;Sk为车辆k时刻的行程。

EV节能车的动力学模型参数见表1。

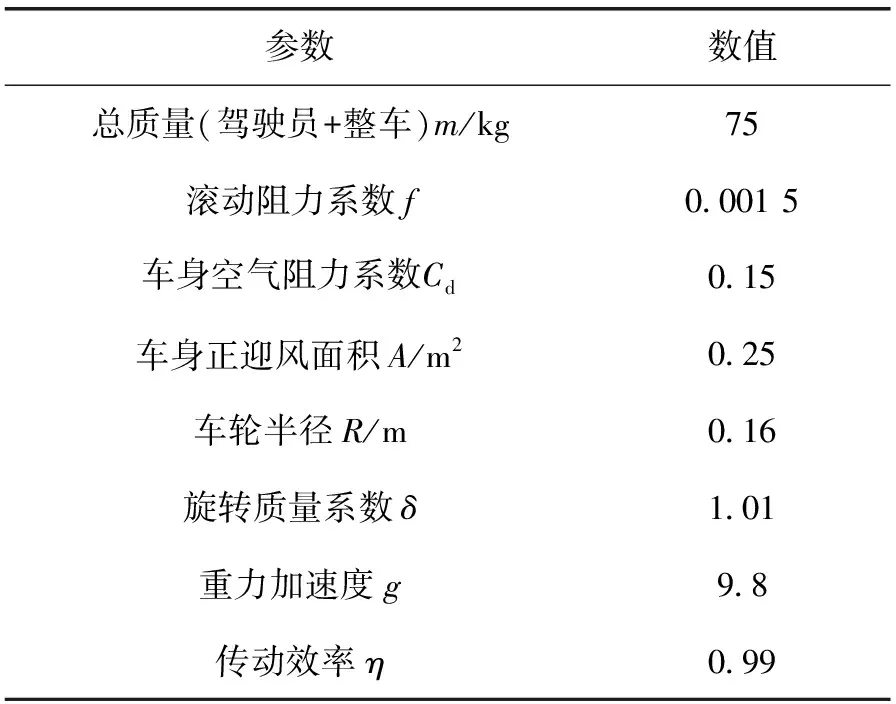
表1 EV节能车的动力学模型参数

在仿真过程中，以加速度a为切入对象，通过车辆当前速度、车辆所处位置坡度值和车辆此刻电机输出扭矩值动态信号，对加速度a积分，可求出速度和路程。行驶阻力模型如图7所示，车辆纵向动力学模型如图8所示。

图7 行驶阻力模型

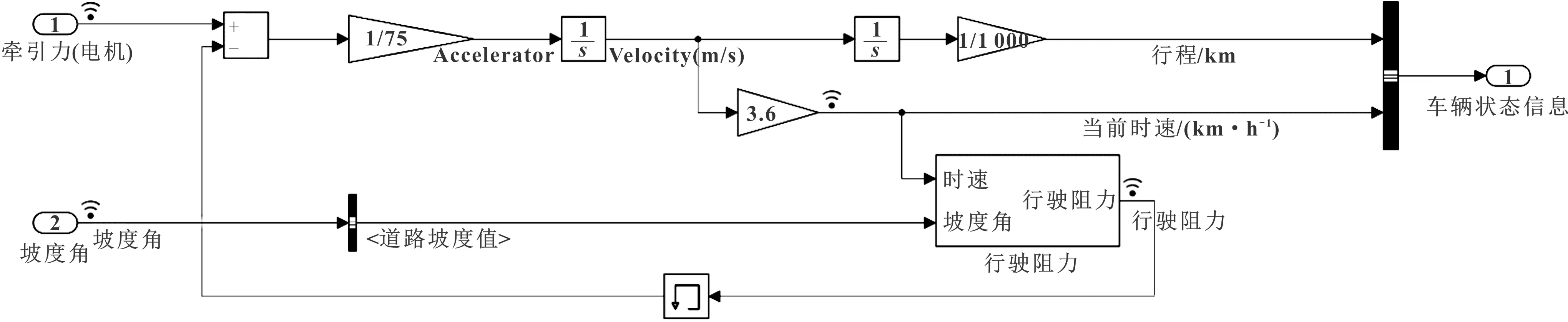
图8 车辆纵向动力学模型

5 电机模型的建立

本文的EV节能车电动机模块采用的是无刷直流电机，在Simulink仿真模型中，电机效率可以通过查表方式来确定，其效率可以表示为方程(6)，电机的输出扭矩可以通过方程(7)来确定，电机输出功率可以表示为方程(8)。电机模型如图9所示。

图9 电机模型

输入信号是电门开度和车速，输出信号有电机工作效率、电机输出扭矩和电机输出功率。

ηm=f(Tt,n)

(6)

(7)

(8)

式中：ηm为电机输出效率;n为电机转速;E为电门开度;Pm为电机输出功率;N为电机基速;Tt为电机实时输出扭矩。

6 仿真结果

本文模拟了驾驶员在一段测试道路上以“加速-滑行”的驾驶方式下的能耗损失。但存在一定的理想条件，例如，车辆在转弯过程中能量的损耗假设为0，赛道的环境风速假设为0，车手在操控电门转把时能瞬间将转把转到一定的角度。为了提高仿真数据的精确度，在Simulink仿真求解器中选择定步长为0.01来进行仿真运算。两个重要仿真指标是：节能效应为874.1 km/kWh，平均时速为27.13 km/h。即在该测试路段下按照上述制定的驾驶策略进行驾驶，其节能指标是一度电能行驶874.1 km，而其平均时速为27.1 km/h。

图10为车速仿真结果，反映了车手在赛道各位置的车速大小，明显呈现出“加速-滑行”的驾驶风格，平均车速达到了27 km/h,符合赛事最低平均车速的要求。

图10 车速仿真结果

根据图11和图12的车速曲线与相对海拔高度和电机输出功率分布的关系，可知在整段道路上，不同的海拔高度和电机输出功率的分配给车速带来了影响，而制定更具有节能效应的驾驶策略，往往需要根据道路的坡度、车速来调整电机在整段道路的功率分配。

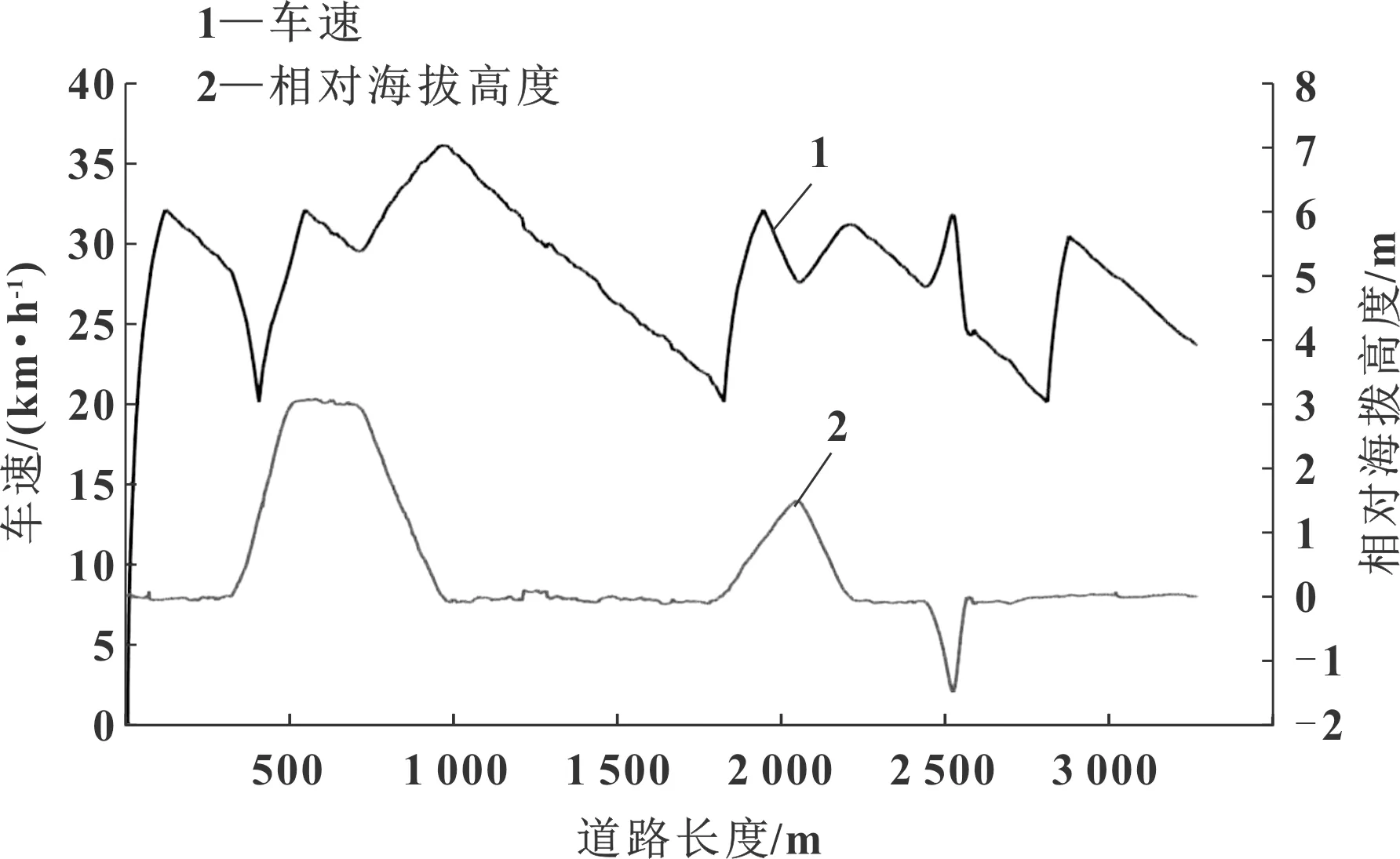
图11 车速曲线与相对海拔高度的关系

图12 车速曲线与电机输出功率分布的关系

图13为驾驶员操控的电门开度值，图14为电机工作效率仿真结果。由图可见：电机工作期间的效率基本大于80%，车速具有较明显的加速再减速的循环特征；电机工作时间占车辆行驶总时间较少，证明节能赛车具备低滚阻、低风阻的优点；受到起伏不平的道路坡度角影响，节能车会在某一段距离速度超过35 km/h，原因是在长距离的下坡路段，节能车不断滑行加速。

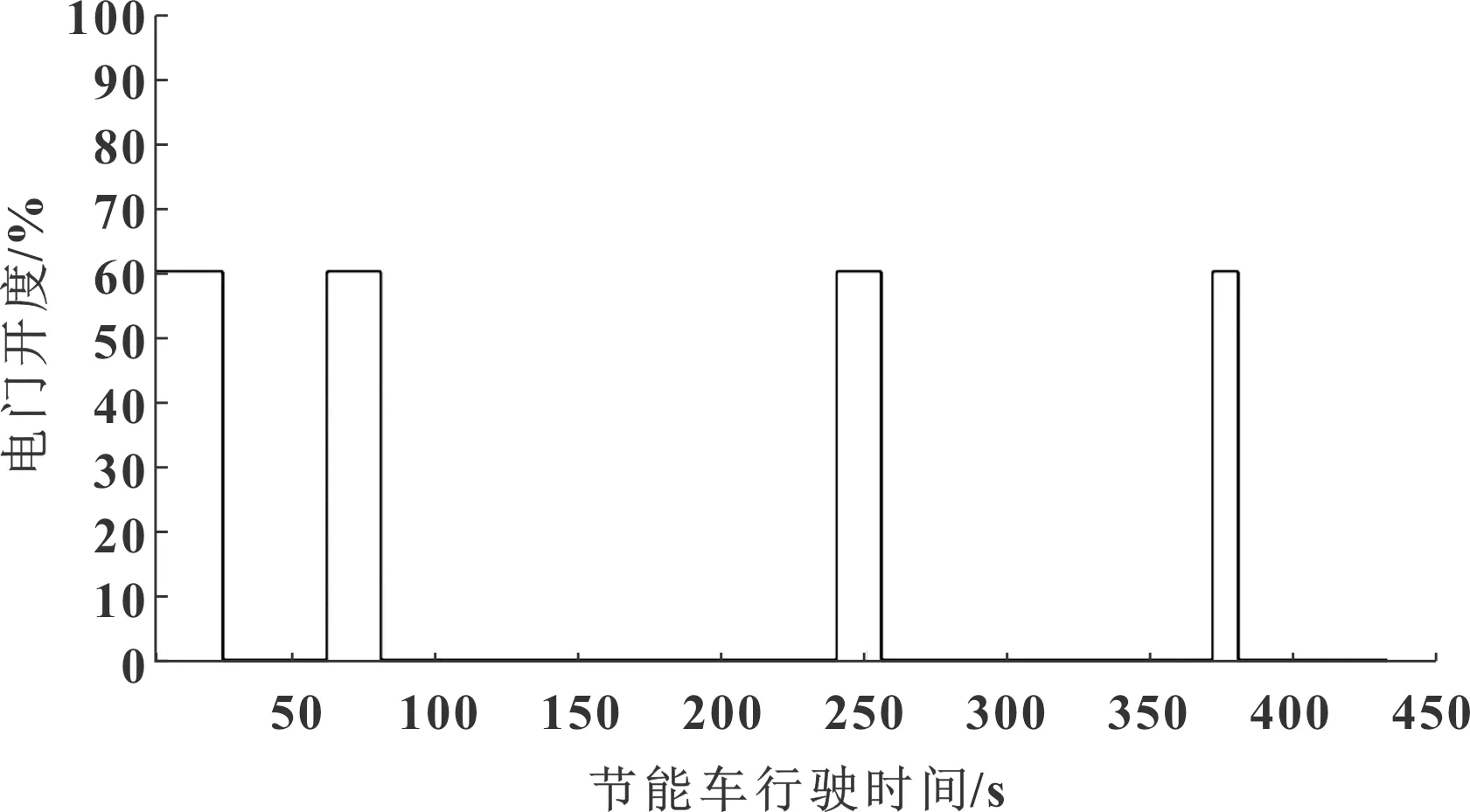
图13 驾驶员操控的电门开度值

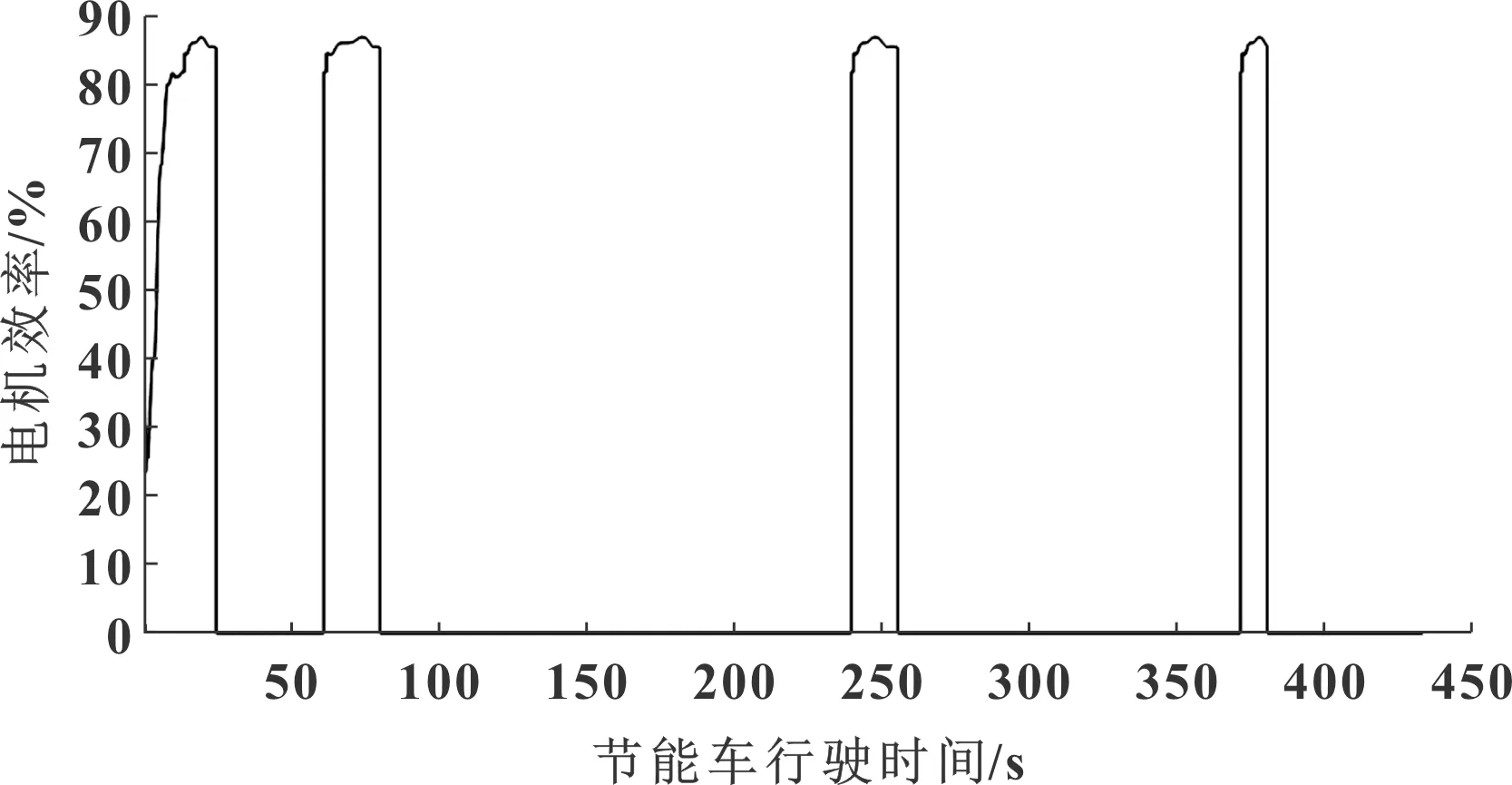
图14 电机工作效率仿真结果

在如图15所示的结果查看模型中，添加Display模块可直接观察数据。由图可以看出，按照仿真设定的条件，节能车在该路段的平均行驶车速为26.74 km/h，每度电能行驶698.3 km;则在该路段按照本文设定的驾驶策略行驶，能达到最低时速25 km/h的条件，并且能在有限的电量下跑出更远的距离。

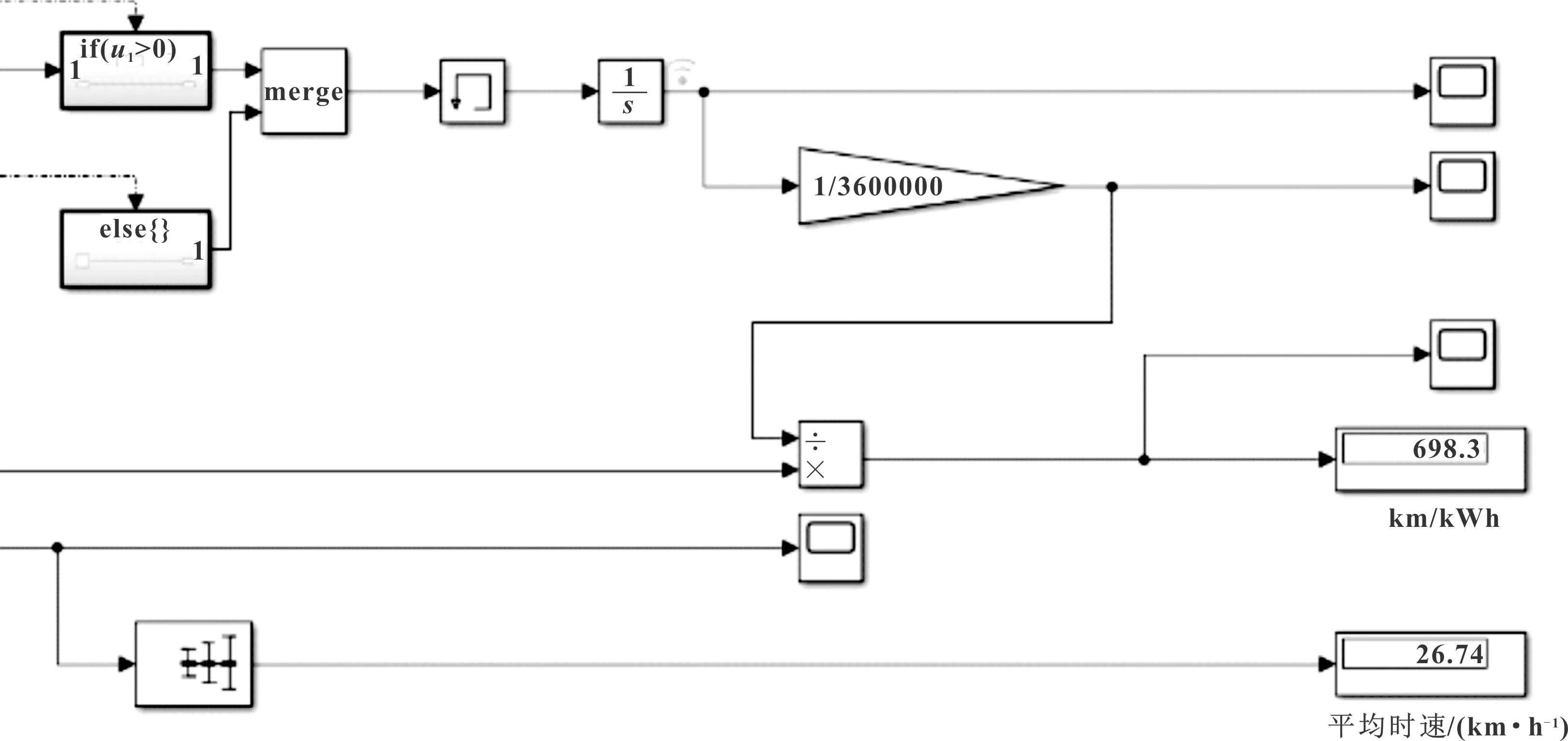
图15 结果查看模型

7 结束语

根据目前在中国举办的壳牌汽车环保马拉松大赛和中国节能竞技大赛的电动组别赛事规则，最小能耗、最远续航里程的车辆为节能竞技比赛的优胜者。通过Simulink搭建EV节能车能耗仿真总体框架和车辆纵向动力学模型，建立了驾驶策略模型;结合行驶道路的坡度和转弯半径信息，以“加速-滑行”的驾驶策略进行行驶能耗分析。通过仿真结果可初步检验节能车在“加速-滑行”的特定行驶策略下，其平均时速达到赛事要求，续航能力较好。