浅谈高考数学考试中的不等式
2023-01-03席雪梅
席雪梅
(合肥体育运动学校 安徽合肥 230031)
不等式在数学中有着非常重要的地位,发挥着重要的作用。不等式在高考中一直都是热门的话题,在往年的高考中占分比例较大,考查的形式多样,运用到的方法也灵活多变。平时我们比较关注等式问题而容易忽视不等式的问题,殊不知不等式的研究涉及面更广、难度相对比较大,但却有利于学生独立思维能力的提高;不等式题目出现的形式多种多样,其解题方法的难易也有不同的差距。为了更好地掌握中学数学及高考数学题中不等式的内容、考点和解题技巧等,本文结合有关不等式的教材和研究者们的研究成果,对中学数学中不等式类题目进行研究,从而找出解题的技巧和规律,为学生的“学”和教师的“教”提供一定的帮助。
一、不等式的基本概念
数量关系可分为等量关系和不等量关系。不等量关系和等量关系是非常重要的研究对象,是解决数学问题的关键。下面描述的是不等式的内容和它本身的一些问题,其中有不等式的基本概念和中学中常见的不等式。
不等式是指不等量关系的式子,它分为严格不等式和非严格不等式,用数学符号“>”“<”连接的不等式称为严格不等式,用“≥”“≤”连接的不等式称为非严格不等式,也称为广义不等式。总的来说,用“≠”“>”“<”“≥”“≤”这些数学符号连接起来的式子,叫作不等式。
二、中学数学中的不等式试题研究
(一)不等式试题的统计与分析
我们知道中学数学中的不等式主要集中在高中阶段,而高中教育的最终目标就是高考,高考标准化是由制定高考的大纲、试题的编拟和试卷的合成的标准化、考试实施的标准化、评分的标准化、分数转化的标准化这五个部分构成。而在高考中,不等式又有着举足轻重的地位,被很多的研究者作为研究对象进行研究。例如,《高中数学不等式高考试题分析与教学策略研究》的作者张惠淑对近几年来高考中的不等式内容进行分析和总结,并对不等式教学提出了相应的教学目标。
1.不等式内容的考点统计与分析
对于不等式试题的统计,笔者从近几年的高考入手,并加以分析。虽然不等式涉及的知识点很广,但是高考对不等式的考查还是有着一定范围的。根据高中教材和高考的说明,笔者从不等式性质的应用、解不等式、不等式中的线性规划、求最值和取值范围这几个方面,来统计2017年到2020年这四年来不等式在高考中出现的频率。如表1所示。
从表格中可以看出,各个地方近四年来高考涉及的不等式知识频率较高的是最值问题和解不等式。其中全国Ⅰ卷中,解不等式知识出现的频率最高,达到9次;全国Ⅱ卷中涉及不等式知识点频率最高的是求最值问题,达到8次;全国Ⅲ卷中涉及不等式知识出现频率最高的还是求最值问题;就北京卷而言,近四年来高考中涉及的不等式知识点的频率比较均匀。以上是各个地方近四年来高考中涉及不等式知识出现的频率分析,据此我们可以清楚地了解到各个地方对于不等式的考查更侧重于哪个知识模块。
2.不等式出现的题型统计与分析
在数学的高考试卷中除了江苏卷没有选择题,其他的数学高考卷中的题型分为选择题、填空题和解答题。笔者以2020年各个地方数学高考试卷中涉及不等式出题的类型及关于不等式出题数在总题量中占的比值进行统计。如表2所示。
从2020年高考数学不等式相关试题出题类型统计表中可以看出,不等式占总题量的比值都在30%以上,其中最高的是北京卷和江苏卷占到50%,天津卷占到40%,全国Ⅰ、Ⅱ、Ⅲ卷的比值在30%以上。2020年关于不等式的出题量各省都是大于或等于7题,江苏卷有11题,天津卷和北京卷都有10题,全国Ⅰ、Ⅱ、Ⅲ卷分别有7题、9题、9题。从题型数量上看填空题少于解答题少于选择题,而天津卷中解答题与填空题都有5题不等式的题目。
(二)中学数学中的不等式试题类型及解法
根据对近几年来全国各个地方高考数学涉及的不等式知识中了解到,高考数学主要是从解不等式、不等式性质的应用、不等式中的线性规划、求最值和求取值范围这五个方面来考查,下面将对这五个方面和解题经常用的方法进行研究。
1.解不等式问题
解不等式经常会用到几何、函数、集合、导数等知识点,涉及的不等式有一元一次和一元二次不等式、高次不等式和指数不等式等。根据题目要求可以直接解出不等式或间接解不等式。一般情况下,这个问题会以选择题和填空题的形式出现,但也会以解答题的形式出现。
(1)直接解不等式问题
(2020年高考全国Ⅰ卷)设集合A={x|x2-4≤0},B={x|2x+a≤0}且A∩B={x|-2≤x≤1}则a=( )。
A.-4
B.-2
C.2
D.4
分析:先求出集合A、B,再根据数轴上交集的结果得到关于a的方程,最后解出方程就可以得到a的值了。
(2)间接解不等式问题
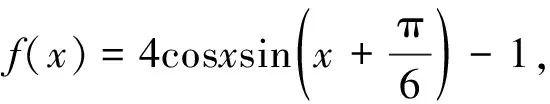
分析:这道题涉及高中必修4里的三角函数知识,解此题要熟悉三角函数的和角公式,通过降幂变为我们熟悉的正弦函数,最后求出f(x)在区间上的最值。
2.不等式性质的应用问题及解析
利用不等式性质来比较大小在利用不等式性质来比较大小的题型中,很多时候会涉及三角函数、指数函数、对数函数等知识,因此解决这类问题,就要对这些知识点牢固掌握并能灵活地运用。如下列题型。
(2020年数学高考全国Ⅰ卷)若2a+log2a=4b+2log4b,则( )
A.a>2bB.a<2b
C.a>b2D.a 3.线性规划问题 线性规划问题差不多每一年的高考都会考,其主要是对最值问题的考查,出题的形式也是有选择题和填空题、解答题,主要以选择题与填空题的形式出现。线性规划问题要根据图形求出最值,很多时候它的题型都差不多,但也有一些与常规题型不同的题,这时解题就需要较强的迁移能力。 分析:根据题目中的条件作出约束条件的图形,并画出可行域,根据目标函数找出合适的坐标,求出最大值。 4.不等式最值问题 求最值是比较常见的问题,也经常运用到基本不等式、柯西不等式等知识,并结合圆锥曲线与直线的临界问题出现。 分析:这道题是利用均值不等式来求最值的。常用的求最值的方法有分离法、换元法、直接法、“1”的替换法等,需根据题型选用。例如对于多元不等式问题,比较简便的方法就是换元,把多元的问题转化为一元的问题,从而解题。 5.不等式取值范围问题 求不等式的取值范围也是常考的一个知识点,主要考查不等式与函数、向量之间的关系。近几年来的高考数学中经常以选择题、填空题的形式出现。 A.(-2,2) B.(-∞,-2)∪(2,+∞) C.(-∞,-2]∪[2,+∞) D.[-2,2] 不等式在数学中占着重要的地位,它涉及的知识体系非常广,在庞大的数学体系中有着不可缺少的地位。本文主要以比较有代表性的高考不等式试题作为统计对象,进行研究。 在统计研究中发现高考的选择题、填空题、解答题(除江苏卷没有选择题外)里都有涉及不等式的知识,在题量上解答题多于选择题多于填空题,并且每一年题型的变化情况相差不大,其题量大多占总题量的百分之三十以上。 在高考中,有关不等式的试题有五种类型:解不等式问题、不等式性质的应用、不等式中的线性规划、求最值和求取值范围。通过对这些题型的分析发现,它们的解决涉及的知识点很多,集合、函数、导数、圆锥曲线等知识都有涉及,或者是解决集合、函数、导数、圆锥曲线等知识问题时,不等式是解决问题的关键。而直接考查不等式的问题却比较少。 在解不等式问题时,如果只停留在找出答案是远远不够的,要灵活运用所学知识,多方面思考问题,找到突破点,从而解决问题。在面对形式各异的题型中如果遇到无理不等式时,要把其转变成熟悉的有理不等式来求解;遇到有理不等式的分式不等式时,要把其转变成容易求解的整式不等式;如果是整式不等式中的高次不等式,就把其转变成低次不等式。并且要学会用数形结合的方式来分析解题,这在解决不等式的线性规划问题中经常用到。 教学不等式时,要从教材出发,引导学生掌握好基础知识,再通过不等式的练习提高解题能力。 在不等式的教学中,要教会学生用数学的眼光看问题,用数学的思想解决问题,要重视学生能力的培养,发展学生的数学素养。教学中要重视知识的系统性,并且要根据学生的知识结构,有针对性地进行教学,鼓励学生一题多解,培养学生的发散性思维,让学生在多种解法中找到适合自己的解法,进行快速解答。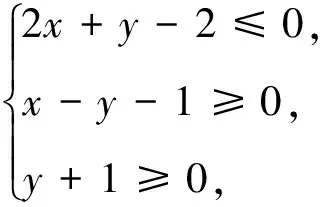
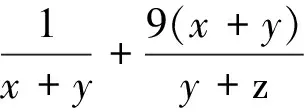
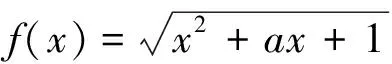
三、总结和建议
(一)关于中学数学中的不等式题目解法研究总结
(二)教学建议
