基于模糊风险矩阵和联系数的区域旱灾风险评估

金菊良，张诗懿，崔 毅，周戎星，周亮广，李 蔓，周玉良

(合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

旱灾是由于降水持续不足，加上人类需求对地表水和地下水供应造成的压力，导致河流、湖泊和土壤含水层的供水相对多年平均大幅度减少而产生的自然灾害，对农业、畜牧业和人饮产生了严重危害[1]。据统计，2012—2016年间，我国因旱灾导致直接经济损失达2 889.7 亿元，占气象灾害总经济损失的15.6%[2]。政府间气候变化委员会工作报告指出，随着全球气温变化加剧，未来旱灾发生的频率将会增加[3]。面对严峻的旱灾形势，世界各国开始寻求应对旱灾的良策。作为干旱灾害科学重要组成部分，旱灾风险评估已成为国内外研究的热点[4]。20 世纪末期以来，众多学者对旱灾风险进行了大量研究，高霞霞等[5]依据历史旱情损失资料，采用旱灾综合风险指数法得出基于GIS 的湖南省旱灾风险指数分区；孙可可等[6]从干旱频率与旱灾损失率之间关系的角度，拟合干旱频率-旱灾损失率的分布曲线研究区域水稻旱灾风险；董涛等[7]建立了基于风险链式传递的风险等级合成矩阵，评估区域旱灾风险等级。目前，旱灾风险评估研究中尚存在若干不足：对旱害风险系统各要素相互作用形成旱害风险机理的传递性的研究不够；评价结果难以反映旱灾系统风险的不确定性；旱灾风险评价等级的计算结果不够精确等。由此可见，如何构建更为合理的旱灾风险评估方法成为目前旱灾风险管理中亟待解决的重要问题。

本文基于旱灾风险系统不确定性特征及旱灾风险链式传递性机理[7]，根据样本指标动态变化信息，构造联系数连接悲观矩阵和乐观矩阵[8-9]来确定风险等级，提出基于模糊风险矩阵和联系数的区域旱灾风险评估方法，并以济南市为实例进行分析评价，可为旱灾风险评估提供新思路。

1 区域旱灾风险评估模型的建立

区域旱灾风险评估模型是基于联系数的模糊风险矩阵而建立的，包括以下6 个步骤：

步骤1：确定风险评估指标体系和评价等级标准。根据旱灾风险评估的概念和目标分析[4-5]，以及旱灾风险评估指标体系的科学性、客观性、系统优化性和实用性原则[10]，综合考虑区域旱灾风险物理成因相关的影响因素[11-12]，可将研究区域旱灾风险评估系统分为敏感性、适应性和危险性3 个子系统，以及属于这些子系统的指标[13]。构建的区域旱灾风险评估指标体系可描述为{Xj|j=1, 2,…,nj}和评价标准等级为{skj|k=1, 2,…,nk}，j=1, 2,…,nj，nj、nk分别为评价指标数目和评价标准等级数目。为进一步探讨风险等级的评估过程，现取评价标准等级nk=5，1～5 等级分别对应低、较低、中、较高、高，其中1 级风险等级最低（最佳等级），5 级风险等级最高（最差等级）。

步骤2：计算单指标联系数。构造第i样本第j指标的样本值xij与旱灾风险评价标准等级skj之间的联系数[14-16]：

式中：s1j ～ s5j分别为1～5 级评价等级标准阈值，s0j为1 级评价标准左端点值，s5j为5 级评价标准右端点值，样本i=1, 2,…,ni（ni为样本数目）；指标j=1, 2,…,nj（nj为指标数目）；评价标准等级k=1, 2,…, 5。根据文献[17]，样本值xij隶属于模糊集“评价标准等级k”的相对隶属度可表示为：

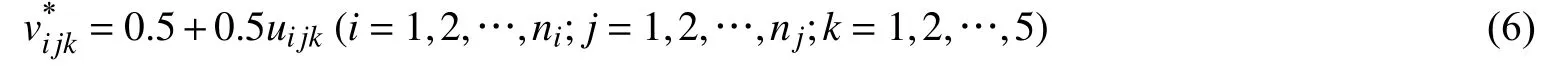
根据文献[18]，对式（6）归一化处理得单指标联系数分量vijk：

根据文献[15-16]，由单指标联系数分量vijk组成指标值联系数uij：

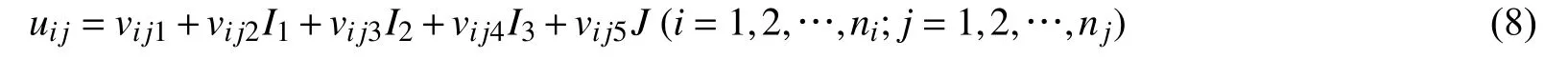
式中：I1、I2、I3为差异度系数；J为对立度系数。由式（8）可得样本值联系数[16]：

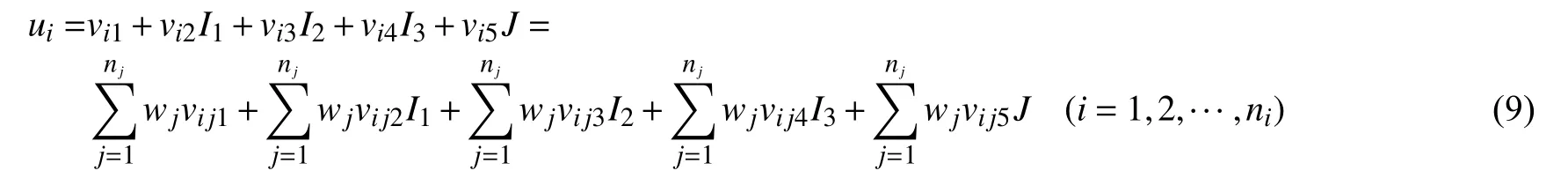
式中：wj为指标权重。

步骤3：确定每个子系统的评价等级。这里将区域旱灾风险评估系统分为敏感性、适应性和危险性等3 个子系统，依据属性识别法[19]得到对应子系统的旱灾风险评价等级值。

式中：λ为置信度，一般取值范围为[0.5, 0.7]，本文取0.6。

步骤4：构造旱灾风险等级的模糊风险矩阵。风险矩阵[7,20]是通过定性和定量分析，将决定风险事件的两方面因素（风险事件发生概率、风险事件影响）先按照特点划分几个等级（如Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ），再构造两维矩阵表格来确定风险评价结果的一种方法。风险矩阵操作简单、工程应用优势明显，是风险评估的常用工具。然而在用风险矩阵进行风险评估、输入变量的值接近相邻区间的临界值时，可能产生两种完全不同的评估结果。这是由于风险矩阵得到的风险等级是一组离散值，尖锐的边界区分风险级别会产生较大差异，缺乏连续变化的过渡性。为得到更为准确的风险等级值，Markowski 等[8]利用模糊集来描述变量，提出了模糊风险矩阵；潘争伟等[9]将联系数与模糊风险矩阵相结合，以水资源系统的自然恢复性和人为适应性两个子系统的联系数值作为模糊风险矩阵的两要素，通过分别定义悲观评判准则和乐观评判准则得到两个极端的风险指数值，采用区间数的形式描述风险（见图1）。传统模糊风险矩阵中的悲观评判准则划分了6 块区域，但风险等级的类别只有5 级，图像中的区域与风险级别无法一一匹配；此外，传统模糊风险矩阵将两个子系统视为同等重要（即只适用于两个子系统等权重的情形），忽略了灾害风险严重性和风险发生概率对子系统风险等级的不同影响程度间的差异性，适用范围具有局限性。本文保留了风险矩阵和传统模糊风险矩阵的优点，重新构造模糊风险矩阵的形式。不失一般性，以旱灾风险系统中的敏感性和适应性[13]评价等级值作为模糊风险矩阵的两要素[9]，构造基于联系数的模糊风险矩阵（见图2）。

图1 传统模糊风险矩阵[9]Fig.1 Traditional fuzzy risk matrix[9]

图2(a)为相对宽松的评判准则，即将敏感性等级与适应性等级中较小的（风险性较低的等级）作为评判标准，并以此构建乐观矩阵A；图2(b)为相对严格的评判准则，敏感性等级和适应性等级两个子系统风险等级合成时，将其中等级较大的（风险性较高的等级）作为评判标准，构建悲观矩阵B[9]。根据模糊风险矩阵的评判准则显然有：

图2 模糊风险矩阵Fig.2 Fuzzy risk matrix

式中：h1为敏感性子系统等级；h2为适应性子系统等级，等级越小风险越低。

步骤5：构造AIA+BJB型联系数[15,21]连接乐观矩阵和悲观矩阵：

式中：A为乐观矩阵；B为悲观矩阵；IA为乐观项系数；JB为悲观项系数。

根据集对分析理论[15]，AIA+BJB型联系数是关于A、B对象的一种结构函数，即表示集合A与集合B之间的“联系”。其中A和B均为非负实数，乐观项系数IA、悲观项系数JB都在[0, 1]区间取值，这里应满足归一化条件IA+JB=1，具体取值根据研究对象偏向悲观还是乐观而定，因此具有不确定性。从集合论的角度看，AIA+BJB型联系数相当于一个正区间数，表示为[A,B]，按照区间数的定义有A>0、B≥A，在整个[A,B]的论域范围内都充满了不确定性，图3 描述了AIA+BJB型联系数在数轴上情形。

图3 AIA+BJB 在数轴上的表示Fig.3 Display of AIA+BJB on number axis

现对乐观项系数IA与悲观项系数JB的不确定性进行分析。由于联系数能深刻描绘不确定性系统，因此可以构建以某一年评价样本为集合Xk和评价标准为集合Yk的集对，然后进行同异反分析，结合式（1）～（9）计算得到样本i的指标值联系数，最后用五元减法集对势[22]计算联系数值：

式中：a表示同一度分量；b1、b2、b3为差异度分量；c为对立度分量。

将五元减法集对势计算的联系数值转化为相对隶属度值[17-18,22-23]：

式中：sf(u)、s分别为表示敏感性或适应性子系统的减法集对势值和相对隶属度值。

由式（14）计算得到敏感性和适应性子系统的相对隶属度值，代入式（15）后得到模糊风险矩阵中的乐观项系数、悲观项系数：

式中：s1与s2分别为敏感性和适应性子系统联系数经减法集对势转化为相对隶属度值中的较大值和较小值。这些系数会随着样本的不同而不断变化，从而实现乐观项系数、悲观项系数的动态变化。将IA与JB代入式（12）得到的联系数值即为模糊风险矩阵合成后的风险等级值，实现了乐观风险矩阵、悲观风险矩阵[9]风险等级极端值变化的连接，改进了现有乐观风险矩阵、悲观风险矩阵[9]无法根据样本变化而动态变化的不足，这显然是对现有乐观风险矩阵、悲观风险矩阵[9]的一种综合、完善。

步骤6：根据旱灾风险链式传递过程，敏感性与适应性合成得到脆弱性子系统。重复以上步骤，继续合成脆弱性子系统和危险性子系统，可最后得到旱灾风险等级值。

2 实例分析

济南市位于山东省的中西部，地处鲁中南低山丘陵与鲁西北冲击平原交接带上，地势南高北低，属于温带半湿润大陆性季风气候，多年平均气温13.8 ℃，全市多年平均降水量581.8 mm，主要集中在5—8月，全市多年平均水资源总量为22.53 亿m3，其中地表水资源量13.63 亿m3，地下水资源量14.64 亿m3[24]。虽然济南有泉城的美称，但市区人均水资源占有量仅225 m3，约为全国人均水资源占有量的十分之一，是典型的资源型缺水城市[25]。

现将上述基于模糊风险矩阵和联系数的区域旱灾风险评估模型应用于济南市1999—2005年旱灾风险评估[13]中。根据济南市的实际情况、参考已有研究[13]，建立由敏感性、适应性和危险性3 个子系统、14 个指标组成的济南市旱灾风险评价指标体系及相应的指标权重[7,13]，如表1 所示。

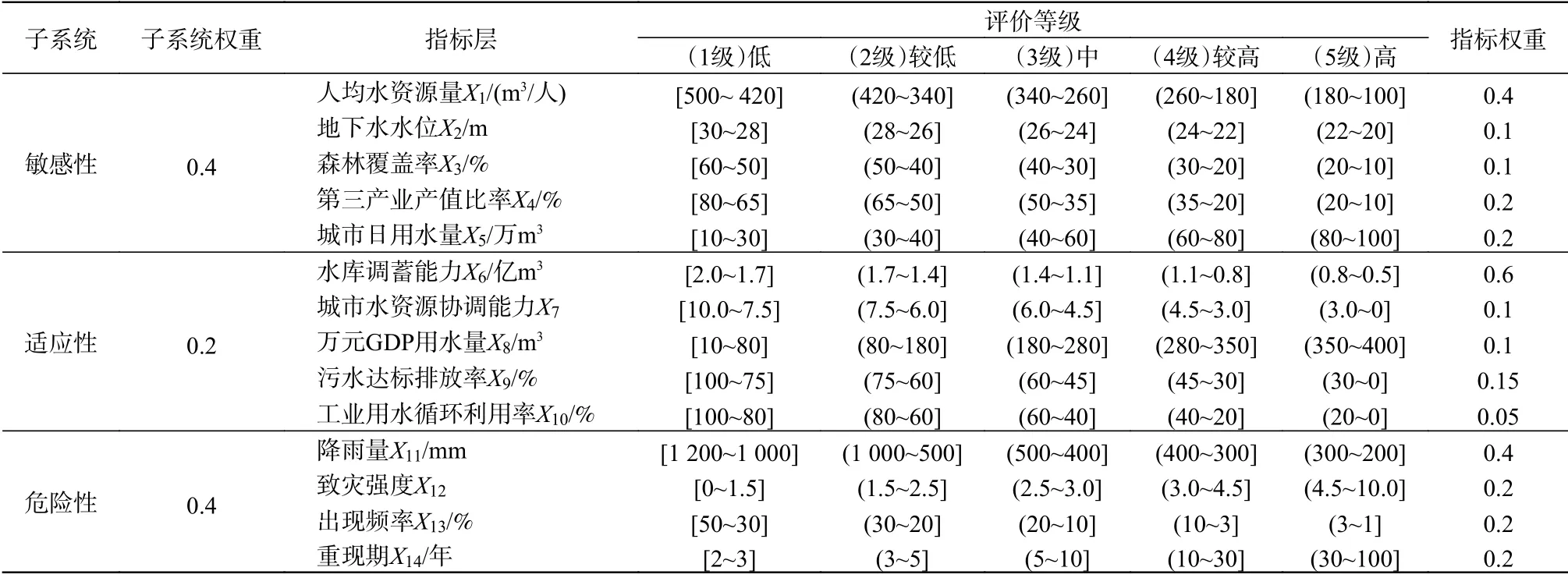
表1 济南市旱灾风险评价指标、权重与等级标准[13]Tab.1 Drought risk assessment index, weight and grade standard in Jinan City[13]

为提高基于模糊风险矩阵和联系数的区域旱灾风险评估方法在风险评估中的合理性和有效性，将风险等级划分为“低、较低、中、较高、高”5 个等级。把文献[13]中的指标样本数据值代入式（1）～（9）计算得济南市旱灾风险评价各年样本联系数见表2。

表2 济南市旱灾风险子系统各年评价样本联系数[7]及评价等级Tab.2 Connection number[7] and evaluation grade of evaluation samples of drought risk subsystem in Jinan City in each year

根据表2 中的属性识别法[19]计算出敏感性子系统、适应性子系统的评价等级，比较两个子系统的评价等级的大小，结合上述约定的评判准则，将级别较小的等级（风险低）作为乐观等级，级别较大的等级（风险高）为悲观等级。由式（12）～（15）模糊风险矩阵法确定脆弱性子系统的风险评估等级值与承灾体脆弱性指数法[13]、风险矩阵法[7]对比情况如表3 和图4 所示。

表3 3 种评估方法的脆弱性风险评估结果Tab.3 Vulnerability risk evaluation results of three evaluation methods

图4 3 种评估方法的脆弱性评估结果对比Fig.4 Comparison of vulnerability evaluation results of three evaluation methods

由表3 和图4 可知：（1）运用本文评估方法得1999年、2000年的济南市脆弱性等级均为4 级；2001年脆弱性等级超2 级比较多，比较接近3 级；2002—2005年的济南市脆弱性等级都是接近2 级，变化幅度小。（2）运用风险矩阵法得出1999—2000年脆弱性等级为4 级，2001—2002年脆弱性等级为3 级，2003—2005年脆弱性等级为2 级，等级刻画偏粗糙。（3）运用承灾体脆弱性指数法得出济南市脆弱性指数值由1999年的1.903 下降到2005年的1.375，等级评价结果呈改善趋势，但是2001年后济南市旱灾风险系统的适应性能力得到显著提升，而脆弱性指数却没有明显下降。（4）从整体趋势看，本文评估方法与风险矩阵法、承灾体脆弱性指数法得出的结果总体上一致，即1999—2005年脆弱性等级呈逐年下降趋势，但也存在一定的差异。利用本文评估方法与承灾体脆弱性指数法得出的脆弱性等级可分为两个阶段：1999—2002年为第一阶段，脆弱性等级值下降趋势较快，特别是2000—2002年下降幅度最大。这一时期水库调蓄能力得到大幅度提升，由2000年的0.77 亿m3上升到2002年的1.97 亿m3，故脆弱性等级值降低明显；2002—2005年为第二阶段，脆弱性等级值变化不大，较为稳定。而风险矩阵法反映的各年脆弱性等级呈阶梯式下降，没有变化缓慢过渡的第二阶段。（5）从指标数值看，2002—2005年各指标数据无较大差异，如权重较大的指标水库调蓄能力各年数据均为1.97 亿m3，因此2002—2005年脆弱性等级值应比较接近更为合理，而风险矩阵法计算出的等级出现明显下降，与实际情况不符。

将计算的各评价样本与脆弱性等级间的联系数与基于模糊风险矩阵和联系数的脆弱性等级进行整理，结果如表4 所示。

表4 济南市脆弱性联系数分量[7]、相对隶属度及脆弱性等级Tab.4 Vulnerability connection number component[7], relative membership and vulnerability grade in Jinan City

同理，以脆弱性等级与危险性等级作为模糊风险矩阵的两个要素，重复本文小节1 的步骤4～5，即可得到1999—2005年济南市的旱灾风险综合等级，并与干旱风险评价指数法[13]、短板法[7]（选取子系统中最差的评价结果作为综合评价结果）、风险矩阵法[7]的计算结果进行对比，如表5 和图5 所示。

表5 不同评价方法旱灾风险综合评价等级结果比较Tab.5 Comparision of drought risk comprehensive evaluation grades of different evalution methods

图5 不同评价方法旱灾风险综合评价等级的计算结果Fig.5 Results of the comprehensive evaluation of drought risk by different evaluation methods

由表5 和图5 可知：（1）根据本文评估方法，1999—2000年的济南市风险等级从超3 级下降到接近2 级；2001—2002年的济南市适应性风险有所改善，但受降水量减少的影响，相应地下水水位下降，导致风险等级突增至2.544 级；2003—2005年，济南市降雨量丰沛，旱情得到缓解且济南市政府充分利用全市的水源蓄水工程，增加水库调度，旱灾风险等级有了明显降低。（2）从风险等级的变化来看，本文的评价结果总体上由超3 级向接近1 级的趋势发展，随时间的推移济南市旱灾风险等级值总体呈下降、改善趋势，这与干旱风险评价指数法、风险矩阵法的评价结果的趋势较为一致；用短板法呈现的各年风险等级变化为一条水平线，没有体现各年的细节变化。（3）短板法直接采用子系统中计算结果最不利的评价等级作为旱灾风险评价等级，这种方法得到的风险等级较为保守，容易受到某单一要素的评价结果的影响，不能客观反映出旱灾风险的实际状况。（4）干旱风险评价指数法可呈现旱灾风险的下降趋势，但未考虑旱灾风险子系统相互作用机理，风险矩阵法虽然考虑了灾害风险系统各要素相互作用灾害形成机理的传递性，但在评价等级精度方面低于基于模糊风险矩阵和联系数的风险评估评价结果。（5）从风险评价等级值来看，本文评估方法计算的风险等级值总体比干旱风险评价指数法明显降低，相较于指数法浮动更小，这是因为本文模型利用了风险评价结果随评价样本指标值的动态变化信息，提高了评价模型的适应性和评价结果的可靠性。（6）本文在考虑子系统间相互作用的基础上，根据指标样本动态变化特征运用AIA+BJB型联系数连接悲观矩阵和乐观矩阵合成风险等级，反映了各年旱灾风险的动态变化。相较于风险矩阵法，本文方法在判别各子系统旱灾风险评价等级时更加细致、富有弹性，符合实际情况。

研究实例结果表明，本文模型运用了AIA+BJB型联系数连接悲观矩阵和乐观矩阵合成脆弱性风险等级，提高了风险矩阵定性确定风险等级的精准程度，增强了旱灾风险等级评价的精准性；将合成得到的脆弱性子系统等级值与危险性等级值作为模糊风险矩阵的两个要素，综合得到区域旱灾风险等级评价值，验证了旱灾风险从危险性经脆弱性到风险等级的风险传递过程的合理性。

3 结 语

以济南市1999—2005年旱情数据为评价样本，依据联系数和模糊风险矩阵原理，提出了基于模糊风险矩阵和联系数的区域旱灾风险评估方法，评估济南市综合旱灾风险等级。通过对实例的分析得出如下结论：

（1）本文方法依据旱灾风险系统不确定性特征及旱灾风险链式传递性机理，重新构造了基于联系数的模糊风险矩阵，以敏感性和适应性等级作为模糊风险矩阵的两要素合成为脆弱性子系统等级，将合成得到的脆弱性子系统等级与危险性子系统等级进一步合成，综合得到最终的风险等级值，实现了旱灾风险的链式传递，反映了旱灾风险子系统之间的相互作用和内在联系。采用基于模糊风险矩阵和联系数的区域旱灾风险评估方法更符合实际旱灾风险传递的物理过程，克服了干旱风险评价指数法忽略旱灾风险子系统相互作用机理的缺点，增强了风险等级评估过程的合理性。

（2）根据样本指标动态变化信息，采用联系数连接悲观矩阵和乐观矩阵来确定风险等级，克服了传统模糊风险矩阵只能解决两个同等重要子系统合成的局限性。本文方法避免了短板法进行多要素合成时忽略其他要素的重要性，弥补了评价结果与实际风险状况存在差异的不足，克服了风险矩阵法评价结果的跳跃性和粗糙性，提高了风险矩阵定性确定风险等级的精准性。

（3）基于新方法得到的济南市综合风险等级值随时间增长呈降低趋势，区域抗旱能力得到明显提升，风险状况也得到改善。评价等级从1999年的超3 级水平改善到2005年的接近1 级的水平，在2001—2002年出现小幅波动，风险整体趋于降低。