恒久的数学定理

王治钧

西班牙数学家爱德华多

数学的意义是什么？

如果有人问，数学的意义是什么，你会怎么回答呢？有些数学家对这个问题的回答是，数学本身就是意义。他们认为，一套能自圆其说的逻辑系统本身就是意义，为什么一定要给它找一个“用处”？

有些数学家属于谆谆善诱型，就像你的数学老师，他们会更温和地告诉你：“你可能意识不到，数学蕴藏于万物之中。”科学家、工程师利用数学理论获得了现实中的进步。建筑、人工智能、航天探测等领域更是离不开数学，不懂数学你造的桥可能会垮塌，飞船可能会出现故障，亦或给复杂山地的智能无人果园带来损失。

还有一部分数学家对这个问题的回答是：数学让我们更好地认识世界。

确实，数學不需要为某个“意义”而存在，它本身就是一套精美而又逻辑自圆其说的系统，是人类历史上集众人思想合力的伟大成就之一。数学的精美构造几乎渗透于万事万物当中。

提起数学，你会想到什么？是随处可见的阿拉伯数字，还是课本上复杂深奥的数学公式？数学存在的意义是什么？数学家们是如何发掘一个数学定理的？让我们听听西班牙数学家爱德华多（EduardoSáenz de Cabezón）是怎么说的。

走出混沌

如果我们更进一步深入思考科学，去看看它背后有什么样的奥妙，就会发现，科学和艺术一样，它的运转同样离不开一定程度的直觉和创造力，而数学驯服了天马行空的创造力和千丝万缕的直觉。

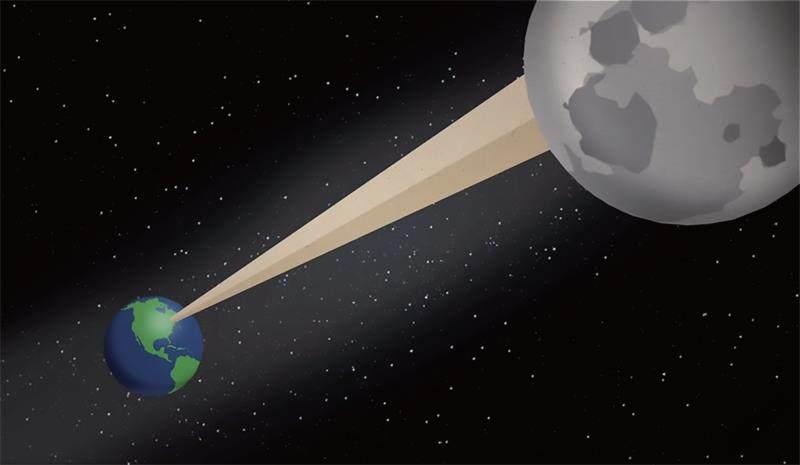
拿一张A4纸对折50次后，纸的厚度几乎相当于地球到太阳的距离（约1500万千米）。直觉会告诉你“这不可能”！但是如果你通过数学计算来验证一下就会发现，这确实是真的。

这就是数学的意义——帮你走出混沌，更好地认识世界！

其实，所有科学都是如此，既能够帮助人类认知世界之美，也能帮助人们避免某些糟糕的结果，这就是意义。有些科学对人类发挥直接作用，比如肿瘤学。有些只能远观，然而它们却是支撑其他学科发展的基石，数学就是这样一门基础科学。科学的严谨来自蕴含其中的数学构造本身的严谨，而数学的严谨来自其研究成果无限追求逻辑的自圆其说。

从地球到月球的纸梯子

勾股定理

威尔-弗兰多面体

寻找定理

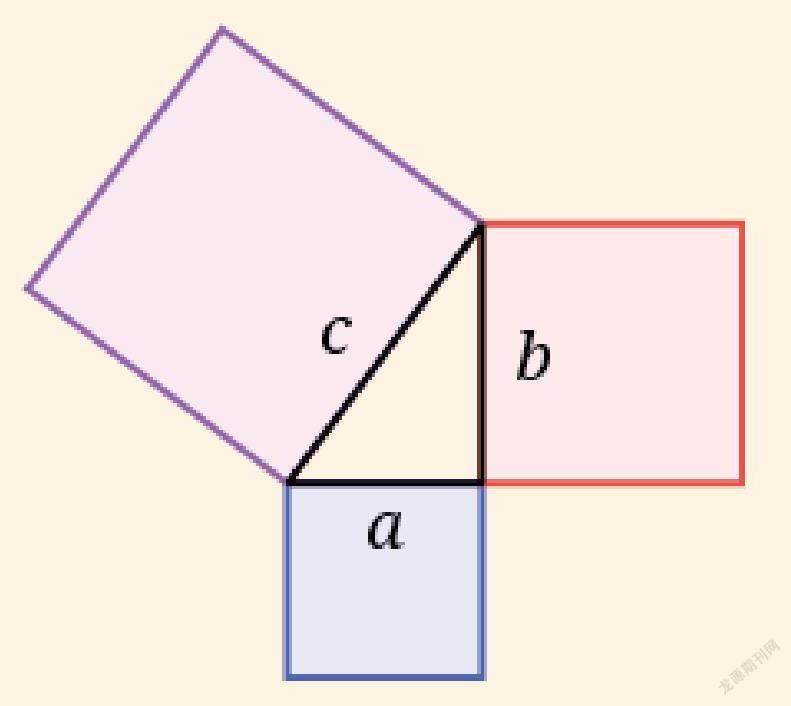
不知道你有没有听过这句话：钻石永恒。钻石作为最坚硬的宝石，在人类科学的时间尺度上，一颗钻石几乎可以持续到永远。你又是如何看待“永恒”这个词的呢？在数学家眼中，数学定理才是流传后世，禁得起时间考验的智慧瑰宝。商高（又名殷高，中国古代周朝数学家）和毕达哥拉斯（古希腊数学家）已经尘归尘、土归土，但是勾股定理提起数学，你却超越了这些人存在的时间，并将继续向前。只要有一个直角和一个合适的斜边相结合，勾股定理就呱呱坠地，屡试不爽让人称奇。

数学家们将自己的一生奉献给了对定理的发掘。浩瀚无垠的数学理论中，哪些可能是有待证明的定理，哪些是无法验证的猜想，甚至哪些是错误的理论呢？这个过程就像是在沙滩上寻找最美的贝壳，尽管有时你会捡到石头或瓶盖。一代又一代数学家在数学的沙滩上发掘钻石般长久的定理，这其中的过程不止一支笔、一张纸的论证。

由正六边形组成的蜂巢

比如，蜂巢定理的发掘前后跨越了1700年之久。如果有一个无限大的二维平面，我们要用形状一致的元素不留任何缝隙地覆盖它，哪个形状才是最佳选择？我们可以用方形，也可以用三角形，但圆形就需要被淘汰，因为圆形会留下缝隙。数学家们追求的是不留缝隙，周长最短，覆盖面积最大的最优图形。公元4 世纪，古希腊数学家佩波斯提出，正六边形——例如苯与石墨的分子结构、龟壳、蜂巢等，就是覆盖二维平面的最佳结构。但佩波斯并没有去验证这个想法，所以这个理论被人们称为蜂巢猜想。直到1999年，数学家黑尔斯证明了正六边形就是最优选择，而此时已是这个猜想提出的1700年以后了。

于是“正六边形是最优解”这个猜想从此作为“蜂窝定理”流传，不但有力推动了建筑、计算机学科的发展，还影响到超市货物的摆放、鸡蛋盒的制作，在提高人们生活质量的同时，更在视觉上增添了秩序之美。

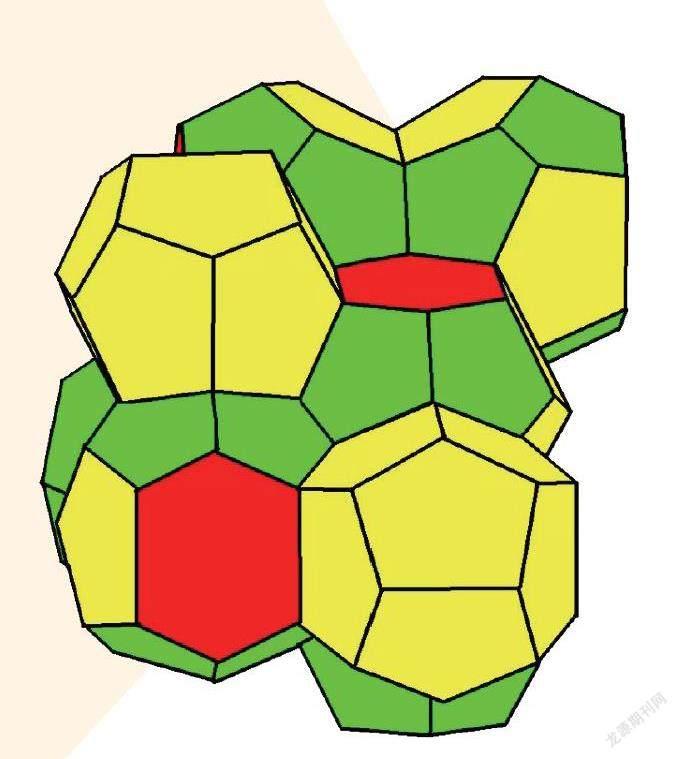
如果在三维空间中提出这个问题呢？如果我想用一个元素填充三维空间不留缝隙，谁是最优图形？立方体是一个选择，而曲面体就不可以了，会留下缝隙。开尔文爵士，即热力学第二定律的提出者认为，最好的结构是截角八面体，但他并没有证明这个想法。所以人们把他提出的“截角八面体是填充三维空间的最佳结构”这一理论称为开尔文猜想。

基于“威尔-弗兰多面体”结构建造的“水立方”

有人支持开尔文，也有数学家持反对意见。在反复研究且尝试论证这一理论的100年后，终于有人找到了更好的选择——数学家威尔和弗兰发现了一个结构，并将它命名为威尔-弗兰多面体。它看起来像是个奇怪的物件，但其实没有那么特别，这种结构在自然界中随处可见，非常有趣。鉴于它的几何特性，北京奥运会的“水立方”就采用这种结构建造。接下来，如果没有人发现更好的结构，威尔- 弗兰多面体就是迄今为止人类发掘出的最佳图形。如果这个多面体在100年甚至1700 年后，被某位数学家证明就是最佳选择，那么它就会像勾股定理一样流传后世，成为“威尔-弗兰多面体定理”。

生活中的数学

数学对人类的影响不止高科技，也与生活有关。超市货物摆放呈现的几何形状，小小鸡蛋盒表现出的可视化空间图形设计，让数学的“秩序”和“协调”之美渗透于生活之中。那么还有哪些人类的日常活动，离不开数学知识呢？我们来看一个例子。

如果你面前有100个苹果，而你只能按顺序一个一个去选择，那么第几个苹果，有可能会是最大的一个呢？如果你选了第一个苹果，可能会错过后面大量更大的苹果。但如果你一直惦记着“后面还有更大的”，而放弃了前99个苹果，第100个有可能是最小的。只要苹果多于两个，直接选第一个或者最后一个，都是有风险的。

但我们如果从数学的角度看问题，运用概率知识，就能够提出一个不靠直觉或运气，而是通过精确计算得出的解决方案。不妨从这堆苹果里选出一部分看一看，这样你就能了解这些苹果大概有多大。然后，再从剩下的苹果里，选出一个比你看到的最大的苹果要大的苹果。

那么先看一看的这部分苹果又该选多少个呢？我们计算一下就会发觉这个数值是37%。也就是100个苹果中的前37 个只看不选，从后63个当中选，是最有可能选出最大苹果的方案。它虽然不能帮你作出绝对正确的选择，但是至少可以让你避免因为怕选不到大的而一拖再拖，最后一无所获，或者太过心急直接选了第一个，错过后面更大的选择这种局面。这就是前文所说的——数学，既能够帮助人们认识世界之美，也能够帮助人们避免一些糟糕的结果。

数学是发明还是发现

既然数学如此无处不在，那么第一个提出“数学”的人是谁呢？数学到底是人类智慧发明创造的产物，还是原本就蕴含于自然界之中，像所有山川河流一样是自然界的一部分？如果在森林中有很多樹，但是没有人去数它，那么数字还存在吗？这些问题，让人类对“数学”更加着迷，对它的探寻更加深入，于是有些数学家就像我们开篇所提到的那样，视数学为自然界的精髓，提出“数学本身就是意义”。正如笛卡尔所说的：我思，故我在。

数学蕴藏于万物，支撑科学的严谨和秩序美。数学不仅是肉眼可见的数字、桥梁，更是久经时间考验的定理。当人类被自我认知所困，数学是人类走出混沌的地图。它的意义是它本身，更是永恒的智慧结晶。

（责任编辑 / 李晓霏 美术编辑 / 周游）