基于STL-EEMD-GA-SVR 的采煤工作面瓦斯涌出量预测方法及应用

林海飞，刘时豪，周 捷，徐培耘，双海清

(1.西安科技大学 安全科学与工程学院，陕西 西安 710054；2.西安科技大学 煤炭行业西部矿井瓦斯智能抽采工程研究中心，陕西 西安 710054)

瓦斯是影响矿井安全生产的主要因素之一，随着煤炭开采深度及强度增大，矿井瓦斯涌出量也逐渐增加[1-3]。瓦斯涌出量的准确预测可为制定瓦斯防治措施提供重要依据[4-5]。针对瓦斯涌出量预测，传统的矿山统计法、分源预测法、瓦斯地质统计法和类比法等尚未考虑瓦斯涌出是一个动态非线性系统[6-8]。

为解决该问题，基于机器学习算法、数据挖掘等技术的瓦斯涌出量动态预测方法得到了快速发展。此类预测方法主要分为考虑多参数指标和时间序列两类。根据影响瓦斯涌出量诸多参数建立起的多参数指标预测方法[9-15]，大多数煤矿只能提供瓦斯涌出量历史数据，对于影响瓦斯涌出量的煤层厚度、邻近层瓦斯含量等相关数据难以详尽[16]，加之对影响参数取舍不同，使得建立的预测模型与实际情况仍有一定差距。因此，诸多学者开展了瓦斯涌出量时间序列的预测研究分析。陶云奇等[17]将改进的灰色模型与马尔柯夫模型结合建立了中岭煤矿瓦斯涌出量预测模型；高莉等[18]利用混沌时间序列特性构建了小波-径向基神经网络预测模型；单亚锋[19]、程健[20]等通过对时间序列进行相空间重构构建了瓦斯涌出的混沌预测模型；在以上研究基础上引入信号分解中的经验模态分解方法，预先对瓦斯涌出量时序数据进行分解处理，而后运用支持向量机、粒子群-支持向量机、果蝇-极限学习机等模型对其预测，进一步提升了瓦斯涌出量预测精度[8,21-24]。

但基于经验模态分解构建的预测模型，分解过程中若瓦斯涌出量时序数据极值点分布不均匀会出现模态混叠、端点效应等问题，进而影响预测精度；同时，瓦斯涌出量时序数据作为众多影响因素的综合表征，需进一步从时序数据本身来挖掘其潜在规律。因此，笔者以陕西黄陵某矿采煤工作面347 个日监测绝对瓦斯涌出量数据为例，应用基于局部加权回归的周期趋势分解(Seasonal-Trend decomposition procedure based on Loess，STL)和集成经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)进行数据分解，通过遗传算法(Genetic Algorithms，GA)参数寻优后的支持向量回归机(Support Vector Regression,SVR)构建了可以挖掘数据本身潜在规律的STL-EEMD-GA-SVR预测模型(简称SEGS)，并与EEMD-GA-SVR、GA-SVR和高斯过程回归(Gaussian Process Regression,GPR)模型预测效果进行对比分析，以期为瓦斯涌出量的精准预测提供有效方法。

1 瓦斯涌出量预测模型建立

1.1 基于局部加权回归的周期趋势分解(STL)

时序数据通常可被分解为趋势项、周期项和不规则波动项3 部分[25]。工作面日产量、日推进度、煤层和围岩瓦斯含量、地面大气压、地质构造、开采深度及风量等都会对瓦斯涌出量产生影响[26]，其中开采深度、煤层和围岩瓦斯含量等对工作面瓦斯涌出量产生趋势性影响；日产量、日推进度及风量等对工作面瓦斯涌出量产生周期性影响；地质构造变化、大气压力变化、周期来压等对工作面瓦斯涌出量产生突变影响，这些因素影响都可表征于瓦斯涌出量时序数据。直接使用原始数据，会使数据利用不充分，因此，采用STL分解算法对瓦斯涌出量时序数据进行分解处理[27-28]。

STL 包括加法和乘法2 种模型[29]，均可将时序数据分解为趋势项Tt、周期项St和不规则波动项It：

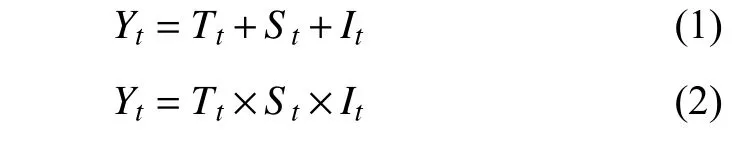
加法模型适用于相对稳定数据分解，乘法模型适用于趋势项随时间呈现波动变化的数据分解。由于所分析瓦斯涌出量数据整体时序图呈相对稳定状态，因此，选用加法STL 时间序列对数据进行分解。

STL 关键参数设定：控制趋势效应变化速度的t.window 设为13，控制周期效应变化速度的s.window设为“period”，Loess 过程使用鲁棒拟合即robust=T。

1.2 集成经验模态分解(EEMD)

瓦斯涌出量时序数据经STL 分解后，会得到波动较大、尖峰较多的不规则波动项，此类数据不利于模型训练学习。EEMD 方法通过在待分解信号中加入白噪声，可有效抑制经验模态分解混叠现象[30-31]。因此，采用EEMD 方法将瓦斯涌出量分解为具有不同特征尺度、尖峰和波动更缓的时序分量数据。EEMD 分解原理如下：

(1) 将符合正态分布的白噪声信号加到原始信号中：

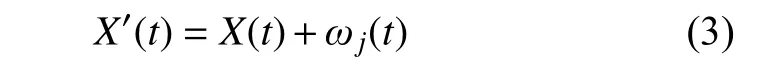
式中：X(t)为原始信号；ωj(t)为白噪声信号；X'(t)为生成的新信号序列；j=1,2,···,M，M为测试次数。

(2) 新信号序列进行EMD 分解，得到IMFs(Intrinsic Mode Functions，IMFs)分量：

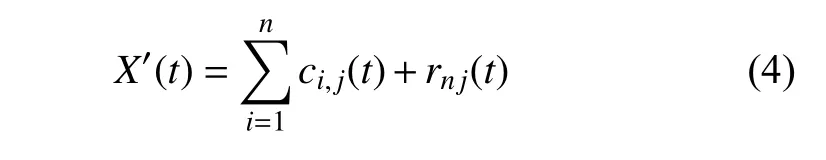
式中：n为经EMD 分解得到的IMFs 分量个数；ci,j(t)为在第j次实验分解中的第i个IMFs 分量；rnj(t)为分解得到的残差余量。

(3) 重复上述(1)、(2)步，每次加入不同正态分布的白噪声。

(4) 对各IMFs 分量求均值得到最终IMFs 分量：

EEMD 关键参数设定[32]：白噪声标准差设为0.2，白噪声次数设为100。

1.3 GA-SVR 模型

SVM 在处理小样本、非线性以及高维识别问题上优于其他机器学习算法[33]。SVR 则是在SVM 基础上通过引入不敏感损失函数实现了回归功能，其具体实现步骤如下：

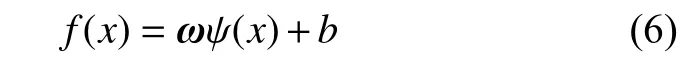
(1) 假设高维空间的回归函数为：式中：ω为权值向量；ψ(x)为非线性映射函数；b为偏置值。

(2) 引入线性不敏感损失函数ε，松弛变量ξi，并求解以下最优化问题：

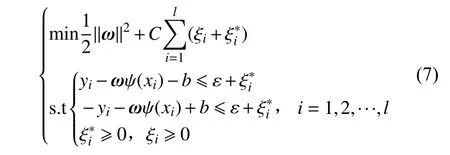
式中：C为惩罚因子；l为样本集个数。

(3) 对式(7)引入拉格朗日函数，求解得到最终回归函数：

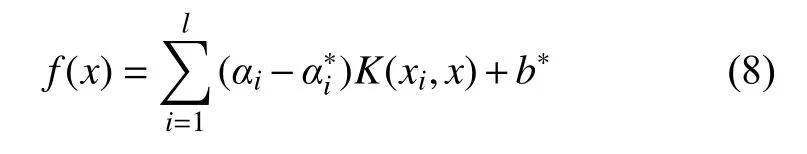
SVR 独立预测时，其惩罚因子C和核函数gamma为经验设定，难以保证模型参数最优。GA 作为一种具有良好并行性、鲁棒性和全局寻优能力的自适应全局随机搜索优化算法[34]，可有效解决此问题。为此引入GA 对SVR 关键参数全局寻优，以期建立最优GASVR 模型。

GA 优化SVR 关键参数设定：最大遗传迭代次数100，种群大小40，交叉概率0.3，变异概率0.01，代沟0.95；惩罚因子C寻优范围为[0.01,10]，gamma 参数寻优范围为[0.01,1 000]，交叉验证参数v为3。

1.4 瓦斯涌出量预测模型构建流程

根据以上分析，构建瓦斯涌出量SEGS 预测模型流程如图1 所示，具体步骤如下。

图1 瓦斯涌出量预测模型总框架Fig.1 Overall framework of gas emission prediction mode

(1) 数据处理。对缺失、异常样本集数据进行线性插补。

(2) 时序数据分解。STL 分解算法将线性插补后数据分解成趋势项、周期项和不规则波动项；EEMD分解算法在此基础上将不规则波动项再次分解，获得各IMFs 分量及RES 残差余量。

(3) 模型预测。将STL 和EEMD 分解数据分为训练集、预测集并作归一化处理，利用训练集数据进行模型训练获得最佳GA-SVR 模型，运用预测集数据使用GA-SVR 模型进行预测，并对预测结果进行反归一化处理，获得各分解分量预测结果。

(4) 分量叠加。将各分量预测结果进行叠加求和，获得最终瓦斯涌出量预测结果。

(5) 模型效果评价。选用平均绝对误差(EMA)、平均绝对百分比误差(EMAP)、均方根误差(ERMS)和判定系数(R2)对预测模型效果评估。其公式如下：

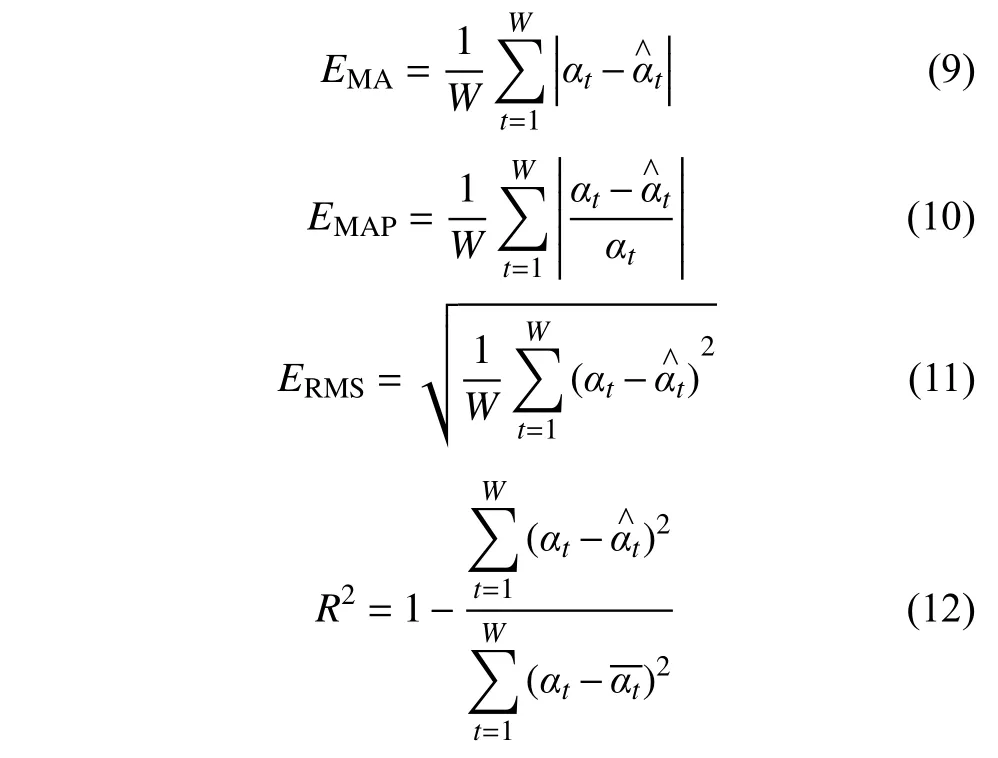
式中：αt为瓦斯涌出量原始数据，m3/min；为瓦斯涌出量预测数据，m3/min；t=1,2,···,W，d。

2 瓦斯涌出量数据处理

2.1 数据获取及检测

以陕西黄陵某矿采煤工作面为研究对象。该工作面主采2 号煤层，煤厚平均3.0 m，煤层倾角平均2°，瓦斯含量0.61～7.70 m3/t，采用本煤层钻孔、高位钻孔和上隅角埋管等方法抽采工作面瓦斯。收集该工作面2020-05-16—2021-04-27 瓦斯风排量和抽采量数据，得到绝对瓦斯涌出量数据，见表1。

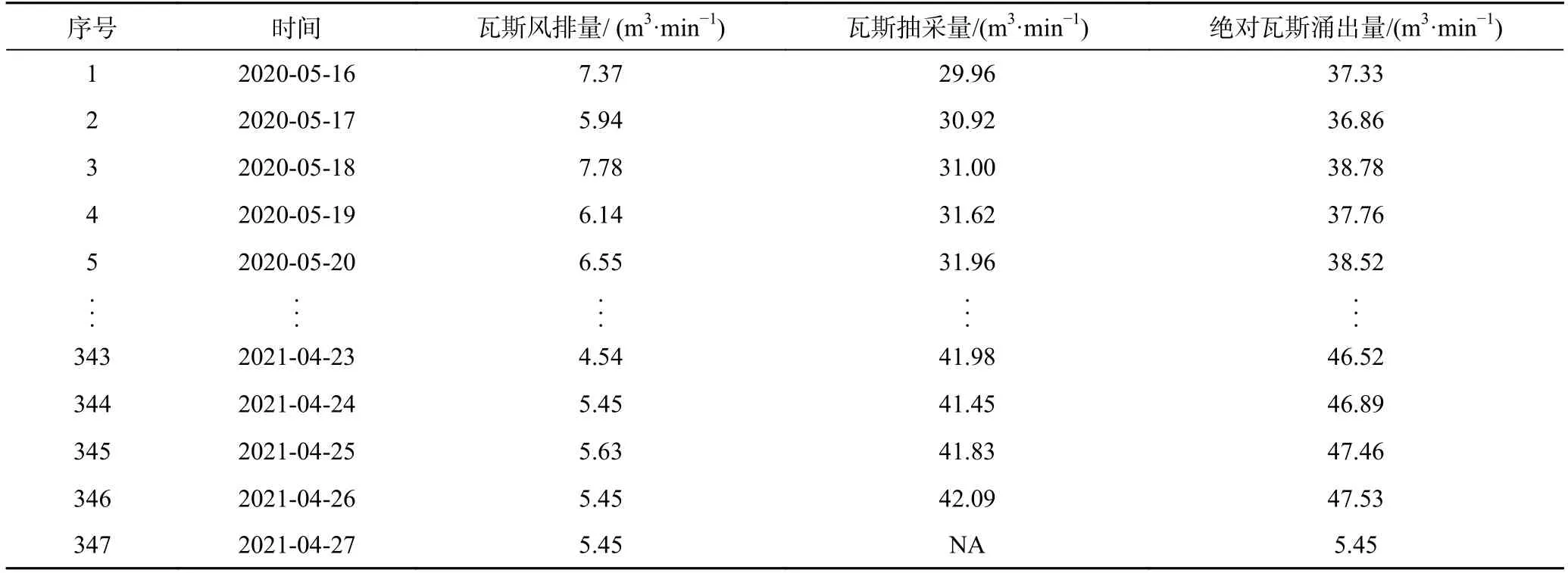
表1 瓦斯涌出量数据Table 1 Gas emission data

为保证模型预测精度，构建模型之前需对收集数据进行异常值及缺失值检测。将±1.5IQR(IQR 表示四分位距)之外数据点作为异常值，以此为标准绘制如图2 所示箱线图。由图中可知，所搜集数据均在正常区间范围。针对缺失值通过语句shuju[!complete.cases(shuju),]获得，见表2 共6 组。

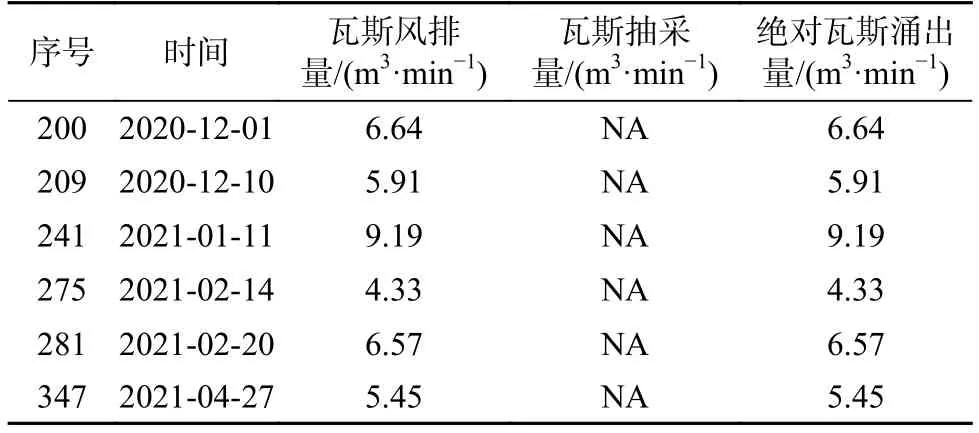
表2 瓦斯涌出量缺失数据Table 2 Missing data of gas emission

图2 异常值判别箱线图Fig.2 Outlier discriminant boxplot

2.2 数据插补

时间序列模型一般需保证时序数据的完整性，若直接剔除缺失值，容易导致数据周期错位。为保证数据完整性，需作数据插补处理。目前常用插补方法有均值插补、线性插补、多重插补和EM 插补[35]等。为优选出所收集数据的最佳填补方法，本文将原始数据中不包含缺失值的涌出量数据(2020-05-16—2020-08-23)作为试验完整样本，在随机缺失情景[36]利用均值插补、线性插补和多重插补进行插补实验，并将插补结果与实际值进行均方误差[37]比较，以此评估各方法插补精度。各插补方法均方误差见表3。

由表3 可知，线性插补的插补精度最高。为此，本文选用线性插补方法插补缺失值，插补结果见表4。

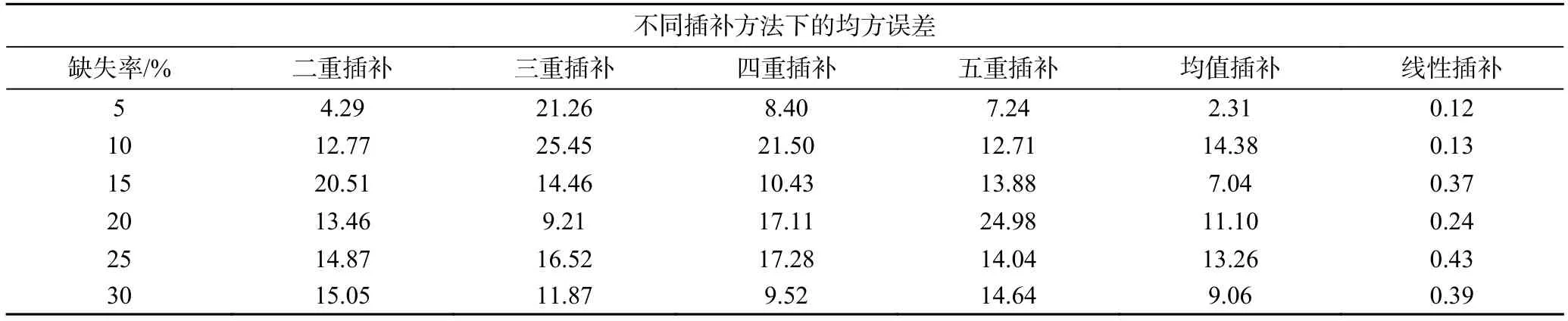
表3 随机缺失插补误差对比Table 3 Comparison of interpolation error for random missing values

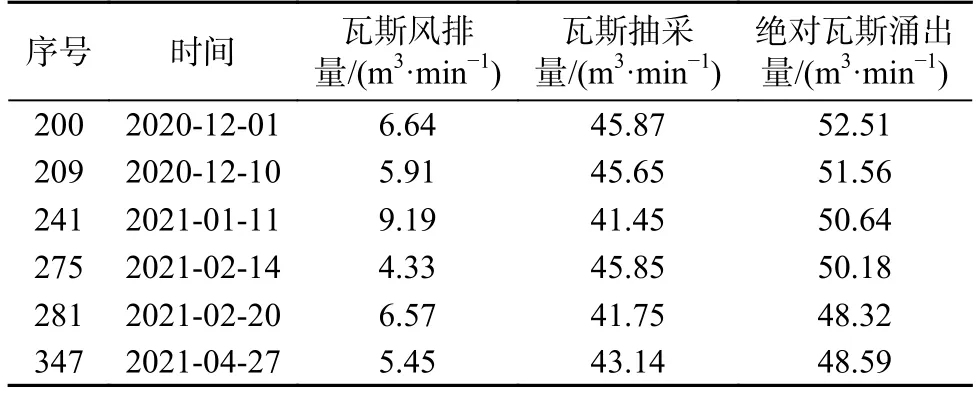
表4 线性插补填补数据Table 4 Linear interpolation fill data values

3 瓦斯涌出量预测及效果检验

3.1 瓦斯涌出量数据的时序分解

经线性插补后的数据自2020-05-16—2021-04-27 共计347 组。针对瓦斯涌出量时序数据作STL 分解，经分解得到趋势项、周期项和不规则波动项，如图3 所示。

图3 STL 分解后采煤工作面瓦斯涌出量Fig.3 Gas emission data of mining workface after STL decomposition

由图3 可知，趋势项和周期项可以提取出大部分有效信息：趋势项反映了瓦斯涌出量在搜集时间段内的整体变化特征，通过此分解序列可知该工作面瓦斯涌出量初期较小，之后瓦斯涌出量在50～60 m3/min 波动，具有一定的线性特征；周期项符合待分析时间序列平稳性的要求，规律性强，有利于GA-SVR 模型的训练学习。不规则波动项主要为一些未被趋势或周期效应解释的变化，剩余信息较少，从分解图中可知其具有较强的波动性和随机性，波动和尖峰较多，不利于构建时间序列预测模型。

为降低不规则波动项的波动和尖峰影响采用EEMD分解算法对其进行平稳化处理，结果如图4 所示。

图4 不规则波动项EEMD 分解Fig.4 EEMD decomposition of irregular fluctuation term

由图4 可知，不规则波动项经EEMD 分解得到7 个IMFs 分量和1 个RES 残差余量。分解后的各分量数据相较于最初数据，其振动周期逐渐增加、波动趋势逐渐减缓，平稳性明显优化。

为评估EEMD 分解后的数据是否会造成不规则波动项中突变信息的丢失。将不规则波动项与EEMD分解分量叠加值作对比(图5、表5)。

由图5、表5 可知，经EEMD 分解分量叠加后的数据曲线与不规则波动项曲线呈重合态；数据分解损失量较小，平均分解损失量为0.000 4 m3/min。EEMD分解分量在保留原始数据信息的情况下，降低了原始数据复杂度，提升了平稳性，更有助于预测模型学习其特征进而提高预测精度。

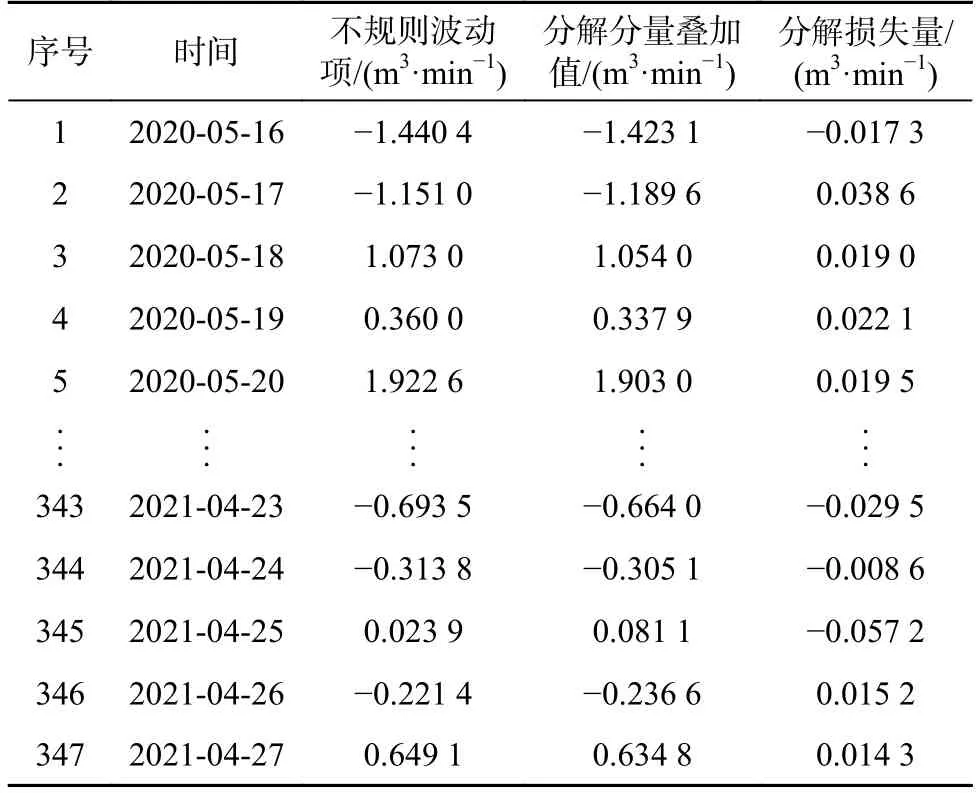
表5 分解损失量Table 5 Decomposition loss

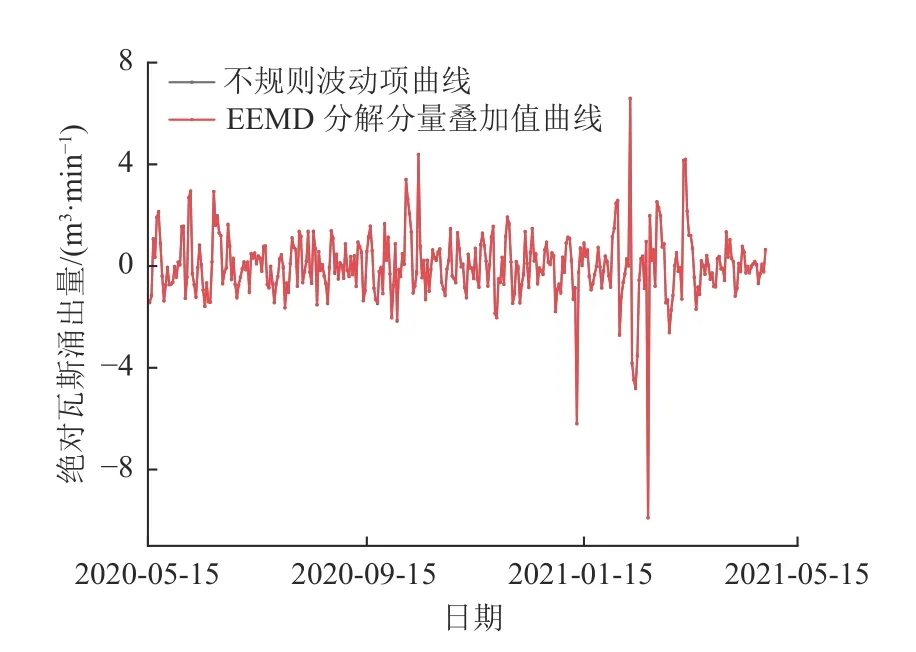
图5 不规则波动项与EEMD 分解分量叠加值对比Fig.5 Comparison of irregular fluctuation term with superposed value of decomposition components by EEMD

3.2 瓦斯涌出量预测

为验证分解序列预测效果，将分解数据按一定比例分为训练集与预测集，共划分3 种情景(情景一：训练集100 组，预测集247 组；情景二：训练集200 组，预测集147 组；情景三：训练集277 组，预测集70 组)。

运用训练集数据实现GA 对各分量SVR 模型超参数寻优，其寻优值见表6。以此确定各分量最佳模型参数，完成GA-SVR 预测模型的构建。

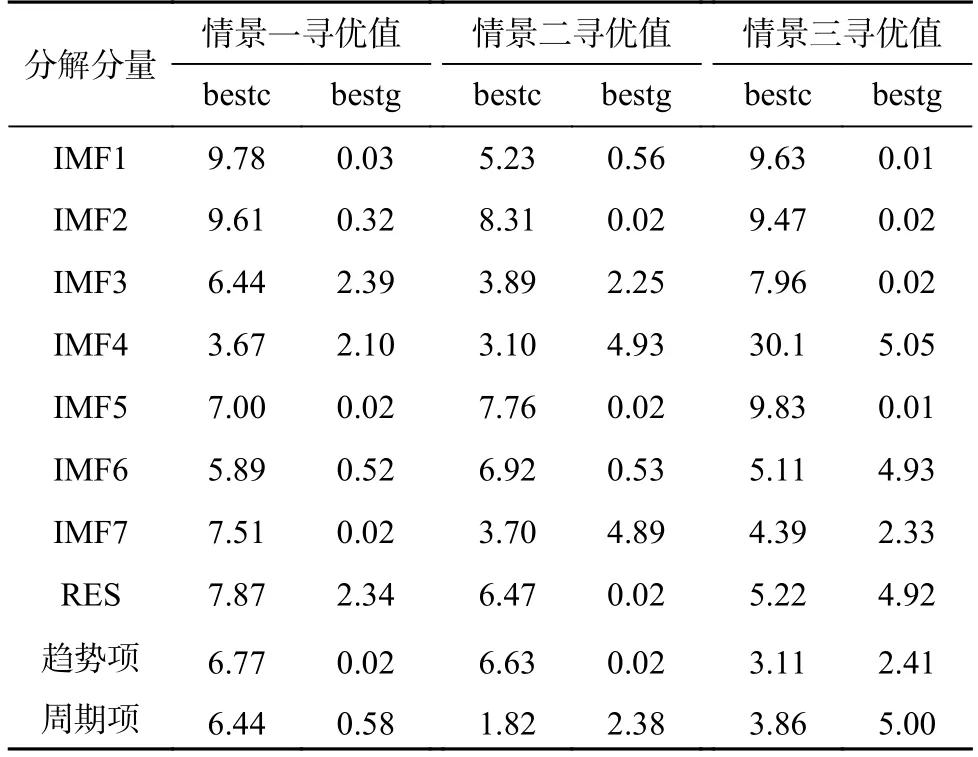
表6 GA 各分量SVR 模型超参数寻优值Table 6 Optimal value of hyperparameters for each SVR component model of GA

为验证构建模型预测效果，选用预测集数据对采煤工作面未来一段时期的绝对瓦斯涌出量进行预测。

由于文章篇幅所限，论文以情景三为例，对采煤工作面未来70 d 的瓦斯涌出量进行预测，其各分量模型预测结果如图6 所示，预测结果绝对误差见表7。

由图6、表7 可知，各分量预测模型预测效果较好，其预测曲线与实际曲线重叠度高、拟合优度好，平均绝对误差在0.000 7～0.724 7 m3/min 区间变化，维持在较低水平。

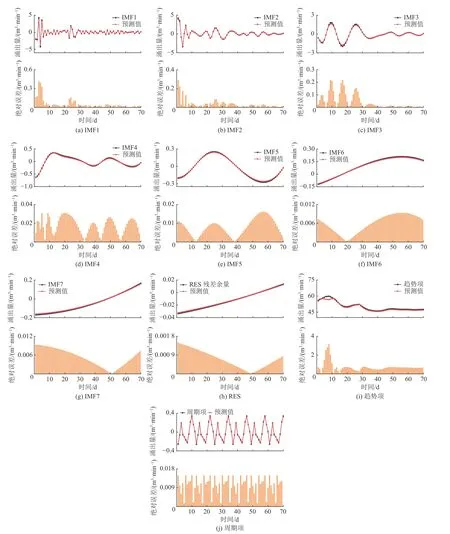
图6 时序分解各分量模型预测结果Fig.6 Prediction results of each component model in time series decomposition

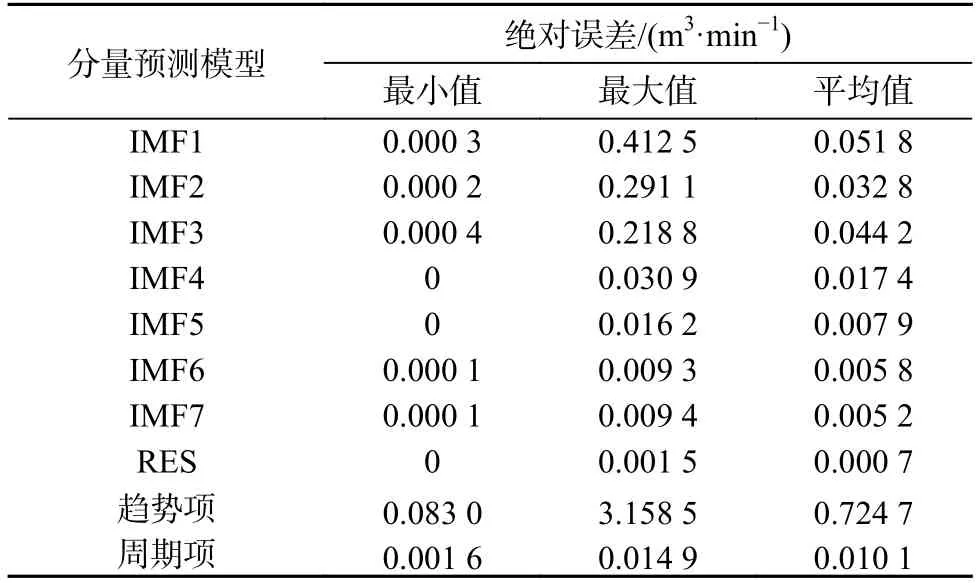
表7 各分量模型预测绝对误差Table 7 Absolute error of each component model

最后，对各分量预测结果进行叠加，重构得到最终绝对瓦斯涌出量预测值(图7)。由图7 可知，重构预测值曲线与实测值曲线近乎重合，拟合程度较高；其绝对误差为0.061 5～1.114 9 m3/min，平均0.385 2 m3/min；相对误差在0.13%～1.80%，平均0.73%，误差较小。较好地预测了采煤工作面未来70 d 的瓦斯涌出量走向趋势，验证了模型具有较高可行性。

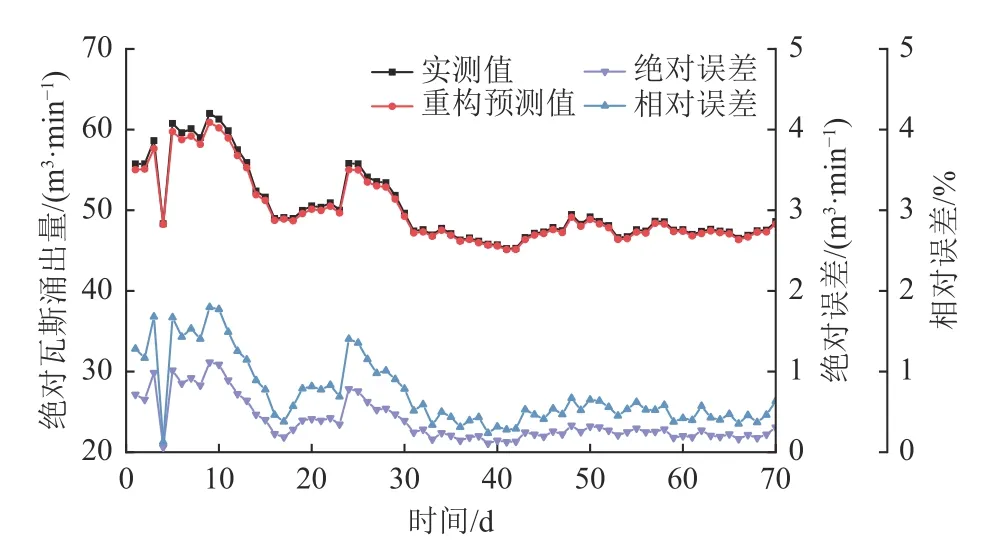
图7 时序分解模型预测结果Fig.7 Prediction results of time series decomposition model

3.3 预测模型对比分析

在3 种情景下对SEGS、EEMD-GA-SVR、GA-SVR和GPR 模型预测结果进行对比(图8、表8)。

由图8、表8 可知，SEGS 模型预测效果最优，验证了在EEMD 基础上引入STL 的必要性。情景一、二、三中SEGS 的R2精度分别为0.81、0.92、0.99；其中，情景三中SEGS 模型的R2为0.99，优于EEMDGA-SVR 模型的0.98、GA-SVR 模型的0.94。

图8 不同情景下模型预测结果对比Fig.8 Comparison of model prediction results under different scenarios

由表8 可知，训练集与预测集比例愈大，SEGS 模型优势愈明显。情景三中SEGS 模型的EMAP值与其他模型最大差值为1.32%；情景三中SEGS 模型的指标EMAP低于情景二中SEGS 模型的1.67、情景一中的2.93。

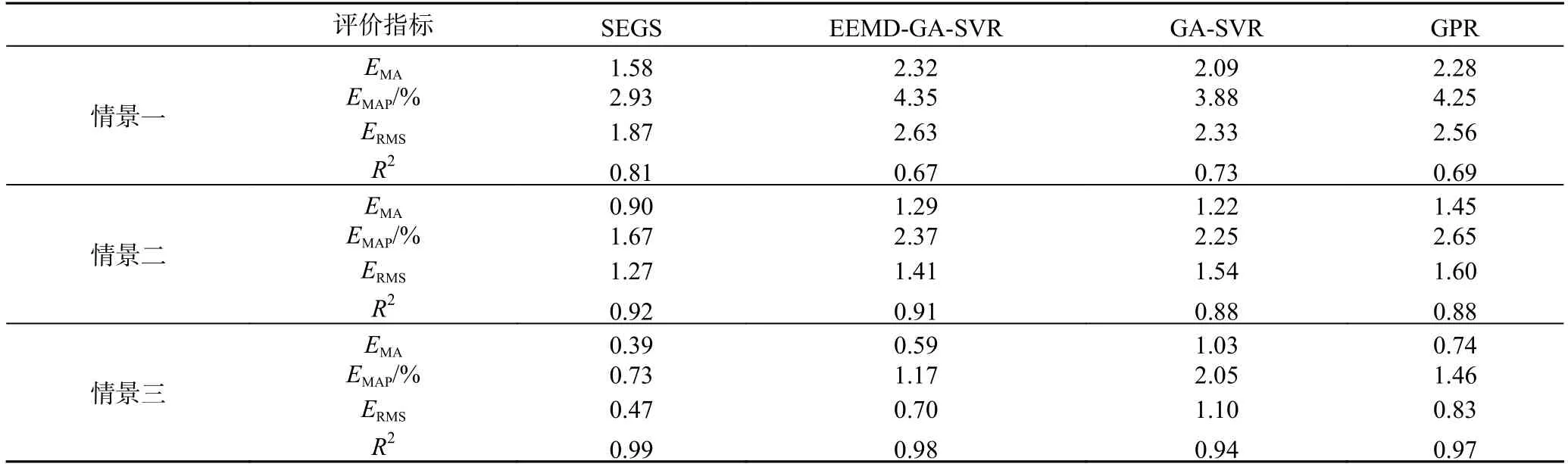
表8 各预测模型评价指标对比Table 8 Comparison of evaluation indicators for each prediction model

为验证瓦斯涌出量时间序列峰值点预测模型的准确性，依据图8 所标注峰值点绘制成图9，各模型峰值点预测误差对比见表9。由图9、表9 可知：SEGS 模型的峰值点预测效果优于对比模型。3 种情景下SEGS模型的峰值点相对误差、绝对误差均低于其他模型。

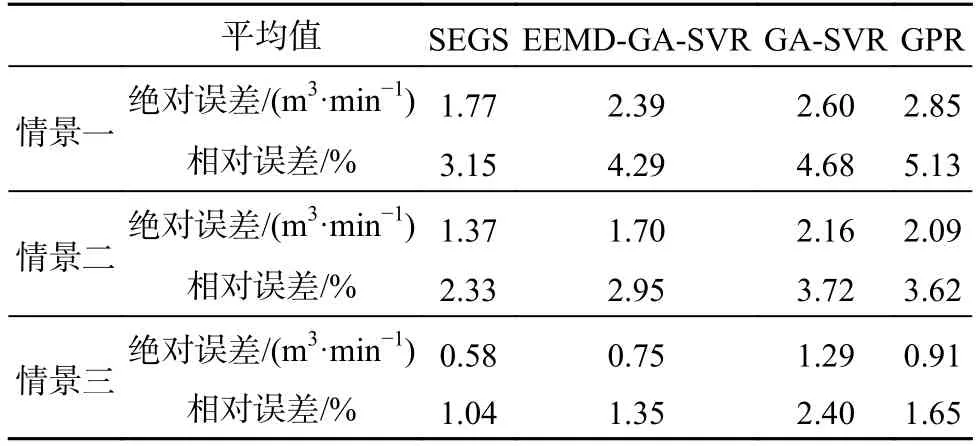
表9 各模型峰值点预测误差对比Table 9 Comparison of prediction errors at peak points for each model

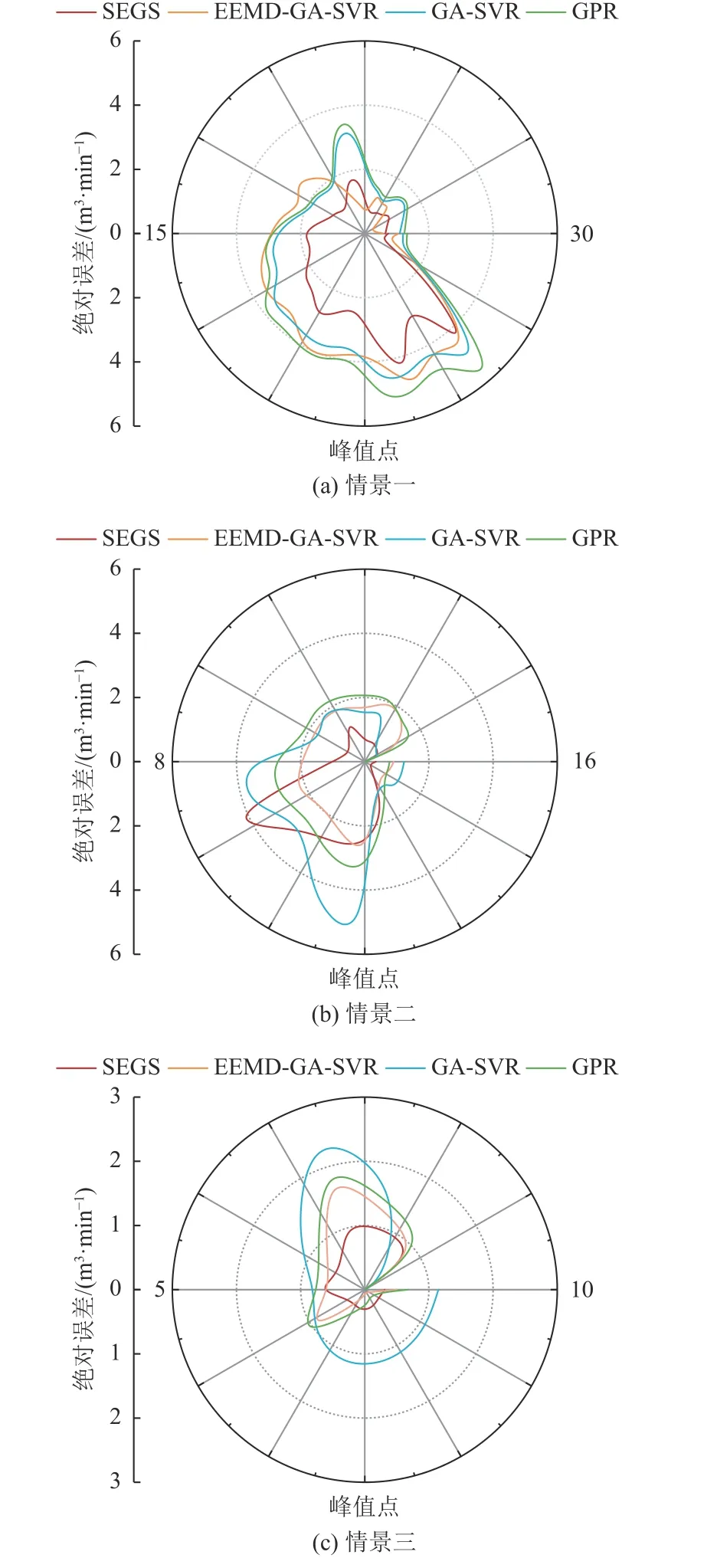
图9 各模型峰值点预测绝对误差Fig.9 Absolute error of peak point prediction for each model

综合3 种情景、4 种模型的对比结果可知，SEGS模型在预测精度及峰值点预测上优于其他3 种模型，证明了该预测模型在瓦斯涌出量预测领域的适用性。

4 结论

a.提出了采煤工作面瓦斯涌出量预测SEGS 模型，基于STL 和EEMD 将绝对瓦斯涌出量数据分解为趋势项、周期项和不规则波动项(IMFs 分量和残差余量)，通过GA 参数寻优后的SVR 建立了预测模型，该模型降低了数据复杂度，优化了平稳性，提高了预测精度。

b.通过对比分析多重、均值和线性插补方法精度，确定采用线性方法来进行缺失数据插补，并对6 组缺失数据进行处理，保证了数据结构的完整性。

c.分析了3 种不同绝对瓦斯涌出量预测集情景下，SEGS 模型、EEMD-GA-SVR 模型、GA-SVR 模型和GPR 模型的预测效果，结果表明SEGS 模型整体预测精度最高、峰值点预测误差最小(平均相对误差分别为3.15%、2.33%、1.04%)，证实SEGS 模型可有效应用于采煤工作面瓦斯涌出量预测。

d.受客观条件所限，本文采集的数据样本量有限，今后可针对其他矿井实际情况，进一步验证SEGS 模型的普适性；一些与采煤工作面绝对瓦斯涌出量相关的特征(如瓦斯浓度、风量等)尚未考虑，今后在数据允许的条件下可进一步探究。