基于多普勒非对称空间外差光谱测速的复合光程差相移解算方法*

彭翔 刘恩海 田书林 方亮

1) (中国科学院光电技术研究所,空间光电精密测量技术重点实验室,成都 610209)

2) (电子科技大学自动化工程学院,成都 611731)

3) (中国科学院大学光电学院,北京 100049)

非对称空间外差光谱技术是一种新型的超高分辨率遥感探测技术,基于其光通量大、体积小、精度高的特点,适用于深空环境下的高精度探测工作.也正因其高灵敏度的特性,使得实验中的各种细节因素都可能对测量结果造成干扰.本文从实验条件的角度,重点考虑条纹中心位置偏移、光照不均匀、高斯噪声等因素的影响,提出了复合光程差相移解算方法.经仿真计算和数据分析得出,相位标称点相对中心位置的偏移量会显著影响光谱测速的系统误差,而复合光程差相移解算方法能够在一定程度上平滑环境噪声和随机干扰造成的光谱测速精度误差.对于1%程度的高斯噪声干涉条纹图像,采用复合光程差相移解算方法能够将测速误差控制在5‰以内,使得非对称空间外差光谱技术能够更好地适用于空间光电精密测量的相关应用中.

1 引言

随着人类航天技术的发展,人造飞行器已经先后实现对月球、火星的探测,并逐步越走越远,而深空探测器的自主导航技术则直接决定了一个国家对宇宙的探测能力.所谓“自主导航”,主要需实现在深空环境中人造飞行器对自身的精确定位,即探测器在宇宙空间坐标系中分别沿x,y,z轴的线速度和方位角度的实时高精度测量.而随着人类对宇宙空间探测距离的拓展,主要依托大型地基望远镜的传统非自主测速方式的弊端愈发明显,高精度自主测速能力已经成为了新一代空间飞行器研发中无可回避的关键技术需求[1,2].

多普勒非对称空间外差(Doppler asymmetric spatial heterodyne,DASH)光谱技术是近年来一种新型的超光谱探测技术,由美国学者Englert 等[3,4]于2006 年首次公开提出,具有高分辨率、高灵敏度、无运动部件以及体积重量可控等优点.美国海军研究实验室于2010 年采用DASH 技术先后研制了基于630 nm-Ne 发射线的地基REDDI (the Redline DASH Demonstration Instrument)系统和机载ARROW(Atmospheric Redline inteRferometer for dOppler Winds)系统的原理样机,并获得了2—3 m/s 量级的测速精度,但由于地面实验环境条件的限制使得最大模拟速度仅有40 m/s 左右,使得其测速精度从相对误差层面存在争议,近年来的一些相关研究也是在受限的速度阈值范围内进行的局部方面讨论与调整[5−8].对于空间飞行器而言,实际运行速度在104m/s 量级以上(参考第一宇宙速度V1=7.9 km/s 和第二宇宙速度V2=11.2 km/s),远超地面实验室内能够生成和模拟的幅度;另一方面,由于实际工程环境中光能量分布的非均匀性和环境噪声等因素都会对干涉图信号造成影响,而灵敏度越高的测量仪器越容易受到干扰,使得DASH 光谱技术在一定噪声条件下对航天器运动状态的测速精度还需要进一步评估[9−12].

本文通过综合考虑实际工程中可能存在的中心位置偏移、光照不均匀、高斯噪声等因素对干涉条纹图像的影响,以及选取空间飞行器实际运行量级的多普勒速度进行仿真计算,同时提出了复合光程差相移解算方法.仿真计算结果表明,相位标称点相对中心位置的偏移量会显著影响光谱测速的系统误差,且复合光程差相移解算方法能够在一定程度上平滑环境噪声和随机干扰对光谱测速精度的影响.

2 DASH 光谱测速原理

DASH 光谱仪的原理结构如图1 所示,轴向光以角θ入射到光栅上,某一波数的光将以θ角沿原方向衍射回来,此波数称为光栅Littrow 波数.Littrow 波数σL的光经光栅衍射后的两出射波面都与光轴垂直,相位差为零;非Littrow 波数σ的光经光栅衍射返回后,传播方向与光轴有一小的夹角±γ,形成空间干涉条纹.反射光的两波面将存在夹角2γ,于是对应的光栅方程为

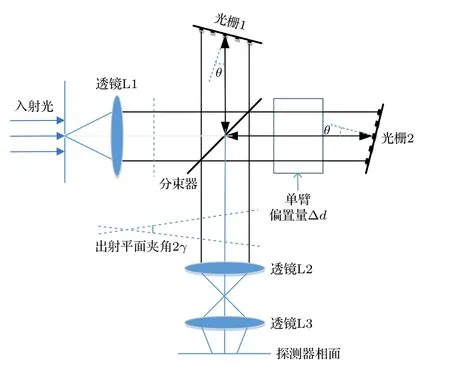
图1 DASH 光谱仪结构示意图Fig.1.Schematic diagram of DASH spectrometer.

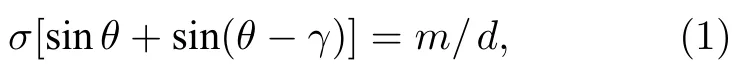
式中,σ为入射光的波数,m为衍射级(通常取m=1),1/d为光栅的刻线密度.

将探测器相面上干涉条纹的周期宽度记为D0,入射光波长为λ,则有

于是干涉条纹的空间频率记为kx,分别取Littrow波数σL和非Littrow 波数σ代入(1)式,可得到

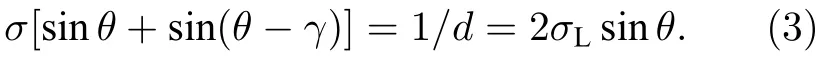
因光栅的选通特性使得γ为一小角度,将(3)式展开后得到

当入射光为B(σ) 时,所得到的干涉图为

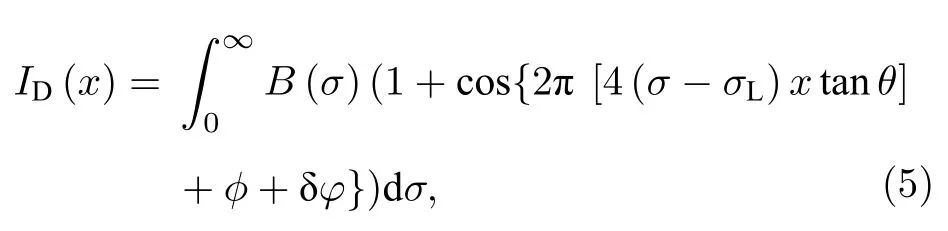
式中,B(σ) 为入射光谱密度,x为探测器上的像元位置坐标,ϕ为光谱仪引入的额外相位差,δφ为多普勒频移引起的相位差.经过傅里叶变换,分离出特征谱线后进行逆变换,计算相位,总相位为虚部与实部之比:

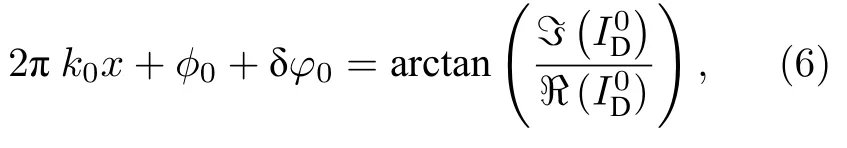
式中左边的前两项为需要定标的零速相位,可通过初始定标来确定;上下标0 表示选取图像中心x=0处作为测量解算的参考点.

DASH 光谱仪所采用的非对称式结构,是为了引入额外的光程差用于对信号波形的解算.由光信号的多普勒效应,速度调制引起的光谱微小频移将导致DASH 光谱仪相面干涉图样的相位变化.记入射光波段内光谱平均波长为λ0,此时探测器中心参考点的光程差为 ∆L=2∆d,条纹干涉级数为m;若光谱发生频移,条纹将向临近级次移动,级差为 ∆m,则有

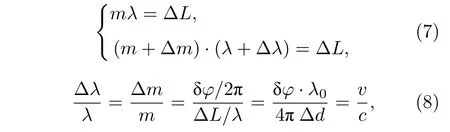
得到相位变化与径向速度之间的关系为

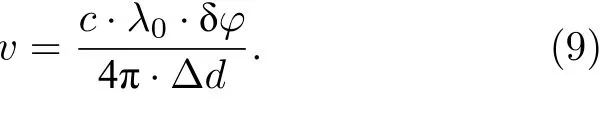
在相同环境条件下,测量由多普勒速度调制的前后两幅图像,计算对应像素点的相位差,就能解算得出调制速度值,此即为利用DASH 光谱仪进行遥感测速的基本原理.从(9)式可以看出,DASH光谱仪测量位置的光程差越大,所对应的相位偏差就越大,测量精度就越高,如图2 所示(f0表示频率,df为频率变化).但事实上,由于干涉条纹强度随光程差衰减的缘故,使得该光程差不可能无限大,可以设置一种效率函数来计算效率最大位置对应的最优光程差.

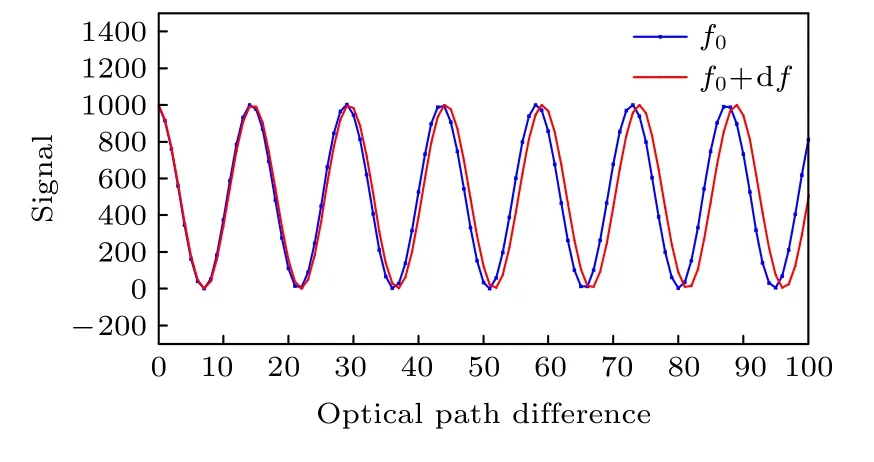
图2 相位差随光程差变化示意图Fig.2.Schematic diagram of phase changing with optical path difference.

DASH 所得条纹图像为光栅干涉,且探测器相面只能获取整段条纹的某一部分,如图3 所示.由于不同参数下所得的波形曲线具有不同的能量衰减,而振幅的变化一是会影响波形数据的解析精度,二是较低的能量幅值在AD 转换过程中会造成较大的分辨误差,因此在数据采集过程中需要事前反复调整各项参数以选择合适的采集数据段.

图3 探测器视场对应不同的干涉条纹数据段示意图Fig.3.Schematic diagram of different interference fringe data segments.

在探测器的视场范围内,较清晰的条纹部分大概率不会正好落在中心位置,如图4 所示,对其沿x轴截取某一行像素值序列即可作为输入信号波形进行解算.此时,从数据信噪比的层面考虑,固然是选择II 处亮度更高的位置作为锚定点进行解析,但II 处所对应的光程差则不再是 2∆d.本文中主要考虑中心位置偏移、光照不均匀和高斯噪声3 种因素对DASH 光谱测速精度的影响.

3 复合光程差相移解算方法

在多数的相关文献资料中,都默认了探测器靶面中心与DASH 光谱仪的主光轴严格对齐,相位计算时是直接套用(9)式进行处理.并且由文献[10]中的仿真数据可以看出,对于入射光谱分别采用高斯模型和洛伦兹模型仿真计算得出的最优单臂偏置量 ∆dopt的数值并不相同,使得按仿真参数制作的光学器件真正用于实验观测时,所获取的信号能量中心大概率不会对齐光轴.另一方面,仪器的装调误差也可能导致DASH 光谱仪的光轴并不完全对齐探测器相面的中心点.如图4 中I,II 段信号分别依据(9)式解算出的多普勒速度存在明显差异;I 段信号的均值误差约3%,标准差约18%;II 段信号的均值误差约56%,标准差约7%.并且由于高斯噪声的影响,单点的相位计算结果具有相当的随机性,使得单纯采用(9)式解算的处理方式不够稳健可靠.为了进一步提高处理算法的测量精度和鲁棒性,本文提出一种复合光程差相移解算(compound optical path difference phase-shift solution,COPS)方法.

图4 实测干涉条纹图像Fig.4.Measured interference fringe image.

由图2 可以看出,干涉条纹图像信号中各个像素点对应的相位差值都是不一样的;因此经多普勒速度调制前后的两幅干涉图像对应差分时,使用多个像素点得出的相位差计算均值要比单独选取中心点像素计算要更加可靠.在对称式空间外差光谱仪中,相面上干涉条纹的中心(主极大)就在光轴位置;而在非对称空间外差光谱仪中,由于额外引入 2∆d的光程差,使得干涉条纹中心产生偏移.假定在DASH 光谱仪成像面上干涉条纹的中心偏移量记为Xd,则其与中心光程差 2∆d的关系为

结合(4)式,解算得到:

由(11)式可以看出,探测器相面上距离中心位置的偏移与额外光程差具有 4tanθ的比例.因此在探测器相面上,中心之外的像素点光程差为

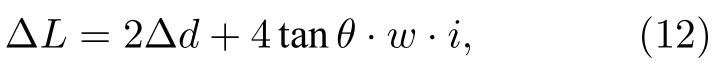
其中,w为探测器靶面的像素宽度,i为该像素对应中心光轴位置的偏离像素个数.

因此,更严格的DASH 光谱测速公式应该更新为

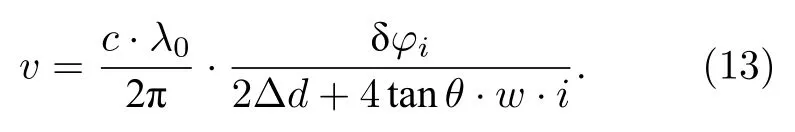
依据(13)式对干涉条纹图像中心区域的多个像素点分别计算两幅图像的速度差值,然后取平均数,即可在一定程度上减小数据截断误差和环境噪声的影响,提高DASH 光谱测速技术的处理精度,称之为复合光程差相移解算方法.

4 数据仿真实验

由于在地面环境中难以真实模拟宇宙空间中的真空低温环境,且无法产生稳定的宇航飞行器运动速度(∆v=10000 m/s 量级),故采用Matlab 仿真平台进行数据模拟计算.

4.1 波形曲线仿真

在不考虑噪声的情况下,定义图5 所示中心波长为411.3 nm、线宽为0.002 nm 的高斯型发射线信 号;DASH 光谱仪参数为光栅Littrow 角为14.318°,光栅密度为1200 线/mm,臂程差Δd为2 mm,探测器像素宽度为13 µm,采样点数N为1024;速度差值取 ∆v=10000 m/s .仿真计算得到的在空间域(探测器相面)上的信号波形如图6 所示,可见由于DASH 中的额外光程差导致干涉条纹中心位置偏移至约X=−4 mm 位置.

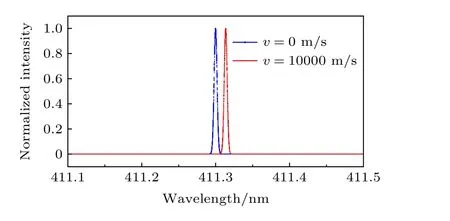
图5 发射线信号的多普勒频移示意图Fig.5.Schematic diagram of Doppler shift of emission line signal.

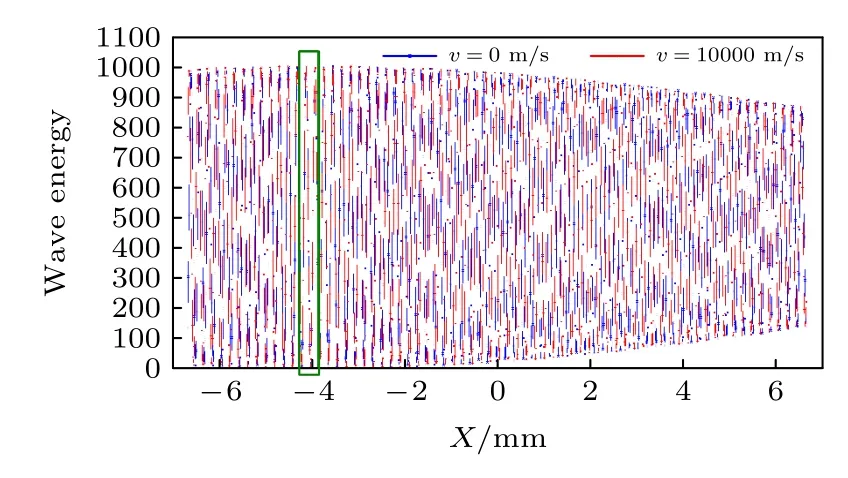
图6 多普勒频移对应的空间域波形变化示意图Fig.6.Schematic diagram of waveform change in spatial domain.

采用离散傅里叶变换(discrete Fourier transform,DFT)算法分别对两组波形信号进行解析,所得结果如图7 所示;其中蓝色曲线表示依据(9)式的传统计算方法得到的速度差值,红色曲线表示依据(13)式的复合光程差相移解算方法得到的速度差值.由图7 可看出,如果仅仅套用(9)式对多个采样点进行解算,则仅有中心零点位置可以获得正确的多普勒速度值,其余位置都会因为相位差的不同而出现明显偏差(每个像素间隔导致约32 m/s 的误差).而对于非零位置的采样点,使用(13)式进行计算则都可得到正确的速度值.由于传统DFT 算法存在测量不确定度,在本文所选的参数下,对中心点解算得到的速度值v1=9991.3 m/s,而对波形中心20 个点计算速度值取平均后得到v2=10000.8m/s,如表1 所列.可见复合光程差相移解算方法相对于传统单点解算的处理误差小了一个数量级.

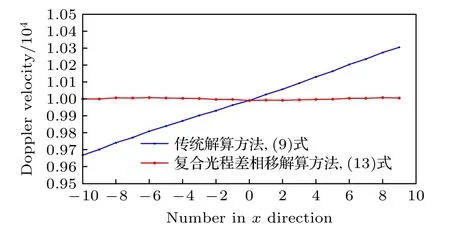
图7 基于DFT 算法的传统解算方法和复合光程差相移解算方法所得多普勒速度的对比图Fig.7.Comparison of Doppler velocity obtained from traditional solution method and COPS method by DFT algorithm.

表1 仿真计算所得速度值及误差Table 1.Speed value and error calculated by simulation.

4.2 条纹图像仿真

在实际工程中由探测器得到的是干涉条纹图像,背景环境中的高斯白噪声和探测器相面的能量分布非均匀性无可避免.故对图6 所示波形数据沿Y轴方向扩展得到条纹图像(宽w=1024,高h=512)之后,再加上1%的高斯噪声和标准差b=256像素的高斯曲线能量分布调制,得到如图8 所示的模拟干涉条纹图像,该图像基本上代表了实测中能得到的最佳状态.

图8 经调制后的模拟干涉条纹图像Fig.8.Modulated analog interference fringe image.

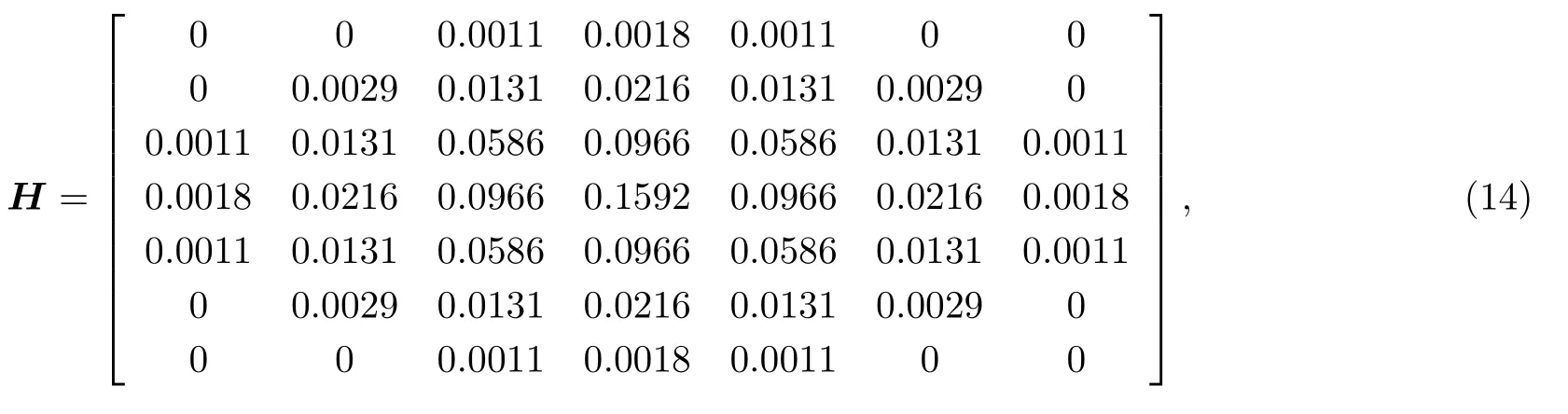
对模拟干涉条纹图像采用(14)式所示7×7 的高斯矩阵进行滤波处理,然后对其中心部分的256 行像素值分别采用传统DFT 算法和自适应频率跟踪(adaptive frequency tracking,AFT)算法[13]进行解算,所得速度差值如图9 所示.其中蓝色曲线为采用(9)式计算得到中心点速度值,红色曲线为采用(13)式解算中心20 点像素得到的速度平均值.表2 为不同算法及处理方法对干涉图解所得速度值对比.

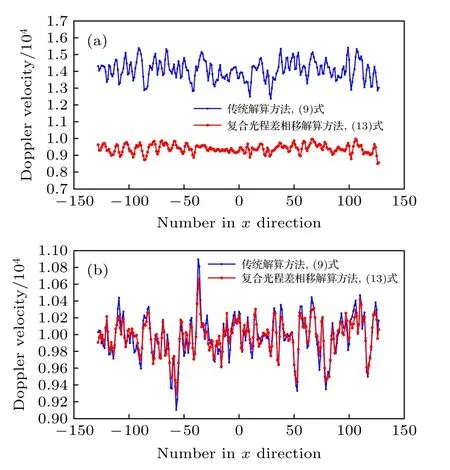
图9 多行像素波形序列的多普勒速度示意图 (a) 传统DFT 算法;(b) 自适应频率跟踪算法Fig.9.Schematic diagram of Doppler velocity of multi line pixel waveform sequence: (a) Traditional DFT algorithm;(b) adaptive frequency tracking (AFT) algorithm.

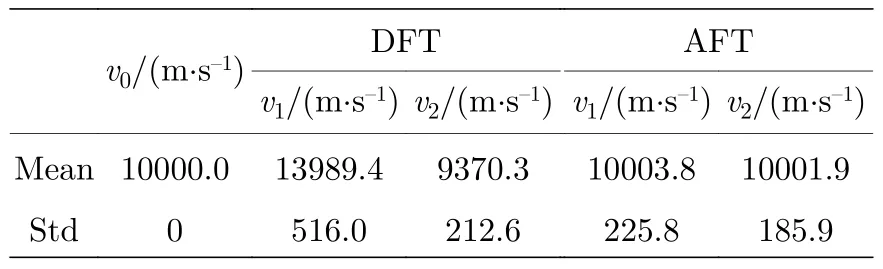
表2 不同算法及处理方法对干涉图解算所得速度值的对比Table 2.Comparison of velocity values calculated on interferograms by different algorithms and processing methods.

在图9(a)中,蓝色曲线表示的解算速度值与仿真设定值 ∆v=10000 m/s 之间产生了非常明显的偏差,而采用复合光程差相移解算方法的红色曲线仍然处于理论值附近;说明光照不均匀和高斯噪声对原有的仅以中心点像素为标称的解算方法影响非常大,而复合光程差相移解算方法能够很大程度地降低这种干扰.在图9(b)中,蓝色曲线的标准差AFT_std_center=225.8 m/s,明显大于红色曲线的标准差AFT_std_aver=185.9 m/s.由此结果一方面说明了环境噪声对像素能量波形曲线的解算会造成明显影响,另一方面说明了复合光程差相移解算方法能够在一定程度上平滑随机噪声,获得更高的处理精度.

由于高斯噪声的随机性,可以将如图8 所示的中心多行数据进行旋滤波和纵向叠加为一行数据来解算,用以平滑噪声的干扰程度[14].同样由于高斯噪声的随机性,每次重新加入模拟噪声后,解算所得的多普勒速度也存在偏差,因此可对多幅干涉条纹图像分别求取多普勒速度并计算平均值.对100 组干涉条纹图像进行自适应频率跟踪算法解算的结果如图10 所示,其中蓝色曲线为(9)式的原中心点相位解算方法,红色曲线为(13)式的复合光程差相移解算方法,可见复合光程差相移解算方法所得的数据标准差要明显更小,即处理精度更高.而沿条纹方向的数据纵向叠加,也能够在一定程度上降低高斯噪声干扰和图像光照不均匀对整体测量精度的影响.

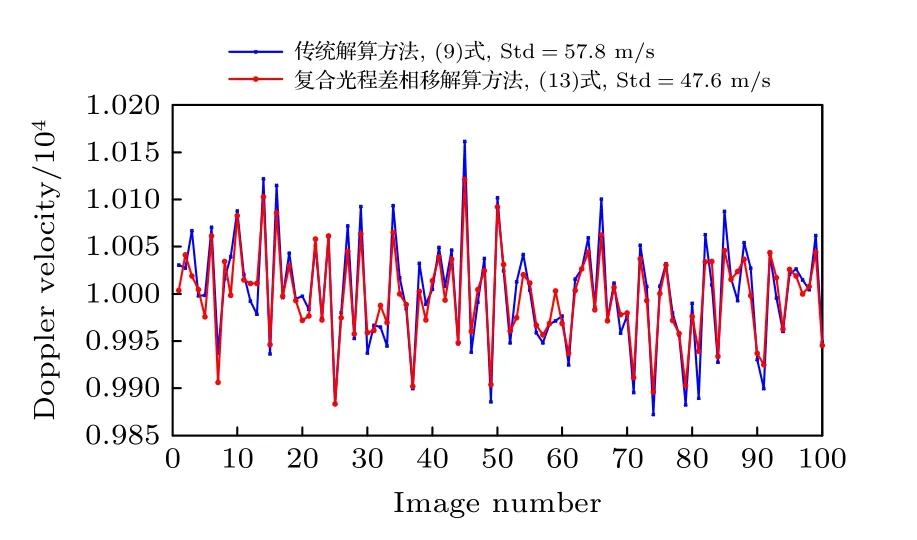
图10 两种方法计算100 组高斯噪声条纹图像所得多普勒速度差值的对比Fig.10.Comparison of Doppler velocity obtained from 100 groups of Gaussian noise fringe images calculated by the two methods.

5 实验数据分析

值得指出的是,尽管上述仿真数据中因模拟高斯噪声(1%强度)的影响导致了约100 m/s 量级的测速误差,远大于美国学者风场实验中得出的2—3 m/s 误差量级;其原因是本文的仿真实验中取标称速度差值为10000 m/s 并进行相对应的DASH参数配置,也远大于美国学者风场实验中所取的50 m/s 量级的待测速度标称值.故从误差/真值的比例而言,不能说明本文中的数据误差相对于当前已有技术的处理精度存在重大偏差或原理冲突.

复合光程差相移解算方法在DASH 光谱测速理论中,除在数据层面具有一定程度的处理精度提升作用之外,同时也指出了在实际工程测量中锚定像素位置偏离光轴中心的不可忽略性.如图6 中的蓝色曲线所示,单个像素偏离就会造成约0.3%的误差;而由文献[10]中的分析,高斯线型和洛伦兹线型光谱对应的最优光程差分别为和,代入本文的光谱仿真参数λ0=411.3 nm,∆λ=0.002 nm 和4.1 节DASH 设计参数,解算得出二者之间的靶面峰值距离约为360 个像素,将造成约108%的处理误差.由此说明在DASH光谱测速方案中,对采集数据进行分析解算时相位锚定点的选取非常重要;当锚定像素并不与系统光轴对齐时,需要计算偏离位置对应的光程差变化.

因此,本文提出的复合光程差相移解算方法相对于原有方法而言,不仅在理论模型层面能够降低测量随机性、提升数据解算精度,更是明确了DASH光谱测速过程中系统光程差与相位锚定点对齐的重要性.

6 结论

多普勒非对称空间外差(DASH)光谱技术是当前新型的遥感探测技术,具有体积小、灵敏度高等优点;因此在实际测量过程中,也得注意各个可能影响测量的干扰因素.在过去的研究中,默认了∆L=2∆d对应的探测器中心作为相位测量标称位置来解算多普勒速度.由于实际工程中的探测器像素尺寸远小于DASH 光谱仪的臂程差,且通常默认数据采集时图像中心具有最高的信噪比,致使在解算过程中容易忽略光程差变化的影响而直接套用计算公式.但通过本文的仿真数据分析表明,在应用于飞行器的深空探测自主导航领域,单点的随机误差和位置偏离造成的影响不容忽视.

本文从理论层面指出了干涉条纹图像中不同像素位置对应不同的光程差的区别,并提出了复合光程差相移解算的处理方法.一方面通过数据仿真和定量分析指出了非中心位置的标称像素偏离所造成的系统误差不可忽略,另一方面证明了复合光程差相移解算方法能够具有更高的数据解算精度和对高斯噪声一定程度的抵抗能力.经仿真实验数据论证,对于1%程度的高斯噪声干涉条纹图像,采用复合光程差相移解算方法能够将测速误差控制在5‰以内,使得非对称空间外差光谱技术能够更好适用于空间光电精密测量的相关应用中.