集成光量子计算的研究进展*
2022-12-31周文豪王耀翁文康金贤敏
周文豪 王耀 翁文康 金贤敏
1) (上海交通大学物理与天文学院,上海 200240)
2) (南方科技大学量子科学与工程研究院,深圳 518055)
3) (上海交通大学无锡光子芯片研究院,无锡 214000)
基于量子力学的叠加和纠缠等性质,量子计算具备超越经典计算机的强大计算能力.光子作为一种高效信息载体,具有传输速度快、操控性高及相干时间长的优点,是实现量子计算的一个理想物理平台.集成光量子技术,使得我们在微型结构上便能够稳定地实现光量子态的产生、处理和探测.近年来,随着新兴的集成光量子技术的快速发展,集成光量子计算的实验复杂度和规模在不断提高,并成功模拟和解决了复杂的物理和计算问题.为此,本综述总结了近年来集成光量子计算的技术进展,包括各类集成光量子实验平台,并讨论了基于集成光量子平台实现的量子行走实验范例.最后,我们亦简述了基于光量子行走而实现的量子算法和量子模拟的方案.
1 引言
20 世纪60 年代,Gordon Moore 提出了著名的摩尔定律(Moore’s Law)[1],该定律预测未来一段时间内,随着晶体管技术的发展,每隔18 个月计算机的计算能力将能够提升一倍.几十年来,摩尔定律非常贴切地反映了半导体产业以及集成电路芯片的发展趋势.当时间来到21 世纪,传统半导体产业以及经典计算机的发展越来越受到晶体管密度、集成电路能耗以及器件发热等集成电路工艺的限制,摩尔定律所描述的算力发展速度越来越难以持续.然而,人类对计算能力的追求脚步却从未停止.因此,近些年来,科学界在不断探索一种新的计算方式以进一步提升算力.
早在20 世纪80 年代,人们就发现随着问题规模的增大,求解多体问题所需的算力(比特数)呈指数爆炸式增长,使用经典计算机来模拟复杂的量子物理系统是充满挑战的[2].著名物理学家Feynman[2]认为可以放弃经典计算机,转而构建一台量子计算机,量子计算机中的每个量子比特(qubits)表示多体物理问题中的每个粒子状态,随着粒子数的增加,所需的比特数线性增长,这将能够解决我们所面对的计算爆炸挑战,量子计算的概念也因此诞生.随后,Peter Shor[3]在1994 年提出的Shor 算法以及Grover[4]在1997 年提出的Grover 算法(也被称为量子搜索算法)等方案都表明量子计算对特定的计算问题具有指数加速的优势.因此,人们相信量子计算有望在未来超越经典计算机为人类带来更高的算力.
一般地,量子计算模型可以被分为量子线路(quantum circuit)[5]及绝热量子计算(adiabatic quantum computation)[6],量子线路模型又包含一次量子计算(one-way quantum computing)[7]和拓扑量子计算(topological quantum computing)[8]两类特殊方案.
最常见的量子计算构建方案是量子线路.量子线路类似于传统的逻辑电路,为研究者提供了一种线路逻辑语言来表示不同的量子位、不同的逻辑操作以及不同顺序的应用.在量子线路图形化中,通常使用连线来表示量子位,并使用标记框和其他符号来表示这些量子位上的幺正变换U.在阅读量子线路图时,定义时间(通常被认为以离散时间步长发生)从左到右流动.量子线路可以将任意幺正变换U分解为一系列的量子门(quantum gates)操作,从而实现特定的量子计算功能,因此量子门的制备和实现也是量子线路方案中的实验重点.
一次量子计算由Raussendorf 和Briegel[7]于2001 年提出,该方案完全由对簇态(cluster state)的制备和对量子比特的测量组成,这些测量方式被对应到不同的量子逻辑电路上.由于量子测量属于破坏性测量,即测量同时会破坏其纠缠特性,因此簇态量子计算是一次性的、单向的量子计算机,由测量结果最终构成量子逻辑电路.
拓扑量子计算则是指在半导体结构引导的电子行为中观察准粒子行为,并进一步采用准粒子来进行编码计算.在拓扑量子计算中,制备马约拉纳零模(Majorana zero mode)是实现非阿贝尔任意子的重要方式之一,但马约拉纳零模体系存在两个待解决问题: 一是准粒子中毒,这在测量马约拉纳零模时会出现,并导致相干时间的缩短,从而会影响量子计算的性能;第二则是如何实现拓扑保护下的通用量子门.因此拓扑量子计算的实验实现依然非常困难.
中国科学技术大学郭光灿院士团队[9]采用光量子模拟器实验证明了基于仲费米子(parafermions)的通用量子计算的关键组件.研究人员首先通过操纵光子状态,实现了对应于仲费米子统计的 Clifford-operator Berry 相位.随后,他们通过证明仲费米子编码的量子态的互文性(contextuality),首次研究了拓扑系统中的量子互文资源.研究者通过光量子模拟器展现了仲费米子零模的编织统计和拓扑抗噪性质,从而为实现拓扑量子计算迈出了重要一步.
与量子线路不同,绝热量子计算是基于量子退火过程(quantum annealing)和绝热定理提出的,现已发展成量子计算标准电路模型的重要替代方案.绝热量子计算过程中,通过设置一个简单易求解的初态哈密顿量H0并随时间缓慢地向求解目标哈密顿量H1演化,系统的量子态会保持在能量最低的基态.由于量子隧穿效应,求解结果在量子退火过程不会被束缚在局域最优解内,能够通过隧穿效应离开局域解向全局最优解方向演化.
尽管已经有大量的理论和实验工作投入到不同体系下量子计算及量子算法的构建中,但通用量子计算(universal quantum computation)的实现仍然是非常困难的,这是由于无论以何种技术路线来实现通用量子计算机,都需要满足DiVincenzo[10]在2001 年为通用量子计算机提出的五项基本条件: 1) 一个可扩展的物理系统以及量子比特;2) 可以制备量子比特的初态;3) 量子比特具有足够长的相干时间,不易退相干;4) 能够实现通用量子逻辑门操作;5) 能够测量特定的量子比特.
由于这五项条件的约束,通用量子计算机的研制在当前的技术条件下并不成熟,为此在前期的研究探索中,不需要复杂的纠错机制,且相对容易实现的模拟量子计算(analog quantum computation)似乎是当下比较可靠的选择.模拟量子计算,是通过搭建目标指向的系统哈密顿量来对应特定的物理问题.短期内,通过模拟量子计算,已经在某些特定的物理问题上实现了对早期经典计算机算力的超越,如九章量子计算机[11]和悬铃木[12](Sycamore)量子计算机分别在玻色采样(Boson sampling)和随机线路采样(random circuit sampling)这两类问题上宣称超越了经典计算机的算力,这一里程碑式的研究成果标志着量子优越性(quantum advantage)不再仅仅停留在理论的预测阶段,已经迈进了实验证明阶段.
随着科学技术的发展,通用量子计算和模拟量子计算正加速迈向下一个时代,为此Preskill[13]在2018 年提出了含噪音中型量子计算(NISQ)的概念,这里的噪音是指当前对量子比特的操控仍然不稳定,例如对于量子门的不完美调控会降低实验保真度,对于整个系统而言是一种噪音;中型是指目前最大可操控的量子比特数仍然在100 个左右,离实现通用量子计算所需要的量子比特数还有距离.这一概念如今被广泛接受,表明量子计算机的发展还处于早期阶段,依然以突破和解决某一特定物理问题为主,离真正实现通用量子计算仍然有一定的距离.
如果把量子算法称之为构建量子计算机的软件,那对于算法的实验实现则是构建量子计算机的硬件.目前实现量子计算的硬件路径主要有超导、离子阱、光子、及核磁共振等[14],其中光子由于相干时间长、探测和操控方便,并且具有多个自由度等优势,是构建通用量子计算和模拟量子计算的理想平台,在接下来的部分,将展开介绍近年来光量子计算特别是集成光量子计算方面的研究进展.
2 光量子计算
量子计算的重点之一在于对量子比特的选取和编码,在光子、原子、核磁自旋、超导线路等可用于编码量子比特的系统中[14],光子由于不易退相干、速度快、易于操控等特性被认为是编码量子比特的理想载体[15,16].另一方面,尽管光子不易与环境耦合的特性保证了其鲁棒性,但也导致了光子之间很难有相互作用,只能通过线性光学器件来实现概率性的量子逻辑门,这对于大规模通用量子计算来说是一大瓶颈问题[17].虽然通用量子计算的实现仍然存在困难,但是以光子作为载体的模拟量子计算为量子计算打开了另一扇窗,通过构建系统哈密顿量来模拟可控物理系统,可以避免复杂的量子门操作和额外的量子纠错系统.
2.1 量子行走概述
在模拟量子计算中,量子行走(quantum walk)是一类被广泛研究的问题,它也被视为经典随机行走的量子版本.下面将介绍基于量子行走来实现模拟量子计算的研究和发展.
随机行走(random walk)的概念可以追溯到1905 年,由Pearson[18]提出,在随后100 多年的历史里,经典随机行走一直被用作一种计算方法和架构基础来解决复杂的计算问题,并在物理、化学、经济学及生物学等领域都有了进一步的发展和应用.与经典的随机行走的对应,1993 年Aharanov,Davidovich 和Zagury 三人[19]提出了量子行走这一概念,其本质来源于Feynman 的积分路径理论,并引入了关于多路径叠加的想法.
量子行走由于量子力学独特的量子叠加(quantum superposition)态特性,表现出向外扩散的弹道输运性质,在各类算法(如空间搜索算法、指数快速击中算法及图连通性算法等)中表现出了计算时间上的加速[20].在过去的十几年中,量子行走已经成为了一种常用的计算模型,其随计算规模展现出多项式级的计算时间复杂度,与之对应的经典算法往往需要指数级的运行时间.例如: Childs 等[21]在2003 年提出了一种用于图遍历问题的连续时间量子行走算法,相比于目前所有的经典算法,具备指数级的计算加速.正因如此,通过量子行走实现量子计算也是备受关注的研究领域.
2.2 量子行走的理论基础
基于量子行走的算法对经典算法的加速效果引起了广泛的研究兴趣,同时基于量子力学与其他科学领域的交叉研究,量子计算、量子算法、量子信息理论等新兴领域得到了蓬勃发展.与经典随机行走类似,量子行走可以被分为两大类: 离散时间量子行走[22]和连续时间量子行走[23].
如图1(a)所示,在离散时间量子行走中,时间是离散化的.离散时间量子行走给出了t时间步长之后特定位置i上行走粒子的量子概率振幅.这里的行走粒子可以是一枚量子硬币(quantum coin),在不具体测量硬币算符结果的情况下,硬币处于正面和反面的叠加状态:

图1 (a)离散时间量子行走,图片来自文献[22];(b)连续时间量子行走,图片来自文献[23]Fig.1.(a) Discrete-time quantum walks,the picture is reproduced from the Ref.[22];(b) continuous-time quantum walks,the picture is reproduced from the Ref.[23].

除上述硬币算符(coin operator)外,在离散时间量子行走中,还需引入平移算符(translation operator)来实现行走过程中行走粒子在位置上的变化.平移算符如下所示:

最终,通过硬币算符C和平移算符T的不断作用,可以得到n步之后的行走概率幅结果:
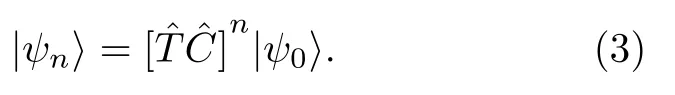
而在图1(b)中所展示的连续时间量子行走则无需硬币算符,也没有步长的概念.物理系统的状态用幺正变换的哈密顿量(Hamiltonian)来描述,系统经过了t时间的演化后,行走最终的概率幅结果由初态波函数和系统哈密顿量根据演化方程所决定:

无论是离散时间量子行走还是连续时间量子行走,其本质都源自量子态的叠加特性.迄今为止,这两类量子行走已经在多种平台上得以实现.
2.3 实现量子行走的实验平台
在实现量子行走的众多技术路线中,如光纤网络[24,25]、超导系统[26]、核磁共振系统[27]、囚禁离子原子系统等[28,29],基于光子的量子行走在实验实现上最为方便和稳定.在光量子行走的实验实现中,也存在不同的实验平台上,如传统光学平台、光纤平台以及近年来蓬勃发展的集成光量子平台等.
最早人们通过传统光学和线性光学器件来实现量子行走.在2005 年,Roldán 和Soriano[30]展示了仅使用线性光学器件就可以实现的二维量子行走的实验方案.该方案通过调节线性光学器件的参数可以实现不同的幺正变换,从而实现量子行走.
在光纤中,也有实验证明了量子行走实验的可能性.在2012 年,Schreibe 等[31]提出了一个二维量子行走的灵活实现方式.研究者展示了非平凡图结构上的可扩展量子行走.他们使用光纤网络实现了12 步长和169 个格点的相干量子行走.基于量子硬币算符,研究者能够在条件相互作用的二分系统中模拟纠缠的产生.进一步通过引入动态控制,这项工作还可以被用于研究强非线性或者是双粒子散射等效应.
上述两种实现量子行走的方式都是基于宏观光学器件完成的,宏观光学器件由于其灵活性和可操控性的特点在未来的量子信息实验中依然会扮演极其重要的角色.另一方面,随着实验尺度的增大,光学器件的数量会随着光学网络的复杂度而不断增长,这会在一定程度上阻碍实验系统的稳定性和规模大小,为此对于实验装置的小型化和集成化也是光学平台的发展趋势.随着集成光量子技术的发展,我们常使用硅基技术或光刻(lithography)技术来制备新一代的光子芯片,这些方法被统称为集成光子平台.
2008 年,Politi 等[32]在硅基二氧化硅平台上刻写了光波导线路,并实现了量子干涉和受控非门(CNOT)门,实验结果的高保真度证明了集成光量子的稳定性和可控性,这是集成光子平台里程碑式的工作.此后,更多的单量子比特和双量子比特的片上量子态制备和调控在硅基二氧化硅平台[33,34]以及激光写入二氧化硅平台[35−38]上得以实现.随着工艺和科学技术水平的发展,在2015 年,Carolan等[39]通过硅基平面波导结构展示了一个可编程的光学芯片并且基于芯片展示了一系列线性光学方案,包括量子逻辑门、量子纠缠门、玻色采样等实验.他们的实验成果进一步展示了可编程芯片在量子技术中的重要作用.
时至今日,一系列的光波导平台已经被应用于集成光量子系统的实验中,主要包括以下几类: 硅基平台(silicon-on-insulator)[40];硅基二氧化硅平台(silica-on-silicon)[41];飞秒激光直写平台[42];UV直写平台[43]和铌酸锂平台.
硅基平台(silicon-on-insulator)是一系列材料(硅,硅的碳化物和氮化物)的统称,如图2(a)所示.硅基平台的最大优势在于它与传统互补金属氧化物半导体(CMOS)作工艺相兼容,因此具有成熟的晶体管半导体制备工艺这一天生的优势.但是,硅基器件的波导尺寸较小,在与传统的单模光纤相连接的时候耦合损耗和传输损耗较大.通过对硅基波导的制备参数进行优化,这一缺点已经在实验上得到了改进[44].

图2 不同的集成光量子平台 (a)硅基平台,图片来自文献[40];(b)硅基二氧化硅平台,图片来自文献[41];(c)飞秒激光直写平台,图片来自文献[42];(d) UV 直写平台,图片来自文献[43]Fig.2.Different integrated optical quantum platforms: (a) Silicon-on-insulator platform,the picture is reproduced from the Ref.[40];(b) silica-on-silicon platform,the picture is reproduced from the Ref.[41];(c) femtosecond laser direct writing platform,the picture is reproduced from the Ref.[42];(d) UV direct writing platform,the picture is reproduced from the Ref.[43].
硅基二氧化硅平台(silica-on-silicon)是指在传统的单晶硅基底上制备一层二氧化硅层,如图2(b)所示,通过刻蚀的方式加工出波导,最后在最上层再制备一层二氧化硅层来保护波导.由于硅基二氧化硅平台在刻蚀波导的过程中需要掩膜版,因此制备工艺较为复杂.
得益于学术界和产业界的快速发展,硅纳米光子学已经被广泛用于量子光学实验之中.例如,由于硅具有很高的三阶非线性系数χ(3),因此可以用于产生量子光源.在2014 年,Harris 等[45]就在单个硅片上基于四波混频(SFWM)原理演示了关联光子对的产生,并且进一步对信号光子和闲频光子进行解复用和路由.由于该技术与CMOS 工艺兼容,因此可以重复制造,并且为最终将光源、处理器和探测集成在同一芯片上铺平了道路.
硅基平台另一个优点在于其集成度高,可实现单个芯片上数百个光学元件的集成.Sun 等[46]在硅芯片上展示了大规模二维纳米光子相位调控阵列(nano-photonic phased array).他们在576 µm ×576 µm 的芯片上集成了4096 个光学纳米天线(optical nanoantenna)从而实现主动相位调控.
除了硅基平台,激光直写平台也为集成光量子实验提供了可选择的技术路径.Davis 等[47]在1996 年首次提出了飞秒激光直写技术,如图2(c)所示.其基本原理是将高能量的飞秒激光聚焦于玻璃材料内部,由于聚焦区域的非线性能量吸收,会使得局部区域内材料的折射率发生永久性的改变,这种变化一般情况下为折射率的提高,从而使光在波导中以全反射的形式进行传输.在低脉冲能量的情况下,这种改性在许多玻璃材料内表现为平滑的折射率改变,而在高脉冲能量的情况下,激光诱导的改性可能包含周期性纳米平面等更多的结构.迄今为止,仍然没有飞秒激光与物质相互作用的完整物理模型,但研究表明可以将飞秒激光直写的加工过程大致分为三个阶段: 自由等离子体形成、能量弛豫过程和材料改性过程[48].飞秒激光直写技术的最大优点在于其三维加工的特点,传统的硅基波导被限制在一个二维平面内,而飞秒激光直写技术可以制备二维波导阵列,从而增加了物理维度和结构复杂度,为进一步探索更加复杂的物理问题提供了一种可靠的实验平台.
UV 直写技术由一个三明治二氧化硅结构构成,如图2(d)所示.二氧化硅层置于硅基底上,中间一层二氧化硅由于掺入元素锗(Ge)而具有光敏性,可以将连续UV 激光聚焦在中间层(Ge:SiO2)对其改性,并且通过移动基底来刻写不同的波导结构.UV 直写技术不需要硅基二氧化硅工艺中的掩膜流程,从而降低了制备波导的复杂度,但通过UV 直写制备的波导双折射通常较大,这不利于光子的片上极化编码.
除此之外,最近几年铌酸锂薄膜(LNOI)的商用化应用也受到了学术界广泛的关注和研究[49−51].铌酸锂(LN),也被称为“光子学中的硅”,这足以看出其在集成光子平台中的重要性.铌酸锂具有宽光学透明窗口,大的电光效应(electro-optical effect)和高玻璃化转变温度,这些优点对于加工工艺的稳定性和兼容性至关重要.此外,薄膜铌酸锂(LNOI)还由于其高固有电光效率、稳定性及可扩展制造技术的快速发展等,也成为了光通信、传感、量子信息等领域强有力的竞争者.薄膜铌酸锂平台继承了传统体铌酸锂器件所有的材料优势,并且以更小的占用空间、更宽的带宽和更低的功耗,凸显了其相比于其他材料的优越性,也是当前集成光子平台的候选者之一.
总体来看,对于实验上不同系统、不同材料、不同波导几何形状和制造技术、不同实验平台和波导加工方式各有其特点和优势.研究者根据实验所要求的集成度、调制速度及制造成本等因素,通过选取合适的实验平台,可以开展不同的量子信息实验.
2.4 基于集成光量子平台的量子行走实验实现
集成光子学作为一个新兴的科研平台,可以执行各式各样的量子信息任务,例如量子行走、玻色采样、拓扑光子学实验等,是实现大规模量子信息实验的可靠平台.由于集成光子平台集成度高、兼容性好的特点,有利于拓展量子信息实验的规模,并且已经提供了实际的应用场景,例如芯片量子密钥分发[52].
2008 年,Perets 等[53]首次展示了基于一维波导晶格实现的量子行走.波导晶格具有易于大规模构建并且光子在其中不易退相干的特性,是研究量子行走和量子算法理想且多功能化的实验平台.研究者通过实验观察了100 个格点的大型一维量子行走并且从理论上研究了包括弹道传播、无序性和边界相关等量子行走效应.
实现大规模量子行走的目的在于将其与复杂物理系统相对应,从而解决实际的物理问题,为此目前的研究工作主要聚焦在于拓展物理系统的复杂化.实验上,对于增加系统演化的复杂度,扩展其物理维度和增加初态光子数量是两种有效的研究方向.
2010 年,Peruzzo 等[23]在SiOxNy芯片中集成了21 根连续渐逝耦合的波导并第一次实现了关联光子对的一维量子行走实验.他们观察到的量子关联性最大达到了76 个经典极限的标准差的破坏并且发现量子行走中的量子关联性依赖于注入态的选取.实验结果为在指数增长的更大的态空间编码信息提供了有效的方法.
更进一步,在2017 年,Harris 等[54]利用硅波导,在纳米光子平台实现了由88 个通用分束器组成的可编程纳米光子处理器,其中每一个分束器都可以通过调控振幅和相位,从而在微秒时间尺度上进行编程.基于这个可编程处理器,他们研究了环境辅助的量子传输机制以及静态无序离散时间系统中的 “quantum goldilocks” 机制.这种低损耗和高保真度的可编程处理器是实现量子模拟实验的可靠平台.
尽管在调控技术和可编程速度上不如硅基波导成熟和快速,但得益于三维制造的优势,激光直写技术有利于在二维波导阵列上研究量子行走及其传输特征.Owens 等[55]在2011 年研究了椭圆形波导阵列中双光子态的演变,如图3(b)所示.研究者利用超快直写技术在高纯度熔融石英芯片中制造了椭圆形波导结构,并利用相干光态层析来特征化光子芯片,进而使用特征化结果来预测时间上不可区分和可区分的双光子输入态之间的明显差异,并将特征化结果与实验结果相比较.这项工作提出了在三维波导结构中模拟相干量子现象的可行性.
Sansoni 等[56]研究了不同的粒子统计(玻色子和费米子)对离散量子行走结果的影响.研究者利用偏振纠缠模拟了非相互作用玻色子和费米子的聚束和反聚束特征.实验中利用飞秒激光直写技术引入了包含波导电路的新型三维几何结构.三维结构如图3(c)所示,可实现精确的偏振无关行为,同时又保证了对相位和平衡性的显著控制.
Poulios 等[57]同样使用飞秒激光直写技术构建了光子晶格,并在图3(d)中的“十字”结构中实现了关联光子的准二维量子行走.关联探测事件展现出高对比度的量子干涉现象和独特的复合行为,包括量子行走粒子在“十字”结构之间的强关联性和在结构内部的独立性.
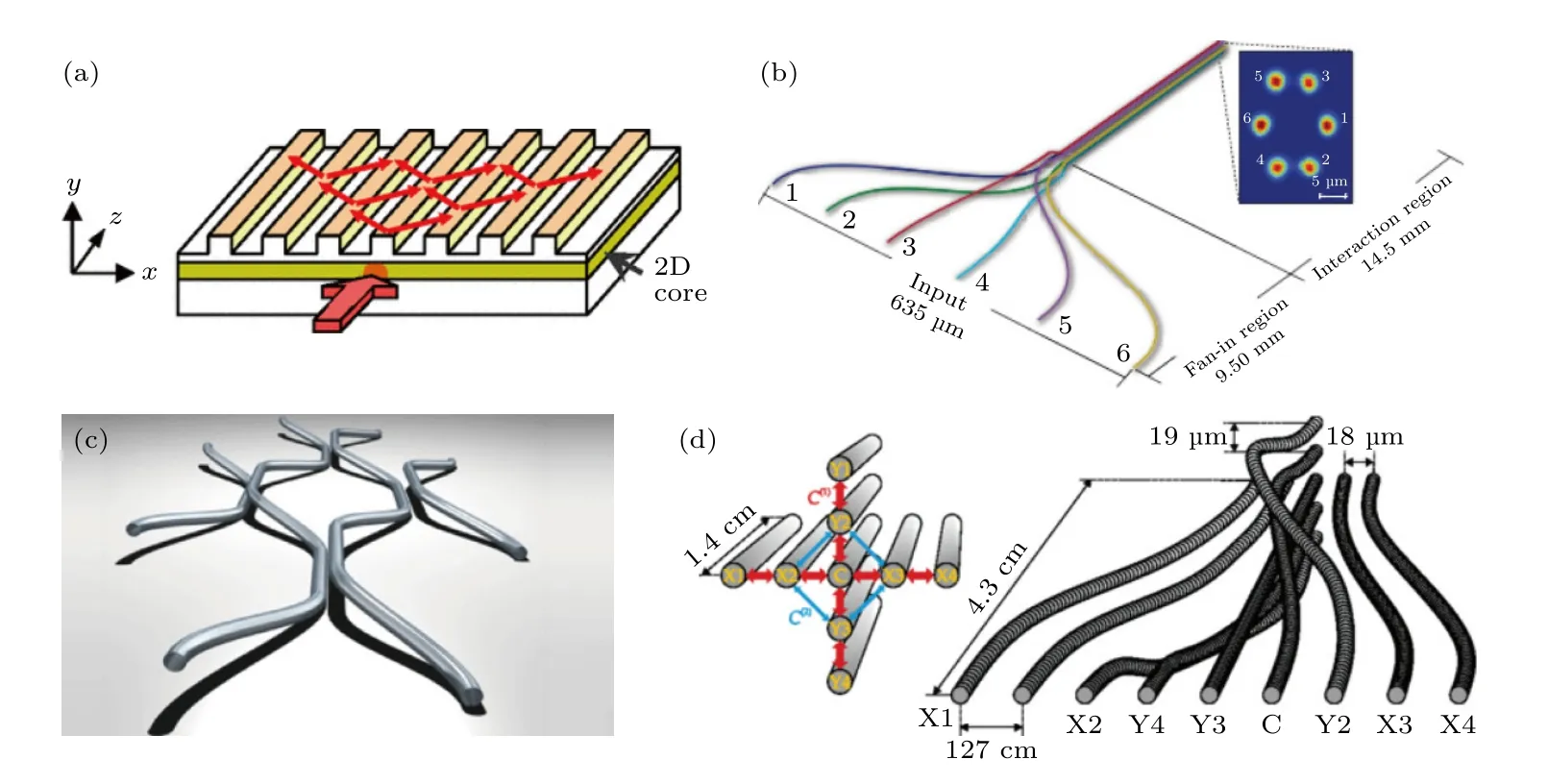
图3 不同波导结构图 (a) 一维波导阵列,图来自文献[53];(b) 椭圆型波导阵列,图来自文献[55];(c) 三维波导结构,图来自文献[56];(d) “十字”波导阵列,图来自文献[57].Fig.3.Different waveguide structures: (a) One-dimensional waveguide array,the picture is reproduced from the Ref.[53];(b) elliptical waveguide array,the picture is reproduced from the Ref.[55];(c) three-dimensional waveguide structure,the picture is reproduced from the Ref.[56];(d) “cross” waveguide array,the picture is reproduced from the Ref.[57].
Tang 等[58]利用光波导阵列的几何结构实现了超大规模二维连续时间量子行走实验.研究者利用飞秒激光直写技术构建了一个大规模的三维波导结构,如图4 所示,并在光子芯片中集成了一个二维方形格点,格点数高达 49×49 .他们利用预报性单光子和单光子成像技术展示了空间上二维量子行走的演化结果;通过观察量子行走的弹道演化模式和方差分布分析了量子传输特性,实验数据与模拟结果相吻合.Tang 等[58]进一步解释了二维量子行走相对于一维量子行走独特的瞬态性质.将这项研究结合缺陷和无序控制,可能为经典情况下棘手的物理问题提供了新的解决方案.

图4 光子芯片上的二维量子行走.图来自文献[58]Fig.4.Two-dimensional quantum walks on a photonic chip,the picture is reproduced from the Ref.[58].
该课题组在2021 年,进一步由Jiao 等[59]利用关联光子对,在三角形格点中实现了二维空间上的双光子量子行走.研究者将实验对应到了一个 37×37 的高维态空间.这种双光子二维量子行走突破了单粒子演化的物理限制,实现了更大态空间中的信息编码和高维图的构建,有利于量子信息的处理.如图5 所示,通过在芯片和二维光纤阵列之间构建起点对点的寻址,能够同时探测600 多个非经典干涉现象,进而观测到了违背经典关联的量子关联特性,并且超出了经典关联57 个标准偏差.这项工作为大规模二维量子行走提供了新的思路.
除了直接扩展空间维度和引入更多的光子数,引入合成维度同样有助于在低维度上解决复杂的计算问题.Ehrhardt 等[60]将光子的偏振维度引入到量子行走实验中,如图6 所示.通过具有特定双折射的复杂波导电路中光子对的空间自由度和偏振自由度的混合作用以实现合成维度,从而实现了与三维网络相关的激发动力学.该实验可被应用在复杂、高度连通的图形上以进行多粒子量子行走的实验探索,并且为进一步开发费米子动力学在集成量子光子学中的潜在应用铺平了道路.
3 集成光量子计算应用
3.1 基于量子行走的算法和应用
如前文提到的,量子行走作为一种算法工具,在生物学、物理学、经济学及计算机学等众多领域都具有广泛的应用前景,可以实现不同的量子算法和模拟传输过程[61−64].
Kendon 和Tamon[65]介绍了有限图上量子行走中的完美态传输.研究者利用不需要局部变化动态控制的结构进行传输,从而简化了传输设计并减少了出现错误的概率.量子行走也被用于模拟生物学中的光合作用.如图7 所示,光合作用系统的能量转移过程能够显示量子效应,然而其量子动力学过程与激子(exciton)转移效率的相关性在很大程度上是未知的.为此,Mohseni 等[66]提出了一个理论框架用于研究量子干涉效应在与热浴相互作用的分子阵列的能量转移动力学中的作用,进而模拟了光合作用过程中的能量传输过程.Gamble 等[67]则从图同构问题出发,研究了描述非同构情况下的单粒子和双粒子的量子行走动力学演化的格林函数,进而证明了存在相互作用的粒子可以区分非同构图,而非相互作用的粒子则不能区分.

图7 量子行走用于模拟光合作用中的能量转移过程,图来自文献[66]Fig.7.Quantum walks in photosynthetic energy transfer,the picture is reproduced from the Ref.[66].
除了模拟量子计算之外,实现通用量子计算一直是量子计算的最终目标,在2009 年,Childs[68]就展示了通过量子行走来实现通用量子计算的方式.在量子计算的一些早期工作中,Feynman[2]展示了如何使用与时间无关的哈密顿量来实现通用量子计算.Childs 则表明即使哈密顿量被限制为低维度图(graph)的邻接矩阵,通用量子计算的实现仍然是可能的.因此,量子行走可以作为一种通用计算方式,任何量子计算都可以被编码在某个图表达中.而在2013 年,Childs 等[69]进一步证明了多粒子量子行走也可以被用于实现通用量子计算.他们的研究成果表明构建一台可扩展的量子计算机并不需要时间无关的调控.
量子行走和量子快速到达算法(quantum fast hitting)在粘合树问题上展示了其比经典随机行走更快的击中速度[70].这体现了量子行走在加速模拟和优化任务方面具有强快的计算速度.但是由于其节点数量随网络深度指数级增加,其实验实现非常具有挑战性.
Tang 等[71]在2018 年提出了一种具有多项式增加节点数量的替代结构.他们使用飞秒激光技术以几何可扩展的方式在光量子芯片上制备了这种结构,并在多达160 个节点和8 层深度的图上展示了不同结构的量子行走过程.实验结果证明了量子加速击中效应,并且最佳命中时间和网络深度之间成线性关系.Shi 等[72]在2020 年利用粘合二叉树的一维等效结构,制备了层数从二层到十六层,叉数从二叉到五叉的光量子芯片,并在芯片上展示了量子快速到达算法.实验结果同样表明最优量子到达效率相对于经典随机行走而言可实现指数级的提升.这表明专用量子算法在快速到达问题上具有指数加速优势.
与非逻辑树问题(NAND tree)也是一类具有量子加速优势的问题,其结构如图8 所示.Wang 等[73]通过结合量子滑梯以及与非树,在集成光子芯片上实现了量子与非逻辑.与分子系统相比,激光直写集成芯片系统在集成度和扩展度上有巨大优势.此外,这项工作中的平衡树结构可以很容易推广到不平衡的与非算法,这将可应用于二人对策问题.此外由于与非门的通用性,这使得推广量子与非门表示任意的布尔函数成为可能.

图8 与非逻辑树问题,图来自文献[73]Fig.8.Nand tree problem,the picture is reproduced from the Ref.[73].
3.2 玻色采样及量子霸权
除了标准量子行走以及相关的应用以外,还有其他一些量子计算任务也是量子计算领域的研究热点,其中玻色采样(boson sampling)就是一类被深度研究的量子计算问题,玻色采样理论和实验的提出源于对量子优越性的实验实现.由于通用量子计算的实现目前仍然存在巨大挑战,为此制定一个中期可实现的里程碑目标是必要的,这个目标被称为量子优越性(quantum advantage),也被称为量子霸权.玻色采样实验由于其实验上易实现,具有明确的计算复杂度理论等特点,是实现量子优越性理想的平台.
玻色采样实验由Aaronson 和Arkhipov[74]在2011 年提出.它的实现方法是将n个全同玻色子注入到n×m的线性干涉网络中,经过多光子干涉过程后出射,并被单光子探测器接收.玻色采样实验的主体只需要单光子量子光源、线性干涉器件和单光子探测这三个部分,并且这些器件以当前的实验技术都是可以实现的.
时至今日,已经有大量的玻色采样实验及其变体被实现,例如随机散射玻色采样(scattershot boson sampling)[75]、高斯玻色采样(Gaussian boson sampling)[76]、时间戳玻色采样(timestamp boson sampling)[77]等,他们都旨在进一步降低玻色采样实验的难度并提高计算复杂度.在2020 年,九章一号[11]通过超低损耗,集成化的多摸干涉仪和外置的高亮度量子光源,构建了76 个光子,100 个模式的量子计算原型机,宣称通过高斯玻色采样实验实现了量子优越性,开起了玻色采样实验的新阶段.随后在此基础上九章二号[78]进一步构建了113 个光子,144 个模式的量子计算原型机,并且相比于九章一号实现了相位可编程功能,使得与高斯玻色采样实验相关的广泛应用成为可能.除此之外,通过在实验光源或者是线性干涉网络中构建环路,Gao 等[79]以及Madsen 等[80]通过不同的方式展示了基于玻色采样实验的量子优越性.
3.3 拓扑光子学
与此同时,量子行走本身也是研究其他物理现象的量子模拟平台.基于光量子行走平台,拓扑光子学的研究吸引了广泛的关注,该方向的探索为新物态及新材料的实验研究提供了便利的实现方式.
基于前面提到的飞秒激光技术,研究者能够实现对二维拓扑材料的模拟与实现.2013 年,Plotnick等[81]利用飞秒激光直写平台构建了光子石墨烯结构,并成功观察到石墨烯结构的边界态.同一时期,Rechtsman 等[82]同样基于飞秒激光直写波导提出并实验实现了一种无外场和无散射边缘传输的光子拓扑绝缘体,在晶格边缘观察到了可见光的拓扑保护传输.
随着基于集成光量子技术与拓扑物理结合的拓扑光子学的发展,研究者不仅仅局限于探索拓扑物态的方向.与此同时量子拓扑光子学的概念也被提出,该方向则是探索量子信息与拓扑光子学的结合,研究出基于拓扑材料实现的拓扑保护的量子态.
光子稳定、快速、具有远距离传输的能力,使其成为量子信息的理想载体.然而,对于芯片化的应用,光子不可避免地会与周围的介质相互作用,并且甚至可能会因为损耗而丢失.对于纠缠光子来说情况会更加复杂,光子之间的非经典关联可能会因此消失.结合拓扑晶格特性,将拓扑边界的保护机制扩展到量子体系中,利用拓扑结构直接保护物理演化系统中的量子特性.同时结合集成光子芯片的集成性和可控性,片上拓扑边界态有可能提供一种有效保护量子性质的替代方法.
Wang 等[83−85]先后实验证明了拓扑晶格可以为单光子、关联光子以及纠缠光子提供保护,使其免受耗散和无序引起的退相干.在实验中,研究者展示拓扑边界态保护单光子对抗环境噪声引起的退相干的能力.而在对互关联和柯西-施瓦茨不等式(Cauchy-Schwarz inequality)违背程度的测量则表明,量子关联双光子态在拓扑非平庸边界态中可以被很好地保持,在体态中则不能.此外,实验还证实了这种拓扑保护对两个光子的波长差异和可分辨性具有鲁棒性.
同一时期,Blanco-Redondo 等[86]实验证明了双光子态的拓扑保护,研究者在具有非平凡拓扑的纳米光子晶格中产生了能够稳定传输的双光子态.同年,Barik 等[87]证明了单个量子发射体和拓扑鲁棒光子边缘态之间的耦合,Tambasco 等[88]报道了在单个光子波导阵列中两个单光子拓扑边界态的高可见性量子干涉.Wang 等[89]实验证明了空间纠缠双光子态的拓扑保护.Mittal 等[90]在二维谐振器阵列组成的拓扑系统中实现了能够产生不可分辨光子对的可调谐源.
近年来的一系列工作将拓扑相的保护机制扩展到量子体系中,实现对量子关联保护的方法是一种新的保护量子的途径.该方向的研究正是在集成光量子与拓扑光学紧密结合下实现的新方案.我们相信随着更多研究方向的交叉探索,光量子计算的边界将能够得到进一步的拓展,交叉学科的探索将推动光量子计算的稳步前进.
4 总结与展望
在当前的技术条件下,通用量子计算机可操控的量子比特数目依然有限.此外在量子线路中往往需要高精度量子门的制备以及额外的量子纠错系统,这对于目前通用量子计算机的构造依然存在巨大挑战.发展模拟量子计算是目前量子计算研究中的过渡期.量子行走就是一类被广泛研究的模拟量子计算问题,而光子由于操控性高、相干性好及速度快等特点,是光量子计算实验中可靠的信息载体.本文介绍了集成光量子技术的发展以及基于当前技术平台实现的集成光量子计算研究进展.依托于近年来集成光量子平台的快速发展,光量子计算迈向了集成化、小型化的阶段,而其实验规模和光量子比特的数量也是逐年快速增长.在未来,随着集成光量子技术的进一步发展,伴随可操控量子比特数量的增加以及配套的纠错系统的实现,将能够构建更大规模的多体物理系统,进一步扩展量子算法可实现的规模,迈向光量子计算领域的全新阶段.
