光栅尺被动隔振系统建模与仿真分析

邓宏光，陈新度，王 晗，梁忠伟

（1.广东工业大学机电学院，广东 广州 510006；2.广州大学机械与电气工程学院，广东 广州 510006）

1 引言

光栅尺作为高精度位移传感器广泛应用于数控系统，宏微平台等精密位移控制系统和工业测量领域[1−2]。目前以螺栓直接固定尺体于运动平台的凸台基面的安装方式[3]，使得运动平台的振动与冲击直接作用于光栅尺[4]。随着微纳加工的发展，运动平台振动对光栅尺精度的影响日益凸显。目前针对光栅尺振动的研究较多集中于数据后处理，如通过对测量数据信号进行误差补偿处理等方法[5]降低振动对测量精度的影响等，但无法从根本上消除振动对光栅尺测量精度的影响。

光栅尺一般为截面不变的均匀长条状尺体，其长度取决于安装平台的运动范围，对于大尺寸的数控机床系统，其长宽比更大。受逼仄的安装空间限制，光栅尺难以采用普通隔振机构。切削加工时，机床振动难以避免，非平稳切削、切削颤振[5]等更恶劣工况甚至引起机床自激振动[6]。故亟需研究其在振动与冲击工况下的力学特性并探索隔振设计，减低运动平台振动对光栅尺测量精度的影响。基于上述分析，结合光栅尺的结构特性，建立了5自由度动力学模型并进行了解耦分析，得到系统传递函数。通过频率响应和阶跃冲击仿真分析了机床振动对光栅尺的精度影响，为具体的隔振设计提供理论依据。

2 光栅尺动力学建模

光栅尺几何特征通常为长条状、对称且质量均匀，其质心通常与几何中心重合。以某数控机床工作台上平行于X轴导轨的光栅尺为例，该光栅尺X方向与机床X轴导轨平行，Y方向平行于Y轴导轨，与X向正交，Z方向平行于Z轴导轨，垂直于工作台竖直向上，即所定义的光栅尺坐标系与机床坐标系一致。其余安装位置的光栅尺分析时亦可参考建立类似的坐标系，不失一般性。

光栅尺在上述X、Y、Z3个平动自由度均易受机床振动影响，其中，X方向平动自由度的振动直接影响读数头读取的光栅条纹位置，是误差敏感方向；Y、Z此2个平动方向自由度的振动主要影响光栅尺体与读数头的动态间距，即影响读数头的光学焦距。绕Y、Z轴回转方向即Ry，Rz2个回转自由度由θ，φ描述。由于光栅尺条状外形长边与X轴同向，考虑其安装时平行于导轨装于机床滑台上，可理解为光栅尺与机床滑台在绕X轴回转方向的刚度极大，故此方向振动可以忽略。

由上述分析，可建立光栅尺5自由度动力学模型，如图1所示。

图1 光栅尺5自由度动力学模型Fig.1 5−DOF Dynamic Model of Grating Ruler

其中，C点为光栅尺的质心，M、Iy、Iz分别为尺体质量、绕Y轴及绕Z轴的转动惯量。kx、cx为X方向的刚度和阻尼；ky1、kz1、cy1、cz1为安装点1处隔振器对应y方向与z方向的刚度和阻尼；ky2、kz2、cy2、cz2为安装点2处隔振器对应y方向与z方向的刚度和阻尼；qx、qy、qz分别为平台各方向对光栅尺的振动激励。l1、l2分别为光栅尺质心与安装点1，2的距离。显然，微幅振动时有：z1=z−l1θ；z2=z+l2θ；y1=y−l1φ；y2=y+l2φ则运动微分方程为：

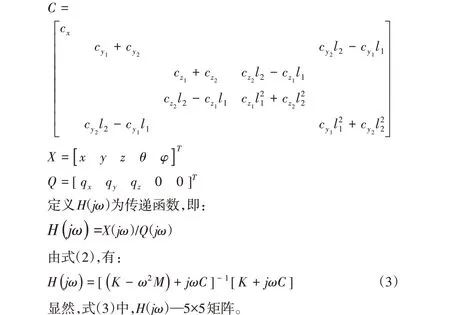
3 光栅尺动力学模型解耦与简化

考察式（2），y、z、θ、φ这4个自由度显然存在刚度耦合与阻尼耦合，有必要解耦上述动力学模型，以便简化隔振系统设计与分析过程。分析刚度矩阵K和阻尼矩阵C，若l1=l2，则矩阵K和C的非对角元素为零，实现了解耦。实际应用中，光栅尺尺体通常为均匀质量，长条状；即其质心与几何中心重合，位于两侧安装点连线中点，满足上述解耦条件。考虑实际的隔振系统设计中，通常取同一方向的隔振单元其刚度和阻尼参数为相同值，故定义式（2）光栅尺动力学模型相关参数如下：

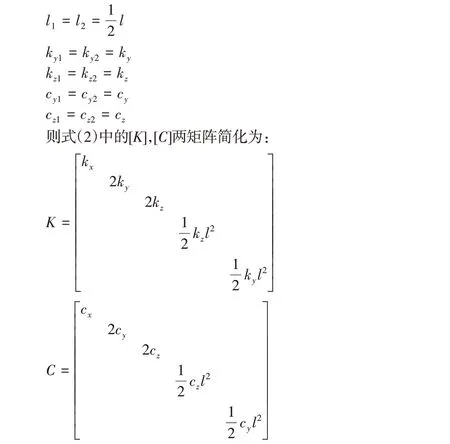
显然，光栅尺动力学模型式（2）实现解耦。由振型叠加原理[8]，可知，式（2）解耦后，该5自由度系统动力学模型可描述为各方向单自由度振动的叠加，即：

4 仿真与分析

根据上述动力学模型，在Matlab中建立了光栅尺5自由度隔振系统模型，分析其在安装基座激励下的振动响应特性。隔振系统各参数值，如表1所示。

表1 某光栅尺隔振系统参数Tab.1 Parameters of Vibration Isolation System for One Grating Ruler

切削加工时，引起机床振动的因素很多，主轴不平衡、机床运动部件安装误差、导轨磨损、非平稳切削等是较常见因素，某些工况下，不稳定的切削过程甚至可导致机床颤振。而机床加工过程中的各种振动均会通过安装位置传递给光栅尺，因此，机床的振动特性即光栅尺的振动激励特性。

由隔振原理，输入激励频率在共振峰 2 倍以上，则隔振系统可以有效隔离[11]。自由度频响特性值，包括固有频率、 2 倍频率点、对应隔振率及25Hz频率点隔振率，如表2所示。考察该表可知，该系统固有频率和 2 倍频率均较低。其中X、Y、Z三个平动自由度，固有频率均小于8.5Hz， 2 倍频率小于11.9Hz，对应的机床主轴转速分别为510rpm和714rpm。Ry，Rz两回转自由度固有频率分别为14.24Hz 和13.63Hz， 2 倍频率略高，分别为20.14 Hz和19.27Hz。

表2 各自由度频率响应特性Tab.2 Frequency Response Characteristics

数控机床工作时切削用量随工况变化范围较大，主轴转速与进给速度等参数变化的区间同样范围较大。但对于光栅尺精度较敏感的精加工而言，通常主轴转速设定较高，因此由于机床主轴旋转误差和颤振所引起的振动激励频率也较高。上述X，Y，Z平动自由度和Rx，Ry回转自由度的 2 倍频率点对应的主轴转速分别为714rpm 以下和1209rpm 以下，对光栅尺误差敏感的精加工较少工作于此转速范围。

光栅尺隔振系统各自由度的频率响应曲线，如图2、图3 所示。比较直观反映了激励频率在1000Hz以下的隔振效果，图中，横坐标为对数频率坐标（f∕Hz），纵坐标为位移放大系数（dB）。其中，图2为X、Y、Z方向平动自由度频率响应曲线，振动激励频率为25Hz时，对于光栅尺误差敏感方向X，隔振率为−11.9dB。Y，Z两平动自由度隔振率为−9.31dB。

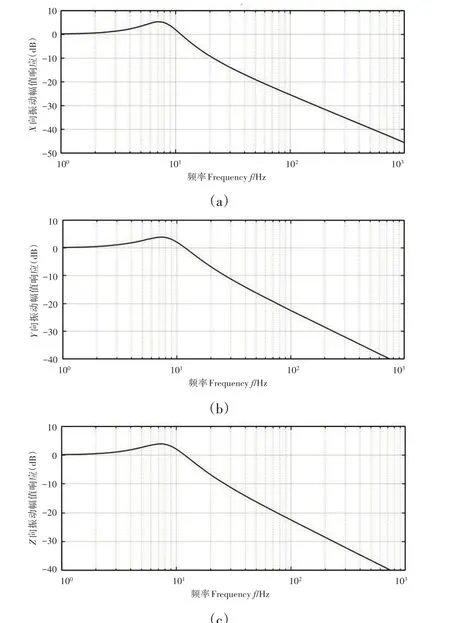
图2 光栅尺X、Y、Z平动自由度频响曲线Fig.2 X、Y、Z DOF Frequency Response Curve of Grating Ruler

光栅尺Ry、Rz两回转自由度频率响应曲线，如图3所示。Ry、Rz两回转自由度在25Hz激励频率的响应分别为−1.52dB、−1.99 dB。系统各自由度隔振效果随频率增加而愈加显著，在100 Hz处（对应机床主轴转速3000rpm），X、Y、Z方向平动自由度隔振率均已超过−23dB，Ry、Rz方向则超过−14dB。由于数控机床精加工时主轴转速较高，其振动激励频率通常更高，故本系统在高速切削工况下隔振效果良好。随着数控机床的高速化，其工作台各轴快速平移，急起、急停等已经成为常规工况，使得机床各运动部件具有较高加速度[7]。同时，加工过程中，刀具切入、切出时还会对机床形成突加载荷。

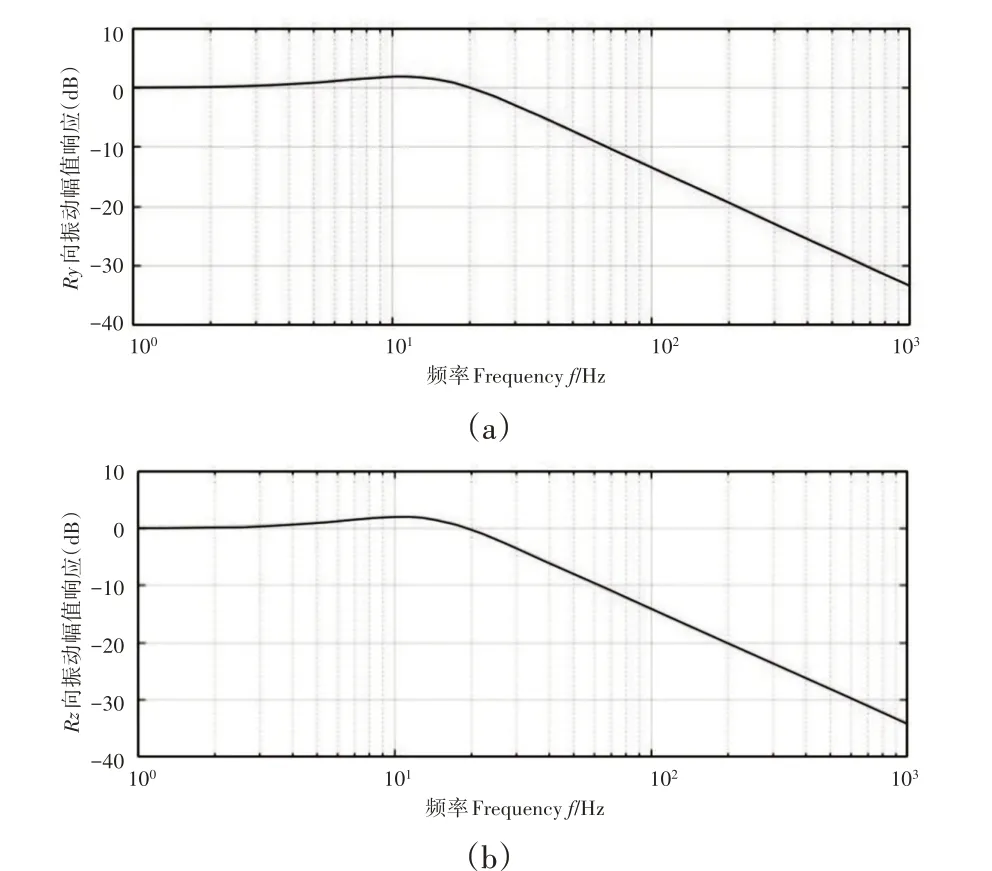
图3 光栅尺Ry、Rz转动自由度频响曲线Fig.3 Ry、Rz DOF Frequency Response Curve of Grating Ruler

由于各轴导轨安装间隙的存在，上述高加速度工况通常以冲击激励的形式作用于工作台等机床运动部件。以单位阶跃响应和单位冲击响应仿真光栅尺隔振系统在上述突加载荷与冲击工况下的稳定性。系统在阶跃和单位冲击下X方向和Ry方向的时域响应曲线，如图4、图5所示。

图4 X方向单位阶跃响应与冲击响应Fig.4 X Direction’s Step Response and Impact Response

由图4，系统在X方向的阶跃响应稳定时间为0.25s，峰值保持的时间<0.1s；单位冲击响应稳定时间为0.2s，峰值保持的时间<0.06s。由图5，Ry方向的阶跃响应稳定时间为0.08s，峰值保持的时间<0.05s；单位冲击响应稳定时间为0.18s，峰值保持的时间<0.05s。单位阶跃响应与单位冲击响应的仿真结果反映了光栅尺隔振系统稳定性较好，对突加载荷和冲击下所导致的扰动，能很快回复正常状态。因此，本隔振系统能更好适应高速数控机床愈加严苛的工况。

5 结论

在分析光栅尺结构特点的基础上，建立了光栅尺隔振系统5自由度动力学模型，并对动力学模型进行了解耦及隔振传递函数分析。对该隔振系统动力学模型仿真分析结果表明：

（1）建立了5自由度光栅尺动力学模型，该模型较好地体现了光栅尺的特征与工况。为光栅尺的隔振分析与隔振系统设计奠定理论基础，也为类似条状结构的动力学分析提供了参考。

（2）基于隔振对象结构特性进行的动力学模型解耦，可有效降低分析难度且不失准确性。

（3）依此方法，可易于计算隔振系统的各自由度固有频率，以便设计隔振系统时，为不同应用场合与工况，适时调整刚度、阻尼等隔振系统参数。

（4）合理设计隔振系统参数，使系统各阶固有频率的 2 倍频率均小于机床主要工况的激励频率，则可获得明显的隔振效果，更有利于光栅尺在颤振等工况下的测量精度保持。